基于达朗贝尔原理的废塑料薄膜耦合振动分选与参数优化设计

张启铄 张宗素 谢世龙 毛文杰 杨立勇 吴虎 杨先海

文章編号：1671-3559（2024）03-0376-07DOI：10.13349/j.cnki.jdxbn.20240312.001

摘要： 为了提高废塑料薄膜的回收效率和利用价值， 提出一种废塑料薄膜耦合振动分选方法； 基于达朗贝尔原理， 建立所提出方法的动力学方程， 分析分选效果的影响因素，确定分选效果的评价指标；确定废塑料薄膜耦合振动分选设备的优化设计变量，建立优化目标函数，编写优化程序，得到最优的废塑料薄膜耦合振动分选设备参数；研制废塑料薄膜耦合振动分选设备，对所建立动力学方程进行验证实验。结果表明：当振动床面振动角为48.63°，振动电机角速度为27.62π rad/s且振动床面横、 纵向倾角分别为9.41°、 12°时，分选效果最好；验证实验的结果与优化程序的结果相近，验证了所建立动力学方程的正确性；相对于传统的风力振动分选方法，所提出方法在相同分选时间内的分选距离增加18.66%，分选效果更好，验证了所提出方法的有效性。

关键词： 机械优化设计； 耦合振动分选； 达朗贝尔原理； 动力学分析； 废塑料薄膜； 正交实验

中图分类号： TH122

文献标志码： A

开放科学识别码（OSID码）：

Coupled Vibration Sorting of Waste Plastic Film Based on

DAlembert Principle and Parameter Optimization Design

ZHANG Qishuo1， ZHANG Zongsu1， XIE Shilong1， MAO Wenjie1， YANG Liyong2，

WU Hu1， YANG Xianhai1

（1. School of Mechanical Engineering， Shandong University of Technology， Zibo 255000， Shandong， China;

2. Shandong Wintech Technology Co.， Ltd.， Zibo 255130， Shandong， China）

Abstract： To improve recovery efficiency and utilization value of waste plastic film， a coupled vibration sorting method for waste plastic film was proposed. On the basis of dAlembert principle， kinetic equations of the proposed method was established to analyze influencing factors of sorting effects and determine evaluation indexes of sorting effects. Optimization design variables of waste plastic film coupled vibration sorting equipment were determined， an optimized objective function was established， and an optimization procedure was written to obtain the optimized parameters of the waste plastic film coupled vibratory sorting equipment. The waste plastic film coupled vibration sorting equipment was developed， and the proposed kinetic equations were verified. The results show that the best sorting effect is achieved when the vibration angle of vibration deck is 48.63°， the angular velocity of vibration motor is 27.62π rad/s， and the lateral and longitudinal inclination angles of vibration bed surface are respectively 9.41° and 12°. The results of the verification experiment are similar to those of the optimization procedure， which verifies correctness of the established kinetic equations. Compared with the traditional wind vibration sorting method， the proposed method increases the sorting distance by 18.66% in the same time， and the sorting effect is better， which verifies effectiveness of the proposed method.

Keywords： mechanical optimization design; coupled vibration sorting; dAlembert principle; kinetic analysis; waste plastic film; orthogonal experiment

收稿日期： 2023-03-24          网络首发时间：2024-03-12T20：12：25

基金项目： 国家自然科学基金项目（52075306）

第一作者简介： 张启铄（1998—），男，山东济宁人。硕士研究生，研究方向为机械优化设计。E-mail： zhangqishuo321@126.com。

通信作者简介： 杨先海（1963—），男，山东淄博人。教授，博士，博士生导师，研究方向为机构学创新设计。E-mail： yxh@sdut.edu.cn。

网络首发地址： https：//link.cnki.net/urlid/37.1378.N.20240312.1507.002

塑料薄膜常见于包装、 农业等领域，常见的材料有聚乙烯（PE）、 聚丙烯（PP）、 聚氯乙烯（PVC）、 聚对苯二甲酸乙二醇酯（PET），以及聚苯乙烯（PS）等。2021年全国塑料薄膜生产总量为16 087.1 kt［1］，這些薄膜在1 a内的废弃比例高达80%。目前对于废弃塑料薄膜的处理方法主要有填埋、 焚烧、 高温裂解、 再生造粒等［2］。填埋和焚烧对环境的污染较严重， 而高温裂解和再生造粒对薄膜的纯度要求较高，不同种类的塑料在熔化后的化学相容性低， 直接影响再生塑料的质量和性质， 因此为了高值化回收废塑料薄膜， 必须先进行分选， 提高废塑料薄膜的纯度［3］。

当前较常见的分选技术可以分为干法分选和湿法分选， 具体有人工分选、 近红外分选、 静电分选、 颜色分选、 气流分选、 密度分选， 以及浮力分选等。 Scott等［4-5］结合近红外光谱与神经网络提出了一种对不同塑料进行识别的方法， 该方法易于扩展到其他塑料的识别； Chen等［6］运用近红外光谱技术将塑料分类精度从75%提高到97%以上； Dodbiba等［7］将摩擦静电分离与空气沉积分离相结合开发了一种新装置， 废塑料薄膜的回收率可达92.5%以上； Bezati等［8-9］在塑料中添加示踪剂， 对塑料制品加以区分， 并测试了多种示踪剂的效果； 郭莹莹［10］研究水平风选机内部的流场并建立气固两相流的控制方程，并据此提出一种新型的柱式水平气流风选机模型；Yang等［11］研究旋风分离器的各项参数， 分析旋风分离器的分离原理并进行尺寸优化， 提高了分选效率。作为一种常见的送料方式， 振动送料也成为热门研究课题。 宋宏斌等［12-13］对振动卸料机进行研究， 建立空间振动卸料机的力学模型和数学模型并进行了求解。 随着振动送料理论的成熟， 振动分选理论被提出。 赵海星等［14-15］将风力分选与振动分选相结合， 提出风力振动复合分选技术， 设计分选样机， 并推导塑料薄膜在样机中的运动规律， 给出了塑料薄膜不同运动状态的参数条件； 为了提高废塑料薄膜的振动分选精度， Wang等［16］提出一种计算废塑料薄膜变形的虚拟质点法， 研究废塑料薄膜的变形规律， 为后续研究提供了一种准确、 快捷的分析方法。

上述研究对废塑料薄膜的分选都作出了重要贡献，许多研究成果已应用于现实生活，部分取代有损健康的人工分选劳动，提高了废塑料薄膜分选行业的生产效率；但是缺点也很明显，即依据上述研究设计的分选设备大多结构复杂，成本较高，维护不便，因此导致废塑料薄膜的自动分选设备难以全面取代人工劳动。本文中提出一种废塑料薄膜耦合振动分选方法（简称本文方法），基于达朗贝尔原理，建立本文方法的动力学方程，确定废塑料薄膜耦合振动分选设备的优化设计变量并建立优化目标函数，研制耦合振动分选设备，实验验证所建立动力学方程的正确性和本文方法的有效性。

1  本文方法

为了得到废塑料薄膜耦合振动分选效果较优的设计参数，首先建立本文方法的动力学方程，研究不同参数对分选效果的影响。

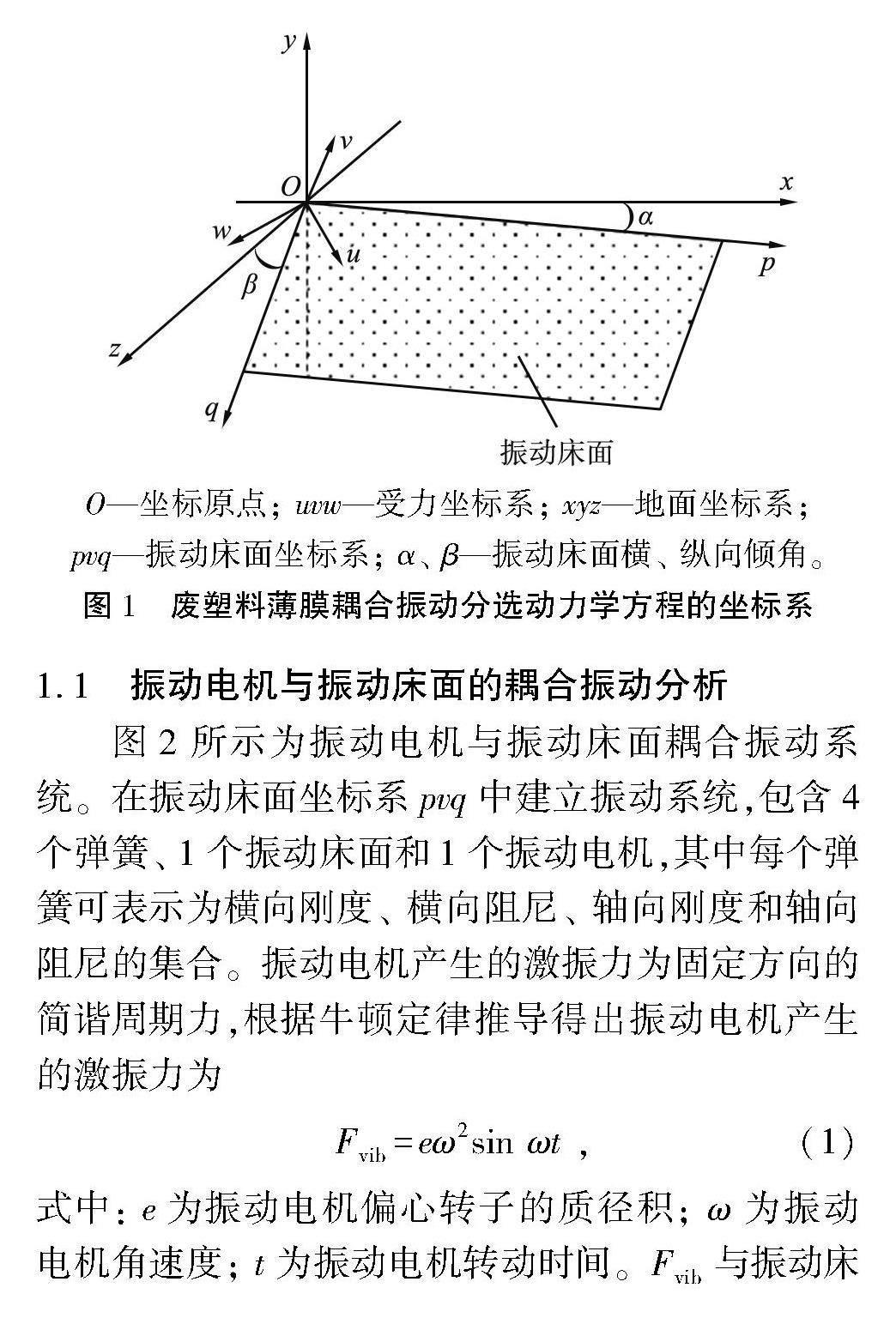
图1所示为废塑料薄膜耦合振动分选动力学方程的坐标系。分别建立地面坐标系xyz、 受力坐标系uvw以及振动床面坐标系pvq，其中地面坐标系固定不动，而受力坐标系和振动床面坐标系随振动床面角度的调节而变化。受力坐标系的u轴指向振动床面梯度下降的方向，v轴指向振动床面的法向，w轴分别与u、 v轴垂直，w轴始终与xOz水平面平行。振动床面与x、 z轴的夹角分别为振动床面横、 纵向倾角α、 β。

1.1  振动电机与振动床面的耦合振动分析

图2所示为振动电机与振动床面耦合振动系统。在振动床面坐标系pvq中建立振动系统，包含4个弹簧、 1个振动床面和1个振动电机，其中每个弹簧可表示为横向刚度、 横向阻尼、 轴向刚度和轴向阻尼的集合。振动电机产生的激振力为固定方向的简谐周期力，根据牛顿定律推导得出振动电机产生的激振力为

Fvib=eω2sin ωt ，（1）

式中： e为振动电机偏心转子的质径积； ω为振动电机角速度； t为振动电机转动时间。Fvib与振动床

面的夹角θ称为振动床面振动角， mb为振动床面质量。角度调节架等效为地面，振动床面由4个相同的弹簧并联在地面上， kt、 ka分别为弹簧横向、轴向刚度， ct、 ca分别为弹簧横向、 轴向阻尼。

根据达朗贝尔原理，建立振动电机与振动床面耦合振动系统的振动微分方程，即

mbv··b+ctv·b+ktvb=Fvibsin ωt cos θ ，

mbp··b+cap·b+kapb=Fvibsin ωt sin θ ，

（2）

式中： vb、 v·b、 v··b分别为振动床面在v方向的位移、 速度、 加速度； pb、 p·b、 p··b分别为振动床面在p方向的位移、 速度、 加速度。

对方程（2）进行求解，得到振动床面的稳态响应，即

pb（t）=Fvibcos θ（kt-mbω2）2+c2tω2cos

ωt-arctanctωkt-mbω2，

vb（t）=Fvibsin θ（ka-mbω2）2+c2aω2cos

ωt-arctancaωka-mbω2

。（3）

1.2  振动床面与废塑料薄膜的耦合振动分析

1.2.1  废塑料薄膜的受力分析

图3 所示为废塑料薄膜的受力分析。

振动床面在振动过程中带动振动床面附近的空气产生垂向流动，废塑料薄膜因质量较小且面积较大而极易受空气作用影响。当振动床面向下运动时，振动床面上方的空气也向下流动，废塑料薄膜在气流的作用下难以与振动床面分离，只会与振动床面间产生一个微小间隙。该间隙十分微小，而废塑料薄膜在v方向的速度较大，因此可以忽略间隙距离，有

vf=vb ，

v·f=v·b ，

v··f=v··b ，（4）

（a）uOv平面

（b）vOw平面

uvw—振動坐标系； O—坐标原点； Fn—振动床面对废塑料

薄膜的接触压力； Ff，u、 Ff，w—摩擦力在u、 w方向的分量；

Gu、 Gv—废塑料薄膜所受重力在u、 v方向的分量；

Fa—废塑料薄膜产生的气流作用力；

Fc—废塑料薄膜所受空气阻力。

图3  废塑料薄膜的受力分析

式中vf、 v·f、 v··f为废塑料薄膜在v方向的位移、 速度、 加速度。由此，废塑料薄膜产生的气流作用力Fa由废塑料薄膜在v方向的动力学公式反推计算得到，即

Fn-Fa=mv··b+Fc+Gv ，（5）

式中： Fn为振动床面对废塑料薄膜的接触压力， Fn-Fa<0时Fn=0， Fn-Fa>0时Fa=0； Fc为废塑料薄膜所受空气阻力； Gv为废塑料薄膜所受重力在v方向的分量。

Fc的计算公式［17］为

Fc=12CρAv·2f，  v·f>0 ，

0，v·f≤0 ，（6）

式中： C为空气阻力系数，与迎风面形状有关，迎风面为平板形时通常取为1； ρ为空气密度，通常取为1.293 g/L； A为迎风面积。当v·f≤0时，废塑料薄膜不受空气阻力的作用，Fc=0。

1.2.2  本文方法的动力学方程建立

对于运动过程中的任一时刻，根据达朗贝尔原理，建立本文方法的动力学方程为

mu··f=Gu-Ff，u ，

v··f=v··b ，

mw··f=-Ff，w ，（7）

式中： u··f、 w··f分别为废塑料薄膜在u、 w方向的加速度； Gu为废塑料薄膜所受重力在u方向的分量； Ff，u、 Ff，w分别为摩擦力在u、 w方向的分量。

对于一般动力学问题，分析摩擦力时常采用库仑摩擦模型［18］进行求解。当2个物体的相对速度和相对切向加速度均为0时，接触点处于静摩擦状态，此时摩擦力的取值是一个范围，具体取值取决于外力的大小。

摩擦力的方向与摩擦状态有关： 当2个物体处于动摩擦状态时， 摩擦力的方向指向相对运动方向的反方向； 而当处于静摩擦状态时， 摩擦力为驱动力，与其他力的合力指向物体加速度的方向。 根据摩擦力的影响规律， 结合牛顿第二、 第三定律， 推导废塑料薄膜在动、 静摩擦状态下所受的摩擦力分别为

Ffk=μFn ，

Ffk，u=-u·r1/（u·2r+w·2r）Ffk ，

Ffk，w=-w·r1/（u·2r+w·2r）Ffk ，（8）

Ffs，u=mu··f-Gu ，

Ffs，w=mw··f ，

Ffs=F2fsu+F2fsw ，（9）

式中： Ffk为动摩擦力， Ffk，u、 Ffk，w分别为动摩擦力在u、 w方向的分力； Ffs为静摩擦力； Ffs，u、 Ffs，w分别为静摩擦力在u、 w方向的分力；u·r=u·f-v·b为废塑料薄膜在u方向相对于振动床面运动的速度，其中u·f、 u·b分别为废塑料薄膜、 振动床面在u方向的速度； w·r=w·f-w·b为废塑料薄膜在w方向相对于振动床面运动的速度，其中w·f、 w·b分别为废塑料薄膜、振动床面在w方向的速度。

求得任一时刻u、 w方向的摩擦力后，代入式（7），即可得到废塑料薄膜在该时刻的加速度。

1.2.3  本文方法的动力学方程求解

废塑料薄膜在运动过程中的摩擦状态不断变化，在计算过程中无法恒定地使用式（8）或式（9）进行摩擦力求解，使得所建立动力学方程（7）的解析解难以给出，因此使用计算机进行数值求解成为最佳选择。

将求解时间段划分为若干微元时间Δt，并给出u、 w方向的位移和速度初始条件：

u（0）=u0， u·（0）=u·0 ，

w（0）=w0， w·（0）=w·0 。（10）

在微元时间内进行所建立动力学方程的求解，解出该微元时间废塑料薄膜在u、 w方向的末位移和末速度作为下次计算的初始条件，如此循环即可完成整个设定时间段的计算。使用数值方法求解，可以实时计算摩擦状态并根据摩擦状态选择式（8）或式（9）进行摩擦力求解。

2  废塑料薄膜耦合振动分选设备参数优化设计

2.1  优化设计变量的确定

对单一废塑料薄膜的轨迹进行求解后，代入不同废塑料薄膜的摩擦系数μ和密度等参数，即可得到该废塑料薄膜的末位置S。对2种不同的废塑料薄膜进行求解，得到每种废塑料薄膜的末位置，分别记为S1和S2。每种废塑料薄膜的末位置Sk （k=1， 2， …， n， n为正整数）可在振动床面坐标系pvq中沿p、 q轴分解为Skp、 Skq，分别表示废塑料薄膜末位置的p、 q坐标。令S1p=S2p=Sp，求解此时的ΔSq=S1q-S2q。当振动床面p方向长度为Sp时，2个废塑料薄膜滑落的q方向位移差为ΔSq，即分选距离。分选距离ΔSq越大，则分选效果越好。

根据式（7）可知，直接影响废塑料薄膜运动的作用力为重力在u方向的分量和摩擦力。重力在u方向的分量受振动床面倾斜角度的影响，而振动床面倾斜角度由α、 β共同决定。

影响摩擦力的因素较复杂，首先需要确定摩擦力的状态，再根据式（8）、 （9）确定摩擦力。废塑料薄膜所受摩擦力与Fn、 μ有关，还与废塑料薄膜和振动床面间的相对运动状态有关。结合式（4）、 （5）、 （6）可知，Fn主要受振动床面v方向加速度的影响。由此可知，摩擦力的影响因素主要是μ和振动床面运动状态，而振动床面运动状态即为式（3）中的振动床面稳态响应，影响因素包括Fvib、 θ、 ω、 mb、 kt、 ka、 ct、 ca。同时，振动床面的p方向长度Xp限制了废塑料薄膜的p方向位移。由此可知，废塑料薄膜分选效果的影响因素即为α、 β、 μ、 e、 θ、 ω、 mb、 kt、 ka、 ct、 ca、 Xp。

2.2  优化目标函数的建立

根据确定的优化设计变量， 研制废塑料薄膜耦合振动分选设备， 实物图如图4所示， 其中振动床面用于分选废塑料薄膜， 侧挡板用于防止废塑料薄膜过早滑落， 控制箱用于控制ω、 α、 β的中枢。 该设备通过电动推杆的伸缩调节α、 β， 通过振动电机调速器调节ω， 通过连接振动电机的振角调节器调节θ。

表1所示为废塑料薄膜耦合振动分选设备参数，其中仅θ、 ω、 α、 β为可调节的参数。由于Xp、 振动床面的q方向长度Xq、 kt、 ka、 ct、 ca、 mb、 e都是设备中不可调节的参数， 因此均不作为优化设计变量。

将动力学分析流程编写为MATLAB函数，记作ΔSq（θ， ω， α， β）。以分选距离ΔSq最大化为优化目标，以实验平台的各参数可调范围为约束条件，建立优化目标函数为

min -ΔSq（θ， ω， α， β） ，（11）

满足0°≤θ≤90° ， 0≤ω≤100π ， 0°≤α≤12° ， 0°≤β≤12° 。

利用MATLAB软件编写优化程序，对优化目标函数（11）进行计算，得到耦合振动分选设备的参数优化设计结果，如表2所示。

3  实验验证

3.1  实验参数设置

利用正交实验法研究θ、 ω、 α、 β对分选距离的影响。影响分选距离的可变参数个数为4，因此采用四因素三水平的正交实验。按照等间距原则，各变量在调节范围内均匀取值，废塑料薄膜耦合振动分选正交实验的因素水平如表3所示。表4所示

为废塑料薄膜耦合振动分选正交实验的分组。

待分选的廢塑料薄膜材料使用生活中常见的PVC和PP，长度、 宽度、 厚度均为60、 60、 0.3 mm， 密度分别为1 380、 900 kg/m3，摩擦系分别为0.5、0.2。 由于动、 静摩擦系数相近， 因此统一取值进行近似处理。 每组实验的参数设置过程如下： 1）计算α、 β对应的电动推杆伸长量； 2）控制步进电机， 将电动推杆伸长到相应位置， 调节α、 β； 3）拨动振动角调节杆， 通过控制振动角调节杆伸长和缩短对θ进行调节； 4）通过电机调速器旋钮将ω调节到实验值； 5）电机通电， 振动床面振动； 6）振动床面振动达到稳态后， 将废塑料薄膜平稳放置在振动床面的初始点位； 7）废塑料薄膜滑落后， 记录落点的位置。

3.2  实验结果与分析

表5所示为废塑料薄膜耦合振动分选正交实验的结果。从表中可以看出，当θ=60°， ω=33π rad/s，α=8°， β=12°时， 第4组废塑料薄膜的分选距离最大。 为了进一步细化数据， 再进行一次细化的正交实验， 在第4组参数的附近取值， 表6所示为细化正交实验的因素水平。 重复上述实验步骤， 记录细化正交实验的结果， 如表7所示。 由表可知， 细化正交实验所得的最佳参数组合为第4组， 即θ=50°，ω=27π rad/s， α=9°， β=12°， 此时废塑料薄膜的分选距离最大， 为478.3 mm。 此结果与表2中的参数优化设计结果相近， 验证了所建立的本文方法的动力学方程的正确性和参数优化设计结果的正确性。

3.3  本文方法的有效性验证

传统的风力振动分选方法［19］优化设计后所得PVC薄膜的平均推进速度为15.63 mm/s，PP薄膜的

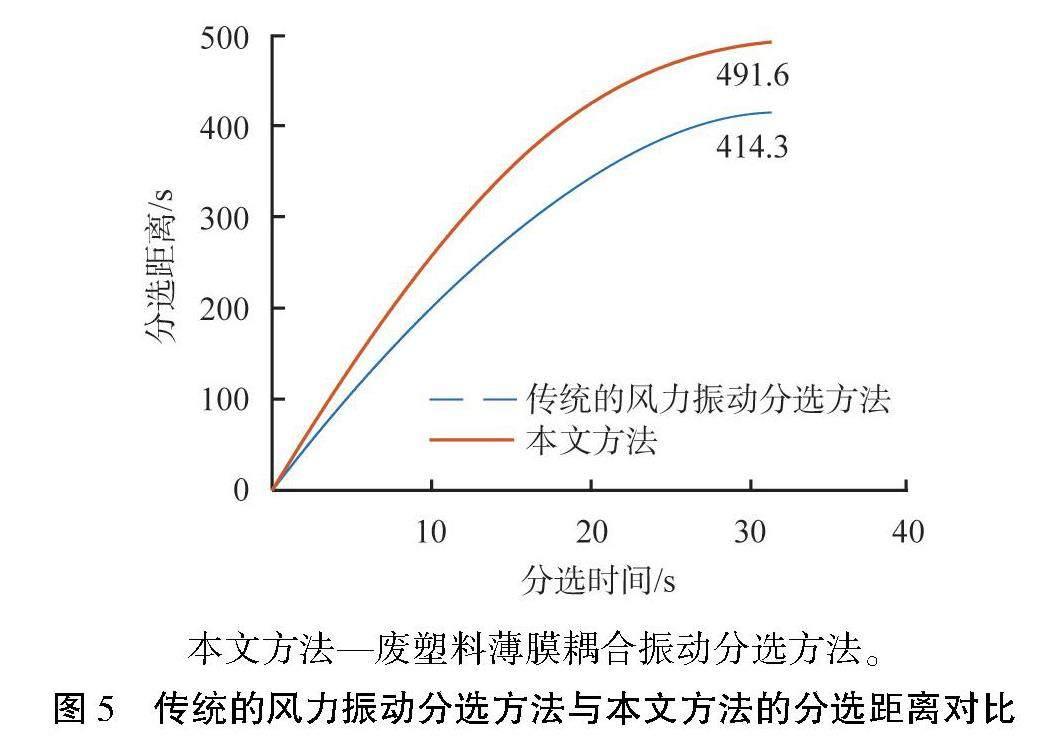
平均推进速度为28.85 mm/s，两者之差13.22 mm/s即为平均分选速度。利用本文方法进行分选，分选时间为31.34 s。在相同分选时间内对比2种方法的分选距离，结果如图5所示。由图可知，在相同分选时间内，本文方法的分选距离为491.6 mm，传统的风力振动分选方法的分选距离为414.3 mm，相对于传统的风力振动分选方法，本文方法的分选距离增加18.66%，分选效果更好。

本文方法—废塑料薄膜耦合振动分选方法。

图5  传统的风力振动分选方法与本文方法的分选距离对比

4  结论

本文中提出了一种废塑料薄膜耦合振动分选方法，基于达朗贝尔原理，建立本文方法的动力学方程，分析分选效果的评价指标；通过确定优化设计变量和建立优化目标函数，研制废塑料薄膜耦合振动分选设备并进行实验验证，得到以下主要结论：

1）当振动床面振动角为48.63°，振动电机角速度为 27.62π rad/s，振动床面横、 纵向倾角分别为9.41°、 12°时，废塑料薄膜的分选距离最大，分选效果最好。

2）采用正交实验法设计的验证实验结果与理论计算结果相近，验证了所建立本文方法的动力学方程的正确性。

3）与传统的风力振动分选方法对比，本文方法在相同分选时间内的分选距离增加了18.66%，分选效果更好，验证了本文方法的有效性。

参考文献：

［1］  马占峰， 牛国强， 芦珊. 中国塑料加工业（2021）［J］. 中国塑料， 2022， 36（6）： 142.

［2］  刘程锦， 缪畅， 肖围， 等. 农用塑料薄膜的资源化回收利用进展［J］. 应用化工， 2020， 49（增刊2）： 213.

［3］  李晓， 崔燕， 刘强， 等. 我国废塑料回收行业现状浅析［J］. 中国资源综合利用， 2018， 36（12）： 99.

［4］  SCOTT D M， WATERLAND R L. Indentification of plastic waste using spectroscopy and neural networks［J］. Polymer Engineering & Science， 1995， 35（12）： 1011.

［5］  SCOTT D M. A two-colour near-infrared sensor for sorting recycled plastic waste［J］. Measurement Science and Technology， 1995， 6（2）： 156.

［6］  CHEN X Z， KROELL N， DIETL T， et al. Influence of long-term natural degradation processes on near-infrared spectra and sorting of post-consumer plastics［J］. Waste Management， 2021， 136： 213.

［7］  DODBIBA G， SHIBAYAMA A， SADAKI J， et al. Combination of triboelectrostatic separation and air tabling for sorting plastics from a multi-component plastic mixture［J］. Materials Transactions， 2003， 44（12）： 2427.

［8］  BEZATI F， FROELICH D， MASSARDIER V， et al. Addition of X-ray fluorescent tracers into polymers， new technology for automatic sorting of plastics： proposal for selecting some relevant tracers［J］. Resources， Conservation & Recycling， 2011， 55（12）： 1214.

［9］  BEZATI F， FROELICH D， MASSARDIER V， et al. Addition of tracers into the polypropylene in view of automatic sorting of plastic wastes using X-ray fluorescence spectrometry［J］. Waste Management， 2010， 30（4）： 591.

［10］  郭莹莹. 圆柱卧式垃圾风力分选机内部流场的数值模拟研究［D］. 辽宁： 辽宁工程技术大学， 2014： 1-7.

［11］  YANG X H， LIU X， SONG L P， et al. Study on the separators for plastic wastes processing［J］. Procedia Engineering， 2017， 174： 497.

［12］  宋宏斌. 空间振动卸料机的振动强度［J］. 山东建材学院学报， 1995， 9（4）： 37.

［13］  宋宏斌， 岳振星. 空间振动卸料机的力学分析［J］. 山东建材学院学报， 1995， 9（1）： 73.

［14］  赵海星， 杨先海， 李玉君， 等. 软包装塑料振动分选机筛面运动参数优化［J］. 山东理工大学学报（自然科学版）， 2010， 24（5）： 67.

［15］  赵海星. 软包装废塑料复合分选技术和设备研究［D］. 淄博： 山东理工大学， 2010.

［16］  WANG T， LI Y B， YANG X H， et al. Study on flexible deformationofwasteplasticfilmbyfictitiousparticle method［J］. Environmental Technology & Innovation， 2021， 24： 101817.

［17］  蔡云濤. 轻质物料筛分空气阻力的数值模拟研究［D］.秦皇岛： 燕山大学， 2021： 11.

［18］  王晓军. Coulomb干摩擦模型与LuGre摩擦模型的分析与比较［J］. 常州工学院学报， 2017， 30（6）： 22.

［19］  李倩. 废塑料薄膜风力振动分选技术及设备研究［D］. 淄博： 山东理工大学， 2015： 43-45.

（责任编辑：王  耘）