基于机器学习的沥青路面压实度质量评估

赵琪 张健 张智民 陈镇文 刘泽佳 周立成 刘逸平

文章编号：1671-3559（2024）03-0331-10DOI：10.13349/j.cnki.jdxbn.20240318.001

摘要： 为了提高沥青路面压实度预测的准确率，基于机器学习对沥青路面进行压实度质量评估；通过对比实际工程中不同压路机在沥青路面上的振动规律，构建振动压路机-沥青路面系统动力学模型，利用Simulink数值仿真软件对所构建的模型进行仿真，设计8种工况，对比压实度计值、 压实度控制值、 机械驱动功率、滚轮综合刚度、 填筑体能量、 单位体积压实功率6个压实度质量评估指标在各工况下的适用性差异；采用支持向量机、 逻辑回归、 k最近邻、 决策树、 朴素贝叶斯法5种传统的机器学习方法对各工况下的压实度质量评估指标样本进行训练，对比压实度预测准确率；设计压路机在不同碾压次数时的碾压路线，对比分别采用最优压实度质量评估指标和单一压实度质量评估指标的压实度预测准确率。结果表明：不同压实度质量评估指标在不同工况下的适用性不同，即使在同一种工况下，不同碾压次数时的适用性也存在差异；采用最优压实度质量评估指标代替单一压实度质量评估指标，压实度预测准确率提高5.8%； 在5种传統的机器学习方法中，朴素贝叶斯法预测最优压实度质量评估指标类型的准确率最高，为96.22%。

关键词： 沥青路面； 压实度质量评估； 机器学习； 压实度； 动力学模型

中图分类号： U416.217

文献标志码： A

开放科学识别码（OSID码）：

Quality Evaluation on Compaction of

Asphalt Pavements Based on Machine Learning

ZHAO Qi1， ZHANG Jian2， ZHANG Zhimin2， CHEN Zhenwen2， LIU Zejia1， ZHOU Licheng1， LIU Yiping1

（1. School of Civil Engineering and Transportation， South China University of Technology， Guangzhou 510641， Guangdong， China;

2. Guangzhou Chengtou Road and Bridge Engineering Co.， Ltd.， Guangzhou 510199， Guangdong， China）

Abstract： To improve accuracy of asphalt pavement compaction prediction， quality evaluation on compaction asphalt pavements was conducted on the basis of machine learning. By comparing vibration patterns of different rollers on asphalt pavements in practical engineering， a dynamical model of vibration roller-asphalt pavement system was constructed.  The constructed model was simulated by using Simulink numerical simulation software， and eight working conditions were designed to compare applicability differences of six quality evaluation indicators of compaction under different working conditions including compaction meter value， compaction control value， machine drive power， roller-integrated stiffness， filling energy， and unit volume compaction power. Five traditional machine learning methods， namely support vector machine， logistic regression， k-nearest neighbor， decision tree， and naive Bayes， were used to train quality evaluation indicator samples of compaction under different working conditions， and prediction accuracy of compaction was compared. Rolling routes of the roller with different rolling times were designed to compare predict accuracies of compaction using the

收稿日期： 2023-03-14          网络首发时间：2024-03-19T16：00：19

基金项目： 国家自然科学基金项目（11972162）；广东省自然科学基金项目（2023A1515012942）

第一作者简介： 赵琪（1998—），男，满族，吉林四平人。硕士研究生，研究方向为沥青路面压实度的智能监测。E-mail： 3487554692@qq.com。

通信作者简介： 刘泽佳（1975—），男，山东平度人。副教授，博士，硕士生导师，研究方向为固体力学。E-mail： zjliu@scut.edu.cn。

網络首发地址： https：//link.cnki.net/urlid/37.1378.N.20240318.1842.002

optimal quality evaluation indicators of compaction and the single quality evaluation indicators of compaction. The results show that the applicability of different quality evaluation indicators of compaction is different under each working condition. Even under the same working condition， the applicability with different rolling times is also different. Using the optimal quality evaluation indicators of compaction to evaluate indicators instead of the single quality evaluation indicators of compaction， the prediction accuracy of compaction is increased by 5.8%. Among the five traditional machine learning methods， naive Bayes method has the highest accuracy of predicting types of the optimal compaction quality evaluation indicators， which is 96.22%.

Keywords： asphalt pavement; quality evaluation on compaction; machine learning; compaction; dynamical model

沥青路面施工工期较短，平整度好，行车舒适性好且噪声小，同时养护方便。在沥青路面建设施工过程中，压实是沥青路面施工过程中的最后一道工序，压实度是压实过程中严格控制的指标之一［1］。压实度对沥青路面施工质量、 使用性能和使用寿命都有重要影响，在一定程度上决定了沥青路面的抗水损害能力、 抗车辙能力和耐久性，因此压实度质量评估被高度重视。

传统的检测压实度的方法一般有灌砂法、 钻芯取样法等［2］。这些方法存在很多不足之处，例如：利用灌砂法和钻芯取样法进行压实度的测定时，通常是对某个点进行检测的，随机性大，以点盖面的做法缺乏代表性；检测的结果具有滞后性，无法实时得到准确的压实度测量结果，最终导致人力、 物力、 财力浪费；传统的检测压实度的方法是有损的，对道路会造成一定程度的破坏。

由于传统压实检测技术存在诸多缺点，因此智能压实检测技术应运而生［3］。智能压实检测技术是采用计算机技术、高精密传感技术以及定位技术等高新技术集成的新型压实检测技术［4］。智能压实检测技术对于解决上述压实质量控制的不足具有非常显著的优势，但是目前在智能压实检测领域，仍有一些问题需要解决： 1）大多数智能压实检测设备仍基于碾压次数或单一压实度质量评估指标（简称单一指标）评价压实度。基于碾压次数的方法忽略了其他因素，具有较大误差，不宜采用；由于不同指标适用的工况不同，因此基于单一指标的方法对所有压实工况均采用单一指标时也会产生较大误差，甚至是错误的预测结论。 2）利用机器学习方法预测压实度的方法改进了传统方法的不足之处，但是需要进行大量的现场施工试验从而建立数据库，此过程需要耗费大量的人力和物力。

为了提高压实度预测准确率， 本文中对不同压实度质量评估指标在不同工况下的适用性进行探讨， 并结合相应工况选取最优压实度质量评估指标（简称最优指标）， 构建振动压路机-沥青路面系统动力学模型（简称本文模型）， 结合MATLAB/Simulink软件与机器学习， 对本文模型进行仿真， 设计8种不同类型的工况， 分别比较采用最优指标预测和采用单一指标预测压实度的准确率， 并结合路基压实现场试验， 进一步验证最优指标预测相对于单一指标预测的优势。

济南大学学报（自然科学版）第38卷

第3期赵琪，等：基于机器学习的沥青路面压实度质量评估

1  模型构建

1.1  智能压实检测技术

智能压实检测技术是用于土壤、 骨料和沥青混合料压实检测的技术。该技术通过测量压路机振动轮的加速度信号，计算得到相应的压实度质量评估指标，以此反映填筑体的压实程度［5］，因此构建振动加速度与压实度的关系模型尤为重要。智能压实检测技术工作原理如图1所示。加速度传感器竖直置于振动轮中轴，以测量振动轮的加速度信号。随着填筑体压实度的增加，振动轮所受地面的反作用力相应增加，加速度也增加。将所测加速度信号上传至位于驾驶室内的控制系统，从而计算相应的智能压实测试值，最终得到实时预测的压实度。根据智能压实检测技术工作原理，可以通过测量加速度信号评估填筑体的压实状态。

1.2  压实度质量评估指标

仅采用加速度评价压实度因所考虑影响因素有限，通常产生较大误差。为了有效地提高预测准确率，在加速度的基础上对压实度质量评估指标进行改进。指标的可靠性是直接影响智能压实检测技术适用性的关键因素。

压实度质量评估指标最早出现于20世纪70年代，即基于对加速度信号进行傅里叶变换后，加速度频域上2次谐波幅值与基频幅值之比与压实度之间的关系，以压实度计值（compaction meter value， CMV）作為压实度质量评估指标，记为vcm。其他频域上的振幅也对压实度产生一定的影响，因此更多频谱成分被引入畸变程度的计算中，以压实度控制值（compaction control value， CCV）作为压实度质量评估指标，记为vcc［6］。vcc是vcm的扩展，不仅考虑了振动轮垂直加速度在频域上的1、 2次谐波振幅，同时考虑了能够反映谐波形状的0.5、 1.5、 2.5、 3次谐波振幅。

Rinehart等［7］通过建立压实度和压路机消耗能量的关系式，提出以机械驱动功率（machine drive power）作为压实度质量评估指标，记为Pmd，计算式［7］为

Pmd=P-Wvsin α+z··g-（vl1+l2） ，（1）

式中： P为压路机总驱动功率； W为压路机重力； v为压路机行驶速度； α为压路机的爬坡角； z··为振动轮振动加速度；g为重力加速度； l1、 l2为机械自身能量损耗率。

Anderegg等［8］从振动力学的角度出发，通过求解二自由度动力学模型的二阶微分运动方程，提出以滚轮综合刚度（roller-integrated stiffness）作为压实度质量评估指标，记为ks，计算式［8］为

ks=Ω2m2+m0e0cos z

，（2）

式中： Ω为压路机激振频率； m2为振动轮质量； m0为振动轮中偏心块质量； e0为振动轮中偏心块的偏心距； 为偏心力与振动轮位移之间的相位滞后角； z为振动轮位移。

Krber等［9］采用作用力与位移的乘积表征能量，将2个连续的振动周期内的抵抗力和振动轮位移的时间历程进行积分，得到传递到填筑体的能量，提出以填筑体能量作为压实度质量评估指标，记为ω，计算式［9］为

ω=∫2T［-m1z··+（m1+m2）g+m0e0Ω2］z·dt ，（3）

式中： m1为机架质量； z·为振动轮振动速度； t为振动轮激振时间； T为振动轮激振周期。

Liu等［10］从压路机做功的角度出发，提出以单位体积压实功率作为压实度质量评估指标，记为Pvol，计算式［10］为

Pvol=2AQ+πF04ΩNbhv ，（4）

式中： A为振动轮振幅； Q为振动轮竖向荷载； F0为振动轮激振力； N为振动轮碾压次数； b为振动轮宽度； h为碾压层厚度。

目前，国内外已有10余种压实度质量评估指标应用于实际工程，其中vcm、 vcc、 Pmd、 ks、 ω、 Pvol这6个压实度质量评估指标应用效果较好，但是各指标在不同工况下的适用性和敏感性方面的研究还有所欠缺［11］。本文中对6个压实度质量评估指标在不同工况的适用性进行进一步研究，从而实现提高压实度预测准确率的最终目标。

1.3  本文模型及其动力学方程

路基的压实工艺分为初压、 复压和终压3个阶段，而振动压实主要集中在复压阶段，这也是本文中的重点研究阶段。目前已有学者针对不同类型的振动压路机提出相应的数学模型［12］，本文中通过对比实际工程中不同压路机在沥青路面上的振动规律，构建本文模型，如图2所示。

m1—机架质量； m2—振动轮质量； m3—随振沥青质量；

k1、 c1—减震器刚度、 阻尼； k2、 c2—沥青刚度、 阻尼；

F0—振动轮激振力； ω0—振动轮激振角频率；

t—振动轮激振时间； x1、 x2、 x3—m1、 m2、 m3的自由度；

Fs—地面的抵抗力。

本文模型的构建基于以下假设： 1）只考虑竖直方向的振动，本文模型的上半部分代表压路机的特性，下半部分代表沥青材料的特性； 2）将压路机的机架、 振动轮设为一定质量的刚体，并且机架与振动轮之间用无质量的弹簧-阻尼单元作为减震系统进行连接； 3）振动轮与地面之间紧密接触，不存在跳振，即x1=x2，其中x1、 x2分别为m1、 m2的自由度。根据牛顿第二定律，本文模型的动力学方程为

m1x··1+c1x·1+k1x1-c1x·2-k1x2=0 ，

（m2+m3）x··2+（c1+c2）x·+（k1+k2）x2-c1x·1-

k1x1=F0sinω0t ，

F0=m0e0ω20 ，（5）

式中： m3为随振沥青质量； k1、 c1分别为减震器刚度、 阻尼； k2、 c2分别为沥青刚度、 阻尼； ω0为振动轮的激振角频率。式（5）的矩阵形式为

MX··+CX·+KX=F（t） ，（6）

式中：M=m10

0m2+m3为质量矩阵； C=

c1-c1

-c1c1+c2为阻尼矩阵； K=k1-k1

-k1k1+k2为刚度矩阵； X、 X·、 X··分别为自由度位移、 速度、 加速度向量；

F（t）为激振力矩阵。

2  模型仿真

2.1  状态空间仿真

采用MATLAB/Simulink软件对本文模型进行机械振动分析仿真，较常用的方法有积分模块仿真、 状态空间仿真、 S函数模块仿真3种方法［13］。由于状态空间仿真有诸多优点，如仿真过程简单、 可读性好、 容易

操作等，因此本文中采用该方法进行仿真。

状态空间仿真采用状态方程模块State-Space，输入为正弦信号，输出为位移、 速度和加速度信号，并引入对信号进行快速傅里叶变换的Discrete模块，从而有利于根据加速度时域信号求解vcm、 vcc， ΔuΔt为计算输入对时间的变化率的微分模块。为了便于观察和分析，将仿真结果输出至Workspace工作空间。本文模型仿真过程如图3所示。

State-Space模块—状态方程模块；

Discrete模块—对信号进行快速傅里叶变换的模块；

ΔuΔt模块—计算输入对时间的变化率的微分模块。

2.2  仿真参数设置

在本文模型仿真的过程中，需要对各模块以及仿真参数进行设置。参考文献［14］设置本文模型的仿真参数，如表1所示，其中m3设置为m2的30%［15］。

设置2种振幅分别为0.25、 1.00 mm的信号波作为输入，本文模型中振动轮的加速度-时间曲线仿真结果如图4所示。由图可知，输出的2个振动轮加速度信号稳定并且大致符合振幅的倍数关系，可以初步验证仿真结果的可靠性。

2.3  工况设置

根据文献［16］， k1、 c1根据相应压路机说明书确定范围， k2、 c2根据沥青材料级配确定范围，并在此范围内梯度设置k2的数值。本文模型仿真参数值设置完成后，设置正弦波信号幅值和频率，输入仿真参数值并运行即可得到振动轮的加速度。再根据AC-25型沥青路面压实度-振动加速度-温度关系拟合结果［14］计算沥青路面压实度，即

振动压路机-沥青路面系统动力学模型中

振动轮的加速度-时间曲线仿真结果

K=0.826exp（0.009θ）z··-0.555θ+60.934

，（7）

式中： K为沥青路面压实度； θ为沥青路面摄氏温度。

通过给定温度值得到相应的压实度值， 再结合压路机的机械参数得到不同的压实度质量评估指标值， 并通过计算不同工况下压实度质量评估指标值与压实度值之间的相关系数得到不同工况下的最优指标。 在此过程中， 根据正弦波信号振幅的不同， 将工况设置为低、 高幅2种， 振幅分别为1、 2  mm； 将频率设置为低、 高频2种，频率分别位30、 50 Hz；将温度设置为低、 高温2种，温度分别为120、 150 ℃。将以上3种物理参数结合形成8种工况：低温低频低幅、 高温低频低幅、 低温低频高幅、 低温高频低幅、 低温高频高幅、 高温低频高幅、 高温高频低幅、 高温高频高幅，分别记为工况1、 2、 …、 8。通过梯度改变k2值，从而形成320個样本。

2.4  仿真结果分析

8种工况下压实度与vcm、 vcc、 Pmd、 ks、 ω、 Pvol这6个压实度质量评估指标之间的关系如图5所示。由图可知：在工况1下，vcm、 vcc指标曲线突升和突降较明显，与压实度的相关性较差，而另外4种指标和压实度的相关性较好；在工况7下， ω、 Pmd指标曲线在后期有突升和突降，而vcm、 vcc曲线相对平滑。由此可知，不同工况下，不同指标与压实度的相关性不同，如果用不同工况下最优指标评价压实度，将能提升预测准确率。

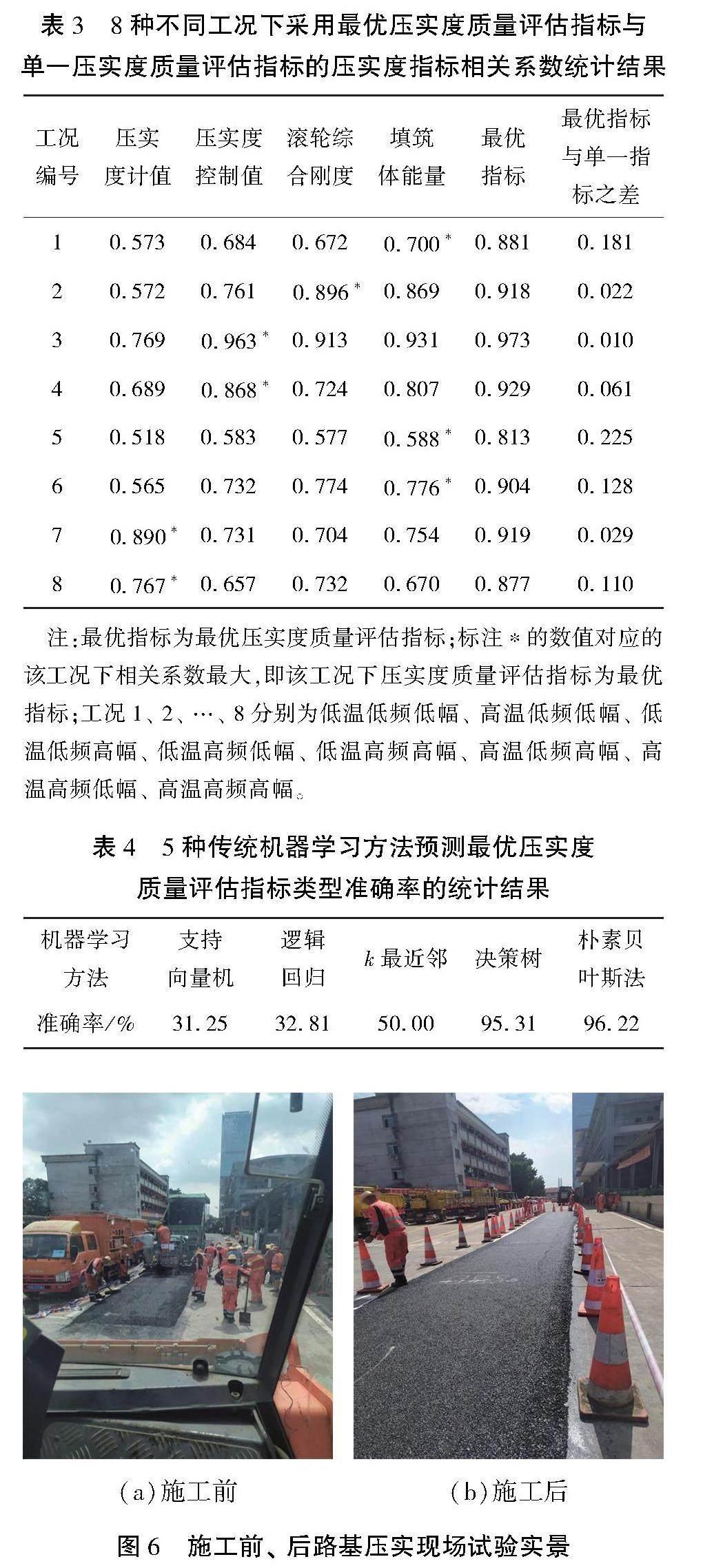
对不同指标和压实度之间的相关性进行数值分析， 根据碾压次数的不同， 将工况分为4个阶段， 并且统计不同阶段时不同指标与压实度的相关系数ρ。ρ的绝对值越接近1， 说明指标与压实度之间的相关性越强， 越适宜作为评价此工况下压实度的最优指标。 在统计过程中发现： 3个能量类的指标中， ω与压实度的ρ大于另外2个指标，因此将ω代表能量类指标参与对比分析。统计8种工况下不同压实度质量评估指标与压实度的ρ，结果如表2所示。标注*的数值对应的该工况下ρ最大，即该工况下压实度质量评估指标为最优指标。由图可知，最优指标分布没有规律，进一步验证了不同工况下不同指标与压实度的相关性不同的结论。

统计8种工况下采用最优指标与单一指标的相关系数ρ，针对不同工况下4种碾压次数均选用单一指标预测，并取平均值计算相应的ρ，每种工况下ρ最大的指标即该工况下的最优指标。然后针对不同工况下4种碾压次数均选用最优指标预测，并取平均值计算相应的ρ，最后计算不同工况下采用最优指标与采用单一指标的压实度预测准确率之间的差值，即采用最优指标比单一指标预测提升的准确率，范围为1%～22.5%，统计结果如表3所示。由表可知：对于不同工况下采用最优指标比采用单一指标的压实度预测准确率均有一定的提升；不同压实度质量评估指标在8种工况下的适用性有所不同，在不同工况下选取最优指标预测压实度，压实度预测准确率平均提高9.575%。

3  最优指标类型预测

采用支持向量机（support vector machine，SVM）、 逻辑回归（logistic regression）、 k最近邻（k-nearest neighbor，KNN）、 决策树（decision tree，DT）、 朴素贝叶斯（nave Bayes）法5种传统的机器学习方法分别进行训练学习。

对8种工况下的320个样本进行训练学习。每个样本对应一组标签，包括振动轮振幅A、 压路机的激振频率Ω、 沥青路面摄氏温度θ、 沥青刚度k2、 沥青阻尼c2、 振动轮振动加速度z··、 振动轮碾压次数N。每个样本同时对应一组特征值为响应的vcm、 vcc、 ks、 ω这4个指标中最优指标的类型，将特征值与标签一一对应组合在一起，得到样本集。然后将样本集按照测试集与训练集中样本个数之比为3∶7的比例随机分配。最终对4个指标进行分类学习，以实现根据已有样本在不同工况下寻求最优指标，并以成功寻求最优指标的概率作为机器学习算法的压实度预测准确率。

5种传统机器学习方法预测最优指标类型准确率的统计结果如表4所示。 由表可知， 决策树和朴素贝叶斯法的压实度预测准确率较高， 其中朴素贝叶斯法的压实度预测准确率最高， 可达96.22%， 因此在实际工程中可以使用朴素贝叶斯法寻求最优指标。

4  路基压实现场试验

4.1  试验条件与仪器

4.1.1  试验条件

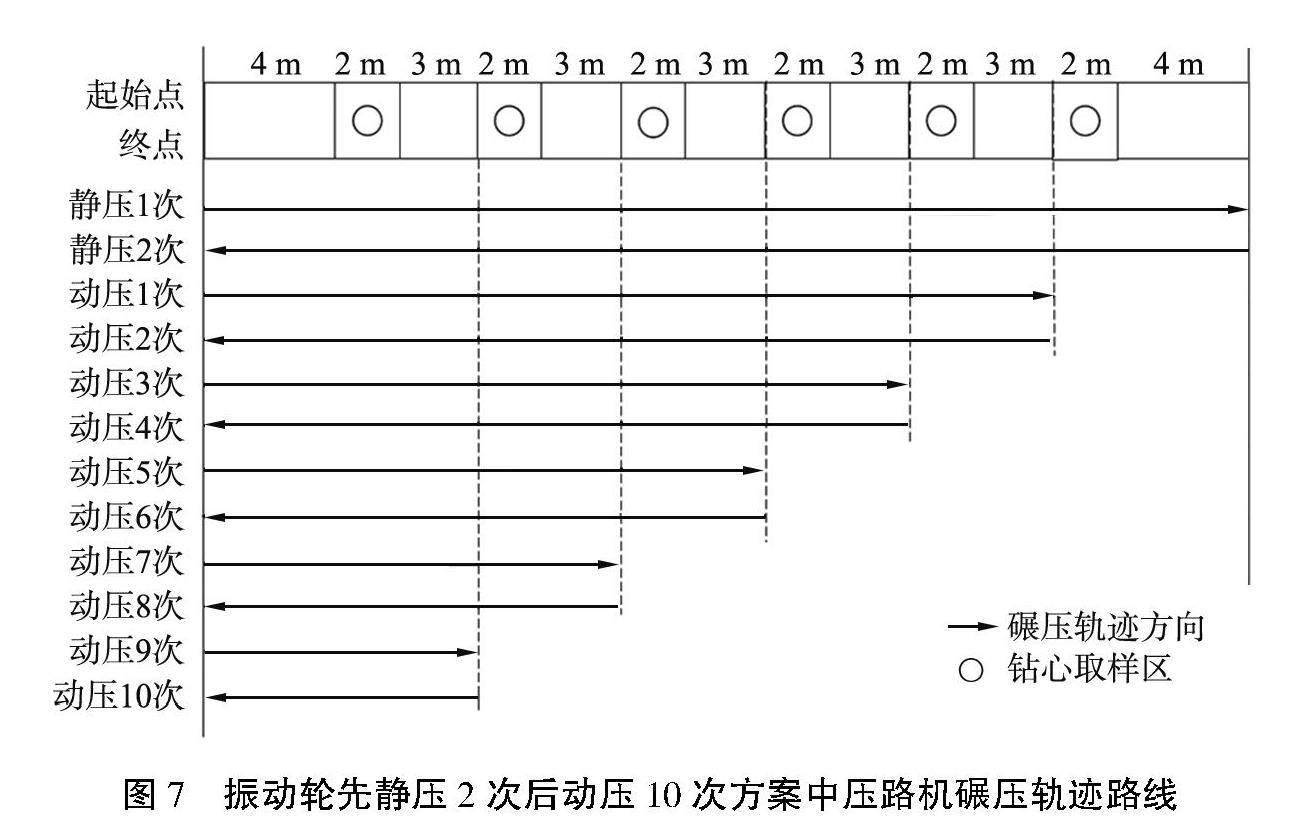
为了对本文模型进行验证， 开展路基压实现场试验， 施工前、 后现场试验实景如图6所示。 试验路段面层采用AC-25型改性沥青混凝土铺筑， 厚度为4 cm。 考虑到与正常施工工序相吻合， 采取振

动轮先静压2次后动压10次的方案， 碾压轨迹路线图如图7所示， 其中箭头方向为碾压轨迹方向， 采样长度、 宽度分别为35、 2.2 m， 分为13个区域。 考虑到两端位置处的机械启停会产生一定的误差， 启停区长度取为4 m。 图中圆圈的位置代表钻芯取样区， 取样区长度为2 m。 每个区域采样3个点并计算压实度的平均值。 2个圆圈之间的区域是压路机需要换向的位置， 因此将该区域预留出来， 并且考虑到压路机的车长，换向区长度取为3m。虚线

位置是压路机每次要换向时前轮轴所在位置。 压路机按照碾压路线行驶， 最终从起始位置驶出实验区域。

4.1.2  试验仪器

试验数据采集仪器包括： 1）加速度传感器。 试验时， 加速度传感器垂直放置于振动轴中间位置， 如图8所示。 在采集数据前， 为了防止加速度传感器滑动， 先擦拭振动轴上的灰尘， 再用胶水将加速度传感器固定于振动轴。 2）动态信号采集仪。 作为中间媒介， 动态信号采集仪一端与加速度传感器相连， 另一端通过网线与计算机终端连接， 并把计算机终端放置在驾驶室内以便于对压实度进行实时监控。 3）手持式测温枪。

振动轴中间位置的加速度传感器

4.2  数据获取与处理

4.2.1  数据获取

连续采样10次动压时加速度时域、频域信号如图9所示。由图9（a）可知： 10次振动信号所含噪声比例较小；由图9（b）可知：振动轮的振动频率为50 Hz，与振动轮的理论振动频率近似相等，间接验证了信号采集的可靠性。利用测温枪测得的数据包括：出料温度为155 ℃；静压之前温度为120 ℃；动压过程全段路面不同测点温度为100～110 ℃； 动压

过程内部温度为120～130 ℃。压路机自始至终采用最高挡位振动，根据8种工况设置，将本次试验工况类型设置为工况5。

4.2.2  数据处理

根据图9（a）计算10次动压时加速度的幅值平均值，將5个区域钻芯取样所得的压实度与计算所得的加速度的幅值平均值一一对应。由于第6次动压区域中有井盖导致数据错误，因此对该数据进行合理估值，并对第1、 3、 5、 7、 9次动压时的压实度数据进行插值，最终得到10次动压时加速度与压实度的统计结果，如表5所示。由表可知，在10次动压过程中，随着沥青路面压实度的增大，振动轮的加速度逐渐增大，与振动压实理论相吻合，间接验证了此路基压实现场试验结果的可靠性。

通过随机插值，对加速度和压实度进行样本扩充，扩充到320个样本。将压路机的机械参数输入到本文模型，其中除k2、 c2外都可以通过查找压路机相应型号的说明书得到。k2、 c2标定方法如下：先将压路机放置在压实度为100%的沥青路面上振动并测量加速度，然后分别将预估的k2、 c2输入到Simulink软件，通过不断迭代得到加速度对应的k2、 c2。将c2作为定值，根据沥青路面压实度为100%时的k2值确定k2的变化范围，从而完成对k2、 c2的标定。

统计利用朴素贝叶斯算法训练学习后，碾压次数为10时采用最优指标与单一指标的压实度指标相关系数ρ，结果如表6所示。标注*的数值对应的该碾压次数时ρ最大，即该碾压次数时的压实度质量评估指标为最优指标，并以该最优指标作为每次采用最优指标的压实度预测准确率。由表可知：当采用单一指标时，利用ω预测的压实度预测准确率最佳，为74.31%；当采用最优指标进行预测时，压实度预测准确率为80.11%，比采用单一指标时的压实度预测准确率提高了5.8%；在同一种工况下，不同碾压次数时不同指标的适用性存在差异，对于不同工况选取最优指标可以使压实度预测准确率提高5.8%。

5  结论

本文中通过对实际工程中沥青路面上不同压路机的振动规律进行对比，构建振动压路机-沥青路面系统动力学模型，结合机器学习和Simulink模拟仿真，对沥青路面压实度进行质量评估，并利用路基压实现场试验数据对采用最优指标代替单一指标后压实度预测准确率的可靠性进行验证，得到以下主要结论：

1）不同压实度质量评估指标在8种工况下的适用性存在差异，对于不同工况选取最优指标可以使压实度预测准确率提高9.575%。

2）相对于支持向量机、 逻辑回归、 k最近邻、 决策树，朴素贝叶斯法更适合预测不同工况下最优指标类型，在预测最优压实度质量评估指标类型时准确率最高，为96.22%。

3）路基压实现场试验结果表明，即使在同一种工况下，相对于采用单一指标，不同碾压次数时采用最优指标预测能使压实度预测准确率提高5.8%。

参考文献：

［1］  WANG L B， 王含笑， 赵千， 等. 智能路面发展与展望［J］. 中国公路学报， 2019， 32（4）： 50.

［2］  马建， 孙守增， 芮海田， 等. 中国筑路机械学术研究综述·2018［J］. 中国公路学报， 2018， 31（6）： 1.

［3］  黄志福， 梁乃兴， 赵毅， 等. 路面压实度自动连续检测技术［J］. 长安大学学报（自然科学版）， 2015， 35（6）： 24.

［4］  徐光辉， CHANG G. 智能压实测量值的发展方向［J］. 筑路机械与施工机械化， 2018， 35（4）： 19.

［5］  叶阳升，蔡德钩，朱宏伟，等.基于振动能量的新型高速铁路路基压实连续检测控制指标研究［J］.铁道学报，2020， 42（7）： 127.

［6］  贾通. 沥青路面智能压实系统关键技术研究［D］. 南京： 东南大学， 2020： 8.

［7］  RINEHART R V， MOONEY M A. Instrumentation of a roller compactor to monitor vibration behavior during earthwork compaction［J］. Automation in Construction， 2008， 17（2）： 149.

［8］  ANDEREGGR，KAUFMANNK.Intelligentcompactionwith vibratory rollers： feedback control systems in automatic compaction and compaction control［J］. Transportation Research Record： Journal of the Transportation Research Board， 2004， 1868（1）： 131.

［9］  KRBER W， FLOSS E H R， WALLRATH W. Dynamic soil stiffness as quality criterion for soil compaction［M］//Geotechnics for Roads， Rail Tracks， and Earth Structures. Lisse： Balkema， 2001： 196

［10］  LIU D H， LIN M， LI S. Real-time quality monitoring and control of highway compaction［J］. Automation in Construction， 2016， 62： 118.

［11］  吴龙梁. 基于能量耗散的路基连续压实控制技术研究［D］. 北京： 中国铁道科学研究院， 2020： 20.

［12］  PAULMICHL I， ADAM C， ADAM D. Parametric study of the compaction effect and the response of an oscillation roller［J］. Proceedings of the Institution of Civil Engineers： Geotechnical Engineering， 2020， 173（4）： 285.

［13］  代然， 胡水英， 張前， 等. 基于MATLAB/Simulink的垂直振动压路机动态性能的仿真研究［J］. 建设机械技术与管理， 2015， 28（6）： 93.

［14］  赵毅， 杨臻， 梁乃兴， 等. 沥青混合料压实度-振动加速度-温度关系模型［J］. 建筑材料学报， 2021， 24（3）： 621.

［15］  张世英. 关于振动压路机设计中土的参数的确定方法［J］. 工程机械， 1998（1）： 5.

［16］  陈博. 路基土压实度实时检测系统研究［D］. 西安： 长安大学， 2019： 34.

（责任编辑：王  耘）