基于有限元法的叉车式AGV门架系统结构分析

杜星杰 王飞

摘 要：叉车式AGV作为智能物流工具之一，是未来仓储物流、智能工厂的重要组成部分。本文以叉车式AGV为研究对象，通过有限元法建立其关键结构的分析模型，对其整体结构及关键零部件进行静力学和动力学分析与计算。结果表明，在极限受载状态下，门架系统各部分的结构强度、变形量及模态分析结果均符合设计要求，为验证叉车式AGV结构设计的合理性及后续结构优化提供了数据支撑和参考。

关键词：叉车门架；结构分析；有限元法；静力学；动力学

Abstract：The forklifttype Automated Guided Vehicle（AGV）is regarded as one of the intelligent logistics tools and a crucial component in the future of warehouse logistics and smart factories.This study focuses on the forklifttype AGV，utilizing the finite element method to establish an analytical model for its key structures.Both static and dynamic analyses and calculations were performed on the overall structure and critical components.The results indicate that，under extreme loading conditions，the structural strength，deformation，and modal analysis of various components of the gantry system meet the design requirements.This provides data support and reference for verifying the rationality of the forklifttype AGV's structural design and subsequent structural optimization.

Keywords：Forklift gantry；structural analysis；Finite element method；statics；dynamics

叉車是一种专门用于搬运、装卸货物、堆垛和短途运输的物料搬运工具［1］，以其易操作、低噪声、轻巧灵活等优势，广泛应用于工厂、仓库、车站、港口、机场、流通中心等各类场所［23］。近年来，随着叉车式AGV技术的快速发展和物流行业的高度自动化需求，叉车式AGV（下简称“无人叉车”）逐渐成为仓储物流装备中不可或缺的一部分。在无人叉车的设计和制造中，叉车门架作为其重要的组成部分之一，主要承担着叉臂的支撑和操控的重要角色。

叉车门架是叉车中的关键部件，通常包括支撑和固定货叉的框架系统。门架的结构设计将直接影响叉车的稳定性和承载能力。在一般情况下，门架系统由液压缸、叉架、门架、滚轮以及货叉等组件构成［4］，这些组件共同协作，使得叉车能够有效地搬运、装卸货物，同时保持平衡和稳定性。由于叉车常常不停歇地工作，叉车门架升降与前后倾动作极为频繁，其结构设计的合理与否关系到叉车部件运行过程中的应力分布、位移变化等状况，直接影响叉车门架的工作性能、工作效率和作业的稳定性，进而决定叉车的整体寿命。此外，叉车门架作为主要的承载结构，对多项技术参数都将产生影响，包括额定起重量、载荷中心距、最大起升高度和门架倾角等。因此，深入分析和研究门架的结构特性是提升叉车综合性能的关键［5］。童水光等［6］通过虚拟样机技术进行叉车的动力学仿真，模拟整个工作过程并生成门架在最危险工况下的载荷文件，然后利用有限元分析技术对叉车门架在这一最危险工况下进行静力学分析，以观察门架的应力和应变分布情况，最后针对货叉根部的应力集中问题，采用多目标数值优化法对货叉的设计参数进行调整，这一优化过程有助于提高叉车门架的结构稳定性和性能。方文勇等［7］通过FEM有限元分析，比较在不同条件下门架的应力变化情况，以判断是否需要增强特定部件的强度或者是否需要采取其他操作条件来确保门架的安全使用和寿命。王祖皓等［8］采用各级门架单独建模和整体建模的方法分别对其进行应力应变分析，然后对门架进行应力应变电测试验，结合结果进行评估，证明了在有限元分析时，采用整体建模的方法更高效、更可靠。李建萍等［9］通过静力学分析确定了叉车门架系统在正常工况下的受力状况，再通过对中横梁采用不同厚度、折弯半径和宽度等情况进行有限元分析，最后通过结果分析确定了适宜的中横梁尺寸，强调应尽可能增大中横梁的折弯半径以提高中横梁的强度。王天等［10］通过Pro/Engineer和ANSYS软件对叉车门架的有限元强度和刚度进行了分析，并进一步将有限元分析的计算结果与应力测试的试验值进行了合理性验证。周京京等［11］采用Solidworks建立了门架系统的实体模型，并通过COSMOSWorks进行了有限元分析，证明在危险条件下，门架的机械特性可以确保叉车的安全操作。Zhuang等［12］针对FEM有限元法分析的准确性不可靠，采用基于MPC184单元模拟方法的有限元法以及独立分析组件的方法对门架系统进行整体分析。

本文以叉车式AGV为研究对象，采用有限元法对其关键部件门架系统进行静力学和动力学分析与计算，旨在为该类叉车的强度、刚度和振动分析提供仿真数据，同时也为其结构优化提供了数据支撑和参考。

1 门架系统工作原理

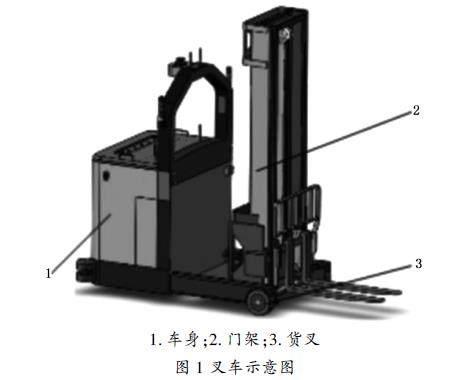
叉车的门架系统主要由货叉、货叉架、门架以及起升链条组成，如图1所示。货叉作为叉车升降货物的主要部件被安装在货叉架上，一般由一对L型的钢板组成，随货叉架上下移动进行装卸货物［13］。货叉架主要用于固定货叉等其他配件，在液压油缸和起升链条的共同作用下，货叉架沿门架内的轨道运动。门架是通过横梁连接而成的门式框架其内侧设有竖直轨道，可供货叉架滑移。起升链条为两条左右对称分布的片式链条，其一端绕过链轮与货叉架底端相连，另一端与门架的上横梁相连［14］。

门架系统运动状态可分为两个阶段：在货叉提升阶段，液压泵将液压油送入液压缸，当液压缸接收到液压油后，活塞开始向外伸出，驱动链轮带动链条，牵动货叉和货叉架起升。在货叉下降阶段，液压缸内的液压油通过阀门回流至油箱，液压缸的活塞则会缓慢返回，从而实现货叉的下降［1516］。

2 门架结构有限元分析

通过对叉车门架结构进行有限元分析能模拟和评估门架在各种负载和工作条件下的行为，包括强度、刚度、振动特性以及疲劳寿命，可帮助深入了解叉车的结构性能，用于预测结构在不同工况下的响应，确保门架在长期使用中的安全性和可靠性。

2.1 模型建立

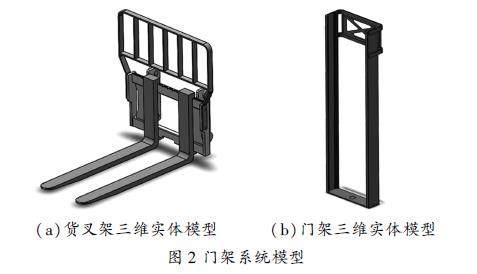
门架系统包含零件众多，为了提高计算效率，在保证计算精度的前提下对模型进行一些简化。本文以某型号平衡重式无人叉车为例进行分析，采用三维建模软件建立了门架的简化几何模型，只保留门架主体结构主要部分，简化了一些小型连接件等不重要的次要细节。如图2所示，简化后的模型由货叉架和门架组成。

2.2 材料属性

货叉架和门架结构材料选用65Mn，详细特性参数如表1所示。

2.3 门架结构静力学分析

静力学分析采用节点—位移模型，将几何模型离散化，单元位移和节点位移间的关系表达式如下：

{u}=［N］{δ}e（1）

其中：{u}为单元内部任意一点的位移列阵，［N］为形函数矩阵，{δ}e为节点位移矩阵。由式（1）可导出单元应变与节点位移的关系：

{ε}=［B］{δ}e（2）

其中{ε}为单元内部任意一点的应变列阵，［B］为单元应变矩阵。

根据本构方程，单元应力和节点的位移关系为：

{σ}=［D］{ε}=［D］［B］{δ}e（3）

其中{σ}为单元内任意一点的应力列阵，［D］为单元弹性矩阵，与材料相关。

根据变分原理，建立单元节点力和节点位移的平衡方程，并导出单元的刚度矩阵：

{f}e=［K］e{δ}e（4）

［K］e=∫BT［D］［B］dv（5）

其中{f}e为单元载荷列阵，［K］e为单元刚度矩阵。

将各单元刚度矩阵组合可得总体结构平衡方程：

{f}=［K］{δ}（6）

其中，{f}为总体载荷列阵，［k］为总体刚度矩阵。

将边界条件和载荷代入式（6）可求得各节点处的位移，再根据式（2）和式（3）可求得各单元处的应变和应力。

对整个门架系统进行静力分析以研究叉车在极端工作条件下的数据。当货叉架提升至最大高度时，对门架的底部和背部施加固定约束，对两个货叉架分别施加9800N的压力，以模拟货叉均匀受载2吨的情况。

P=FA=9800113653.87=0.086MPa（7）

在网格划分时进行网格灵敏度分析，当网格尺寸为5mm时，网格数量约为220万，此时网格质量为0.88；当网格尺寸为10mm时，网格数量为22.6万，此时网格质量为0873。因此为了节约计算成本，将网格尺寸设定为10mm，划分的网格模型如图3所示。分析计算得到门架系统满载下等效应力图及结构变形图（如图4、图5所示）。

由图4所示，在货叉表面均布载荷的作用下，货叉的应力主要集中在货叉折弯处，表现为拉应力，应力由折弯处向两侧递减。门架系统的最大应力发生在货叉根部，大小为102.12MPa，小于65Mn的屈服极限（785MPa），变化量均在弹性范围内的变形，不会出现塑性变形。在载荷作用下，货叉根部出現应力集中现象，有可能发生疲劳断裂。根据计算货叉安全系数为7.69，大于设计安全系数3.0。因此，货叉符合设计要求。由图5所示，在额定载荷作用下，货叉变形量由叉尖向根部减小。最大变形值位于货叉尖端，为13.23mm，校核其刚度：

13.23mm＜l50=96050=19.2mm（8）

式中l为货叉长度。从分析可知，货叉刚度在许用范围内，但是变形量较大，可以进行优化设计。

2.4 门架结构动力学分析

叉车式AGV在实际工作不仅会受到货物静载荷，还会受到随时间变化的动载荷。门架系统和叉车前桥连接，为了防止叉车工作中发生共振，对车身和门架系统进行振动分析是十分必要的。

常用模态分析微分方程为：

Mx¨+Cx·+Kx=ft（9）

式中：［M］为质量矩阵，［C］为阻尼矩阵，［K］为刚度矩阵，x¨为加速度矩阵，x·为速度矩阵，x为位移矩阵，f（t）为外激励矩阵，这里为零矩阵。根据叉车结构及各部件之间连接关系，设定阻尼刚度矩阵为零。多自由度无阻尼振动系统微分方程可表示为：

Mx¨+Kx=0（10）

综合考虑门架系统振动和路面激励带来的影响，选取前六阶作为频率提取范围。对门架进行前六阶模态分析，获得门架前六阶自由模态频率和振型，分别如表2门架前六阶振动频率和图6门架前六阶振型图所示。

如图6所示，门架不仅呈现纯弯曲振动，还表现出绕其中心旋转的振动。在前六个振型中，纯弯曲振型占据主导地位，对门架的影响最为显著。这些振动形式都会对门架立柱结构的刚度和强度产生影响。因此，在实际工程设计中，可以通过合理布置门架的质量、增加横梁数量、调整横梁布置位置等方法，有效降低振动对门架的不良影响。

一般情况下，路面激励的频率属于较低的范围，即时间频率在0.5～20Hz之间。通过对门架的前六个固有频率进行分析，发现门架的第一阶固有频率为29.846Hz，超出了常规的激励频率范围。这符合设计要求，意味着叉车在工作过程中门架不太可能发生共振现象。

门架由于底部固定在叉车前桥上，且重心位置极少发生变化，所以，刚度较大，产生的振动较轻。门架与车的振动频率不相等，因此不会产生共振现象，满足设计要求。

结语

本文以叉车式AGV为研究对象，运用静力学和动力学分析对叉车门架系统进行了研究，并采用有限元法对门架结构进行了仿真分析，结果表明，在静力学分析中，门架和货叉的强度刚度均符合设计要求，但货叉的变形量较大，需要进一步优化；在动力学分析中，门架与车身将不会发生共振，确保了无人叉车的运行平稳性。上述仿真结果为验证叉车门架的强度、刚度和振动频率提供了依据，同时也为门架系统的结构优化提供了数据支撑和参考。

参考文献：

［1］张义壮，冯川.电动叉车举升机构设计及有限元分析［J］.机械研究与应用，2020，33（03）：4851.

［2］赵子文，张其丰，吕岩军.叉车门架刚度有限元分析［J］.现代制造技术与装备，2022，58（02）：15.

［3］齐善朋，岳君.基于ANSYS的叉车外门架结构有限元分析［J］.科技创新与应用，2014（29）：61.

［4］陈利杰.叉车门架结构的改进与优化［J］.科技与企业，2016（04）：164.

［5］相曙锋.叉车门架强度分析与结构改进［J］.工程机械，2022，53（04）：2326+8.

［6］童水光，何顺，童哲铭，等.叉车门架动静态联合仿真及多目标优化［J］.机械设计，2018，35（12）：711.

［7］方文勇.FEM在叉车门架重叠度更改中的应用［J］.机械工程与自动化，2017（05）：8990.

［8］王祖皓，尹辉俊，张芸华，等.某叉车门架有限元模型评估［J］.广西科技大学学报，2015，26（04）：2125.

［9］李建萍，李泽阳，许金栋，等.叉车外门架中横梁的受力及有限元分析［J］.工程机械，2013，44（11）：4650+3.

［10］王天，韩振.3t平衡重式叉车门架有限元分析［J］.工程机械，2012，43（12）：2427+7.

［11］周京京，穆希辉，马振书，等.全向侧面叉车门架有限元分析及运动仿真［J］.起重运输机械，2009（02）：6568.

［12］Zhuang Y，Shan D Z，Zhang Q.Finite Element Analysis of a Forklift Truck Mast System［J］.Applied Mechanics and Materials，2014，2963（494495）：668672.

［13］姚鍇，袁晓金，段志梅，等.叉车门架装置类型的探讨［J］.机电工程技术，2022，51（02）：189191.

［14］丁亮.叉车起升系统设计思路的探讨［J］.物流技术与应用，2021，26（05）：151153.

作者简介：杜星杰（1988— ），男，汉族，内蒙古乌兰察布市凉城县人，本科，技师，研究方向：车辆工程。