面向工程应用的大数据技术实践教学探索

田入运， 曹一涵

（南京信息工程大学自动化学院，南京 210044）

0 引 言

随着信息技术的飞速发展和互联网智能化的不断深入，大数据技术在工程应用中扮演着日益重要的角色［1］。大数据以其高速度、大容量、多样性和价值密度高的特点，正在引领着全球各行各业的变革和创新［2］。作为大数据技术的核心，数据科学已经成为培养学生的关键要素之一。然而，数据科学与大数据技术实践教学仍面临一些挑战和问题，传统的大数据实验教学模式往往以理论知识或简单实践为主，忽视了对工程应用能力的培养。仅仅靠理论学习已经不足以满足工程应用的需求［3］。因此，需要重新思考面向工程应用的数据科学与大数据技术实践教学的方式和方法，培养学生具备解决实际问题能力和思维。

如何确保教学内容与工程实践紧密结合，培养学生具备数据科学和大数据技术的综合能力，是当前亟待解决的问题［4-6］。本文聚焦于将理论知识与工程应用紧密结合，培养学生在工程场景下的数据科学应用能力，提出一种结合问题导向学习（Problem-based Learning，PBL）、探究式学习（Inquiry-based Learning，IBL）和学习成果导向（Outcome-based Education，OBE）相结合的PIO（Problem-Inquiry-Outcome）综合学习方式［7］。

PIO综合学习方式可以将不同的学习方法和理念结合起来，以提供更全面和综合的教育体验。PBL、IBL和OBE方法可以相互融合，以达到更好的学习效果［8］。本文旨在利用PIO 综合学习方式，探索面向工程应用的数据科学与大数据技术实践教学的改革策略。探讨如何设计与实际工程应用问题相关的教学内容和案例，以引发学生的兴趣和培养他们的实践能力；研究如何利用创新的教学方法和工具，提高学生在大数据技术领域的学习效果和应用能力；关注评估和反馈机制，以确保教学过程的持续改进和学生能力的有效提升。

1 工程应用问题案例

以工程项目“基于边缘计算的微动勘探横波速度结构即时成像系统”为例，从中提炼出“基于负载预测的负载分配与计算资源优化”问题设计成学生的实践内容。为完成横波速度结构即时成像，首先选取合适的横波速度结构成像算法。空间自相关法从微动信号的垂直分量中提取瑞利波相速度频散曲线，通过对瑞利波频散曲线的反演估算介质横波速度结构，是目前快速有效确定沉积层横波速度结构的方法之一［9］。本项目采用的基于空间自相关法的微动探测横波速度结构成像的任务处理，其总体结构如图1 所示。

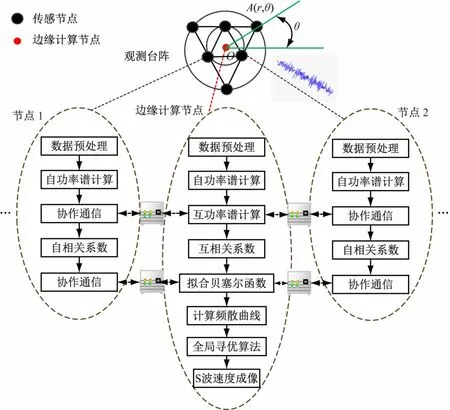
图1 基于空间自相关法的微动探测即时成像结构示意图

由于微动勘探所采用设备的计算能力和计算资源有限，需要采取措施来避免边缘计算节点负载过重，从而导致计算任务在边缘计算节点排队等待的严重延迟情况。边缘计算节点承载的负载远高于感知节点，在面对负载变化时，固定数量的边缘计算资源可能会面临过供应和欠供应的问题，进而影响成像的即时性和稳定性（PBL），为了降低任务排队延迟，需要合理分配计算资源，而计算资源的分配依赖于负载，因此，首先需要探究边缘网络的负载动态变化规律（IBL），根据负载的变化规律，实现对计算任务负载的预测，从而根据负载分配计算资源，完成横波速度结构的即时成像（OBE）。

在确定好项目架构后，按模块关联项目任务，以任务关联相关课程。如表1 所示，“基于负载预测的负载分配与计算资源优化”项目包含的3 项任务分别关联到数学建模、大数据采集与预处理、机器学习、Python程序设计、深度学习和最优化理论与方法课程［10］，这些课程都是大数据类专业必修的专业课，对学生进一步加深对于专业的认识和理解，巩固专业基础有较好的促进作用。同时，通过任务之间的关联，学生能够在项目中形成全局的视角和思维，使得项目的目标和任务更加协调和高效。

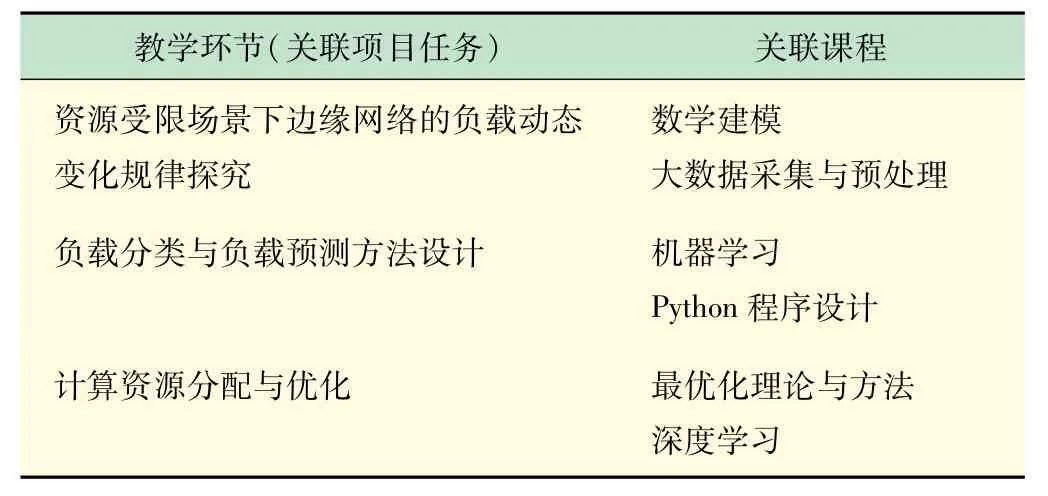
表1 工程项目驱动的大数据类专业课教学设计

2 实践教学过程设计与实施

2.1 教学过程设计

项目“基于负载预测的边缘计算负载分配与计算资源优化”包含3 个模块，引入6 门课程，在教学设计过程实施中按课程展开，通过项目驱动的课程教学设计，学生能够在具体项目的实践中学习和应用数学建模、机器学习、Python 程序设计、最优化理论与方法和深度学习等专业知识和技能，专业课教学过程设计如表2 所示。

表2 工程项目驱动的大数据类专业课教学过程设计

2.2 教学过程实施

（1）数据采集与预处理。边缘网络负载原始数据来源于微动勘探设备，利用勘探设备中边缘节点和传感节点处理一定计算任务的响应时间作为负载指标。如果条件不允许，也可利用多台电脑处理一定的计算任务进行测试和收集数据，本文收集的数据集有2 个维度（本地响应时间和外地响应时间），各有70 000 多条实测数据，部分数据集展示如图2 所示。

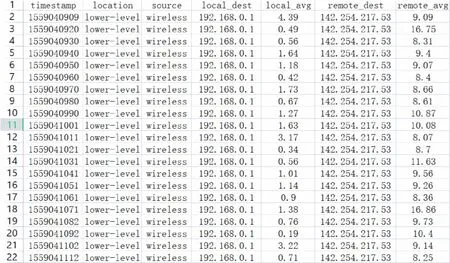
图2 部分原始数据集

获取原始数据后，需要对原始数据进行预处理，选取本地响应时间作为指标，对于大量无序的数据集，包括清洗、转换和准备数据，以便后续的分析和建模。负载数据预处理的步骤如图3 所示。

图3 负载数据预处理

（2）负载动态变化规律探究。由于边缘计算节点汇聚和处理各个感知节点卸载而来的任务，若系统中边缘计算节点的任务队列向量Q（t）保持稳定，即

式中，

同时，负载队列向量也需保持稳定，即

式中，

则系统保持稳定［11］。为了避免边缘计算节点负载过重而导致任务在边缘计算节点的严重排队延迟情况，边缘计算节点的任务队列和负载队列应该首先保持稳定。边缘计算节点承载的负载远高于感知节点，在面对负载的变化时，固定数量的边缘计算资源可能会面临过供应和欠供应的问题，进而影响成像的即时性和稳定性，如图4 所示。

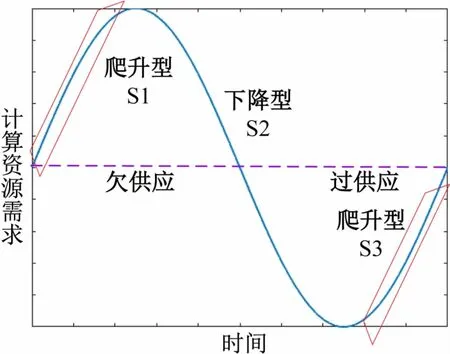
图4 计算资源的过供应和欠供应

观察成像服务的网络负载变化趋势发现，其负载呈现出周期性变化，虽然某些时刻仍具有一定的随机性和突变性，但可直观地按照其变化趋势与特点将该负载划分为爬升和下降两种类型，根据此特点，需进一步进行负载分类。

（3）负载分类及负载预测方法设计。根据图4 的负载变化趋势，拟采用无监督机器学习K-means 算法作为训练数据集分类和标注处理的首选方法。该算法以欧几里得距离为衡量目标，根据设定的类别数量，经过一定次数的迭代后，距离相近的数据会被划分到相同类别中。然而，研究中发现仅使用原始的网络负载数据和K-means算法难以按照设定类别对训练数据集进行有效划分。假设在负载训练数据集中有3 组数据S1、S2 和S3，其中S2 为下降类型，S1 和S3 为爬升类型，如图4 所示。S1 和S2 的最大欧几里得距离小于S1 和S3 的最大欧几里得距离。因此，K-means 算法存在很大的概率将S1 和S2 划分为相同的类型，而S1和S3 划分为不同的类型。观察到这两种类型的网络负载数据变化趋势，可发现一阶梯度特征能有效地表征爬升和下降类型网络负载数据的变化特点。因此，本文采用一阶梯度特征和K-means 算法相结合的方式训练一个分类神经网络模型进行分类。

计算资源按需分配与弹性调度优化的关键是提高边缘计算节点网络负载的预测精度。本文采用基于自适应LSTM神经网络模型设计一种负载预测方法，该方法根据输入网络负载数据的变化趋势对负载分类，并根据分类结果自适应地将输入的负载数据调度到与之类型相匹配的LSTM负载预测模型中进行预测。自适应LSTM 神经网络模型训练和预测方法如图5所示。

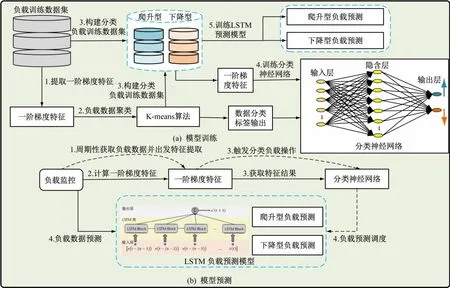
图5 自适应LSTM神经网络模型的（a）负载训练和（b）负载预测

在训练自适应LSTM 负载模型过程中，选择了1 000 轮的迭代次数，以保证模型可以充分学习时序序列中的规律。每进行100 轮迭代，都会记录训练误差和验证误差，并进行监测，如果发现模型的训练误差和验证误差达到了平稳状态，就可以终止训练。为了减小误差，实验采用了反向传播算法来更新模型的参数，使用随机梯度下降法进行参数更新，以提高训练效率。同时，也采用了dropout 技术来减少过拟合的影响。最终，在进行1 000 轮迭代后，得到了一个自适应LSTM负载预测模型。训练过程中，不断调参重新训练，对于梯度下降算法的选取，最终确定了adam 自适应梯度下降法。经多次训练，确定初始学习率为0.005 与学习率下降因子0.1，得到了较好的训练效果，训练集与测试集预测结果如图6 所示。

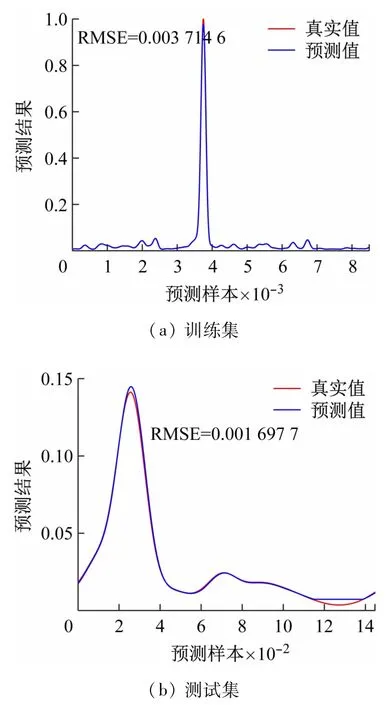
图6 训练集和测试集预测结果

对于负载预测，可以通过向本研究所提出的LSTM模型输入一定长度的历史数据，来预测接下来一段时间内的未来数值。同时，也可以通过递归方式，对模型的预测结果进行迭代，从而得到多个时间段的预测结果。图7 展示了本模型的预测结果，在原始数据的基础上对未来的500 个数据值进行了预测。

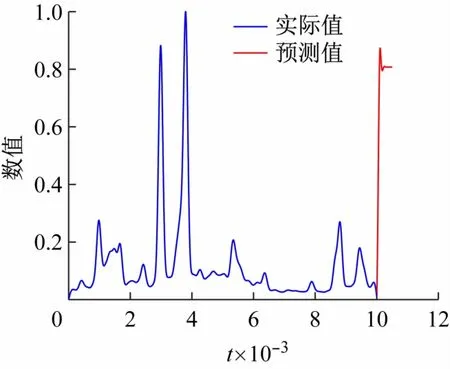
图7 负载预测结果

（4）计算资源优化。计算资源的优化依赖于计算任务的分配［12］，根据图1，假定计算任务卸载模型为二进制卸载，即可以在普通传感节点上进行处理，也可以卸载到边缘计算节点处理，可表示为：

式中，

分别表示待处理计算任务在时隙t时分别在本地执行和边缘计算节点执行的情况。假定时隙t的集合为T=｛0，1，2，…｝，并且每一个时隙的长度为τ，用随机变量A（t）表示时隙t内到达传感节点的计算任务，由任务处理系统的性质假定A（t）满足独立同分布，并且E［A（t）］=λ ＜∞，其中λ 已知。设时隙t内CPU 周期频率为f（t），那么时隙t中的传感节点在本地执行的计算任务量可以表示为

式中，L为传感节点上处理1 bit的数据需要的CPU周期数量，那么传感节点在时隙t执行计算任务的时间可以表示为：

假设边缘计算节点上有足够的资源进行计算任务。当选择卸载待处理任务至边缘计算节点进行处理时，需要考虑待处理任务上传到边缘计算节点的传输时延以及将处理好的数据反馈的传输延迟，由于反馈的传输延迟远小于上传的传输延迟，所以忽略其执行延迟及反馈的传输延迟［13］。假设传感节点通过正交频分多址（OFDMA）的方法接入边缘计算节点，信道带宽是固定的，即采用无干扰的信道模型［14］，则传输速率计算公式如下：

式中：P（t）为普通传感节点的传输功率；W为系统的带宽；N0为噪声的功率谱密度；H（t）为普通传感节点到边缘计算节点的信道功率增益，

g0为路径损失常数；ε 为相关比例参数；d0为参考距离；θ为路径损失函数；d为普通传感节点到边缘计算节点的距离。在时隙t内传感节点卸载到边缘计算节点上的任务量可以表示为

普通传感节点在时隙t卸载计算任务到边缘计算节点的传输时间可以表示为

采用在预定义的优化成像时延的方式。定义传感节点在时隙t时的能耗

式中：Elocal（t）为传感节点在t时隙内本地执行的能耗；Etrans（t）=P（t）·τ在时隙t内计算任务卸载到边缘计算节点的传输能耗。传感节点在时隙t时离开队列的数据量

协同计算任务的时延主要包括计算时延和传输时延。可以用T（t）表示时隙t内任务的时延，具体表示为

式中，To（t）表示数据量在边缘计算节点的等待时延和计算时延。因为边缘计算节点有充足的计算资源，设其计算周期频率为定值fmax。引入Et表示时隙t内的平均能耗，在每时刻满足独立同分布且引入Eavg平均能耗的最大值，则普通传感节点在时隙t的能耗均值满足：

基于以上约束，任务时延的最小化问题可以建模为如下最小化问题：

式中：约束式（14a）为输出能量约束，在每个时隙输出能耗不能超过Emax；约束式（14b）和（14c）分别为允许发射功率和CPU周期频率约束；约束式（14d）为计算任务卸载决策的0—1 整数规划约束。

时延最小化问题属于随机优化问题，即需要确定每个时隙中传感节点的最优计算资源分配才能最小化时间延迟。李雅普诺夫优化理论是处理随机优化问题的有效方法［15］。由于计算任务的到达时刻及任务队列的长度是随机且不可预测的，所以卸载决策的选择只能取决于当前队列积压情况以及节点计算资源分配等信息。而该优化理论仅使用当前网络中节点计算资源和当前队列长度，并且不需要计算卸载或节点计算资源状态的先验知识，能够在保证队列系统稳定性的前提下同时实现卸载优化与李雅普诺夫漂移优化，漂移优化过程就是求解最优资源分配过程，因此可以实现在线决策。

按照李雅普诺夫优化理论的需要，用两条排队队列分别表示传感节点与边缘计算节点的任务队列缓冲区，到达但还没有执行的任务将会进入一个队列缓冲区。Ql（t）为时隙t内传感节点的队列，Qo（t）为时隙t内边缘计算节点的队列。初始条件为0，即Q｛l，o｝（0）=0。Qo（t）队列的更新公式为：

式中，Ao（t）表示时隙t中到达边缘计算节点的数据量。针对上述问题，本项目通过对负载进行提前预测，根据负载预测结果对计算资源进行分配和调度，避免计算资源分配与调度滞后于负载变化问题。

在求解过程中获得的值表示最优计算卸载和计算资源分配。该算法利用深度神经网络（DNN）实现边缘计算资源分配。根据输入的参数和常量初始化仿真场景和算法参数。创建一个DNN 对象来存储和处理神经网络。采用的李雅普诺夫优化的计算资源分配算法如下：

?

根据上述算法，对计算资源分配算法进行测试，如图8（a）所示。计算模式选择的趋势大致可以分为两个阶段。第1 阶段涵盖时隙0 ～200，其中算法仍处于初始迭代阶段，队列尚未收敛，导致处理任务的计算模式选择出现较大波动。该阶段本地执行的任务比例高于边缘计算节点。第2 阶段涵盖时隙200 ～5 000。随着时隙数量的增加，边缘计算节点执行计算任务的比例逐渐增加，计算选择模式的曲线趋于平滑，表明在这一阶段倾向于将任务卸载到边缘计算节点执行，从而最大限度地减少系统模式下的能耗。图8（b）显示了在相对距离为200 m的普通传感节点和边缘计算节点的前1 000 个时隙期间所选计算模式选择的详细视图，可看出早期阶段计算模式选择的变化更为明显。在这个阶段，本地执行的计算比例高于边缘计算节点执行的计算，并且随着时间的推移保持稳定。当计算任务选择的概率为0.6 时，所需时隙的数量达到最大值120。

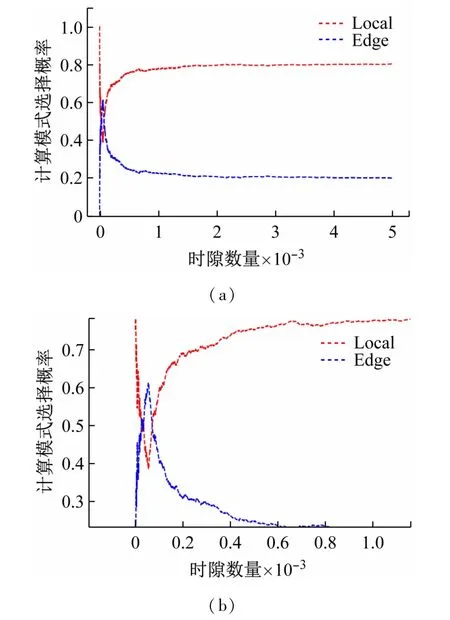
图8 （a）计算任务的节点选择和时隙数量和（b）前1 000个时隙期间所选计算模式

对传感器节点和边缘计算节点的任务队列积压是评价计算资源分配算法的重要指标。随着时隙数的增加，队列积压不断变化，队列积压波动越小，表示队列越稳定。图9（a）说明了当相对通信距离为200 m时，传感器节点、边缘计算节点的平均队列长度和整体队列积压的变化。平均队列长度最初随着时隙的推移而增加，然后逐渐达到一定值，并表现出周期性波动，表明队列达到了稳定状态。

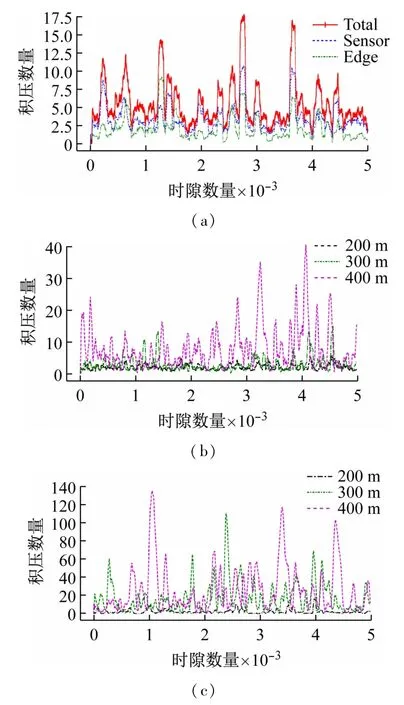
图9 （a）200 m通信距离处传感器节点、边缘计算节点的平均队列长度和总积压（b）不同距离处传感器节点的队列积压的比较（c）不同距离的边缘节点的队列囤积的比较

图9（b）和图9（c）展示了传感器节点在3 个不同距离（200、300 和400 m）的队列积压的比较。从图中可以明显看出，传感器节点和边缘计算节点的队列积压在200 m的距离上都表现出轻微的波动，虽然波动随着距离的增加而增加，但即使在400 m的距离上，队列积压也保持稳定，体现了处理器和内存性能的影响。

影响微动探测即时成像的最重要因素是执行延迟，平均队列长度是执行延迟的指标。由图可知，平均队列长度的最小收敛值出现在200 m 处，表明该计算资源算法在执行延迟方面具有更好的性能。随着距离的增加，节点执行计算任务的延迟也会增加。图10 提供了3 种不同距离上延迟大小的比较，每个距离处的延迟最初随着间隔的数量而增加，最终降低到稳定值。当相对距离为200 m时，时间延迟约为9 ms。在相对距离300 m处，时延最初增加到18 ms，略有增加，然后逐渐接近15 ms。同样，当相对距离为400 m 时，时间延迟首先上升到20 ms，然后慢慢接近17 ms。延迟大小表明，200 m的相对距离是最佳位置，延迟的稳定性验证了计算资源分配算法的可行性。

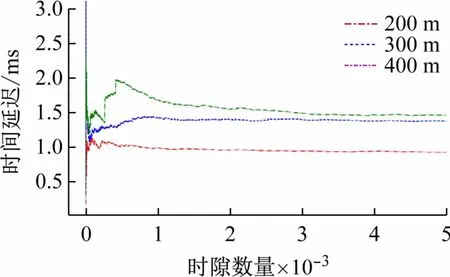
图10 不同距离执行延迟的比较

3 实验教学效果评价

表3 展示了面向工程应用的大数据专业实践教学考核内容、评价内容、考核能力和评价指标可用于对学生在实践教学中的表现进行评估和反馈，以促进他们的学习和能力发展。

表3 面向工程应用的数据科学与大数据技术实践教学考核

基于PIO理念，面向工程应用的实践教学可实现以下目标：

（1）在综合学习的环境中，学生可以通过问题导向学习方法来引发好奇心和主动学习的动力。随着问题的提出，学生可以利用探究式学习的方法，深入研究问题、收集信息、进行实证和分析。同时，学习成果导向的方法可以帮助学生明确学习目标和成果，将问题导向和探究过程与学习成果相结合，形成具体的学习成果和评估标准。

（2）综合学习方式强调学生的主动参与和自主学习，培养学生的解决问题的能力、批判性思维和创造力。学生通过参与问题解决和探究活动，不仅能够掌握必要的知识和技能，还能够培养解决实际工程问题和应对复杂情境的能力。

（3）教师在综合学习环境中的角色是指导者和支持者。教师一方面可以设计有挑战性和启发性的问题，提供工程应用问题的材料，支持学生的探究活动，根据学生的需要和学习进展提供个性化的支持和反馈，确保学习目标和评估标准的清晰和可衡量性。另一方面，教师也要关注个体差异和学生需要，进行充分的规划和组织，创造多样化的学习机会和环境。

（4）综合学习方式可以为学生提供更具意义和深度的学习体验，并培养他们在不同情境下的综合能力和学习技能。适应性强的综合学习方式更加贴近现实需求，并促进学生的长期发展和成就。

以工程项目驱动的大数据类课程教学改革自运行以来，目前已有2 届本科生开展竞赛驱动的课程教学，学生在阿里云天池大赛、CCF 大数据与计算智能大赛、全国人工智能大赛等省级以上学科竞赛获奖70 余项，参与教师横向科研工程项目30 多项，发表中文核心期刊论文6 篇，授权实用新型专利和软件著作权多项。学生在工程项目应用和学科竞赛中取得的成就也展示了其解决实际问题的能力，这些成果不仅是教学改革的成功范例，也为今后的课程教学提供了宝贵的经验和启示。

4 结 语

本文探讨了在面向工程应用的数据科学与大数据技术实践教学中，以工程项目为背景设计的实践课程内容。通过针对工程项目“基于边缘计算的微动勘探横波速度结构即时成像系统”的学生实践，设计了负载动态变化规律探究、负载预测模型设计和实施、计算资源分配方案设计和优化3 个项目内容。项目内容不仅考察了学生的数据科学与分析能力、模型建立与应用能力、问题解决与创新能力和团队合作与沟通能力。在教师的角色转变方面，本文提出了从知识灌输者转变为学习指导者的转变，这种转变将促进学生的实践能力和创新思维的培养，使其能够更好地适应工程应用的需求，并为社会和行业的发展做出贡献。