2-D离散时滞系统的新时滞相关稳定性准则

彭丹 张明霞

摘  要：研究了具有时变时滞的二维（two-dimensional，2-D）离散系统的时滞相关稳定性问题.所创建的Lyapunov-Krasovskii泛函（Lyapunov-Krasovskii functionals，LKFs）考虑在二次项和单项求和项中引入时滞相关矩阵，包含了更多的状态信息.同时在单项求和项中引入增广向量矩阵，并给出适用于2-D系统的多重辅助函数不等式和互凸组合不等式，用于处理LKFs差分，以便降低计算负担.然后，为具有时变时滞的2-D离散系统推导出保守性更小的穩定性准则.通过两个数值算例验证了所设计方法的有效性和优越性.

关键词：二维离散系统;时变时滞;Lyapunov-Krasovskii泛函;多重辅助函数不等式;互凸组合不等式

中图分类号：O231      文献标志码：A文章编号：1000-2367（2024）03-0050-12

二维（2-D）系统通常被视为有两个独立的自变量.由于其在自动控制、迭代学习控制、多维数字滤波器等多个学科和工程领域发挥着重要作用，2-D离散系统越来越受到关注［1-2］.因此，许多学者对2-D离散系统进行了广泛研究，并取得了许多成果［3］.

众所周知，在很多实际系统中，时滞都是不可避免的，例如通信系统，电力系统，网络传输系统［4-6］.所以时滞是现实生活以及实际工程系统中有待解决的问题［7-11］.时滞的存在，一方面使系统的动态性能变差，甚至造成系统的不稳定.另一方面，在一些控制系统中，人们可以利用时滞来提高控制效果，比如在重复控制系统中，需要利用时滞来达到预期目标［12-15］.为了更好地利用时滞解决实际问题，避免其不良后果，有必要从理论角度更加深入地分析和理解时滞对动态系统的影响.

由于离散系统更适用于实际生活而逐渐受到更多的关注，离散系统的稳定性也因此成为一个热门话题.因此，针对1-D离散系统中LKFs的设计方面已经得到突破［16-23］.文献［24］构建了一个新的LKFs，其中包含两个时滞相关矩阵，一个具有单项求和项，另一个具有二次项，用来研究离散时滞系统的稳定性.但是，由于2-D系统的结构，即信息传播发生在两个独立的方向上，选取的LKFs通常导致系统的保守性较大［25］.目前对于2-D离散系统的研究，文献［26］采用LKFs方法研究了2-D连续离散系统的有限区域耗散控制问题.文献［27］给出了2-D离散系统的稳定性准则，其中LKFs是使用LMIs的区间时变时滞结合时滞分区的方法所设计.文献［28］研究了基于时滞分区的LKFs来分析2-D离散系统的时滞相关稳定性问题.文献［29］构建的增广LKFs充分利用了时滞变化的信息.以上针对1-D离散系统研究的文献都在LKFs的构造中进行了创新，同时考虑到了更多的状态信息.然而，到目前为止，还没有关于在2-D离散系统中将时滞相关技术扩展到LKFs求和项的文章.基于上述分析，本文的主要创新点如下：

收稿日期：2023-01-12;修回日期：2023-03-17.

基金项目：国家自然科学基金杰出青年科学基金（61825304）；河北省自然科学基金（F2022203085）；河北省省级科技计划资助（F2020203037）；河北省自然科学基金创新研究群体项目（F2020203013）.

作者简介（通信作者）：彭丹（1978-），女，吉林吉林市人，燕山大学教授，博士，研究方向为2-D非线性系统和时滞系统，E-mail：dpeng1219@163.com.

引用本文：彭丹，张明霞.2-D离散时滞系统的新时滞相关稳定性准则［J］.河南师范大学学报（自然科学版），2024，52（3）：50-61.（Peng Dan，Zhang Mingxia.New delay-variation-dependent stability criterion for 2-D discrete systems with delays［J］.Journal of Henan Normal University（Natural Science Edition），2024，52（3）：50-61.DOI：10.16366/j.cnki.1000-2367.2023.01.12.0001.）

1）建立具有时变时滞的2-D离散系统模型，将时滞相关矩阵P1（d1（i）），P2（d2（j）），Q1（d1（i）），Q2（d2（j））和增广向量矩阵ξk（i，j）（k=1，2，3，4）分别添加到二次项和单项求和项中，同时所创建的LKFs还包含三重求和项，例如5=∑-d1m-1s=-d1M∑-d1m-1u=s∑-1ν=uyT（i+ν，j）R1y（i+ν，j）（与水平方向相关），这包含了有关时滞上界和下界的更多信息，从而得到保守性更小的稳定性准则和较大的时滞上界.

2）新的2-D加权求和不等式应用于LKFs前向差分中有限和项的处理，加权不等式的存在简化了计算过程，降低了系统稳定性准则的计算负担，同时促进了2-D系统理论的发展.然后根据LMIs推导出新的时滞相关稳定性准则.与参考文献中时滞相关的稳定性结果相比，本文推导的结果利用的决策变量的数目更少，并且适用于更广泛的时滞范围.

1  模型描述

考虑2-D离散时变时滞系统，如下：x（i+1，j+1）=A1x（i，j+1）+A2x（i+1，j）+A1dx（i-d1（i），j+1）+A2dx（i+1，j-d2（j）），（1）

其中x（i，j）∈Rn是状态向量，i，j∈N.A1，A2，A1d和A2d是具有适当维度的常量矩阵.d1（i）和d2（j）分别是水平和竖直方向上的时变时滞，分别满足： 0＜d1md1（i）d1M，0＜d2md2（j）d2M，μ1mΔd1（i）=d1（i+1）-d1（i）μ1M，μ2mΔd2（j）=d2（j+1）-d2（j）μ2M，（2）

其中d1m，d2m，d1M和d2M是常量正整数，表示时滞边界，μ1m，μ2m，μ1M和μ2M是常量整数，表示时滞变化范围.边界条件假定为：x（i，j）=φi，j，0ir1，j=-d2M，-d2M+1，…，0，

x（i，j）=0，i＞r1，j=-d2M，-d2M+1，…，0，x（i，j）=ψi，j，0jr2，i=-d1M，-d1M+1，…0，

x（i，j）=0，j＞r2，i=-d1M，-d1M+1，…，0，φ0，0=ψ0，0，（3）

其中r1和r2是正整数.

鉴于上述形式，本文旨在找到新的稳定性准则保证系统（1）稳定.为了推导出本文结果，提供了适用于2-D系统的多重辅助函数不等式［30］以及互凸组合不等式［31］.

引理1［30］  对于给定的正定n×n矩阵R，3个给定的非负整数a，b，k满足a＜bk，一个向量函数x（·）∈Rn并且表示y（s，j）=x（s+1，j）-x（s，j），y（i，s）=x（i+1，s）-x（i，s），有：1）∑-a-1s=-byT（s，1）Ry（s，1）1b-a（0a，b）TR（0a，b）+3b-a（1a，b）TR（1a，b）+5b-a（2a，b）TR（2a，b），

2）∑-a-1s=-b∑-a-1u=syT（u，1）Ry（u，1）2（3a，b）TR（3a，b）+4（4a，b）TR（4a，b），（4）

其中0a，b=x（-a，1）-x（-b，1），1a，b=x（-a，1）+x（-b，1）-2b-a+1∑-au=-bx（u，1），

2a，b=x（-a，1）-x（-b，1）+6b-a+1∑-au=-bx（u，1）-12（b-a+1）（b-a+2）∑-as=-b∑-au=sx（u，1），

3a，b=x（-a，1）-1b-a+1∑-au=-bx（u，1），

4a，b=x（-a，1）+2b-a+1∑-au=-bx（u，1）-6（b-a+1）（b-a+2）∑-as=-b∑-au=sx（u，1）.

引理2［31］  对于任何向量ξ∈Rmx，矩阵R1，R2∈Snx+，S∈Rnx×nx，W1，W2∈Rnx×mx和实标量α＞0，β＞0满足α+β=1，满足以下不等式：1αξTWT1R1W1ξ+1βξTWT2R2W2ξξTW1W2TR1SSTR2W1W2ξ，（5）

满足R1SSTR20.

2  稳定性分析

本节给出了使用增广LKFs推导出的新稳定性准则.新型LKFs的形式如下：V=+=∑5k=1k+∑5k=1k，（6）

其中1=ξT1P1（d1（i））ξ1，2=1∑-d1m+1s=-d1MξT3（i+s，j）Q1（d1（i））ξ3（i+s，j），

3=1∑-1s=-d1M∑-1u=syT（i+u，j）Q3y（i+u，j），

4=∑-1s=-d1M∑-1u=s∑-1ν=uyT（i+ν，j）S1y（i+ν，j），5=∑-d1m-1s=-d1M∑-d1m-1u=s∑-1ν=uyT（i+ν，j）R1y（i+ν，j），

1=ξT2P2（d2（j））ξ2，2=2∑-d2m+1s=-d2MξT4（i，j+s）Q2（d2（j））ξ4（i，j+s），

3=2∑-1s=-d2M∑-1u=syT（i，j+u）Q4y（i，j+u），

4=∑-1s=-d2M∑-1u=s∑-1ν=uyT（i，j+ν）S2y（i，j+ν），5=∑-d2m-1s=-d2M∑-d2m-1u=s∑-1ν=uyT（i，j+ν）R2y（i，j+ν），

以及

ξ1（i，j）=［xT（i，j）  xT（i-d1（i），j）  ∑-1s=-d1m］xT（i+s，j）  ∑-1s=-d1m∑-1u=sxT（i+u，j）］T，

ξ2（i，j）=［xT（i，j）  xT（i，j-d2（i））  ∑-1s=-d2m］xT（i，j+s）  ∑-1s=-d2m∑-1u=sxT（i，j+u）］T，

ξ3（s，j）=［y（s，j）  x（s，j）  ∑-d1m-1u=sy（u，j）］T，ξ4（i，s）=［y（i，s）  x（i，s）  ∑-d2m-1u=sy（i，u）］T.

本文的創新之处是在创建LKFs（6）时，常数矩阵P1，P2和Q1，Q2被时滞相关矩阵P1（d1（i）），P2（d2（j））和Q1（d1（i）），Q2（d2（j））所替代，这些矩阵包含更多的时变时滞信息.另一方面，增广向量矩阵ξ1（i，j），ξ2（i，j），ξ3（i，j），ξ4（i，j）被添加到单项求和项中.受文献［24］中结果的启发，二次项中的时滞相关矩阵P1（d1（i）），P2（d2（j）），Q1（d1（i））和Q（d2（j））构造如下形式：P1（d1（i））=（d1M-d1（i））P111（i，0）+（d1（i）-d1m）P211（i，0）P12*P22，

P2（d2（j））=（d2M-d2（j））P111（0，j）+（d2（j）-d2m）P211（0，j）P12*P22，（7）

Q1（d1（i））=（d1（i）-d1m）Q111（i，0）+（d1M-d1（i））Q211（i，0）+Q10Q12*Q22，

Q2（d2（j））=（d2（j）-d2m）Q111（0，j）+（d2M-d2（j））Q211（0，j）+Q10Q12*Q22，（8）

需要以下表示以便推导出结果：

α1=d1（i）-d1m1，β1=d1M-d1（i）1，μ1=max｛|μ1m|，|μ1M|｝，a，b=1b-a+1∑-as=-bx（s，1），

α2=d2（j）-d2m2，β2=d2M-d2（j）2，μ2=max｛|μ2m|，|μ2M|｝，a，b=1b-a+1∑-as=-bx（1，s），

a，b=1（b-a+1）（b-a+2）∑-as=-b∑-au=sx（s，1），1=d1M-d1m，l=diag｛Rl，Rl，Rl｝，l=1，2，

a，b=1（b-a+1）（b-a+2）∑-as=-b∑-au=sx（1，s），2=d2M-d2m，k=diag｛Sk，Sk，Sk｝，k=1，2，

ei=［0n×（i-1）n  In  0n×（32-i）n］，i=1，2，…，32，es=A1eT1+A2eT2+A3deT3+A4deT4，

ζ=col｛x0，1，x1，0，x-d1（i），1，x1，-d2（j），x-d1m，1，x1，-d2m，x-d1M，1，x1，-d2M，x-d1m+1，1，x1，-d2m+1，x-d1M+1，1，x1，-d1M+1，

Δx-d1（i），1，Δx1，-d2（j），Δx0，1，Δx1，0，0，d1m，0，d2m，0，d1m，0，d2m，d1（i），d1M，d2（j），d2M，d1m，d1（i），d2m，d2（j），

d1（i），d1M，d2（j），d2M，d1m，d1（i），d2m，d2（j），0，d1M，0，d2M，0，d1M，0，d2M｝，

Π0=［eTs  eT3+eT13  （d1m+1）eT17-eT5  （d1m+1）（d1m+2）eT19-（d1m+1）eT5］T，ρ1=e9-e5，

Π3=［eTs  eT4+eT14  （d2m+1）eT18-eT6  （d2m+1）（d2m+2）eT20-（d1m+1）eT6］T，ρ2=e10-e6，

Π1=［eT1  eT3  （d1m+1）eT17-eT1  （d1m+1）（d1m+2）eT19-（d1m+1）eT1］T，ρ13=es-e1，

Π4=［eT2  eT4  （d2m+1）eT18-eT2  （d2m+1）（d2m+2）eT20-（d2m+1）eT2］T，ρ14=es-e2，

Π2=［eTs-eT1  eT13  eT1-eT5  （d1m+1）eT1-（d1m+1）eT5］T，Π7=［eT11-eT7  eT7  eT5-eT7］T，

Π5=［eTs-eT2  eT14  eT2-eT6  （d2m+1）eT2-（d2m+1）eT6］T，Π11=［eT12-eT8  eT8eT6-eT8］T，

Π9=［eT9-eT11  （d1M-d1（i）+1）eT21+（d1（i）-d1m+1）eT23-eT3-eT7  1eT5-（d1M-

d1（i）+1）eT21-（d1（i）-d1m+1）eT23+eT3+eT7］T，ρ15=［ρT5  ρT3］T，

Π13=［eT10-eT12  （d2M-d2（j）+1）eT22+（d2（j）-d1m+1）eT24-eT4-eT8  2eT6-（d2M-

d2（j）+1）eT22-（d2（j）-d1m+1）eT24+eT4+eT8］T，ρ16=［ρT6  ρT4］T，

ρ3=［eT3-eT7  3（eT3+eT7-2eT21）  5（eT3-eT7+6eT21-12eT25）］T，Π6=［eT9-eT5  eT5  0］T，

ρ4=［eT4-eT8  3（eT4+eT8-2eT22）  5（eT4-eT8+6eT22-12eT26）］T，Π10=［eT10-eT6  eT6  0］T，

ρ5=［eT5-eT3  3（eT5+eT3-2eT23）  5（eT5-eT3+6eT23-12eT27）］T，Π8=［0  0  eT9-eT5］T，

ρ6=［eT6-eT4  3（eT6+eT4-2eT24）  5（eT6-eT4+6eT24-12eT28）］T，Π12=［0  0  eT10-eT6］T，

ρ7=［2（eT1-eT29）  2（eT1+2eT29-6eT31）］T，ρ9=［2（eT3-eT21）  2（eT3+2eT21-6eT25）］T，

ρ8=［2（eT2-eT30）  2（eT2+2eT30-6eT32）］T，ρ10=［2（eT4-eT22）  2（eT4+2eT22-6eT26）］T，

ρ11=［2（eT5-eT23）  2（eT5+2eT23-6eT27）］T，ρ12=［2（eT6-eT24）  2（eT6+2eT24-6eT28）］T，

j11=diag｛j11，j11，j11｝，j=1，2，i=diag｛Ni，Ni，Ni｝，i=1，2，

θ1（Δd1（i））=1X1*1，Ξ1（Δd1（i））=111X3*111，Ξ2（Δd1（i））=211X4*211，

θ2（Δd2（j））=2X2*2，Ξ3（Δd2（j））=111X5*111，Ξ4（Δd2（j））=211X6*211.

以下定理是本文推導出的2-D离散时变时滞系统（1）的新稳定性准则.

定理1  系统（1）是渐近稳定的，如果存在4个4n×4n矩阵P111（Δd1（i））＞0，P211（Δd1（i））＞0，P111（Δd2（j））＞0，P211（Δd2（j））＞0，1个4n×2n矩阵P12，1个2n×2n矩阵P22＞0，5个n×n对称矩阵Q111（Δd1（i）），Q211（Δd1（i）），Q111（Δd2（j）），Q211（Δd2（j））和Q10，1个n×2n矩阵Q12，1个2n×2n矩阵满足Q22＞0，6个n×n矩阵Q3＞0，Q4＞0，S1＞0，S2＞0，R1＞0以及R2＞0，6个3n×3n对称矩阵X1，i=1，2，…，6，使得以下LMIs成立：1Pi11P12*P22＞0，1Qi11Q10Q12*Q22＞0，

2Pi11P12*P22＞0，2Qi11Q10Q12*Q22＞0，  i=1，2，（9）

N-1∶＝Q3-（μ1Q111（Δd1（i））+μ1Q211（Δd1（j）））＞0，N-2∶＝Q4-（μ2Q111（Δd2（i））+μ2Q211（Δd2（j）））＞0，（10）

1+1X1*10，111X3*1110，111X5*1110，

2+2X2*20，211X4*2110，211X6*2110，（11）

Ψ（Δd1（i），Δd2（j））＜0，（Δd1（i），Δd2（j））∈｛μ1m，μ1M｝×｛μ2m，μ2M｝，（12）

其中

Ψ（Δd1（i），Δd2（j））=Ψ1（Δd1（i），Δd2（j））-Ψ2（Δd1（i），Δd2（j）），

Ψ1（Δd1（i），Δd2（j））=ξT｛Δd1（i）∏T0（-P111+P211）∏0+Δd2（j）∏T3（-P111+P211）∏3+

∏T2P1∏2+1Δd1（i）ρT1（Q111-Q211）ρ1+1∏T6Q1（d1（i））∏6-2∏T11Q2（d2（j））∏11+

∏T5P2∏5+2Δd2（j）ρT2（Q111-Q211）ρ2+2∏T10Q2（d2（j））∏10-1∏T7Q1（d1（i））∏7+

21∏T8Q1（d1（i））∏8+22ρT14Q4ρ14+d1M（d1M+1）2ρT13S1Ρ13+d1（d1+1）2eT15R1e15+

22∏T12Q2（d2（j））∏12+21ρT12Q3ρ12+d2M（d2M+1）2ρT14S2ρ14+d2（d2+1）2eT16R2e16+

sym（∏T1P1∏2+∏T4P2∏5+1∏T9Q（d1（i））∏8+2∏T13Q（d2（j））∏13）｝ξ，

Ψ2（Δd1（i），Δd2（j））=ρT71ρ7+ρT82ρ8+ρT91ρ9+ρT102ρ10+ρT111ρ11+ρT122ρ12+

ρT15（Q1（Δd1（i））+（μ1-Δd1（i））Ξ1（Δd1（i））+（μ1+Δd1（i））Ξ2（Δd1（i））ρ15+

ρT16（Q2（Δd2（i））+（μ2-Δd2（i））Ξ3（Δd2（i））+（μ2+Δd2（i））Ξ4（Δd2（i））ρ16.

证明  考虑LKF（6）与4个时滞相关矩阵P1（d1（i）），P2（d2（j）），Q1（d1（i））和Q2（d2（j））被表示如式（7）和（8）.通过计算，矩阵P1（d1（i）），P2（d2（j）），P1（d1（i+1）），P2（d2（j+1）），Q1（d1（i）），Q2（d2（j）），Q1（d1（i+1））和Q2（d2（j+1））可重新表示如下：P1（d1（i））=11（d1M-d1（i））1P111（i，0）P12*P22+（d1（i）-d1m）1P211（i，0）P12*P22，

P2（d2（j））=12（d2M-d2（i））2P111（0，j）P12*P22+（d2（j）-d2m）2P211（0，j）P12*P22，

Q1（d1（i））=11（d1M-d1（i））1Q111（i，0）+Q10Q12*Q22+（d1（i）-d1m）1Q211（i，0）+Q10Q12*Q22，

Q2（d2（j））=12（d2M-d2（j））2Q111（0，j）+Q10Q12*Q22+（d2（j）-d2m）2Q211（0，j）+Q10Q12*Q22，（13）

P1（d1（i+1））=Δd1（i）（-P111（i，0）+P211（i，0））04n×2n04n×2n02n×2n+P1（d1（i）），

P2（d2（j+1））=Δd2（j）（-P111（0，j）+P211（0，j））04n×2n04n×2n02n×2n+P2（d2（j）），

Q1（d1（i+1））=Δd1（i）（Q111（i，0）-Q211（i，0））0n×2n02n×n02n×2n+Q1（d1（i）），

Q2（d2（j+1））=Δd2（j）（Q111（0，j）-Q211（0，j））0n×2n02n×n02n×2n+Q2（d2（j）），（14）

通過使用式（14）、（20）和（21），得到了P（d1（i））＞0，P（d2（j））＞0，Q1（d1（i））＞0和Q2（d2（j））＞0，这意味着存在一个正数λ1＞0，能够使得Vλ1‖x（i，j）‖2＞0，i=1，2，…，j=1，2，…，（15）

根据V作前向差分，ΔV（i，j）=V（i+1，j+1）-V（i，j），可得到：

Δ1=ζT｛Δd1（i）∏T0（-P111（i，0）+P211（i，0））∏0+∏T2P1∏2+sym（∏T1P1∏2）｝ζ，

Δ2=ζT｛1Δd1（i）ρT1（Q111-Q211）ρ1+1∏T6Q1（d1（i））∏6-1∏T7Q1（d1（i））∏7+

21∏T8Q1（d1（i））∏8+sym（1∏T9Q1（d1（i））∏8）｝ζ+

1Δd1（i）∑-d1ms=-d1M+1yT（s，1）（Q111（i，0）-Q211（i，0））y（s，1），

Δ3=21yT（0，1）Q3y（0，1）-1∑-d1m-1s=-d1MyT（s，1）Q3y（s，1），

Δ4=d1M（d1M+1）2yT（0，1）S1y（0，1）-∑-1s=-d1M∑-1u=syT（u，1）S1y（u，1），

Δ5=1（1+1）2yT（0，1）R1y（0，1）-∑-d1（i）-1s=-d1M∑-d1（i）-1u=syT（u，1）R1y（u，1）-

（d1M-d1（i））∑-d1m-1u=-d1（i）yT（u，1）R1y（u，1）-∑-d1m-1s=-d1（i）∑-d1m-1u=syT（u，1）R1y（u，1）.

使用類似的方法处理Δ，得到：

Δ1=ζT｛Δd2（j）∏T3（-P111（0，j）+P211（0，j））∏3+∏T5P2∏5+sym（∏T4P2∏5）｝ζ，

Δ2=ζT｛2Δd2（j）ρT2（Q111-Q211）ρ2+2∏T10Q2∏10-2∏T11Q2∏11+22∏T12Q2∏12+

sym（2∏T13Q2∏13）｝ζ+2Δd2（j）∑-d1m-1s=-d1M+1yT（1，s）（Q111（0，j）-Q211（0，j））y（1，s），

Δ3=22yT（1，0）Q4y（1，0）-2∑-d2m-1s=-d2MyT（1，s）Q4y（1，s），

Δ4=d2M（d2M+1）2yT（1，0）S2y（1，0）-∑-1s=-d2M∑-1u=syT（1，u）S2y（1，u），

Δ5=2（2+1）2yT（1，0）R2y（1，0）-∑-d2（j）-1s=-d2M∑-d2（j）-1u=syT（1，u）R2y（1，u）-

（d2M-d2（j））∑-d2m-1u=-d2（j）yT（1，u）R2y（1，u）-∑-d2m-1s=-d2（j）∑-d2m-1u=syT（1，u）R2y（1，u）.

根据N1∶＝Q3-（μ1Q111+μ1Q211），N2∶＝Q4-（μ2Q111+μ2Q211），Δ3，Δ3中的第2个积分项就可表示为：

-1∑-d1m-1s=-d1MyT（s，1）Q3y（s，1）=-1∑-d1（i）-1s=-d1MyT（s，1）N1y（s，1）-1∑-d1m-1s=-d1（i）yT（s，1）N1y（s，1）-

μ11∑-d1（i）-1s=-d1MyT（s，1）Q111y（s，1）-μ11∑-d1m-1s=-d1（i）yT（s，1）Q111y（s，1）-

μ11∑-d1（i）-1s=-d1MyT（s，1）Q211y（s，1）-μ11∑-d1m-1s=-d1（i）yT（s，1）Q211y（s，1），

-2∑-d2m-1s=-d2MyT（1，s）Q4y（1，s）=-2∑-d2（j）-1s=-d2MyT（1，s）N2y（1，s）-2∑-d2m-1s=-d2（j）yT（1，s）N2y（1，s）-

μ22∑-d2（j）-1s=-d2MyT（1，s）Q111y（1，s）-μ22∑-d2m-1s=-d2（j）yT（1，s）Q111y（1，s）-

μ22∑-d2（j）-1s=-d2MyT（1，s）Q211y（1，s）-μ22∑-d2m-1s=-d2（j）yT（1，s）Q211y（1，s）.

因此，就得到：

ΔV=ζTΨ1［Δd1（i），Δd2（j）］ζ-1∑-d1（i）-1s=-d1MyT（s，1）N1y（s，1）-2∑-d2（j）-1s=-d2MyT（1，s）N2y（1，s）-

1∑-d1m-1s=-d1（i）yT（s，1）N1y（s，1）-1（μ1-Δd1（i））∑-d1（i）-1s=-d1MyT（s，1）Q111y（1，s）-

2∑-d2m-1s=-d2（j）yT（1，s）N2y（1，s）-1（μ1-Δd1（i））∑-d1m-1s=-d1（i）yT（s，1）Q111y（s，1）-

1（μ1+Δd1（i））∑-d1（i）-1s=-d1MyT（s，1）Q211y（s，1）-（d2M-d2（j））∑-d2m-1s=-d2（j）yT（1，s）R2y（1，s）-

2（μ2-Δd2（j））∑-d2（j）-1s=-d2MyT（1，s）Q111y（1，s）-（d1M-d1（i））∑-d1m-1s=-d1（i）yT（s，1）R1y（s，1）-

2（μ2+Δd2（j））∑-d2m-1s=-d2（j）yT（1，s）Q211y（1，s）-∑-1s=-d2M∑-1u=syT（1，u）S2y（1，u）-

2（μ2+Δd2（j））∑-d2（j）-1s=-d2MyT（1，s）Q211y（1，s）-∑-1s=-d1M∑-1u=syT（u，1）S1y（u，1）-

∑-d1（i）-1s=-d1M∑-d1（i）-1u=syT（u，1）R1y（u，1）-1（μ1+Δd1（i））∑-d1m-1s=-d1（i）yT（s，1）Q211y（s，1）-

∑-d2（j）-1s=-d2M∑-d2（j）-1u=syT（1，u）R2y（1，u）-2（μ2+Δd2（j））∑-d2m-1s=-d2（j）yT（1，s）Q111y（1，s）-

∑-d1m-1s=-d1（i）∑-d1m-1u=syT（u，1）R1y（u，1）-∑-d2m-1s=-d2（j）∑-d2m-1u=syT（1，u）R2y（1，u）.

由于Q111（i，0）＞0，Q211（i，0）＞0，Q111（0，j）＞0，Si＞0，Ri＞0，i=1，2和N1＞0，N2＞0，通過使用α1，α2，β1，β2，可得到：-1∑-d1m-1s=-d1（i）yT（s，1）N1y（s，1）-1α1ζT｛ρT51ρ5｝ζ，

-2∑-d2m-1s=-d2（j）yT（1，s）N2y（1，s）-1α2ζT｛ρT62ρ6｝ζ，

-1∑-d1（i）-1s=-d1MyT（s，1）N1y（s，1）-1β1ζT｛ρT31ρ3｝ζ，

-2∑-d2（j）-1s=-d2MyT（1，s）N2y（1，s）-1β2ζT｛ρT42ρ4｝ζ，

∑-1s=-d1M∑-1u=syT（u，1）S1y（u，1）ζT｛-ρT71ρ7｝ζ，

∑-1s=-d2M∑-1u=syT（1，u）S1y（1，u）ζT｛-ρT82ρ8｝ζ，

∑-d1（i）-1s=-d1M∑-d1（i）-1u=syT（u，1）R1y（u，1）ζT｛-ρT91ρ9｝ζ，

∑-d2（j）-1s=-d2M∑-d2（j）-1u=syT（1，u）R2y（1，u）ζT｛-ρT102ρ10｝ζ，

∑-d1m-1s=-d1（i）∑-d1m-1u=syT（u，1）R1y（u，1）ζT｛-ρT111ρ11｝ζ，

∑-d2m-1s=-d2（j）∑-d2m-1u=syT（1，u）R2y（1，u）ζT｛-ρT122ρ12｝ζ，

-（d1M-d1（i））∑-d1m-1s=-d1（i）yT（s，1）R1y（s，1）-（1α1-1）ζT｛ρT51ρ5｝ζ，

-（d2M-d2（j））∑-d2m-1s=-d2（j）yT（1，s）R2y（1，s）-（1α2-1）ζT｛ρT62ρ6｝ζ，

-1（μ1-Δd1（i））∑-d1（i）-1s=-d1MyT（s，1）Q111y（s，1）-（μ1-Δd1（i））1β1ζT｛ρT3111ρ3｝ζ，

-1（μ1+Δd1（i））∑-d1（i）-1s=-d1MyT（s，1）Q211y（s，1）-（μ1+Δd1（i））1β1ζT｛ρT3211ρ3｝ζ，

-2（μ2-Δd2（j））∑-d2（j）-1s=-d2MyT（1，s）Q111y（1，s）-（μ2-Δd2（j））1β2ζT｛ρT4111ρ4｝ζ，

-1（μ1+Δd1（i））∑-d1m-1s=-d1（i）yT（s，1）Q111y（s，1）-（μ1-Δd1（i））1α1ζT｛ρT5111ρ5｝ζ，

-1（μ1-Δd1（i））∑-d1m-1s=-d1（i）yT（s，1）Q211y（s，1）-（μ1+Δd1（i））1α1ζT｛ρT5211ρ5｝ζ，

-2（μ2-Δd2（j））∑-d2m-1s=-d2（j）yT（1，s）Q111y（1，s）-（μ2-Δd2（j））1α2ζT｛ρT6111ρ6｝ζ，

-2（μ2+Δd2（j））∑-d2m-1s=-d2（j）yT（1，s）Q211y（1，s）-（μ2+Δd2（j））1α2ζT｛ρT6211ρ6｝ζ，

-2（μ2+Δd2（j））∑-d2（j）-1s=-d2MyT（1，s）Q211y（1，s）-（μ2+Δd2（j））1β2ζT｛ρT4211ρ4｝ζ，

根据（10）和（11），通过使用引理2，就可得到以下6个估计不等式：

-1α1ζT｛ρT51ρ5｝ζ-1β1ζT｛ρT31ρ3｝ζ-（1α1-1）ζT｛ρT51ρ5｝ζζT｛-ρT15θ1ρ15｝ζ，

-1α2ζT｛ρT62ρ6｝ζ-1β2ζT｛ρT42ρ4｝ζ-（1α2-1）ζT｛ρT62ρ6｝ζζT｛-ρT16θ2ρ16｝ζ，

-（μ1-Δd1（i））ζT｛1α1ρT5111（i，0）ρ5+1β1ρT3111（i，0）ρ3｝ζζT｛-ρT15Ξ1ρ15｝ζ，

-（μ1+Δd1（i））ζT｛1α1ρT5211（i，0）ρ5+1β1ρT3211（i，0）ρ3｝ζζT｛-ρT15Ξ2ρ15｝ζ，

-（μ2-Δd2（j））ζT｛1α2ρT6111（0，j）ρ6+1β2ρT4111（0，j）ρ4｝ζζT｛-ρT16Ξ3ρ16｝ζ，

-（μ2+Δd2（j））ζT｛1α2ρT6211（0，j）ρ6+1β2ρT4211（0，j）ρ4｝ζζT｛-ρT16Ξ4ρ16｝ζ，（16）

综上所述，就获得VζTΨ（d1（i），d2（j））ζ.证明系统是渐近稳定的，证毕.

推论1  对于LKFs（6）不使用时滞相关矩阵的情况，通过设置P111=P211和Q111=Q211=0，即4个矩阵P1（d1（i）），P2（d2（j）），Q1（d1（i））和Q2（d2（j））被简化为4个常数矩阵P1，P2，Q1和Q2，根据定理1，就得到不使用时滞相关矩阵的系统稳定性准则：系统是渐近稳定的，如果存在2个6n×6n矩阵Pi=iP111P12*P22＞0，i=1，2，2个3n×3n矩阵Qi=Q10Q12*Q22＞0，i=1，2，6个n×n矩阵Q3＞0，Q4＞0，S1＞0，S2＞0，R1＞0，R2＞0，2个3n×3n对称矩阵X1，X2，使得以下LMIs（9）和（10）满足Q111=Q211=0，并且Q1（d1（i）），Q2（d2（j））被Q1，Q2替代，N1，N2被Q3，Q4所替代.

注1  当μ1m，μ2m，μ1M，μ2M，d1m，d2m，d1M和d2M的值固定时，定理1和推论1中的稳定性条件将更改为LMIs.通过使用MATLAB工具最大化时变时滞的算法，对于固定值，就可以获得最大时变时滞的上界d2M的值，即时滞范围.

3  數值算例

在本节中，提出了两个数值算例，一个选择没有使用时滞相关矩阵，另一个则使用，以验证本文所提出稳定性准则的有效性.

例1  化学反应器、热交换器或管式炉中的热过程可以用以下具有时滞的局部可微分方程来表示［6］：

T（x，t）x=T（x，t）t-a（x，t，T（x，t））T（x，t）-b（x，t，T（x，t））T（x，t-τ1），

其中T（x，t）是空间x和时间t处的温度，τt是时滞，a（·）=a（x，t，T（x，t）），b（·）=b（x，t，T（x，t））是系数函数，具体取决于状态T（x，t）.倘若

T（i，j）=T（iΔx，jΔt），T（x，t）x≈T（i，j）-T（i-1，j）Δx，T（x，t）t≈T（i，j+1）-T（i，j）Δx.

下列2-D线性模型就可以得到：T（i，j+1）=（1-ΔtΔx-a0Δt）T（i，j）+ΔtΔxT（i-1，j）-a1ΔtT（i，j-d2）+bΔtu（i，j）.

记xT（i，j）=［TT（i-1，j）TT（i，j）］，这样2-D FM模型就可以转化为：x（i+1，j+1）=A1x（i，j+1）+A2x（i+1，j）+A1dx（i-d1（i），j+1）+A2dx（i+1，j-d2（j）），其中

A1=00ΔtΔx1-ΔtΔx-a0Δt，A2=0100，A1d=000-a1Δt，A2d=0000.

令Δt=0.1，Δx=0.4，a0=1，a1=1.2，b=1将上述参数代入矩阵.考虑具有以下系统矩阵和参数的2-D离散时滞系统（1）［28］（不使用时滞相关矩阵）：

A1=000.250.65A2=0100A1d=000-0.12A2d=0000.（17）

当时滞d2（j）对于d1（i）=6+5sin（πi/2）具有时变性时，文献［32］中的系统对于0d2（j）13是渐近稳定的，即d2（j）的上界远大于文献［6］中给出的上界.此外，对于推论1，系统在满足0d2（j）20下仍然是渐近稳定的，这表明时滞上界大于文献［32］中给出的.表1中列出了允许的最大上界.从表1中，可以看到推论1提供了最大的允许上界.图1和图2显示了系统两个状态变量在任意（随机生成）边界条件下的轨迹.

图1和图2显示，随着i和j继续增加，状态振幅变小并最终接近原点，即具有系数矩阵（17）的系统（1）在时滞上界d2M=48下渐近稳定.

例2  研究了具有以下参数的2-D系统（1）（使用时滞相关矩阵）［33］：

A1=0.1000.2A2=0.400.20A1d=0.02000.01A2d=0.01000.01.（18）

假设时变时滞满足条件：μ1M=-μ1m=μ2M=-μ1M=μ1M=μ和条件（2）.将文献［29］中的结果与本文中的LMIs决策变量数目进行比较，由表2，本文决策变量的数目小于文献［29］定理1中的数量.为了比较时滞范围，对比文献［27-29，34-35］的定理1以及本文结论可以找到最大允许上界d2M，并在表3中列出，且有：1）本文定理1得到的最大允许上界大于推论1中的，这表明本文设计的在单项求和项中引入时滞相关矩阵对于推导稳定性准则非常有意义；2）本文定理1和推论1中获得的最大允许上界大于文献［29］中获得的，这证实了本文推导的结果优于其他参考文献获得的结果.综上，本文获得的结果比参考文献的保守性更小.

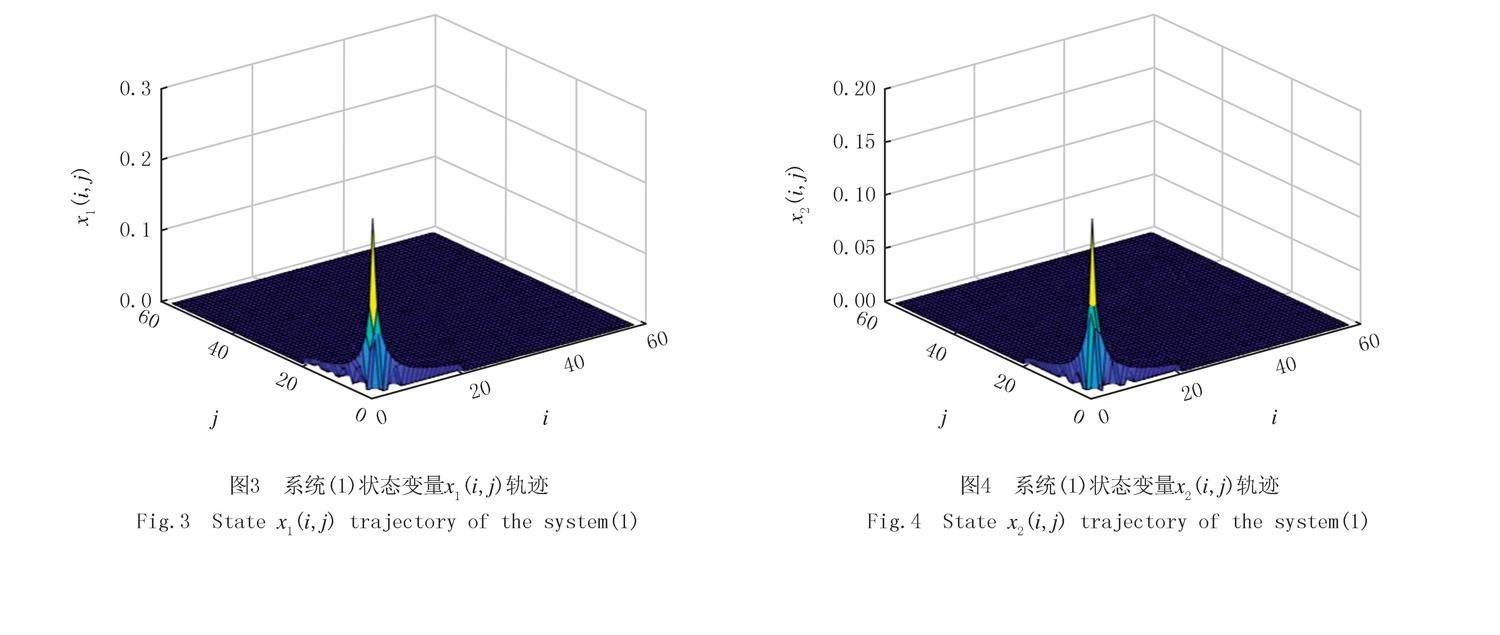
系统的两个状态变量在任意（随机生成）边界条件下的轨迹如图3和图4所示.在初始状态下，状态波动一开始变化显著，随着i和j的增加，系统状态逐渐接近于零，因此本文给出的系统稳定性准则被证明是有效且有意义的.这也为以后设置控制器奠定了坚实的基础.

4  结  论

本文创建具有三重求和项的LKFs同时考虑了时滞相关矩阵和增广向量矩阵，包含有关时滞上界和下界的更多信息.然后利用多重辅助函数不等式和互凸组合不等式获得了新的系统稳定性准则，扩大了时滞范围并降低了结果的保守性.同时本文结果减少了决策变量的数目，从而减轻了计算负担.最后，通过数值算例与现有结果进行对比，验证了本文所设计方法的有效性和优越性.本文设计的增广向量矩阵中可同时包含时滞的上界和下界，并以此用来估计双重求和项中的系统LKFs差分过程，进一步降低稳定性准则的保守性，但会加大差分难度和计算量，进而怎么处理LKFs差分产生的有限和项，值得学者们进一步探索.

参  考  文  献

［1］   WU L G，WANG Z D，GAO H J，et al.Filtering for uncertain 2-D discrete systems with state delays［J］.Signal Processing，2007，87（9）：2213-2230.

［2］BISTRITZ Y.On testing stability of 2-D discrete systems by a finite collection of 1-D stability tests［J］.IEEE Transactions on Circuits and Systems I：Fundamental Theory and Applications，2002，49（11）：1634-1638.

［3］KAR H，SINGH V.Robust stability of 2-D discrete systems described by the Fornasini-Marchesini second model employing quantization/overflow nonlinearities［J］.IEEE Transactions on Circuits and Systems II：Express Briefs，2004，51（11）：598-602.

［4］HUA M G，DENG F Q，LIU X Z，et al.Robust delay-dependent exponential stability of uncertain stochastic system with time-varying delay［J］.Circuits，Systems and Signal Processing，2010，29（3）：515-526.

［5］LI Z，LIU H，GAO H.A delay partitioning approach tofiltering for continuous time-delay systems［J］.Circuits Systems and Signal Process，2011，30（3）：501-513.

［6］XU J M，YU L.Delay-dependent H∞ control for 2-D discrete state delay systems in the second FM model［J］.Multidimensional Systems and Signal Processing，2009，20（4）：333-349.

［7］PENG D，GUAN X P，LONG C N.Robust output feedback guaranteed cost control for 2-d uncertain state-delayed systems［J］.Asian Journal of Control，2007，9（4）：470-474.

［8］PENG D，GUAN X P.Output feedback H∞ control for 2-D state-delayed systems［J］.Circuits，Systems & Signal Processing，2009，28（1）：147-167.

［9］KWON O M，PARK M J，PARK J H，et al.Improved delay-dependent stability criteria for discrete-time systems with time-varying delays［J］.Circuits，Systems，and Signal Processing，2013，32（4）：1949-1962.

［10］CHEN Q，LIU X G，WANG F X.Improved results on-state estimation for neural networks with time-varying delay［J］.Circuits，Systems，and Signal Processing，2022，41（1）：122-146.

［11］SHAHBAZZADEH M，SADATI S J.Delay-dependent stabilization of time-delay systems with nonlinear perturbations［J］.Circuits，Systems，and Signal Processing，2022，41（2）：684-699.

［12］VAN HIEN L，TRINH H.Stability of two-dimensional Roesser systems with time-varying delays via novel 2D finite-sum inequalities［J］.IET Control Theory & Applications，2016，10（14）：1665-1674.

［13］PARK P，LEE W I，LEE S Y.Auxiliary function-based integral/summation inequalities：application to continuous/discrete time-delay systems［J］.International Journal of Control，Automation and Systems，2016，14（1）：3-11.

［14］LEE S Y，LEE W I，PARK P.Polynomials-based summation inequalities and their applications to discrete-time systems with time-varying delays［J］.International Journal of Robust and Nonlinear Control，2017，27（17）：3604-3619.

［15］GHOLAMI H，BINAZADEH T.Fixed-time control of nonlinear discrete-time systems with time-varying delay and uncertain parameters：state and output feedback approaches［J］.Soft Computing，2021，25（17）：11509-11522.

［16］FRIDMAN E，SHAKED U，LIU K.New conditions for delay-derivative-dependent stability［J］.Automatica，2009，45（11）：2723-2727.

［17］KWON O M，PARK M J，PARK J H，et al.Stability and stabilization for discrete-time systems with time-varying delays via augmented Lyapunov-Krasovskii functional［J］.Journal of the Franklin Institute，2013，350（3）：521-540.

［18］SEURET A，GOUAISBAUT F，FRIDMAN E.Stability of discrete-time systems with time-varying delays via a novel summation inequality［J］.IEEE Transactions on Automatic Control，2015，60（10）：2740-2745.

［19］ZENG H B，HE Y，WU M，et al.Free-matrix-based integral inequality for stability analysis of systems with time-varying delay［J］.IEEE Transactions on Automatic Control，2015，60（10）：2768-2772.

［20］JIN P M，HOON L S，MIN K O，et al.Augmented Lyapunov-krasovskii functional approach to stability of discrete systems with time-varying delays［J］.IEEE Access，2017，5：24389-24400.

［21］ZHANG C K，HE Y，JIANG L，et al.Delay-variation-dependent stability of delayed discrete-time systems［J］.IEEE Transactions on Automatic Control，2016，61（9）：2663-2669.

［22］CHEN J，XU S Y，MA Q，et al.Two novel general summation inequalities to discrete-time systems with time-varying delay［J］.Journal of the Franklin Institute，2017，354（13）：5537-5558.

［23］KWON W，KOO B，LEE S M.Novel Lyapunov-Krasovskii functional with delay-dependent matrix for stability of time-varying delay systems［J］.Applied Mathematics and Computation，2018，320：149-157.

［24］NAM P T，LUU T H.A new delay-variation-dependent stability criterion for delayed discrete-time systems［J］.Journal of the Franklin Institute，2020，357（11）：6951-6967.

［25］SOLGI Y，FATEHI A，SHARIATI A.Non-monotonic Lyapunov-Krasovskii functional approach to stability analysis and stabilization of discrete time-delay systems［J］.IEEE/CAA Journal of Automatica Sinica，2020，7（3）：752-763.

［26］YANG R N，LI L L.Observer-based finite-region dissipative control for 2-D continuous-discrete systems over networks［J］.Journal of the Franklin Institute，2020，357（16）：11974-11995.

［27］PENG D，ZHANG J，HUA C C，et al.A delay-partitioning approach to the stability analysis of 2-D linear discrete-time systems with interval time-varying delays［J］.International Journal of Control，Automation and Systems，2018，16（2）：682-688.

［28］PENG D，HUA C C.Delay-dependent stability and static output feedback control of 2-D discrete systems with interval time-varying delays［J］.Asian Journal of Control，2014，16（6）：1726-1734.

［29］PENG D，XU H S.A novel approach to delay-variation-dependent stability analysis of 2-D discrete-time systems with mixed delays［J］.IEEE Access，2019，7：99817-99829.

［30］NAM P T，TRINH H，PATHIRANA P N.Discrete inequalities based on multiple auxiliary functions and their applications to stability analysis of time-delay systems［J］.Journal of the Franklin Institute，2015，352（12）：5810-5831.

［31］SEURET A，GOUAISBAUT F.Allowable delay sets for the stability analysis of linear time-varying delay systems using a delay-dependent reciprocally convex lemma［J］.IFAC-PapersOnLine，2017，50（1）：1275-1280.

［32］FENG Z Y，HE Y，XU L，et al.Delay-dependent robust stability and stabilisation of uncertain two-dimensional discrete systems with time-varying delays［J］.IET Control Theory & Applications，2010，4（10）：1959-1971.

［33］YAO J，WANG W Q，ZOU Y.The delay-range-dependent robust stability analysis for 2-D state-delayed systems with uncertainty［J］.Multidimensional Systems and Signal Processing，2013，24（1）：87-103.

［34］PENG D，HUA C C.Improved approach to delay-dependent stability and stabilisation of two-dimensional discrete-time systems with interval time-varying delays［J］.IET Control Theory & Applications，2015，9（12）：1839-1845.

［35］ZHANG J，PENG D，HUA C C，et al.New approach to delay-dependent stability of two-dimensional discrete-time systems with interval time-varying delays［C］//2017 29th Chinese Control and Decision Conference（CCDC）.［s.l.］：IEEE，2017：5604-5609.

New delay-variation-dependent stability criterion for 2-D discrete systems with delays

Peng Dan， Zhang Mingxia

（School of Science， Yanshan University， Qinhuangdao 066004， China）

Abstract： The delay-variation-dependent stability problem for two-dimensional（2-D） discrete-time systems with delays is studied. The Lyapunov-Krasovskii functionals（LKFs） are constructed by using delay-dependent matrices in the quadratic and single-sum terms， respectively， considering more state information. It is also the first time that the augmented vector matrices in the single summation term have been studied the system stability. Meanwhile， the multiple auxiliary function inequality and reciprocally convex inequality suitable for 2-D systems are given to process LKFs differentiation so as to reduce the computational burden. Derive a less conservative stability criterion for 2-D discrete systems with time-varying delays. The effectiveness and superiority of the devised method is confirmed by two numerical examples.

Keywords： two-dimensional discrete systems; time-varying delays; Lyapunov-Krasovskii functionals; multiple auxiliary function inequality; reciprocally convex inequality

［責任编校  陈留院  赵晓华］