土与强风化岩双元边坡圆弧-平面破坏模式与支护设计方法

李连祥 贾斌 赵忠杨 韩志霄 李胜群

摘要：为了探究土与强风化岩边坡中强风化岩不破坏的临界坡率及稳定性判断方法，基于濟南地层，得出适用于数值模拟的土层参数，并利用强度折减法求出边坡的临界坡率，为施工提供参考。针对强风化岩不破坏的边坡，运用改进的瑞典条分法求出边坡安全系数解析解，并利用滑移线场法求出滑移线，为安全系数解析解的应用提供依据。结果表明，岩层厚度超过边坡高度1/2或坡率大于1：0.5时，强风化岩一定破坏；解析解得出的安全系数偏小，有利于工程安全；针对土与强风化岩边坡，文中结果可确定边坡破坏区域，设计支护方案。

关键词：边坡稳定；安全系数；土岩双元边坡；瑞典条分法；滑移线场法；解析解

中图分类号：U416.1+4          文献标志码：A      文章编号：1000-582X（2024）02-001-13

Arc-plane failure mode and support design method of dual-element slope of soil and strongly weathered rock

LI Lianxiang1a， 1b， JIA Bin1a， 1b， ZHAO Zhongyang2， HAN Zhixiao1a， 1b， LI Shengqun1a， 1b

（1a. Foundation Pit and Deep Foundation Engineering Research Center; 1b. School of Civil Engineering， Shandong University， Jinan 250061， P. R. China; 2. First Construction Co.， Ltd.， China Construction Eighth Bureau， Jinan 250014， P. R. China）

Abstract： To investigate the non-destructive critical slope rate and stability assessment method for strongly weathered rock slopes with soil and highly weathered rock， based on Jinans strata， suitable soil layer parameters for numerical simulation are determined. The strength reduction method is then applied to calculate the critical slope rate of the slope， providing reference for construction. The analytical solution for the slopes safety factor is obtained using the improved Swedish slice method and the slip line field method. These analytical solutions provide essential prerequisties for safety factor applications. Results show that strongly weathered rock experiences failure when the rock strata thickness exceeds half of the slope height or the slope ratio surpasses 1：0.5. The obtained safety factor from the analytical solution tends to be conservative， contributing to enhanced engineering safety. For soil and strongly weathered rock slope， the research findings help identify the failure area， facilitating the design of support schemes.

Keywords： slope stability; hazard index; soil rock double slope; Swedish division; slip line field method; analytical solution

在基坑和边坡工程中，出现了大量上层土体+下部岩体的双元边坡。以山东省济南市为例，市区地层主要由第四系土体、灰岩、辉长岩3种岩土体组成[1?2]。市区基坑开挖深度范围大致在6～30 m之间。土岩双元基坑边坡岩土层分布情况可分为4类[1]：1）土+全风化辉长岩；2）土+全风化辉长岩+强风化辉长岩；3）土+全风化辉长岩石+强风化辉长岩+中风辉长化岩；4）土+中风化灰岩。目前，基坑土体边坡[3]整体稳定分析明确按圆弧滑动模式，建筑岩质边坡[4]建议按外倾结构面分析。对于土与全风化岩边坡，可以将全风化岩当作土层分析[3]，按建筑基坑支护技术规程[4]进行边坡设计；对于土与强风化岩边坡的整体稳定性分析均缺乏明确规定[5]，大量土岩双元边坡仍按圆弧滑动法为基础的商用软件验算，与已有文献出现较大差异[6?7]。因此，研究土与强风化岩双元边坡破坏模式具有重要的理论意义和工程价值。

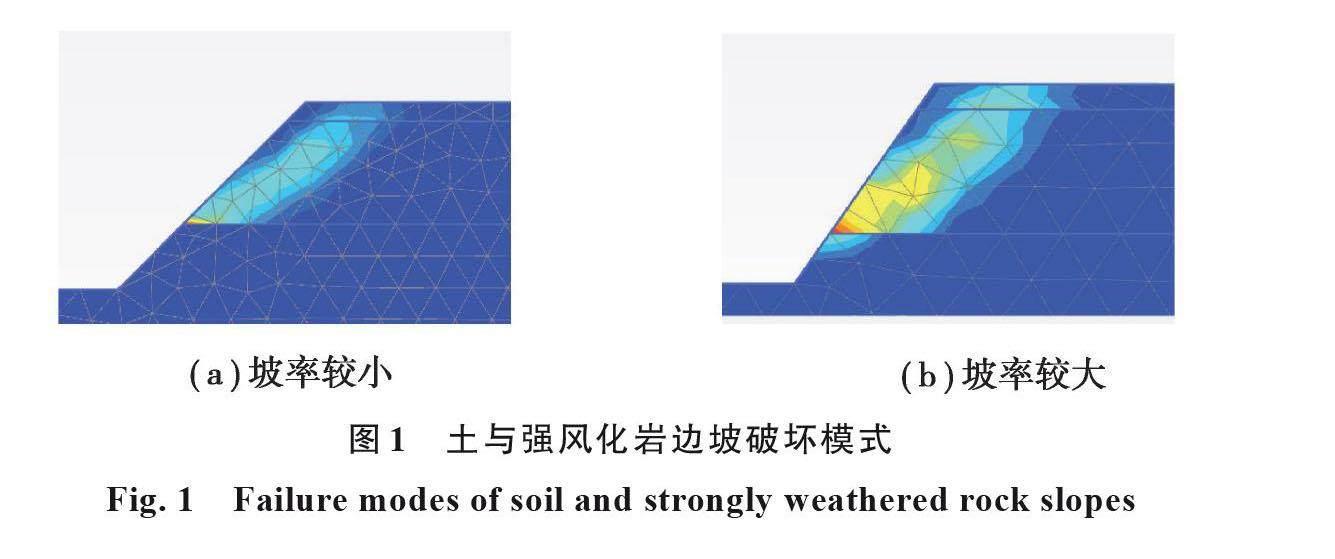
笔者前期研究表明，土与强风化岩双元边坡坡率较小时，破坏模式为圆弧-平面滑动破坏模式，强风化岩层不发生破坏，如图1（a）所示；坡率较大时，破坏模式为圆弧-平面-局部破坏体破坏模式，如图1（b）所示；尚不能成为工程依据，明确强风化岩破坏的规律具有紧迫性。

目前，求安全系数的方法主要是瑞典条分法，对单一边坡[8?10]进行水平条分或竖直条分，忽略土条条间力作用，分别得到水平积分模型和竖直积分模型的安全系数解析解[11?12]。有学者对瑞典条分法做出了一些改进，将起伏不平的坡面简化为分段直线进行积分[13?17]，假设土条间只有水平推力等[14]，主体思想仍然是滑动面为圆弧面[15?16]。但瑞典条分法有一个前提条件，需指定滑动面。对于潜在滑移线（面）的确定，已有学者认为滑移线场法具有更重要的意义。滑移线场法根据弹塑性有限元的应力分析结果[17?19]，用数值积分方法得出边坡潜在滑移线（面）[20?23]， 最危险潜在滑移线和边坡稳定性安全系数[24?25]，是确定岩土潜在滑移线的通用方法。当岩土应力达到破坏状态时，确定的潜在滑移线将转为真正的滑移线[26]。但现有研究仅在理论层面推进滑移线场法，缺乏实际工程应用。

文中基于济南地质条件的土与强风化岩双元边坡，采用数值模拟获得强风化岩破坏体出现的临界坡率，针对强风化岩不发生破坏的边坡，推导出边坡安全系数解析解，进一步根据滑移线场法求出潜在滑移线的位置。最后结合实际案例，运用深基坑软件设计支护方案，为文中方法在工程上的应用提供参考。

1 数值模型建立

1.1 数值模型

深基坑工程数值模拟采用土体小应变强化模型（HSS）具有科学性。其需要的重度γ、黏聚力c、内摩擦角?等参数可由勘察报告获得，但模型所需的E_oed^ref、E_50^ref、E_ur^ref勘察报告没有提供，只能通过位移反分析技术获得[27?29]。首先给定参数初值，通过有限元程序进行正演及逐次修正预调参数取值，以逼近实测结果。文中选取济南传媒大厦地层，结合PLAXIS手册推荐，进行参数初选时，各土层中E_ur^ref：E_50^ref：E_oed^ref：E_S^（1-2）取3∶1∶1∶1。各地层参数及HSS模型参数初值如表1所示。基坑开挖及支护施工工况如表2所示。模型尺寸为80 m×50 m×20 m，平臺长12 m，边界条件为底面提供全约束，相当于固定支座，四周提供法向约束，相当于滑动铰支 座，顶部自由。数值模型如图2所示。

1.2 参数确定

坡顶的沉降是边坡监测中较为重要的变形，因此，本次参数反演所选位移为边坡坡顶沉降。参数反演终止条件为

W=Δz/（2z_max ）+Δx/2X ， （1）

式中：W为终止条件；△z为数值计算与实测数据沉降最大值之差；zmax为边坡实测最大沉降；△x为数值计算与实测数据坡顶沉降出现最大水平位移的位置差；X为坡顶监测长度。

以工况6进行参数反演，参数调整幅值控制在10%以内。终止条件为W≤20%，可满足工程需要。限于文章篇幅，参数反分析过程省略，结果如表3所示。

图3为参数反演结束时坡顶沉降数值计算结果与实测值的对比。数值计算结果与实测值基本吻合，最大沉降分别为56.54 mm和54.41 mm。为确定表3参数选取的准确性，需选择后续工况进行验证。图4为工况9时，坡顶沉降数值计算与实测对比。数值计算结果与实测数据再次吻合较好，验证了参数选取的准确性。证明以此参数为基础研究土岩双元边坡所获得结果具有科学性。

2 强风化岩是否破坏的临界坡率

对于上层为土与全风化岩石，下层为强风化岩石的边坡，当坡率不同时，边坡破坏模式不同，如果确定强风化岩不会破坏，就可以免去强风化岩的锚杆支护。基于上述经过验证的数值模型，探究不同边坡高度强风化岩不同厚度时破坏体出现的临界坡率。

大部分基坑开挖深度位于10～25 m范围内[3]，文中选取开挖深度分别为12、16、20、24 m，研究对应临界坡率。为便于研究，土层参数由表3中3种土层按厚度进行加权平均，计算参数如表4所示。全风化岩石及强风化岩石的参数根据表1取得。由于边坡高度及强风化岩层厚度不断变化，为便于分析，土层设定为边坡高度的1/3，全风化岩层厚度随强风化岩层变化而变化。

2.1 研究方法

模型设计参照图2所示，按照不同的开挖深度调整模型的深度。为减少无关变量影响，模型采用放坡开挖，每一步开挖2 m，直到开挖到底，进行安全性计算。取边坡高度、强风化岩厚度为自变量，强风化岩破坏体出现的临界坡率为因变量。

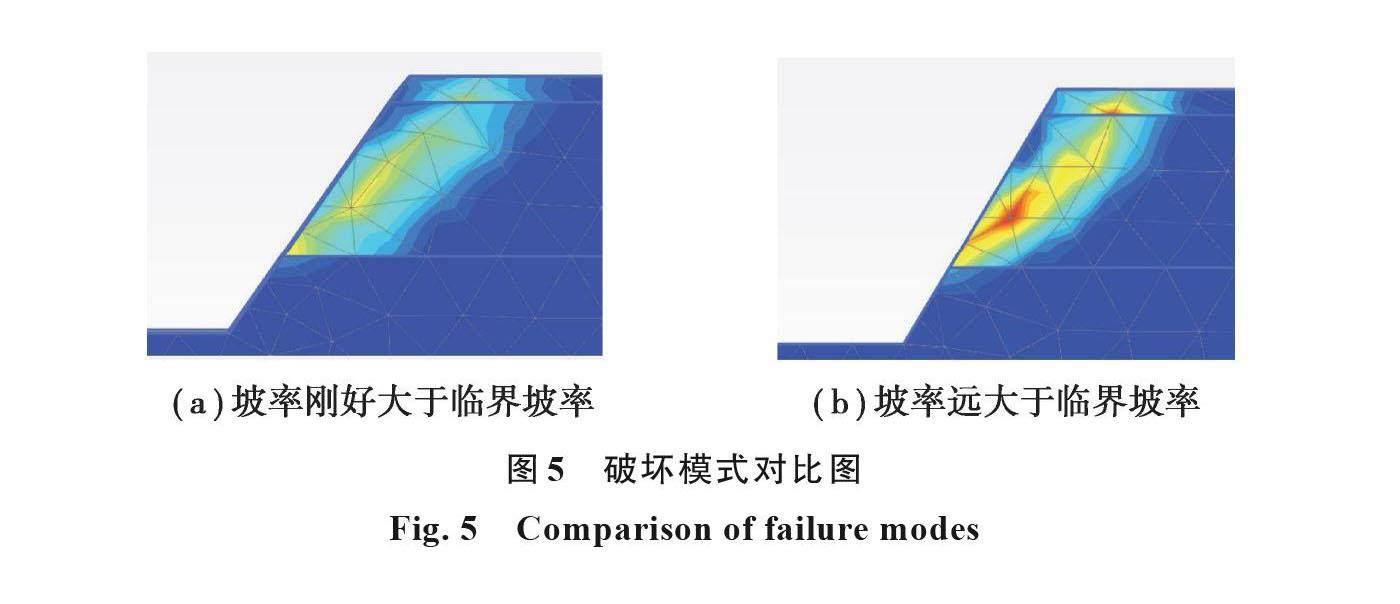
针对同一边坡高度及强风化岩厚度占比，不断变化坡率，进行边坡稳定性计算。在计算过程中发现，岩体破坏时出现2种破坏模式，如图5所示。图5（a）为坡率刚好大于临界坡率时的边坡破坏模式，图5（b）为坡率比临界坡率大较多时的边坡破坏模式。可以看出，左侧图片中的岩体只破坏了一小部分，右侧图片的岩体破坏面已经和上面的土层贯通，说明当坡率逐渐大于临界坡率时，土层给岩层的剪切力逐渐增大，岩体破坏范围也逐渐扩大。

2.2 临界坡率分析

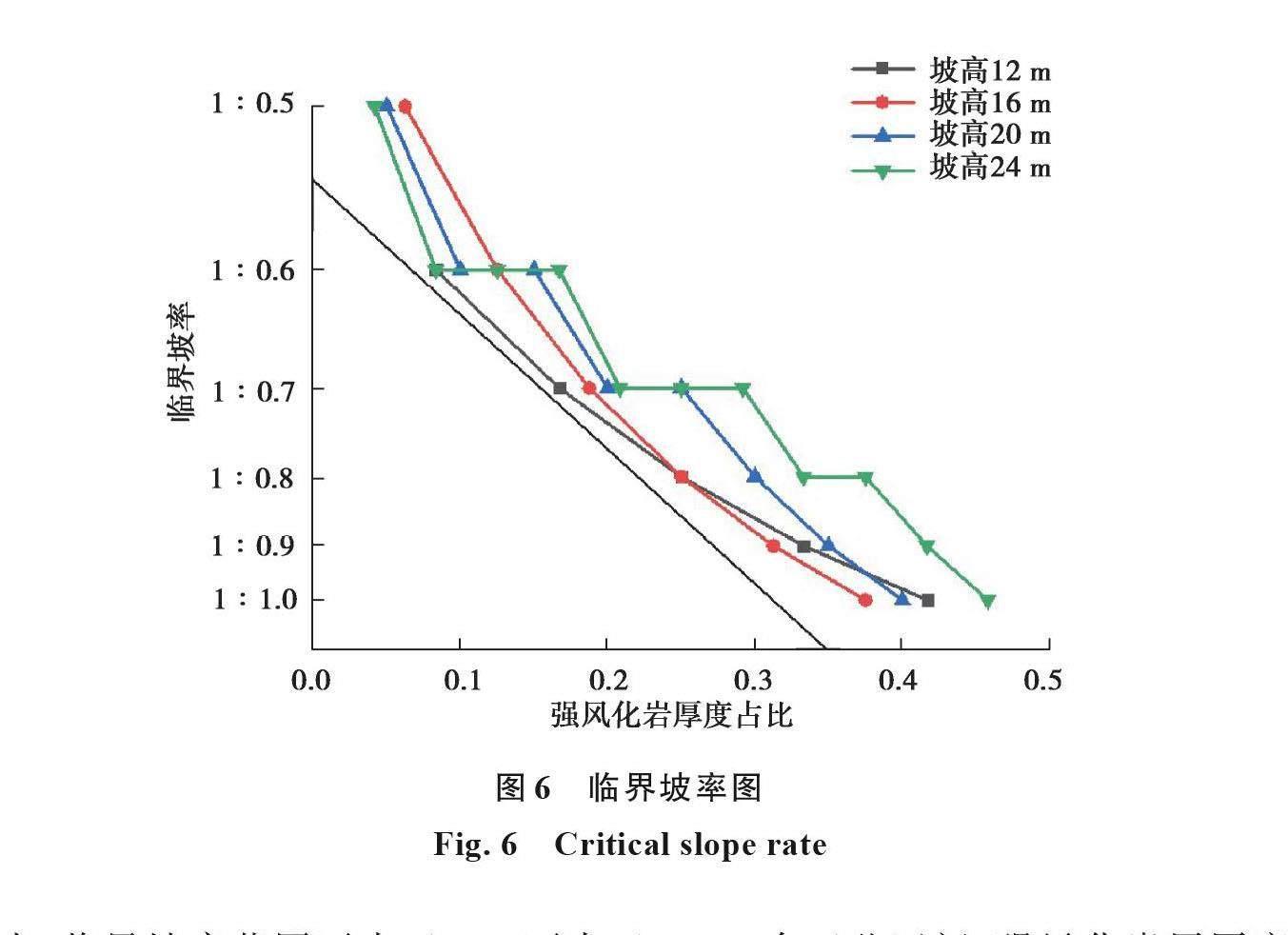
所有模型计算完成之后，提取不同边坡高度不同强风化厚度对应的临界坡率，如图6所示。

由图6可以看出，临界坡率范围不小于1：1，不大于1：0.5，介于此区间；强风化岩层厚度占比超过1/2时，强风化岩层一定会发生破坏。

为了判断特定边坡强风化岩是否破坏，建立破坏分界线，即图6中黑线，并推导一般性公式，m为强风化岩厚度占比，n为坡率，得到临界坡率（界线）为

n=-3.86m+1.85 。  （2）

实际工程中，当强风化岩厚度占比超过1/2或坡率大于1：0.5时，强风化岩一定会发生破坏，需进行支护；当强风化岩厚度占比小于1/2且施工坡率介于1：1和1：0.5时，可根据开挖深度及强风化岩厚度占比确定临界坡率，应用式（2）进行判断：如果（m，n）点落在了分界线下方，强风化岩不破坏，边坡呈圆弧-平面滑动模式，下部岩体不需支护；如果落在分界线上方，则强风化岩可能会破坏，需要进行支护。文中只探讨强风化岩不发生破坏的情况，强风化岩破坏时的边坡另文研究。

3 强风化岩不破坏的土岩边坡破坏模式

3.1 圆弧平面滑动解析解

土与强风化岩双元边坡小于临界坡率时，破坏模式为圆弧-平面滑动破坏模式，下卧岩层不发生破坏。将滑动面以上坡体看作刚体，以此作为脱离体，分析整个滑动面上的抗滑力及下滑力，计算安全系数。

对坡体建立竖直条分模型[11]，如图7所示，其中，s指边坡滑移面；h为边坡高度；h2为中风化岩石的高度；r为圆弧滑动滑移面的圆心；β为坡角。竖直条分模型如图8所示，其中，dx为竖直土条的厚度；z1（x）为坡面的数学表达式；z2（x）为滑移面的数学表达式；θ为滑移面与水平方向的夹角。

x1为土层与中风化岩石交界面左处的x值；x2为坡顶处的x值；x3为土层与中风化岩石交界面右处的x值；x4为滑移面坡顶开裂点处的x值。x1，x2，x3，x4，z1（x），z2（x）的值为

{（x_1=h_2/tanβ （，&x_2=h/tanβ）（，&x_3=a+√（r^2-（b-h_2 ）^2 ））（，&x_4=a+√（r^2-〖（b-h）〗^2 ））@z_1 （x）=xtanβ，z_2 （x）=b-√（r^2-〖（x-a）〗^2 ））}。    （3）

由于x2和x3大小不同時，积分区间及土条重力dw不同，所以分2种情况求边坡安全系数解析解。

当x2

土条重力可表示为

dw={（γ_1 （z_1 （x）-h_2）dx（，&x_1≤x）

其他参数为

{σ=dwcosθ/dx （，&sinθ=（x-a）/r）（，&cosθ=√（r^2-〖（x-a）〗^2 ）/r）（，&ds=rdx/√（r^2-〖（x-a）〗^2 ））}。     （5）

为简化公式，便于程序计算，设定以下2个函数：

f（x）=[r^2-〖（x-a）〗^2 ]^（1/2） ，

g（x）=1/2 （x-a） （r^2-（x-a）^2 ）^（1/2）+r^2/2 arcsin （x-a）/r 。

土体的下滑力T1由各土条重度切向分量dT'构成，dT'为dT的相互作用力，dT'=dwsinθ。

（T_1=∫_（x_3）^（x_4）?dwsinθ=∫_（x_3）^（x_4）?〖γ_1 （h-b+√（r^2-〖（x-a）〗^2 ））（x-a）/r dx〗=@        （γ_1 （h-b））/r [1/2（x_4^2-x_3^2）-a（x_4-x_3）]   -γ_1/3r [f（x_4）-f（x_3）]。）   （6）

土体的抗滑力T2由滑动面处土体的剪应力及土岩交界面处的剪应力构成。

（T_2=∫_（x_3）^（x_4）?〖c_1 ds〗+∫_（x_3）^（x_4）?〖σtan?_1 dx〗=@∫_（x_3）^（x_4）?（c_1 r）/√（r^2-〖（x-a）〗^2 ） dx+∫_0^（x_2）?〖σtan?_1 dx〗   +∫_（x_2）^x3?〖σtan?_1 dx〗+∫_（x_3）^（x_4）?〖σtan?_1 dx〗=@c_1 r（arcsin （x_4-a）/r-arcsin （x_3-a）/r）  +tan?_1 {（γ_1 tanβ）/3r[f（x_1）-f（x_2）]+@  γ_1/r（atanβ-h_2）[g（x_2）-g（x_1）]  +γ_1/r（h-h_2）[g（x_3）-g（x_2）]+@  （γ_1 （h-b））/r[g（x_4）-g（x_3）]  +γ_1/r[（r^2 x_4-1/3（x_4 〖-a）〗^3）  -（r^2 x_3-1/3（x_3 〖-a）〗^3）]}。） （7）

当x2>x3时，参数示意如图10所示。

土条重力可表示为

dw={（γ_1 （z_1 （x）-h_2）dx       （，&x_1≤x）

土体的下滑力T1由各土条重度切向分量dT'构成，dT'为dT的相互作用力，dT'=dwsinθ。

（T_1=∫_（x_3）^（x_4）?dwsinθ=@       ∫_（x_3）^（x_2）?〖γ_1 （xtanβ-b+√（r^2-〖（x-a）〗^2 ））（x-a）/r dx〗+  ∫_（x_2）^（x_4）?〖γ_1 （h-b+√（r^2-〖（x-a）〗^2 ））（x-a）/r dx〗=@       （γ_1 tanβ）/r [1/3（x_2^3-x_3^3）-a/2（x_2^2-x_3^2）]+  （γ_1 b）/r [1/2（x_2^2-x_3^2）-a（x_2-x_3）]+@       （γ_1 （h-b））/r [1/2（x_4^2-x_3^2）-a（x_4-x_3）]   -γ_1/3r [f（x_4）-f（x_3）]。）   （9）

土体的抗滑力T2由滑动面处土体的剪应力及土岩交界面处的剪应力构成。

（T_2=∫_（x_3）^（x_4）?〖c_1 ds〗+∫_（x_3）^（x_4）?〖σtan?_1 dx〗=@       ∫_（x_3）^（x_4）?（c_1 r）/√（r^2-〖（x-a）〗^2 ） dx+∫_0^（x_3）?〖σtan?_1 dx〗   +∫_（x_3）^（x_2）?〖σtan?_1 dx〗+∫_（x_2）^（x_4）?〖σtan?_1 dx〗=@       c_1 r（arcsin （x_4-a）/r-arcsin （x_3-a）/r）  +tan?_1 {（γ_1 tanβ）/3r（f（x_1）-f（x_3））+@       γ_1/r（atanβ-h_2）[g（x_3）-g（x_1）]  +γ_1/r（atanβ-b）[g（x_2）-g（x_3）]+@       γ_1/r[r^2 （x_4-x_3）-1/3[（x_4 〖-a）〗^3-（x_3 〖-a）〗^3]]+  （γ_1 （h-b））/r[g（x_4）-g（x_2）]}。）    （10）

安全系数F_s表示为

F_s=M_2/M_1 =（rT_2）/（rT_1 ）=T_2/T_1 。  （11）

3.2 算例验证

为验证公式的正确性，将使用文中公式得到的安全系数与有限元法进行对照。选取文献[3]的济南某基坑工程案例剖面，基坑边坡由土与强风化岩构成。Plaxis3D模拟的滑移面如图11所示。滑坡体全部位于土层中，强风化岩没有发生破坏。滑出点在坡面，使用公式（11）计算安全系数。

具体参数为：

滑移面圆心，b=29.802 m，半径r=34.83 m，边坡高h=10 m，倾斜角β=45°。

土的黏聚力c_1=10 kN/m^2，内摩擦角?_1=20°，重度γ_1=18 kN/m^2。

强风化岩的黏聚力c_2=60 kN/m^2，内摩擦角?_2=45°，重度γ_2=22.5 kN/m^2。

用Matlab计算公式（11）得出安全系数为1.4231，用Plaxis3D模拟出的安全系数为1.45，差距不大，证明稳定性解析解的结果是正确的。由于瑞典条分法忽略了条间力的平衡，所以在竖直条分模型中会放大下滑力矩条只满足力矩的平衡[30]，不满足力的平衡，导致解析解得到的安全系数结果偏小，是较为安全的结果。

3.3 边坡破坏滑移曲线的确定

由于解析解的应用需要指定圆弧的圆心和半径，应用滑移线场法[31]，得出边坡的滑移曲线[32?35]。针对济南大众传媒大厦基坑工程案例，某设计单元剖面地层，土加强风化岩基坑边坡土层参数按表3选取，岩层参数按表1选取。边坡开挖深度为10 m，坡率为1：1。由Plaxis3d有限元软件计算出边坡临界状态的应力场，编制专用程序求解临界滑移线，得到的滑移线，如图12所示。

使用3.1節推出的边坡稳定解析解公式（11）计算边坡临界滑移线的安全系数，各滑移线安全系数自上而下分别为1.635、1.593、1.521、1.432。安全系数最小为1.432，对应的滑移线即为临界滑移线。使用有限元软件计算得到的安全系数为1.49，验证了文中方法的正确性。

为得到边坡的滑移线解析解，使用Matlab进行公式拟合，以坡脚为坐标原点，得到的临界滑移线表达式如下。对公式进行误差分析，方差为0.23，不超过0.5，拟合效果较好。

{（z_圆弧=√（148-（x-8.3）^2 ）+13.2，5≤z≤10 ；@z_直线=5"" （（" "&）&&&             ，）0≤z≤5。）┤

4 强风化岩未破坏的边坡设计方法

选取济南市立四院某设计单元剖面地层，边坡由土+全风化岩+强风化岩构成，土层厚度为2.9 m，全风化岩层为3.2 m，强风化岩厚度为6 m，边坡高度为12 m，坡角为60°。土层参数如表4所示，强风化岩参数如表5所示。当边坡不进行支护时，使用Plaxis3d模拟得到的边坡安全系数为0.835，开挖时边坡会倒塌，因此需对边坡进行支护，使用文中方法进行支护区域判断。先将强风化岩厚度占比0.5代入公式（2），再将得到的（m，n）与图6对应，位于分界线下方，强风化岩不必支护。使用软件进行土钉墙支护设计，为加强交界面抗滑能力，第三道土钉深入强风化岩。土钉布置情况如表6所示，支护剖面如图13所示。

使用Ｐlaxis3D进行模拟，模型设计参照图2所示，计算边坡的应力场。由图14可知，强风化岩层没有发生破坏，整体仍为圆弧平面滑动，验证了第3节的结论。安全系数为1.548，大于规范[5]要求的一级边坡工程安全系数1.35，满足安全性要求。

将得到的边坡应力场代入Matlab程序，得到边坡的潜在滑移线公式为

{（z_圆弧=√（234.09-〖（x-2.05）〗^2 ）+18.37，6≤z≤12；@z_直线=6"" （（  " "&&）&&&）              ，0≤z≤6。）┤

潜在滑移线公式确定了边坡的潜在破坏区域，经验证，在支护设计时，土钉已刺穿潜在滑移线，达到了支护效果。

5 结  论

文中基于济南地区土与强风化岩双元边坡地质条件，采用数值模拟的方法获得强风化岩破坏体出现的临界坡率，并针对强风化岩不发生破坏的边坡，根据滑移线场法求出潜在滑移线的位置，推出土与强风化岩边坡破坏模式曲线方程，推导出边坡安全系数解析解。得出结论如下：

1）土与强风化岩双元边坡破坏存在岩体破坏和不破坏2种模式，可通过临界坡率划分。临界坡率与边坡高度、土岩厚度及其比例相关。

2）强风化岩厚度超过边坡高度1/2或坡率大于1：0.5时，强风化岩一定破坏，破坏范围和坡率与临界坡率的差值有关，差值越大，破坏范围越大。

3）基于瑞典条分法的圆弧-平面安全系数解析解，其得出的安全系数小于有限元法安全系数，应用解析解工程决策优于有限元法。

4）对于强风化岩不发生破坏的土岩边坡，利用常用软件完成强风化岩上部地层支护方案设计，所得安全系数满足规范要求，可保证边坡安全。

参考文献

［1］  杨丽芝， 曲万龙， 刘春华， 等. 济南城市工程地质条件分区及轨道交通建设适宜性研究[J]. 水资源与水工程学报， 2012， 23（6）： 120-123.

Yang L Z， Qu W L， Liu C H， et al. Analysis of suitability about the division of engineering geological condition and rail transit construction in Jinan urbon area[J]. Journal of Water Resources and Water Engineering， 2012， 23（6）： 120-123.（in Chinese）

［2］  山东省住房和城乡建设厅， 山东省市场监督管理局. 济南市区岩土工程勘察地层层序划分标准： DB37/T 5131—2019[S] .济南：山东大学出版社，2019.

Housing and Urban-Rural Development Department of Shandong Province， Shandong Administration for Market Regulation. Division code for stratigraphic sequence of engineering investigation in Jinan City： DB37/T 5131—2019[S]. Jinan： Shandong University Press， 2019. （in Chinese）

［3］  王兴政. 济南市典型土岩双元基坑破坏模式及其支护结构选型研究[D]. 济南： 山东大学， 2017.

Wang X Z. Study on failure mode of typical soil-rock foundation pit in Jinan and the support structure selection[D]. Jinan： Shandong University， 2017. （in Chinese）

［4］  中华人民共和国住房和城乡建设部. 建筑基坑支護技术规程：JGJ 120-2012[S]. 北京： 中国建筑工业出版社， 2012.

Ministry of Housing and Urban-Rural Development of the Peoples Republic of China. Technical specification for retaining and protection of building foundation excavation： JGJ 120-2012[S]. Beijing： China Architecture Publishing & Media Co.， Ltd.， 2012. （in Chinese）

［5］  中华人民共和国住房和城乡建设部， 中华人民共和国国家质量监督检验检疫总局. 建筑边坡工程技术规范： GB 503302013[S]. 北京： 中国建筑工业出版社， 2013.

Ministry of Housing and Urban-Rural Development of the Peoples Republic of China， General Administration of Quality Supervision， Inspection and Quarantine of the Peoples Republic of China. Technical code for building slope engineering： GB 503302013[S]. Beijing： China Architecture Publishing & Media Co.， Ltd.， 2013. （in Chinese）

［6］  刘红军， 王亚军， 姜德鸿， 等. 土岩组合双排吊脚桩桩锚支护基坑变形数值分析[J]. 岩石力学与工程学报， 2011， 30（S2）： 4099-4103.

Liu H J， Wang Y J， Jiang D H， et al. Numerical analysis of deep foundation pit displacement with double-row end-suspended piles in strata of soil-rock dualistic structure[J]. Chinese Journal of Rock Mechanics and Engineering， 2011， 30（S2）： 4099-4103.（in Chinese）

［7］  刘红军， 李东， 孙涛， 等. 二元结构岩土基坑“吊脚桩”支护设计数值分析[J]. 土木建筑与环境工程， 2009， 31（5）： 43-48.

Liu H J， Li D， Sun T， et al. Numerical analysis on design of dualistic foundation pit with ‘end-suspended pile[J]. Journal of Civil，Architectural & Environmental Engineering， 2009， 31（5）： 43-48.（in Chinese）

［8］  Bishop A W. The use of the slip circle in the stability analysis of slopes[J]. Géotechnique， 1955， 5（1）： 7-17.

［9］  Sarma S K. Stability analysis of embankments and slopes[J]. Journal of the Geotechnical Engineering Division， 1979， 105（12）： 1511-1524.

［10］  Morgenstern N R， Price V E. The analysis of the stability of general slip surfaces[J]. Géotechnique， 1965， 15（1）： 79-93.

［11］  卢玉林， 薄景山， 陈晓冉， 等. 瑞典圆弧法积分模型的边坡稳定性解析计算[J]. 应用力学学报， 2017， 34（2）： 257-263，402.

Lu Y L， Bo J S， Chen X R， et al. Analytical formulation of slope stability based on Sweden arc integral model[J]. Chinese Journal of Applied Mechanics， 2017， 34（2）： 257-263，402.（in Chinese）

［12］  Janbu N. Application of composite slip surface for stability analysis[J]. Eurpoean Conference on  Stability of Earth Slopes， 1954（3）： 43-49.

［13］  張磊. 简化瑞典条分法在土坡稳定分析中的应用[D]. 北京： 中国地质大学， 2007.

Zhang L. The apply of simplified fellenius method in soil slope stability analysis[D]. Beijing： China University of Geosciences， 2007. （in Chinese）

［14］  戴自航， 沈蒲生. 土坡稳定分析简化Bishop法的数值解[J]. 岩土力学， 2002， 23（6）： 760-764.

Dai Z H， Shen P S. Numerical solution of simplified Bishop method for stability analysis of soil slopes[J]. Rock and Soil Mechanics， 2002， 23（6）： 760-764.（in Chinese）

［15］  李凯， 陈国荣. 基于滑移线场理论的边坡稳定性有限元分析[J]. 河海大学学报（自然科学版）， 2010， 38（2）： 191-195.

Li K， Chen G R. Finite element analysis of slope stability based on theory of slip line field[J]. Journal of Hohai University （Natural Sciences）， 2010， 38（2）： 191-195.（in Chinese）

［16］  龚文惠， 陈训龙， 邱金伟， 等. 基于滑移线场理论的地震作用下土质边坡稳定性分析[J]. 岩土力学， 2017， 38（6）：1733-1738.

Gong W H， Chen X L， Qiu J W， et al. Seismic stability analysis of soil slope using theory of slip line field[J]. Rock and Soil Mechanics， 2017， 38（6）：1733-1738.（in Chinese）

［17］  李剑， 陈善雄， 余飞. 基于最大剪应变增量的边坡潜在滑动面搜索[J]. 岩土力学， 2013， 34（S1）： 371-378.

Li J， Chen S X， Yu F. A method for searching potential failure surface of slope based on maximum shear strain increment[J]. Rock and Soil Mechanics， 2013， 34（S1）： 371-378.（in Chinese）

［18］  Spencer E. A method of analysis of the stability of embankments assuming parallel inter-slice forces[J]. Géotechnique， 1968， 18（3）： 384-386.

［19］  Marsal R J. Large scale testing of rockfill materials[J]. Journal of the Soil Mechanics and Foundations Division， 1967， 93（2）： 27-43.

［20］  方宏伟， 李长洪， 李波. 均质边坡稳定性极限曲线法[J]. 岩土力学， 2014， 35（S1）： 156-164.

Fang H W， Li C H， Li B. Limit curve method of homogeneous slope stability[J]. Rock and Soil Mechanics， 2014， 35（S1）： 156-164.（in Chinese）

［21］  Zheng Y R，Liu Y X.Development of plastic potential theory and its application in constitutive models of geomaterials[C]//9th International Conference on Computer Method and Advance in Geomechanics. Rotterdam： Balkema Publisher， 1997：941-946.

［22］  Chen W F.Limit analysis and soil plasticity[M].Berlin：Elsevier Scientific Press，1975.

［23］  Kabilamany K， Ishihara K. Stress dilatancy and hardening laws for rigid granular model of sand[J]. Soil Dynamics and Earthquake Engineering， 1990， 9（2）： 66-77.

［24］  张国祥， 刘宝琛. 潜在滑移线法分析边坡滑动面及稳定性[J]. 土木工程学报， 2002， 35（6）： 82-85.

Zhang G X， Liu B C. Analysis of slope slip surface and stability by the potential slip surface theory[J]. China Civil Engineering Journal， 2002， 35（6）： 82-85.（in Chinese）

［25］  王昌业. 基于滑移线法的边坡临界滑动面搜索方法研究[D]. 西安： 长安大学， 2013.

Wang C Y. The research on the method about tracking the critical sliding surface of the slope with the slip line theory[D]. Xi'an： Changan University， 2013. （in Chinese）

［26］  张国祥， 刘新华， 魏伟. 二维边坡滑动面及稳定性弹塑性有限元分析[J]. 铁道学报， 2003， 25（2）： 79-83.

Zhang G X， Liu X H， Wei W. Analysis of elastic-plastic finite element for two dimension slope slip surface and stability[J]. Journal of the China Railway Society， 2003， 25（2）： 79-83.（in Chinese）

［27］  李连祥， 刘嘉典， 李克金， 等. 济南典型地层HSS参数选取及适用性研究[J]. 岩土力学， 2019， 40（10）： 4021-4029.

Li L X， Liu J D， Li K J， et al. Study of parameters selection and applicability of HSS model in typical stratum of Jinan[J]. Rock and Soil Mechanics， 2019， 40（10）： 4021-4029.（in Chinese）

［28］  尹驥. 小应变硬化土模型在上海地区深基坑工程中的应用[J]. 岩土工程学报， 2010， 32（S1）： 166-172.

Yin J. Application of hardening soil model with small strain stiffness in deep foundation pits in Shanghai[J]. Chinese Journal of Geotechnical Engineering， 2010， 32（S1）： 166-172.（in Chinese）

［29］  姜晓婷， 路平， 郑刚， 等. 天津软土地区盾构掘进对上方建筑物影响分析[J]. 岩土力学， 2014， 35（S2）： 535-542.

Jiang X T， Lu P， Zheng G， et al. Influences on surface structure induced by shield tunneling in Tianjin soft ground area[J]. Rock and Soil Mechanics， 2014， 35（S2）： 535-542.（in Chinese）

［30］  卢玉林， 薄景山， 陈晓冉. 瑞典圆弧法水平条分模型的误差分析[J]. 地震工程学报， 2017， 39（3）： 496-501.

Lu Y L， Bo J S， Chen X R. Error analysis of a horizontal slice model using the Swedish arc method[J]. China Earthquake Engineering Journal， 2017， 39（3）： 496-501.（in Chinese）

［31］  Davis E H. Theories of plasticity and the failure of soil masses[M]. In：Lee I K ed.Soil Mechanics.London：Utterworth，1968.341-380.

［32］  朱以文， 吴春秋， 蔡元奇. 基于滑移线场理论的边坡滑裂面确定方法[J]. 岩石力学与工程学报， 2005， 24（15）： 2609-2616.

Zhu Y W， Wu C Q， Cai Y Q. Determination of slip surface in slope based on theory of slip line field[J]. Chinese Journal of Rock Mechanics and Engineering， 2005， 24（15）： 2609-2616.（in Chinese）

［33］  高政国， 刘思海， 黄新. 基于强度折减法的边坡滑动破坏分析[J]. 地下空间与工程学报， 2013， 9（S1）： 1531-1535.

Gao Z G， Liu S H， Huang X. Slope slide-failure analysis based on strength reduction method[J]. Chinese Journal of Underground Space and Engineering， 2013， 9（S1）： 1531-1535.（in Chinese）

［34］  Griffiths D V， Lane P A. Slope stability analysis by finite elements[J]. Géotechnique， 1999， 49（3）： 387-403.

［35］  趙尚毅， 郑颖人， 时卫民， 等. 用有限元强度折减法求边坡稳定安全系数[J]. 岩土工程学报， 2002， 24（3）： 343-346.

Zhao S Y， Zheng Y R， Shi W M， et al. Analysis on safety factor of slope by strength reduction FEM[J]. Chinese Journal of Geotechnical Engineering， 2002， 24（3）： 343-346.（in Chinese）

（编辑  陈移峰）