教育数学、数学建模与桥牌的数学定律
蒋启芬, 朱佳俊, 张跃辉,2
(1.上海交通大学 数学科学学院,上海 200240; 2.上海交通大学 教育学院,上海 200240)
0 引 言
张景中院士倡导的教育数学逐渐深入人心,不但因为教育数学“把数学变简单”的理念极大地提升了中小学数学教与学的水平和效率,而且因为教育数学三原理为所有数学课程的教学提供了一套脚踏实地、循序渐进、行之有效的操作程序.
张景中院士提出,教育数学的根本目的,通俗的说就是使学生在“更少的时间内学得更多更好,更现代化,更津津有味.”[1]张景中院士提出实现该目标的教育数学三原理为,第一条原理:在学生头脑里找概念;第二条原理:从概念里产生方法;第三条原理:方法要形成模式.
数学教育、实际上任何教育都要遵循教育的基本规律.什么是教育的基本规律?赵沁平院士在其论文集《让教育规律成为常识》[2]中,引用孔子《论语》的“不怨天,不尤人,下学而上达”以及朱熹的批注“反己自修,循序渐进耳”,来说明循序渐进是教育第一规律,因为“教育即生长”,成语“揠苗助长”也从反面说明教育第一规律是人类几千年智慧的结晶,不容违背;而“概念”与“模式”正是数学三要素中最重要的“严格性”与“抽象性”的体现:只有找到严格的概念,才可能产生有效的方法,最终形成放之四海而皆准的抽象模式.沈文选在《走进教育数学》[3]中将教育数学命名为第四座“数学宫殿”,指出了其与数学教育的本质区别:数学教育的主要研究对象是“数学教什么”与“怎么教数学”两大主题,而教育数学的主要研究对象则是“数学究竟是什么”这一根本性问题.张景中院士“为了教育,改造数学”可以说扣紧了“教育数学”的脉搏,对从根本上解决我国初等教育重解题思路、轻提问质疑、弱抽象思维、略概念提炼等痼疾开出了一剂对症下药的良方.所以,教育数学由“找概念”渐进为“生方法”最终升华为“成模式”的理念,不但抓住了教育数学的深刻内涵,而且把握住了数学教育的本质规律.因此,本文通讯作者在全国教育数学2022年学术年会报告中将教育数学三原理整理为,第一原理:培养学生找概念;第二原理:钻研概念生方法;第三原理:精炼方法成模式.
本文以教育数学的思想理论研究桥牌理论的最新研究成果《桥牌的数学定律》[4],深入分析教育数学的基本理论对建立桥牌数学模型的指导作用,完整展现根据教育数学原理在数学课程和数学建模教学中产生新方法、新模式的全过程.
按照教育数学“让数学变简单”的根本原理,《桥牌的数学定律》抓住桥牌“长强互伴”,即“单一花色的长度与强度相互依存”这个桥牌运动的本质规律,首次提出了“长度与强度同分布”这一熟视无睹但极为可靠的简单桥牌假设,从而推导出迄今为止最为简洁的桥牌数学模型即“桥牌分布定理”[2],被加拿大工程院院士杨春生教授誉为“桥牌理论的杰作”;该书出版一个月作者即被北美华人桥牌协会邀请作面向全世界的桥牌理论报告“桥牌的数学定律”;连续三年高居世界桥牌女子第一人的我国著名国手王文霏特级大师在为该书的序中称“书中的某些叫牌理论惊艳到了我”.
桥牌分为叫牌与打牌两个阶段.叫牌阶段四家的牌都是暗的,因此关键在于估算其余三家的牌;而打牌阶段明手要摊牌,因此首攻之后的关键在于更为准确地计算其余两家的几何结构与代数结构.《桥牌的数学定律》是目前研究桥牌数学模型的第一本专著,但由于该书的主要读者大多是非数学背景,因此出版物中呈现给广大爱好者的数学模型非常简单,并且略去了建模的全部过程,当然就使读者非常遗憾地失去了感悟教育数学理念和强大威力的大好时机.
本文的目的就是利用两种不同方法即古典概率模型和教育数学原理,全面展现建立桥牌数学模型的完整过程,从而使广大读者和桥牌爱好者切实感受到教育数学三原理对数学建模在普及数学方面的巨大作用,阐述教育数学三原理对数学课程教学改革的指导意义.
1 教育数学与桥牌的数学定律
本节1.1小节利用古典概率直接建立桥牌的数学模型;1.2小节利用教育数学三原理,先假设“长强互伴”,再建立桥牌的数学模型;1.3小节比较分析两种方法的优缺点.
1.1 桥牌的数学模型
(P1)p是“保序的”,即若C1,C2是B中同花色牌张,且C1 (P2)p是“无偏的”,即若C1,C2是B中异花色牌张,且C1与C2牌值相同,则p(C1)=p(C2). 该映射p称为“赋值函数”,对B中任意元素x,p(x)称为x的赋值,这就是通常的大牌点.小于10的牌取得1墩的概率是非常低的,将其大牌点一律定义为0不会产生显著误差,却能使桥牌的数学模型大为简化,符合数学建模的根本理念.所以本文剩余部分的讨论将约定赋值函数p还满足条件p(A)>p(K)>p(Q)>p(J)>p(10)=0,实际上几乎所有简单高效的大牌点系统都采用该假设. 所以 按照教育数学第一原理“培养学生找概念”,生活中的常识往往是“找概念”的好地方,那么,哪里是反映桥牌本质规律的常识呢? 桥牌选手和爱好者普遍接受的桥牌常识是所谓“长强相依”,即套越长,点越多;点越多,套越长.“长强相依”的数学化就是“每门花色的大牌点数与长度成正比”.《桥牌的数学定律》正是根据“长强相依”这个桥牌常识循序渐进地得出了如下的基本假设: 通俗分布定律随机牌组的大牌点与牌型同分布. 《桥牌的数学定律》中“随机牌组”“牌型分布”“赋值函数”等数学概念,正是深入研究“通俗分布定律”这一桥牌常识的产物,是遵循教育数学理念、践行教育数学三原理的成果. 由通俗分布定律即可建立下述桥牌运动的数学模型. 牌张分布定理设Y是一个随机牌组,l,p,L,P分别是Y的牌型分布、大牌分布、长度与赋值总数.设E(l)与E(p)分别表示l与p的数学期望.则 在牌张分布定理中取L=13,赋值函数为沃克计点法,即可得到下面适合实战的快速计算定理. 桥牌分布定理设Y是一个随机牌组,l,p,L,P分别是Y的牌型分布、大牌分布、长度与大牌点总数.设E(l)与E(p)分别表示l与p的数学期望.则 仅举一例阐释桥牌分布定理的作用. 例1(i) 任取1张牌是A的概率为1÷13≈0.08,是花牌的概率为4÷13≈0.31. (iii) 牌张分布定理可以精确解释经验法则“空位理论(vacancy theory)”[5].假定防守方未参与叫牌,您是庄家.首攻3,上家垫了一张,您立即推算出6-0分布,现在需要判断哪个防家持有◆Q? 您知道首攻人与上家各有7张和12张暗牌.在没有其它信息之前,牌张分布定理告诉我们,上家与首攻人持有◆Q的概率之比是12∶7. “牌张分布定理”是精确的数学定理,不仅适用于桥牌,也适用于其它所有的纸牌游戏. 由桥牌常识找出的数学概念导致大量桥牌新方法的产生,是教育数学第二原理“钻研概念生方法”的有力佐证.比如传统的弱二高花等阻击叫是长期经验的积累,并无太多数学理论支撑,然而由牌张分布定理可以证明,弱牌双套5-5以上时的2~3阶阻击开叫具有更大威力,此即“双套赢墩定理”(见下文),上海交通大学桥牌队即是以这套理论为指导方针,勇夺2021年上海市教职工第九届桥牌运动会个人第一和团体铜牌. 继续研究由牌张分布定理产生的诸多新方法,《桥牌的数学定律》在最后一章“几何结构与双套定理”中证明了下面的定理. 双套赢墩定理记联手最长双套的较长长度分别为L1,L2,B为双套所缺A,K总数,F为其余短套快速赢张总数.设联手双套至少9-8配合,则有概率不等式 p(T≥L1+L2-B+F)>0.6. 双套赢墩定理是桥牌的一种普适模式(对联手双套配合或双套互补均有效),其产生过程是教育数学第三原理“精炼方法成模式”行之有效的最好例证.模式即普适的理论,必定产生于成熟的方法,这个结论既是教育数学三原理的精髓,也是我国传统教育理念“熟能生巧”的升华,不但适合中小学的教与学,也完全适合高等教育的教与学乃至所有科学研究. 本文1.1小节直接从数学专业的角度即古典概率建立桥牌的数学模型,优点是严格性与概括性高,缺点也十分显著,那就是除了数学工作者外,绝大多数读者都一头雾水不知所云,无助于桥牌普及. 与1.1小节的处理方法相反,本文1.2小节完全遵照教育数学三原理建立桥牌的数学模型,严格性与概括性等标准与1.1小节完全相同,然而由于出发点是从常识里“找概念”,因此所有读者不但能够完全明白每个数学概念的含义和背景,而且能够深刻理解桥牌的数学模型的内涵和应用,从而可以在实战中熟练应用基于数学模型导出的多个桥牌的数学定律. 两个完全等价的数学模型为什么产生的学习效果却大相径庭?根本原因在于著名数学教育家张奠宙提出的数学形态理论.张奠宙[6]指出,数学知识具有三种形态,“原始形态、学术形态和教育形态”,前二者显然都不适合中小学乃至大学课堂,而“教育数学是具有教育形态的数学”,是适合课堂教学的数学. 知识形态理论适合于所有学科.现有的桥牌理论研究大多处于原始形态,对桥牌普及的推动作用不大;《桥牌的数学定律》则兼具学术形态和教育形态,既适合研究者求同存异,也适合专业牌手学习理论,更适合于爱好者普及推广.以双套赢墩定理为例,1.1小节与1.2小节各自的数学模型是等价的,当然都能够导出双套赢墩定理,所有读者都能够完全理解并熟练运用1.2小节的双套赢墩定理,因为这是一个处于“教育形态”适合所有学生和读者的理论结果;但绝大多数读者很难接受源自1.1小节古典概率模型的双套赢墩定理,因为这个结果完全处于“学术形态”而不适合课堂教学或普及推广,此情形与被《桥牌的数学定律》称为桥牌第一定律的“总墩数定律”类似.在双套赢墩定理之前,上世纪六十年代被发现的总墩数定律是桥牌理论界唯一可以应用的近似公式,但由于其产生过程完全神秘,可靠性仅有1996年美国计算机学家、桥牌选手Ginsberg[7]的样本量不大的计算机模拟数据,因此遭到了包括世界冠军Lawrence等人的强烈反对[8],直到《桥牌的数学定律》将其按照教育数学的“简单化”原理,分解为部分定约与非部分定约之后,方才第一次证明了总墩数定律对部分定约显著可靠. 双套赢墩定理是世界上首次由桥牌的数学模型推导出来的严格数学定理,其可靠性不言而喻,而其产生的过程则与总墩数定律完全不同,是严格遵照教育数学原理发现的.更精确地说,双套赢墩定理的产生完全符合教育数学所倡导的循序渐进的科学过程:第一步,“找概念”源自对桥牌常识“长强相依”的凝练而找到的“长度向量”与“强度向量”等数学概念,由此即可建立迄今为止最简单最有效的桥牌数学模型;第二步,“生方法”源自对数学概念“长度向量”与“强度向量”等的深度研究,结果是产生了桥牌运动最根本最重要的数学理论即牌张分布定理;第三步,“成模式”则是对牌张分布定理进行有的放矢的广泛应用,分别产生或证明了适合部分定约的总墩数定律、适合成局定约的赢张定律、适合有将满贯定约的短控定律,以及世界上首次发现的双套赢墩定理. 教育数学是中国学者自己创造的卓越教育理论,是我国对世界教育理论的巨大贡献.该理论自张景中院士于上世纪七十年代创建以来,取得了巨大成效.与孟子“得天下英才而教育之”的君子三乐有所不同,张景中院士运用教育数学原理将入学成绩较差的学生教育为中考数学100%优秀,而且实验班的所有学生在七年级下就能掌握正弦定理与正弦和角公式,八年级上就能掌握余弦定理,在义务教育阶段掌握三角形的作图推理与计算[1-3].这是世界教育史上从未有过的奇迹,彰显了我国教育理论数千年的深厚积淀、无穷魅力和强大生命力. 《桥牌的数学定律》运用教育数学三原理研究具有百年历史、被誉为“智运之王”的桥牌运动,鞭辟入里地建立了桥牌的简明数学模型,深入浅出地揭示了桥牌的本质数学定律,将被认为是最难的智力运动、“聪明人的游戏”的桥牌运动变为通俗易懂、入门友好、老少咸宜的普通智力游戏.教育数学使数学更简单这个朴素思想的巨大威力在此书中体现得淋漓尽致. 由此及彼、由表及里,数学教师乃至所有教育工作者一旦深入理解、熟练掌握并自觉应用教育数学的基本理论,其教学理念必然革故鼎新,其教学水平必然脱胎换骨,其教学效果必然日新月异,其教育对象也必然获益匪浅、进步神速.总之,教育数学的基本理论特别是教育数学三原理对我国的教育改革具有巨大的推动作用,对所有教育工作者乃至科学工作者极有裨益,值得认真学习、深入研究和大力推广. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.
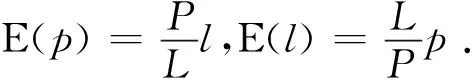
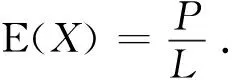

1.2 教育数学与桥牌的数学模型
1.3 比较分析
2 结 论

