基于切向量的两类曲线积分的关系
吴淑君, 于 娟
(中国石油大学(华东) 理学院,山东 青岛 266580)
0 引 言
第二类曲线积分是多元函数积分学中的重要内容[1-2],很多文献已经从理论、教法等方面讨论了该积分的计算[3-5].其中,两类曲线积分之间的关系是一个重要的公式:
(1)
其中cosα,cosβ是“有向曲线弧的切向量”的方向余弦.
在文献[1]中,“有向曲线弧的切向量”定义为 “指向与有向曲线弧的方向一致的切向量”.这个定义是在文献[1]中8.6这一节,利用向量值函数的导数结合几何直观给出的.文献[6]曾指出文献[1]中的缺陷,并加以改进(1).文献[7]以弧长作为参数,用极限的方法严格证明了在文献[2]中提出的 “有向曲线弧的切向量”的表达式,并推导出(1).
在教学中注意到,如果按照文献[1]的授课顺序,学生会对突然插入的向量值函数感觉很突兀,不容易理解向量值函数的导数,也不能全面深刻地掌握切向量和曲线方向以及参数变化之间关系.受文献[7]的启发,不再引入向量值函数,而是用一般的参数,借助极限的基本方法求出切向量.具体来说,利用切线是割线的极限位置这个学生熟悉的知识点,证明切向量的表达式,该过程可以直观地展示出切向量和曲线方向以及参数变化的关系.
1 提出问题
假设平面曲线L的两个端点分别记为A和B,曲线的参数方程是
端点A和B对应的参数分别是t1和t2.M(x,y)是L上的一个点,对应参数为t.函数x(t),y(t)在以t1和t2为端点的区间上具有一阶连续导数,且(x′(t))2+(y′(t))2≠0.曲线的方向是从A到B.下面针对不同的情况,先用极限计算出M处的切向量,进而推出两类曲线积分之间的关系.
2 解决问题
根据两个端点参数的大小关系,分为两种情况讨论,即t1>t2和t1 为了求切向量,在下面的讨论中,将切向量的极限转化为平面上两点之间的距离问题,避免了向量值函数的极限和导数. 2.1.1 按照参数的增大的方向求切向量 图1 反向 进一步地,当T的方向角分别为α,β时,有 (2) 按照第二类曲线积分的计算公式,有 (3) 当t1>t2时,根据第一类曲线分的计算公式与(2), 所以 (4) 2.1.2 按照参数减小的方向求切向量 (5) 图2 同向 当t1>t2时,根据第一类曲线分的计算公式与(5), 由(3),得到 即公式(1)成立. 2.2.1 按照参数增大的方向求切向量 如图2所示,按照参数增大的方向,即曲线L的正向,在M点右侧且在曲线上任取一点N(x+Δx,y+Δy),对应的参数仍记为t+Δt,此时Δt>0.按照上述完全相同的讨论,可以得到切向量是T=(x′(t),y′(t)).注意,此时切向量T指向参数增大的方向,并且与曲线的正向一致.并且,切向量的方向余弦用(2)式来表示. 当t1 由(3),得到 即(1)式成立. 2.2.2 按照参数减小的方向求切向量 如图1所示,按照参数减小的方向,即曲线L的反向,M左侧且在L上的一点N(x+Δx,y+Δy),N对应的参数是t+Δt,此时Δt<0.可以求得切向量是T=(-x′(t),-y′(t)).注意,此时切向量T指向参数减小的方向,并且与曲线的反向一致.此时,切向量的方向余弦用(5)式来表示. 当t1 由(3),得到 即公式(4)成立. 解曲线L∶y=x2,x∶1→0.符合情况2.1,并且 (6) 如果按照2.1.1,有 (7) (8) 所以 也验证了(4)式成立. 如果按照2.1.2,有 (9) 利用(6)式、(8)式和(9)式,有 也验证了(1)式成立. 解曲线L∶y=x2,x∶0→1,符合情况2.2,并且 (10) 如果按照2.2.1,则(7)式成立,再联合(10)式,有 说明(1)式成立. 如果按照2.2.2,则(9)成立.联合(8)式和(10)式,有 验证了(4)式成立. 综上,利用极限严格证明了,无论给定的曲线方向如何,只要按照参数增大方向选取切向量,方向余弦都可以用(2)式来表示.反之,切向量的方向余弦都用(5)式来表示.进一步地,如果曲线的方向是根据参数的递减来确定的,即情况2.1,两类曲线积分之间的关系在不同的切向量的取法下相差一个负号;同理,如果曲线的方向是根据参数的递增来确定的,即情况2.2,两类曲线积分之间的关系在不同的切向量的取法下也相差一个负号.这说明了,讨论两类曲线积分之间的关系时,可以借助参数的变化来确定切向量,进而得到了两种关系式,即(1)和(4).但实际上,两种关系式的本质是一样的,所以很多教材直接统一为(1)式.在最后的两个例子里,也说明了虽然相差一个负号,但是对于具体的问题来说,只要给定了曲线的方向,两类曲线积分之间的关系是唯一确定的.本文展开为四种具体情况来讨论,并利用实例验证了结论,能帮助学生更好地理解切向量、参数、曲线方向之间的关系,准确把握第二类曲线积分的方向性和两类曲线积分之间的关系. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.2.1 当t1>t2时,曲线的正向和参数减少的方向一致



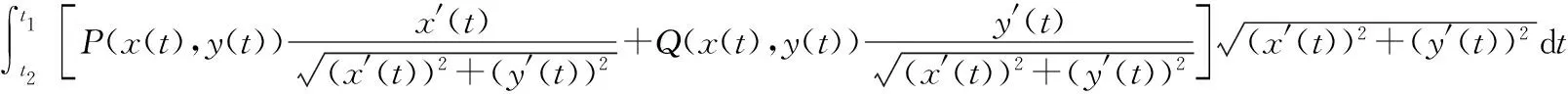

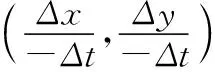



2.2 当t1


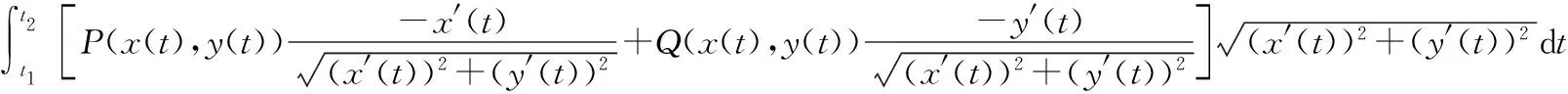

3 应 用

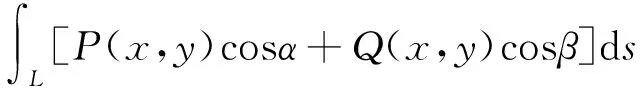


4 结 论

