基本概率赋值不确定性的广义度量及在证据组合中的应用
于 爽,王 欣,2†
(1.黑龙江大学自动化系,黑龙江哈尔滨 150080;2.黑龙江省信息融合估计与检测重点实验室,黑龙江哈尔滨 150080)
1 引言
由于噪声的干扰、传感器的老化、信号在信道传输过程中的衰减以及外界环境的复杂性等,使得传感器测量的信息具有强烈的不确定性,不确定性已成为信息的固有属性.D-S(dempster-shafer)证据理论在处理不确定信息和未知信息方面采用了乐观估计和悲观估计作为区间估计的上下界,而不是传统的点估计方法来处理数据,而通过贝叶斯概率转换,D-S证据理论又可以将区间估计转化为点估计,因此,D-S证据理论已成为处理不确定性信息的有效方法之一,可以有效提高决策的准确性.当前,D-S证据理论在故障诊断[1]、模式识别[2]、目标决策[3]等多个领域得到广泛应用,在与不确定性相关的各种问题中,不确定性度量是至关重要的一步,它是定量研究信息不确定性的基础,可以用来解决冲突证据的组合问题[4].
为了解决D-S证据理论中不确定性度量问题,许多学者提出了不同的不确定性度量方法.具有代表性的两种不确定性度量方法是聚合不确定度(aggregate uncertainty,AU)[5]和多义度(ambiguity measure,AM)[6],但是这两种度量方法都是概率论中香农熵的推广,而不是在证据理论框架下的直接定义.也就是说这两种方法是把D-S框架下的证据经过概率转换得到一定的概率,然后计算相应的概率的香农熵来间接描述证据的不确定性程度.这种转化容易造成信息丢失,因此AU和AM存在对基本概率赋值(basic probability assignment,BPA)的变化不敏感等问题,这些问题的出现在一定程度上都与证据理论框架和概率论的框架之间的不一致性有关.证据理论并不是概率理论的简单推广,证据理论框架以信任函数理论为基础,信任函数不满足可列可加性[7],而可列可加性是概率论的公理化假设.
因此,在D-S框架下直接度量证据不确定性已成为研究热点.Yang等[8]提出了一种在D-S框架下总体不确定度(total uncertainty,TU)计算方法,然而该方法不满足不变性,即当识别框架变化后,不确定性也随之改变.Deng等[9]克服了Yang方法的局限性,提出了一种在D-S 证据理论框架下改进的总体不确定度(improved TU,iTU)度量方法.Li 等[10]提出了NTU(new total uncertainty measure)方法,该方法基于证据区间和最不确定区间之间的欧氏距离来度量总体的不确定性.Deng 等[11]基于海林格距离方法提出了DU(distance-based uncertainty)方法.上述几种方法都是在D-S证据理论框架下定义的,避免了D-S框架和概率理论框架之间的转换可能带来的信息丢失问题,然而这些方法在某些情况下会出现对证据的焦元或焦元质量变化不敏感的情况.
综上可知,解决不确定性度量问题的关键是直接在D-S证据理论框架下定义度量方法.由文献[8-11]所提方法的性质,可知一个好的度量方法应满足非负性、有界性、不变性、单调性、敏感性和低计算负担等性质,依据这些性质要求,本文首先提出了改进的归一化投影方法(improved normalized projection,iNP),并基于该方法,在D-S证据理论框架下提出了一种新的投影不确定性(projective uncertainty,PU)度量方法来度量证据的不确定性.对于给定的证据,本文使用每个单子集命题的信任函数和似然函数构成的证据区间与最大不确定区间之间的iNP来度量证据的不确定性.由于不需要在D-S证据理论框架和概率理论框架之间切换,因此该方法可以避免传统不确定性度量方法的局限性.最后基于PU方法给出了一种新的证据组合方法,通过目标决策仿真和Iris分类识别实例说明了该证据组合方法的有效性.
本文做了如下创新性工作:1)提出了新的改进的归一化投影方法iNP,给出了该方法的数学性质;2)在D-S框架下,提出了基于iNP的证据不确定性度量方法PU,理论证明和仿真实验说明了PU满足非负性、有界性、不变性、单调性、不反直观性、较高的敏感性和较低的计算负担等性质,这些性质保证了PU能够有效对不确定性进行度量;3)提出了基于PU的证据组合方法,并通过数值实例和实际应用,验证了本文所提方法的有效性.
2 基本概述
2.1 D-S基本理论
定义1(识别框架) 在证据理论中,一般用集合来表示命题,假设Θ表示一个互斥又可穷举元素的集合,则称此完备集合Θ为识别框架,即
由Θ的全部子集可构成Θ的幂集,记作2Θ,即
其中∅表示空集.
定义2(基本概率赋值(BPA)) 设Θ为识别框架,若函数m:2Θ →[0,1],满足: ∑A⊆Θm(A)=1且m(∅)=0,则称m为识别框架Θ下的BPA,m(A)也称为质量函数.对于∀A ⊆2Θ,m(A)表示对命题A的支持度,若m(A)>0,称A为Θ的一个焦元,所有焦元的并集称为核.
定义3(证据区间) 设m为识别框架Θ下的BPA,则命题A的证据区间为

图1 证据区间Fig.1 Evidence interval
定义4(Dempster组合规则) 设识别框架Θ下存在两个BPAm1和m2,Ai和Bj分别为m1和m2的焦元,当k<1时,Dempster组合规则为
其中k为冲突因子,即
Dempster组合规则也称为两个证据m1和m2的正交和,当k=0时Dempster组合规则没有意义.
2.2 3种投影方法
由式(3)知,证据区间可以表征对命题的未知情况,而证据区间可以作为一个区间数来处理,因此不确定性度量可以视为是两个区间数的相似性度量,下面介绍区间数的定义及其投影理论.
定义5(区间数) 区间数a可表示为
若a-=a+,则区间数退化为普通实数.设b=[b-,b+],当且仅当a-=b-,a+=b+时,a=b.
定义6(3种投影方法) 设a和b为两个区间数,则单向投影ProjS(a|b)、双向投影ProjB(a|b)[12]和归一化投影ProjN(a|b)[13]分别定义为
3种投影的区别在于单向投影直接给出投影值的大小,投影大小并不能刻画两个区间数的接近程度,例如设区间数a=[2,4],b=[1,2],由式(10)计算得,这表明ProjS(b|b) 定义7(聚合不确定度(AU))[5]m为在识别框架Θ下的BPA,则m的聚合不确定度为 其中概率分布p(θ)(θ ∈Θ)满足 定义8(多义度(AM))[6]m为在识别框架Θ下的BPA,则m的多义度为 其中BetPm(θ)为焦元θ的pignistic概率转换[14],即 其中|·|表示命题·的基数. 由上可知,AU和AM的不确定性度量实质上是把BPA转化为概率框架下的香农熵对其不确定性进行度量.然而,证据理论与概率论的理论框架不同,证据理论中的信任函数即使退化为贝叶斯信任函数(BPA的所有焦元均为单子集)也无法满足概率论中的公理化假设: 可列可加性[7],因此通过BPA转化为概率框架下的信息度量容易造成信息丢失(BPA的参数变化时,通过概率转化后,仍然得到相同贝叶斯转化结果的现象称为信息丢失),这将在第4节的例3验证. 定义9(改进的归一化投影方法(iNP)) 设a和b为两个区间数a=[a-,a+],b=[b-,b+],当a和b不为相等的实数时,改进的a向b上的归一化投影为 ProjI(a|b)具有以下性质: 1) 0 ≤ProjI(a|b)≤1; 2) 当且仅当a或b退化为实数时ProjI(a|b)=0; 3) 当a趋近于b(即a-趋近于b-,a+趋近于b+)时,ProjI(a|b)趋近于1,特别的,当且仅当a=b/∈R,ProjI(a|b)=1. 证性质1)-3)显然成立.证毕. 不确定性度量是证据理论的基础,直接关系到传感器的有效性判别,综合文献[8-11]所提方法的性质,可知一个好的度量方法应满足非负性、有界性、不变性、单调性、敏感性和低计算负担等性质.需要指出的是,不确定性度量并不满足传统度量空间的公理化定义(非负性、对称性和三角不等式),从而不是真正意义上的度量,而是一种广义度量. 定义10(投影不确定度(PU)) 设识别框架Θ={θ1,θ2,···,θn},m为Θ下的BPA,为θi的证据区间,则基于iNP的m的不确定性广义度量PU定义为 性质1 非负有界性.0≤PUΘ(m)≤|Θ|=n.其中当且仅当m为贝叶斯信任函数时,PUΘ(m)=0,当且仅当m为空信任函数(m(Θ)=1)时,PUΘ(m)=n. 注1PU的定义中没有采用归一化是因为归一化隐藏了系统的复杂性应与识别框架的基数有关这一基本特征,即基数越大,系统越复杂,不确定性的上界应该越大,如果采用了归一化,则不确定度范围限制在[0,1]中,这可能便于实际应用,但它隐藏了系统复杂性的信息. 性质2不变性.在开世界的条件下,设识别框架X=Θ+Θ1,其中Θ1={φ1,···,φk}是由新命题组成的集合,则PUX(m)=PUΘ(m). 证由于只是识别框架的扩张,m中的每个焦元的BPA没有改变,因此 因此 单调性的物理含义是: 证据理论中的不确定性度量不能在未知区间大(不确定性增加)的情况下,不确定性总量减小. 这引出式(21)成立,由式(21)成立显然引出式(22)成立.证毕. 性质4PUΘ(m)具有较低的计算复杂度. 证由式(18)可知,PUΘ(m)的计算只需要简单的内积、模和初等的代数运算即可,其计算复杂度为O(n),因而具有较低的计算负担.证毕. 性质5PUΘ(m)对于m的焦元或焦元质量的变化具有较高的敏感性. 性质6不反直观性.PUΘ(m)对于m的焦元或焦元质量变化时,不确定性度量结果不反直观. 性质5-6需要举例来说明. 例1假设识别框架Θ={A1,A2,···,A19},m为Θ下的BPA,m的各焦元质量如下: 其中Xt={A1,A2,···,At},α在[0.05,1]之间变化,t=1,···,19,m的不确定性PU度量结果如图2所示. 图2 t和α变化时PU的值Fig.2 The values of PU when t and α change 从图2可知,当t或α等于1时,此时m为贝叶斯信任函数,不确定度始终为0,当t=19,α=0 时,即m(Θ)=1,此时m为空信任BPA,不确定性达到最大19.从图2也可看到,图像具有一定斜率,没有出现(稍)平行于xy平面的部分,因此PU的度量结果对t和α的变化是敏感的,是符合直观的,这验证了性质5-6. 由于传感器自身的限制和环境噪声等因素的干扰,使得传感器测量的信息存在不同程度的不确定性.上节提出的PU方法可以对不确定性进行度量,在多传感器证据组合中,不确定性大的传感器证据权重小,反之亦然.基于这一思想提出基于PU的证据组合方法. 设在多传感器目标决策系统中,有N个传感器对某一目标进行识别,设识别框架为Θ={θ1,···,θn},N个传感器获得的BPA分别为m1,m2,···,mN,则基于PU的证据组合方法步骤如下: 步骤1由式(18)计算每个证据的不确定度PUΘ(mi),i=1,2,···,N. 步骤2确定每个证据的权重. 其中λ为调节系数.由式(26)知PUΘ(mi)与权重ω(mi)成反比,即不确定性大的证据权重小. 步骤3加权原始证据. 步骤4由式(7)对~m进行N-1次Dempster 融合. 其中mf是最终的融合结果. 步骤5做出决策. θtarget即为目标决策结果. 注2式(26)中调节系数λ的引入,是为了增加权重对不确定性的敏感程度,使得不确定性不同的传感器的权重具有较大差异,从而提升目标决策精度.λ越大对不确定性的抑制作用越明显.λ选的过小使得该方法过于保守,忽略了不同传感器不确定性的差异,λ也不宜选的过大,即使是不确定大的传感器也可能包含有用信息.λ的取值可根据实际情况进行选取,一般情况下λ可取5~10之间的数. 在第3.2节PU的单调性证明中知,PU满足单调性是因为iNP满足单调性,下面通过例2验证这一性质,并说明其他投影方法不满足此性质. 例2设区间数a=[α,β],其中α和β为变化的值,α∈[0,0.99],β ∈[α,1],当α和β变化时单向投影ProjS(a|MUI)、双向投影ProjB(a|MUI)、归一化投影ProjN(a|MUI),以及本文提出的ProjI(a|MUI)的变化结果如图3所示. 图3 区间数的4种投影Fig.3 Four projections of interval numbers 由单调性知,对于区间[α,β],当固定α时,投影结果应该随着β的增加而增加,固定β时,投影结果应该随着α的增加而减小,而在图3中,单向投影出现了当β等于1时,无论α为何值,投影值始终为1的情况,这显然不满足单调性,而双向投影和归一化投影,当固定α或β时,两者的度量值都出现了先增加后减小的情况,这显然也不满足单调性.在4种方法中,只有本文提出的iNP满足单调性,这说明了其有效性. 例3识别框架Θ={θ1,θ2},m为在Θ下的BPA,m的各焦元质量如下: 其中α,β ∈[0,0.5].分别计算α和β取不同值时5种不确定性度量方法AU,AM,TU,iTU和PU的值.仿真结果如图4所示. 图4 5种不确定性度量方法比较Fig.4 Comparison of five uncertainty measurement methods 从图4(a)可以看到,AU出现了信息丢失问题,这是因为,由式(30)引出 AU 计算证据的不确定度需要找到使香农熵最大的概率均匀的分布,又因为α,β ∈[0,0.5],所以p(θ1)=p(θ2)=0.5满足上述条件,因此不论α和β怎样变化,BPA概率转化结果始终不变,AU的值始终为1,AU出现了信息丢失的问题.AM同样出现了信息丢失的问题,这是因为,当α=β时,BetPm(θ1)=BetPm(θ2)=1/2,AM始终为1,这显然也是不对的.因为α=β=0不应该和α=β=0.5 的不确定性相等,α=β=0时,m为空信任函数,α=β=0.5时,m为贝叶斯信任函数,未知区间长度为0.综上AU和AM均出现了由于信息丢失造成的反直观的情况. 在证据理论框架下,TU,iTU和PU的度量结果如图4(b)-(d)所示.TU,iTU 和PU 均给出了α=β=0时,m的不确定性达到最大的结果.从式(30)可知,固定α,不确定度应该随着β的增加而减小,然而图4(b)中TU方法给出了不确定性先增加后减小的变化结果,出现了反直观的情况.iTU和PU的变化趋势符合预期,但从图4(c)中知当β从0.05向0变化时,iTU的度量结果过于平缓,变化不大,这说明了iTU存在对BPA变化不敏感的情况.从图4(d)知PU的度量结果均符合预期,说明了PU的有效性. 4.3.1 雷达辐射源证据组合 例4 以文献[15]中雷达辐射源识别为例,假设雷达识别数据库中有3个雷达型号数据(T1,T2,T3),即识别框架Θ={T1,T2,T3},现有5 个传感器m1,···,m5对某雷达辐射源进行识别,给出的BPA如下: 由第3.3节提出的证据组合方法计算得 1) 计算每个传感器BPA的不确定度. 2) 计算每个传感器BPA的权重. 其中取调节系数λ=10. 3) 加权原始证据. 4) 融合加权后的证据. 5) 决策目标结果为T1,支持度为0.9834. 同理,再分别基于2 个、3 个和4 个传感器,重复上述步骤,最终结果并与Dempster,Liu[15],Murphy[16],Deng[17]等人的方法进行对比,结果如图5和表1所示,从中可以看到使用Dempster组合规则对目标T1的支持度始终为0,这种反直观结果被称为一票否决悖论.Liu,Murphy,Deng和本文方法都得到正确的决策结果,相比于其他3种方法,PU在2-5个传感器的情况下的融合结果均对目标T1有最高的支持度,这是因为m2的模糊度较高,它的权重较小,因此PU能够快速识别出目标T1,这说明了其有效性. 表1 不同方法的证据组合结果Table 1 _Evidence combination results of different methods 图5 不同方法对目标对T1的支持度Fig.5 Support degree for target T1 by different methods 在表1的仿真中,取调节系数λ=10.当λ取其他不同值时,5传感器组合结果对T1的支持度如图6所示,从中可知随着λ的增加,对T1的支持度逐渐增大,这是因为减小了不确定性大的传感器的权重,使得向T1结果收敛的更快.同时也看到,当λ>10之后,实验结果的提高幅度变化不大,出现饱和现象,因此在表2的实验中,取λ为10.同时从图6也可知,即使取λ=1,对正确结果的识别率也能达到0.9501,其精度仍然高于Dempster,Liu,Murphy,Deng等人的方法. 表2 不同方法的融合结果Table 2 Fusion results of different methods 图6 λ变化时T1的支持度Fig.6 Support degree for T1 with the change of λ 例5 以文献[18]中5个传感器S1,S2,···,S5对空中识别目标为例.设识别框架Θ={A,B,F},其中A表示民用客机,B表示轰炸机,F表示战斗机,5个传感器给出的BPA如下: 应用本文提出的基于PU 的证据组合方法(取调节系数λ=5)并与其他方法(Dempster,Murphy[16],Chen[19],Yu[20]和Fei[21]提出的方法)进行比较,计算结果如表2所示,可以看到本文方法对正确结果{A}仍具有最高的支持精度,说明了本文方法有效性. 4.3.2 鸢尾花分类识别 例6在Iris数据集中,共包括3个种类的鸢尾花: Setosa鸢尾花(Se)、Versicolour鸢尾花(Ve)和Viginica 鸢尾花(Vi),因此识别框架为{Se,Ve,Vi}.每个种类的鸢尾花包含了50条样本,共计150条.其中每条样本含有花萼长度(sepal length,SL)、花萼宽度(sepal width,SW)、花瓣长度(petal length,PL)、花瓣宽度(petal width,PW)4种属性.随机从4种属性中各取40个数据作为训练集,每种属性其余的数据作为测试集,现从Se测试集中随机抽取一个样本(5.3,3.5,1.3,0.2)作为测试样本,对于该测试样本,文献[22]给出了4个属性BPA的测试报告,如表3所示.问题是融合表3中4个属性的BPA,判断花的种类.为了验证本文方法的有效性,使用AU[5],AM[6],TU[8],iTU[9],DU[11],以及本文PU方法分别计算表3中BPA的不确定度,取调节系数λ=5,计算结果如表4所示,再由式(27)-(29)可得融合结果如表5所示.由表4知,本文方法与其他方法大体一致,认为SW的属性的不确定性较高,PL的不确定性较低.由表5知,所有方法都高度支持Se,均能有效识别出花的种类,但本文所提出的方法对物种Se的支持度最高,说明PU方法具有较好的敏感性,具有快速识别目标的能力. 表3 样本的4个属性的BPA报告Table 3 BPA reports for four attributes of the sample 表4 不同方法的不确定度Table 4 Uncertainty degrees of different methods 表5 不同方法的4种属性组合结果Table 5 Combination results of different methods D-S证据理论BPA的不确定性度量有着重要的意义,它可以对传感器测得的数据的不确定性程度进行量化分析.为了解决这一问题提出了新的改进的归一化投影方法iNP,本文给出了其数学性质.然后,基于iNP提出了证据理论框架下,新的投影不确定性广义度量方法PU,理论证明和实验仿真验证了PU满足非负性、有界性、不变性、单调性、不反直观性、较高的敏感性和较低的计算负担等性质,这些性质保证了PU能够有效度量证据BPA的不确定性.最后给出了基于PU的证据组合方法.在仿真实例中,通过和其他文献的对比分析,说明了本文所提方法的有效性.作为本文的扩展,下一步将研究证据理论框架下,复数BPA的不确定性度量.2.3 两种概率框架下的不确定性度量方法
3 本文所提方法
3.1 改进的归一化投影方法
3.2 不确定性度量方法PU及其性质

3.3 基于PU方法的证据组合
4 仿真实例
4.1 iNP和其他投影方法的比较

4.2 PU和其他不确定性度量方法的比较
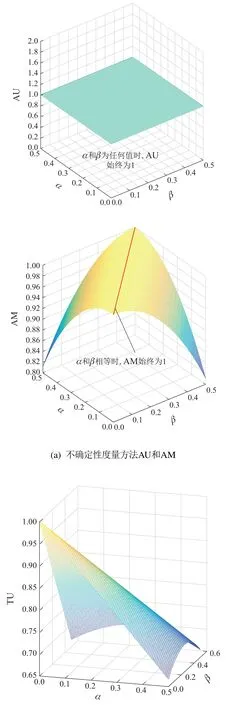

4.3 证据组合仿真实验
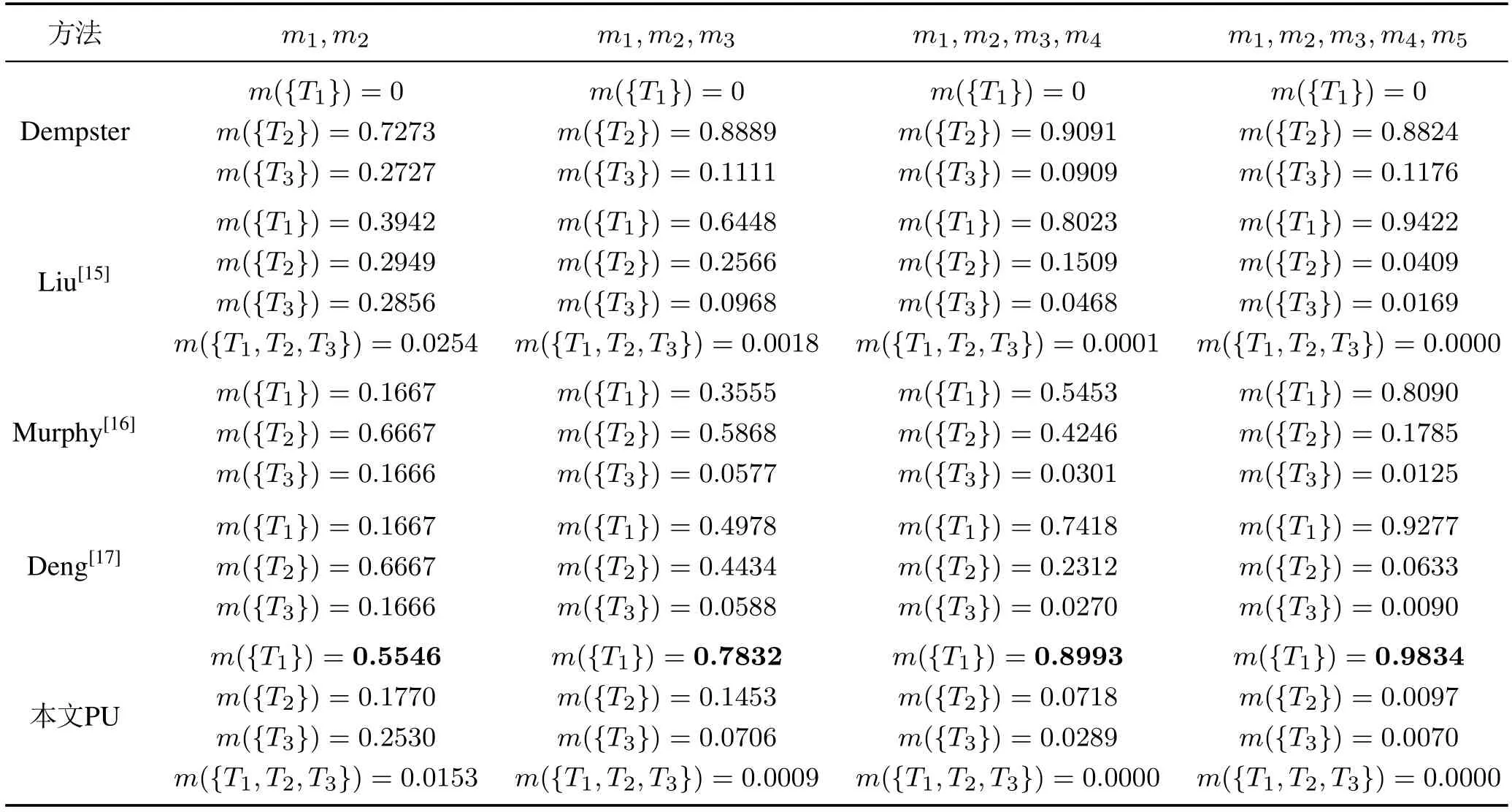
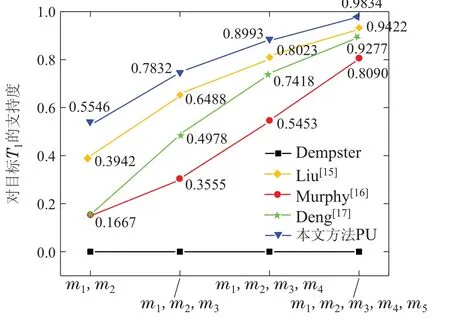
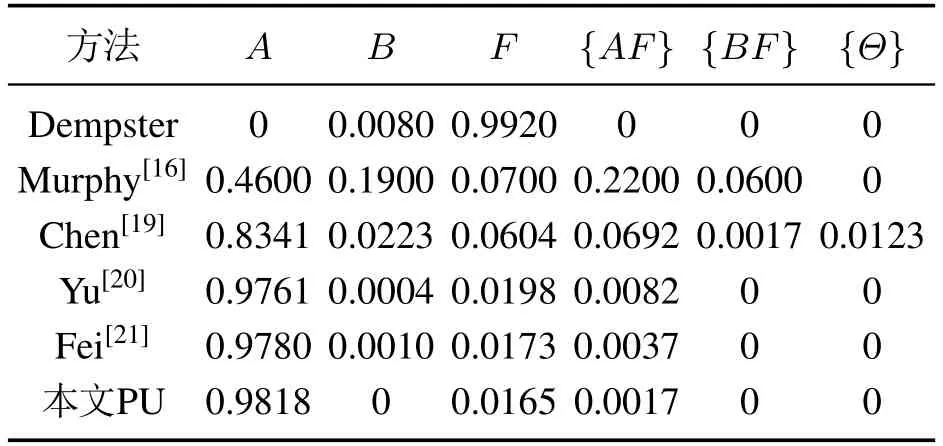
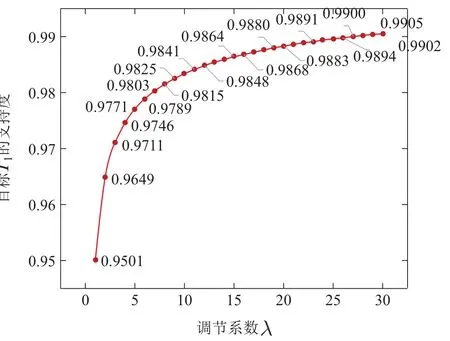
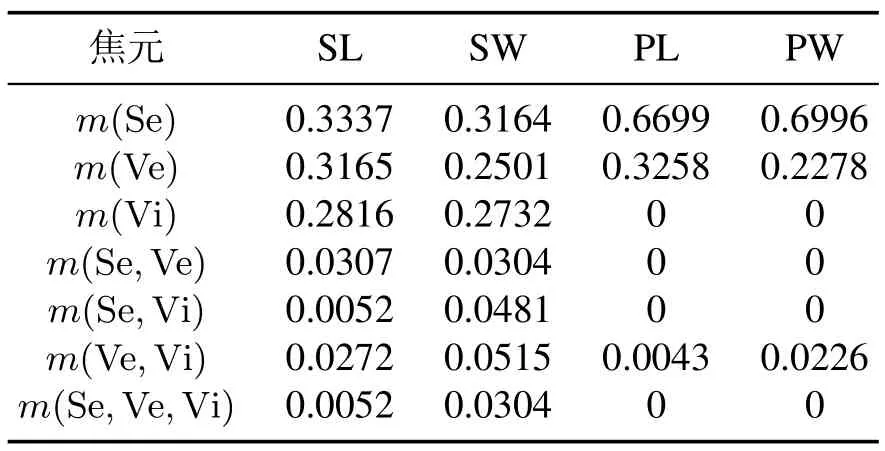
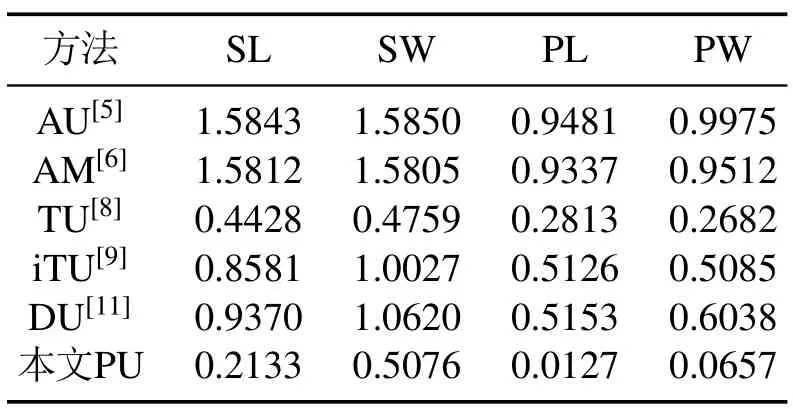
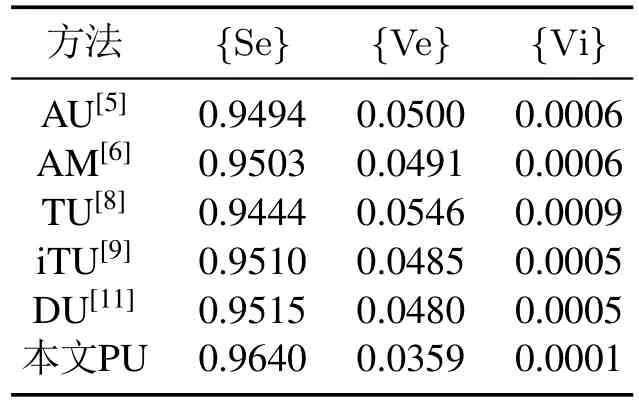
5 结论

