具有双储层结构的动态误差补偿回声状态网络
张昭昭,朱应钦,†,余 文
(1.西安科技大学计算机科学与计算学院,陕西西安 710054;2.墨西哥国立理工大学高级研究中心(CINVESTAV)自动化研究所,墨西哥城 07360)
1 引言
回声状态网络(echo state network,ESN)[1]通过观测时间序列数据来对动态系统建模,其主要特点是所需训练数据集和计算资源小,目前已在时间序列预测控制等领域得到了广泛应用[2-5].一般情况下,ESN通过最小二乘法或岭回归的方法最小化均方误差(mean squared error,MSE)来实现建模的过程[6].最小二乘法会导致输出权重估计剧烈波动,影响ESN的稳定性与建模精度,而岭回归方法虽然降低了估计方差,但该估计是一个有偏估计[7],不能保证ESN的建模精度.尤其在高阶非线性复杂系统中,由于误差自相关的原因,导致方差无法准确估计,这使得传统ESN 很难实现对高阶非线性复杂系统的精确建模.然而,大多数的工业过程是高阶非线性复杂系统[8],因此,构建能够对高阶非线性复杂系统精确建模的ESN模型是该领域研究的难点与热点[9].
近年来,国内外众多学者通过优化参数或结构的方法来提高ESN的性能[10-12].在参数优化方面,Chen等人[13]在灰狼优化算法的基础上,引入选择对抗策略来增加搜索能力.但由于储层结构生成的随机性,导致优化策略可重复性较差.文献[14]针对参数优化策略可重复性较差及算法效率低的问题,提出构建行为空间来确定网络结构是否具备优化条件以及后续优化方向,并结合新颖搜索遗传算法最终克服上述问题.然而,参数优化受到网络结构本身的局限,仅能逼近理论最优,也难以拟合高阶非线性复杂模型.文献[15]认为,由于常规储层计算难以产生多样化复杂动力学行为,仅仅依靠参数优化无法从根本上解决传统ESN不能应对高阶非线性复杂系统的问题.在结构优化方面,薄迎春等人从提高网络记忆容量的角度出发,提出时间分割池计算网络(temporally segregated reservoir computing,TSRC)[16]、稀疏连接的异步池计算网络(sparsely connected asynchronous reservoir computing network,SARC)[17]、异步深度池网络(asynchronously deep reservoir computing,ADRC)[18],通过延迟使网络具有不同时刻信息的记忆能力,最终提升复杂时间序列数据建模的能力.王磊等人[19]提出增量式学习回声状态网络模型(incremental regularized ESN,IRESN),根据问题复杂度或残差来设计合适大小的网络结构.然而,上述方法,无论是延迟深度网络还是增量网络,均是通过增加网络的深度和网络的个数来提升网络的性能[20],而网络深度和规模的增大无疑会导致网络学习成本的增加和网络稳定性的下降,且上述方法也未能针对常规ESN无法有效应对高阶非线性复杂模型从理论上进行分析.
本文针对常规ESN难以有效应对高阶非线性复杂系统的问题,通过理论与实验分析常规ESN预测高阶系统误差产生的原因,借鉴控制领域中采用动态补偿解决动态误差的思想[21-22],提出一种带有误差补偿机制的回声状态网络结构(error trace reservoir computing,ETRC).网络主要由计算层与补偿层构成,其中计算层初步构建(multiple superimposed oscillator,MSO)问题的数学模型,而补偿层则对由于计算层对期望方差估计不足而导致的幅值偏差进行补偿.最后基于人工数据和真实数据的实验结果表明,ETRC能有效降低误差之间的相关性,提升对高阶非线性复杂问题的建模能力.本文贡献主要在于: 1)理论分析回声状态网络误差来源以及当存在自相关误差时对网络稳定性的影响;2)提出一种新的储层计算结构,用于消除由自相关误差带来的影响,并证明其收敛性.
2 回声状态网络
2.1 ESN误差分析
经典ESN由输入层、储层和输出层构成,假设神经元节点数分别为K,N,L.拓扑结构如图1所示,其状态矩阵与输出矩阵更新如下:
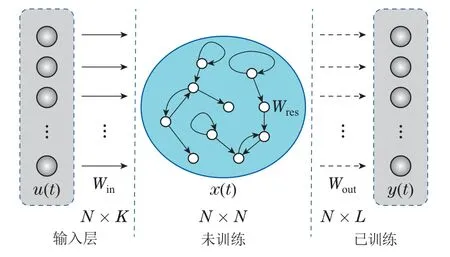
图1 ESN结构图Fig.1 Scheme diagram of ESN
记特征矩阵X=[x(1)···x(l)]T,特征向量X会形成一个N维特征超平面,对应的输出矩阵为Y=[y(1)···y(l)]T,ε为误差项.
回声状态网络的本质是训练向量Wout使特征矩阵X到期望输出矩阵Y之间距离最小,即估计最佳参数out来最小化均方误差(mean squared error,MSE)误差,如式(3)所示:
其中:M ∈RN×L,为真实值.常规最小二乘法(ordinary least squares,OLS)求解可得Mols=(XTX)-1XT;岭回归方法求解可得Mols=(XTX+λIP)-1XT;代入式(2)可得
根据式(4)可得偏差与方差的关系为
其均方误差如下所示:
优化均方误差面临的难题是现实中很难确定参数Wout和σ2,错误估计方差σ2与输出权重Wout均会增加MSE误差,从而使得网络预测性能不理想.目前针对ESN参数的确定大都采用元启发等优化算法,其实质是优化模型特征提取的能力,以此来保证输出权重Wout的准确性,但针对方差σ2却鲜有方法.因此,本文提出一种带有误差补偿的回声状态网络,采用补偿的方式尽可能的降低σ2估计误差,进而提高网络的性能.
2.2 回声状态网络自相关误差的影响
回声状态网络中常采用最小二乘法和岭回归的方法得到模型参数Wout.当满足基本假设时最小二乘法能够得到无偏估计量,但由于真实系统中误差et∈R存在自相关特性,难以满足正态分布et~N(0,σ2)和Cov(et,et-Δt)=0,∀Δt≠=0.但真实误差常具有自相关特性[23],如式(8)所示:
其中:ρ为不同时刻的相关系数,e为不同时刻的误差,τt为高斯噪音.由于误差与前一时刻常表现为高度相关,所以,本文将对一阶自相关误差et=ρet-1+τt的协方差进行推导.
et的方差为
根据式(12)可以得出,当存在一阶自相关误差时,若ρ=0.2,则Var(et)=1.042σ2,将会导致方差增大4%左右.最后结合式(10)-(13)求出协方差矩阵Cov(et,et-h)为
由上述证明可以得知,当存在一阶自相关误差时,Gauss-Markov假设不成立,即系统方差被低估,导致ESN预测的MSE增大.
3 误差补偿回声状态网络
3.1 ETRC网络模型
本文所提ETRC结构如图2所示,其动力学模型可表示为

图2 ETRC结构图Fig.2 The scheme diagram of ETRC
在ETRC中,输入与储层权重在初始化时随机给定并保持不变,仅需要通过学习确定,通常采用最小二乘法.本文所提ETRC网络由计算层和补偿层组成,构建ESN补偿层的理由在于: 1)由本文证明可知,储层计算过程中由于自相关误差导致Gauss-Markov假设不成立,使得预测误差增大.补偿层作为状态跟随器,可以实时补偿计算层输出,消除部分自相关误差,进而保证网络预测的稳定性.2)降低网络构建的复杂性.研究表明,针对复杂问题ESN短时记忆容量受神经元池规模限制[24].对长时依赖问题,需满足其最低记忆容量要求[14],通常采用构建大规模神经元池来提高网络记忆容量,但神经元池规模的增大会导致学习成本增加和网络稳定性的下降[25].ETRC采用一种分而治之的思想,计算层可认为是对预测信号的一次分解,补偿层用于拟合分解后的信号.将复杂的问题分解为难度较小的问题,最终降低网络构建的复杂性.
3.2 ETRC收敛性分析
引理1设ESN储层具有一个固定的内部权值矩阵Wres和f(x)=tanh(x).若内部权值矩阵的最大奇异值(W)<1,则ESN具有回声状态特性,使得=0,其中xk和是两个不同的状态向量.
定理1ETRC由两个ESN独立构成,若(W)<1,则具备回声状态特性.当误差存在自相关性且补偿层具备回声状态特性,存在ρ-→0,使得enew≤eregular,即.
证由式(8)代入可得
其中:eregular和enew分别为经典ESN和ETRC的误差,et为t时刻的误差,为t时刻补偿的误差,ρp为t-p时刻的相关系数,为补偿层学习得到的相关系数.所以当ESN具备回声状态特性时,存在(ρ1-)2≤,可推出enew≤eregular.显然,序列enew是递减的且有界为零,故ETRC收敛.证毕.
3.3 ETRC参数优化算法设计
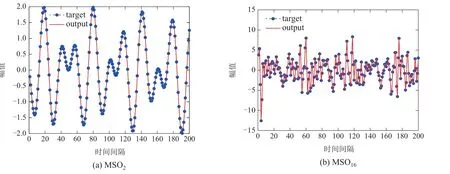
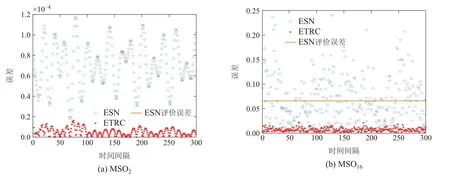
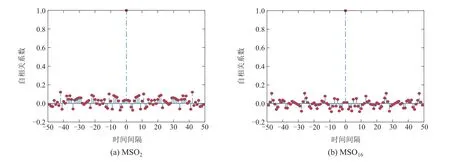
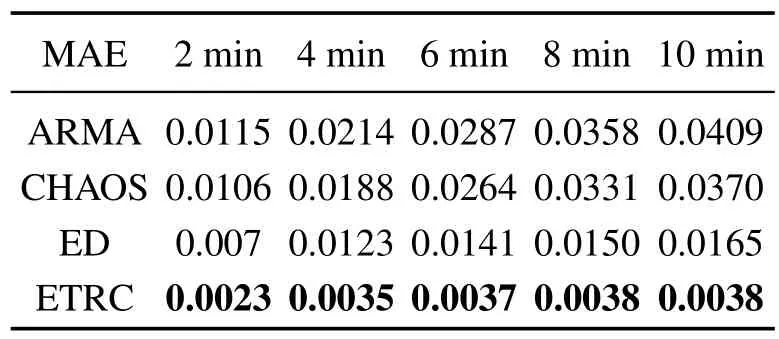
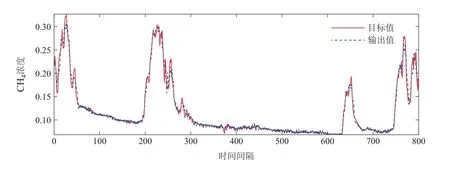
由于计算层对ETRC的性能至关重要,且计算层的性能影响着补偿层的预测精度,所以,对计算层进行优化尤为必要.从优化成本角度考虑,本文采用一种行为空间算法优化计算层,补偿层使用热重启的优化方法[26-27].行为空间是根据ETRC不同行为来评估网络质量的方法,其优势在于相对传统评判网络质量采用训练或测试误差,而行为空间则仅通过状态矩阵或少量训练即可评判性能好坏.热重启则是根据优化算法继续所消耗的期望时间E(Tcontinune)与重启算法E(Trestart)的期望运行时间关系来制定相应的策略.由于计算层已采用行为空间确定大致范围,所以补偿层仅需通过较少次数的随机初始化来寻找最优参数.其原因在于: 重启随机优化的期望时间远小于优化算法,即E(Trestart) 行为空间采用核心等级(kernel rank,KR)、泛化等级(generalization rank,GR)、记忆容量(memory capacity,MC)3个参数构建.核心等级与泛化等级用于评估储层特征提取以及泛化能力.记忆容量则评估整个网络的重现能力.具体构建方法如下: 其中:um为输入区间[-1,1]上均匀分布的随机信号;ym(t)为添加干扰信号后的输入,ym(t)=um(t)+z(t),z(t)∈[-0.15,0.05];x(um)和x(ym)为搜集不同输入所对应的状态矩阵. ETRC的记忆容量定义为 其中:yk(t)为ESN的第k个输出值,其对应的期望值为u(t-k);cov2和sigma2分别为协方差及方差算子.MC反映了ESN输出对输入信号的复现能力,MCk是yk(t)和的相关系数,为神经元个数.Jaeger等人[1]表示网络的记忆容量MC≤N,所以定义k的最大值为N. 由于行为空间能够表征储层性能的好坏,所以,采用该方法进行合理的筛选,可以有效的提升算法的性能.筛选策略分为初始化筛选与优化过程筛选两个部分. 初始化筛选是网络需要达到的基础条件,研究表明,当满足式(23)条件时[14],往往不具备预测的能力.依据网络行为空间的3个指标;KR,GR和MC,判断个体是否满足最低行为配置,其中:Si=0表示淘汰,Si=1表示保留.优化过程筛选则是根据训练误差判定具体的筛选标准.具体优化方法如下. 步骤1随机初始化P个不同参数的回声状态网络,计算泛化等级GR、核心等级KR、记忆容量MC这3个指标,以此构建行为空间.本文取P=75,输入权重和储层权重初始化范围为[-1,1]且服从均匀分布. 步骤2采用新颖搜索遗传算法对回声状态网络参数进行寻优,将式(24)作为遗传算法的适应度函数.并结合行为空间筛选机制(23)进行初次淘汰,最终采用最优参数进行预测. 其中:ξi表示与节点x相邻节点,dist(·)表示Euclidean距离.由式(24)可以看出,新颖性实质上是行为个体与k个最近邻个体之间的平均距离,所以,个体稠密区域则平均距离小,即新颖性低,反之,个体稀疏区域则平均距离大,则新颖性高. 步骤3将训练集样本分为训练集和校验集两部分,由步骤2可以得到初步的行为空间分布,继而采用误差搜索遗传算法,用于得到误差最低的解.并采用热重启生成20个符合条件当前行为分布的储层,作为补偿层的初始化参数. 步骤4将步骤2中最优模型根据式(16)计算训练误差E(t)=(e1,···,et),并作为补偿层训练集. 步骤5根据最终误差,从步骤3中20个个体中选择最优的一组作为补偿层参数. 步骤6由式(17)集成计算层与补偿层,并输入相应的测试数据,根据式(26)计算测试误差. 选择MSO问题对ETRC的动力学特性进行研究,主要考察神经元池能否存储多种频率的信息,MSO模型为 其中:Q为正弦波数量,α1=0.2+0.11(i-1).选择MSO问题主要有以下几个原因:1)针对常规储层计算难以解决MSO问题,缺乏相关文献分析其内在原因;2)MSO问题具有确定的动力学,有利于本文进行动力学分析.实验中采用规范化的均方根误差(normalized root MSE,NRMSE)作为测试误差指标,其定义为 其中:P为样本数量,为测试样本的方差,y和分别为预测输出以及目标输出. 图3所示为常规RC在针对MSO2,MSO5,MSO8,MSO12任务的误差自相关系数.从图3(a)-(b)可看出,当MSO维数较低时,网络与邻近时刻存在强相关性且呈现一定周期性.从图3(c)-(d)可看出,随着MSO的维数增加,误差自相关周期性规律逐渐消失,但误差仍然与前一时刻存在强相关.ESN学习过程中忽略了误差自相关性,导致预测误差增加.为解决以上问题,本文所提ETRC计算层用于尽可能逼近真实值,补偿层用于解决预测过程中可能出现的波幅预测不足与误差自相关等问题,其实质等同于式(8)数学模型.由于补偿层只对计算层的学习误差进行补偿,其复杂程度远低于计算层学习的原始任务,且网络的最终误差来源于补偿层. 图3 常规RC预测MSO问题的自相关误差Fig.3 Autocorrelation error of conventional RC prediction for MSO problems 本实验使用MSO2,MSO5,MSO8,MSO12作为测试模型,随着维数的上升,模型所包含的频率也随之增加.从图4(a)-(d)可以看出,针对相对简单的MSO2问题,ESN拥有较好的预测效果,但随着维数的上升,ESN的预测误差整体上升.观察误差走势可以看出,误差高的区域往往出现在数据波峰和波谷的区域.原因在于传统时间时间序列预测时,网络无法完全获得学习任务的全面知识,而学习任务新信息的引入导致神经网络预测产生偏差.所以,一个可靠的预测模型不仅应该包括数据点的预测,还应降低预测过程中不确定性对稳定性的影响. 图4 常规RC预测MSO问题的真实输出和误差曲线Fig.4 The real output and error curves of conventional RC prediction MSO problems 从误差曲线形态上分析,图4(a)误差曲线呈现出近似正弦形状,图4(b)-(d)也均近似于目标函数,但振幅远低于目标函数.上述说明,ESN特征超平面虽能够较准确的提取出相关信号频率特征,但由于各频率幅度较弱导致无法准确预测;另一方面,由于问题维数的上升,多种不同频率信号之间的叠加导致网络稳定性下降,而ESN本身的学习算法难以处理此类问题.本文引入补偿层的目的是降低由于原模型对新信息学习不足而影响系统的稳定性,其次,可以弥补计算层忽略的模型特征,从而提升预测精度和稳定性. 为进一步验证本文所提方法的有效性,分别将ETRC 与现有方法进行对比实验.包括常规ESN 网络、D&S RC(delay and sum readout reservoir computing)[28]、平衡回声状态网络(balanced ESN)[29]及TSRC[13].ETRC储层大小设置为200,经30次不同初始化的独立运行后,测试NRMSE的平均值如表1所示. 表1 不同ESN模型性能比较Table 1 Performance comparison of different models. 由表1可见,ETRC相较于ESN能够用于解决更复杂的MSO问题.随着MSO维数上升,误差补偿的优势逐渐体现,由于计算层预测误差增加,从而使得补偿层的效果更加明显.补偿层的添加弥补了计算层本身的不足,而对于复杂度较小的问题,由于计算层本身能够保证预测精度,且补偿层本身也具有误差,从而使得提升效果不明显.图5为ETRC针对MSO2及MSO16问题的测试效果. 图5 ETRC对MSO2及MSO16的预测效果Fig.5 The predictive performance of ETRC for MSO2 and MSO16 ETRC的鲁棒性定义如式(27)-(28)所示,其中:ei为测试误差;θ为阈值;ρ(θ)表示在M次测试中误差小于θ的概率;v(ei-θ)作为判断条件,0表示误差大于θ并剔除,1 表示误差保留并计算其概率.本文设定θ为计算层测试误差的平均值mean(erc)与最小值min(erc),用于研究添加补偿层后性能改善的效果. 图6为常规RC及ETRC训练时神经元池输出信号的差值.从图6(a)可见,针对MSO2和MSO16问题,当θ=mean(erc)的情况下,ETRC 较常规RC 优化率为100%.说明较常规RC而言,每一个预测点的精度均得到提升.当θ=min(erc)时,对MSO2问题的优化率仍为100%,但针对MSO16,问题优化率ρ(θ)=82.5%.图7表示ETRC预测误差的自相关系数分布图.从图7中可看出,误差与上一时刻不再存在强相关. 图6 ETRC与RC预测误差分布Fig.6 The error distributions of ETRC and RC 图7 ETRC误差自相关系数分布Fig.7 The error autocorrelation distributions of ETRC 误差补偿能够提升网络整体性能,首先是因为MSO2和MSO16的误差自相关问题均得到改善,其次是因为误差与原始信号频率特性相似,使得误差补偿的实质在于增强原始网络所捕获特征的强度.最后补偿层根据实际情况不断调整网络的误差情况,一定程度上提升了网络的稳定性.图6(b)可以看出,误差整体呈现下降趋势,且保证误差方差的稳定性.需要指出的是,虽然计算层和补偿层都具有误差,但其所需满足预测精度不同.相对于计算层需要精确预测,补偿层仅需满足趋势即可降低整体误差.如图8(b)所示,虽然预测精度降低,但仍具备不错的补偿能力.补偿层无法完全精确预测误差的原因在于,误差信号中包含了一部分白噪音信号,导致部分信息不可预测. 图8 ETRC补偿信号输出Fig.8 The compensation signal output of ETRC 实验数据采用石家庄某矿工作面4组不同区域的瓦斯浓度采样点数据,分别为进风口、上隅角、回风口、混合回风检测点,每间隔2 min收集一次数据.数据共记录2021-10-30 至2021-11-18 时间段数据,本实验采用18日12:12至18:12共6 h数据作为测试数据,其余数据作为训练数据集,测试误差为平均绝对误差 式中:m为预测样本总数,为真实值,yi为预测值. 从表2 中可以看出,在4 个监测点的预测任务中ETRC模型均表现出良好的预测性能.值得注意的是,随着预测步数的增加,网络在保证预测精度的前提下,预测误差仅在小范围波动.其原因在于随着计算层误差的增加,补偿层能够保持网络整体的稳定性. 表2 各监测点预测结果的平均绝对误差Table 2 The mean absolute error of the predicted results at each monitoring point 表3为将ETRC 模型与自回归滑动平均模型(auto regressive moving average,ARMA),混沌模型Chaos和长短期记忆网络(long short-term memory,LSTM)的编码-解码(encoder-decoder,ED)模型[30]进行对比实验.实验结果表明,本文所提ETRC模型对真实时间序列数据多步预测的有效性. 表3 3号监测点瓦斯浓度数据预测结果的比较Table 3 The comparison of prediction results of gas__concentration data in No.3 monitoring site 为了更直观的验证ETRC 模型的预测效果,图9-10给出了ETRC模型单步与多步的预测效果图.可以看出,ETRC对瓦斯浓度拟合较好.从误差分布可以看出,优化后低误差预测点个数增多,说明点预测处于高误差的概率明显低于优化前.但单步预测补偿效果略差于5步预测,原因在于预测步数增加使得计算层难以捕获全部有效信息,使得补偿层的作用愈加明显,进一步验证了本文所提误差补偿网络结构的有效性. 图9 监测点4瓦斯浓度单步预测效果图Fig.9 The performance of single step prediction gas concentration at monitoring point 4 图10 监测点4瓦斯浓度5步预测效果图Fig.10 The performance of five step prediction gas concentration at monitoring point 4 针对传统回声状态网络难以有效应对高阶非线性复杂模型问题.本文从自相关误差以及高阶模型不确定性两个影响预测性能的方向出发,在理论与实验分析的基础上,提出一种带有补偿的回声状态网络.在网络学习算法方面,采用行为空间与热重启的方法改善传统优化算法存在可重复性差以及优化效率低的问题.从MSO实验可见,ETRC框架能够有效降低由自相关误差与新信息所导致的不确定性,尤其对于高阶MSO模型的鲁棒性和准确性大幅提升.最后,采用石家庄某矿工作面4 组不同的真实数据进行验证,结果表明,本文所提ETRC 网络预测准确性高于其他网络,尤其是当预测步数增加时,ETRC网络预测精度相较于其他网络变化很小,证明了本文所提框架ETRC的有效性和稳定性.ETRC的模型本质是将误差反馈至计算层来提升性能,未来的工作是否可以估计输入数据和预测数据的概率密度分布,将其KL(Kullback-Leibler)散度作为预测误差反馈至计算层.改善计算层性能的同时,增加概率决策判定,仍值得进一步的研究.4 实验及分析
4.1 实验对象设置
4.2 预测MSO问题的自相关误差分析
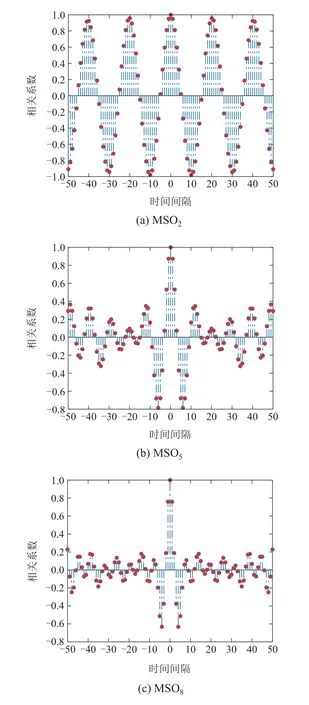
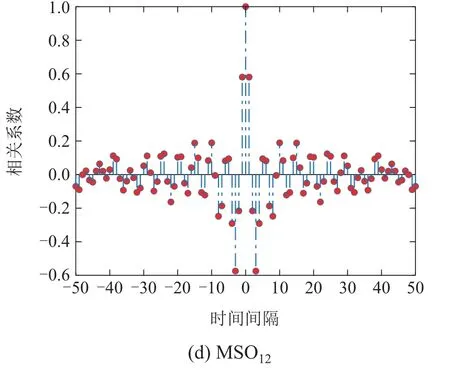
4.3 探究ESN无法预测高维MSO问题的原因
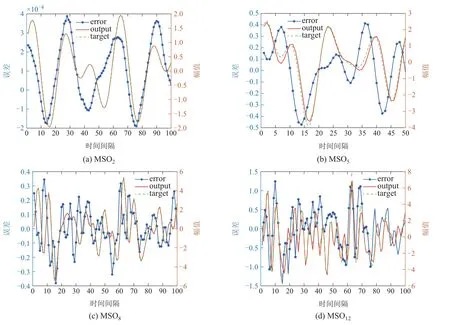
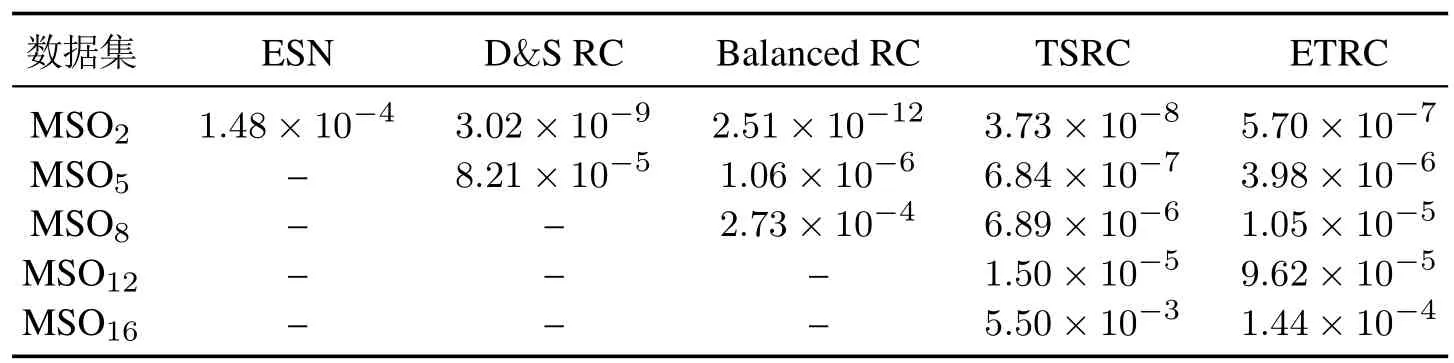
4.4 实验结果与分析

4.5 瓦斯浓度预测实验


5 结论
——北美又一种非常规储层类型

