多元纹理图像构造方法及应用

卢 明,王 程,谢永芳

(1.湖南科技大学 信息与电气工程学院,湖南 湘潭 411100;2.中南大学 自动化学院,湖南 长沙 410083)

1 引言

大量的传统图像处理算法仅能处理二维图像,如被灰度化或二值化的图像.对于一个像素具有不同测量值的多元图像,这类图像处理算法会忽略其多个通道间的关系.多元图像分析(multivariate image analysis,MIA)是一种由学者Paul Geladi于1989年提出的处理多元图像的算法,该算法可以对多元图像的多个变量进行分析[1].对于RGB图像,多元图像分析可以分析其颜色信息.多元图像分析将三维的RGB图像数据展开成一个二维的矩阵后,使用主成分分析法(principal component znalysis,PCA)进行分析,然后使用PCA分析的结果进行分割、分类、缺陷检测或预测.一些学者探索了MIA在多元统计过程控制中的应用[2],并将其应用于休闲食品工业[3-4]、定量视觉建模[5]和玉米缺陷百分比测定[6].随着MIA理论的发展,国内学者开始将MIA应用在工业领域:卢明等人[7]将多元图像分析技术在铜矿粗选方面进行了应用,并使用实验验证了其有效性;卢绍文等人[8]使用多元图像分析技术代替人眼,在电熔镁炉欠烧工况分类中对镁炉火焰进行特征提取.

纹理是图像的一种重要特征,在图像分割、特征提取等领域发挥着举足轻重的作用.而多元图像分析在图像展开的过程会丢失像素的空间信息,使得分析过程仅涉及独立的像素,未包含图像的纹理信息.为在多元图像分析中纳入图像的纹理信息,一些学者[9-11]提出了颜色-纹理图像分析法(color-texture MIA,ct-MIA),该方法将每个通道的图片向周围8个方向平移,叠加平移后的图像构造多元图像,然后再对构造的图像应用多元图像分析.ct-MIA 在钢材表面检测[9-11]和人造石缺陷检测[10]中进行了应用,实验显示,其相比MIA对图像纹理特征更加敏感,计算精准度更高.虽然ct-MIA尝试对图像的纹理特征进行分析,但采用像素平移的方法所体现的纹理特征较为单一,在背景复杂或纹理特征较弱的图像上应用效果并不理想.在数字图像处理领域被应用于处理纹理特征的另一种算法是灰度共生矩阵(gray level co-occurrence matrix,GLCM),其通过像素的强度和位置对纹理特征进行描述[12],在图像分割[13]、特征提取[14]和图像分类[15]等领域得到广泛应用.灰度共生矩阵充分提取了图像的纹理信息,但其忽略了图像多个通道间的联系,未利用图像的颜色信息.

应用多元图像分析进行图像分割有两种方法,分别是基于散点图和基于偏最小二乘法判别分析(partial least squares discrimination analysis,PLS-DA)的分割方法.基于散点图的分割方法使用多元图像分析得到主成分作散点图,对散点图上的聚类进行分析可以得到与感兴趣区域相关联的潜在空间;应用潜在空间于原始图像即可分割出感兴趣的区域,将潜在空间投射到新图像,也可以在新图像上完成感兴趣区域的分割[16].基于PLS-DA的分割方法则是联合潜在空间和感兴趣的得分图像构建PLS-DA模型,使用该PLS-DA模型对图像进行像素级分类,即可完成对图像感兴趣区域的分割[17].这两种方法均可以从图像上分割出某一类感兴趣的区域,但分割精度欠佳.

综前所述,ct-MIA分析的纹理特征较为单一,且进行分割应用时的精度不高.本文方法提取图像的纹理特征构造多元图像,对所得的多元图像应用多元图像分析方法得到得分图像,能分析图像的多种纹理特征,进行分割应用时分割精度较高.

为解决以上问题,本文的主要贡献是:

1)结合灰度共生矩阵和滑动窗口法提出了一种新的多元图像构造方法,该方法将RGB图像中的纹理信息概括为同质性、对比度、能量和相关性,并集成在构造的多元图像的每个通道中;

2)在本文提出的多元图像构造方法的基础上,结合多元图像分析方法进行图像分割应用,以综合图像的颜色与纹理特征对图像进行分割,提高分割精度;

3)在被油污污染的硅钢片图像数据集上进行仿真实验,实验结果表明,本文方法相比应用ct-MIA进行分割具有更高的精准度,且本文方法+决策树的分割方案也比ct-MIA+PLS-DA的分割方案计算精度更高.

4)在整个图像数据集上对本文方法与其他图像分割方法进行对比实验并统计实验结果,实验结果证明了本文方法的有效性与优越性.

2 基于图像纹理特征的多元图像构造

2.1 灰度共生矩阵及其统计

多元图像是一组在空间上对应一致的多通道图像数据,每个通道代表了同一个物体某种性质的测量值,这些测量值可来源于不同的测量方法,几乎所有的物理量均可以用来构建多元图像[18].本文使用灰度共生矩阵求取的纹理特征影像叠加以构建多元图像,所得的多元图像的每个通道均包含原始图像的某种颜色或纹理特征.

灰度共生矩阵是一种根据两个像素点灰度值关系出现的频率分布规律来阐述图像纹理信息的矩阵[12],被用于图像分类[19]、纹理提取[20]和特征提取[21].假设一张有限大小的图像,其水平方向具有Nx个像素,垂直方向有Ny个像素.Lx=0,1,···,Nx-1和Ly=0,1,···,Ny-1分别为水平和垂直空间域.灰度为i和j的一对像素点位置方向为θ,距离d的概率记为Pi,j(d,θ),具体表示如式(1)所示.

对二维图像上所有像素点求取Pi,j(d,θ),即可求得图像在某个方向的灰度共生矩阵.可根据灰度共生矩阵求取的统计量一共有14种,但其中大多数统计量相互关联,仅有4种统计量是独立的[22].因此,选取4种独立的统计量计算纹理特征影像即可求取图像的纹理特征.本文选择对比度、相关性、能量和同质性4种统计量用以计算纹理特征影像.

对比度反应了一张图像中每个像素与其周围像素强度的关系,纯色图像对比度为0,其定义如式(2)所示,式中的i和j为不同的灰度等级,p表示灰度共生矩阵中的不同元素.

相关性反应了一张图像中每个像素与其周围像素的联系,即纹理的相似程度,其值介于-1到1之间,纹理相似度越高其值越大.相关性的定义如式(3)所示,其中:µx和µy为灰度共生矩阵水平和垂直两个方向的均值,σx和σy为灰度共生矩阵在水平和垂直方向的标准差.

能量为灰度共生矩阵中元素的平方和,其反映了图像的清晰度和纹理的粗细程度,纹理越粗糙则值越大,如式(4)所示:

同质性度量了图像纹理局部变化的多少,图像局部纹理变化越小,纹理越均匀则其同质性越大,如式(5)所示:

本文基于灰度共生矩阵,以及以上4种统计量构造多元图像,下文将详述多元图像的构造原理与步骤.

2.2 纹理特征影像求取与多元图像构造

对于一张r×c×3大小的RGB图像,首先分离出其R,G,B通道图像,每张图像表现为大小为r×c的图像矩阵I,如式(6)所示:

步骤1以图像矩阵Ie的任一元素i(a,b)为中心,取其前后的行和其前后的列与其本身组成一个大小为n×n的矩阵W,n称为滑动窗口的尺寸,如式(8)所示:

步骤2为了能体现图像在不同方向上的纹理特征,所以需要求取矩阵W在0°,45°,90°和135°这4个方向上的灰度共生矩阵.

步骤3根据灰度共生矩阵算出矩阵W在4个方向上的对比度、相关性、能量和同质性统计量的值.然后求取每一种统计量的平均值,并以求得的平均值替换扩充矩阵Ie中的元素i(a,b).

步骤4重复第1步到第3步,直到对图像矩阵I中每一个元素执行上述操作为止.

经过以上4个步骤就得到了4个大小为(r+n-1)×(c+n-1)的统计量矩阵SCon,SCor,SEne和SHom.将求得的统计量矩阵与Ie相加,即得到了相应的纹理影像矩阵ICon,ICor,IEne和IHom,如式(9)-(12)所示:

上述4种纹理影像矩阵以图像形式显示即为纹理特征影像.以上步骤仅仅求出了RGB图像一个通道的4个纹理特征影像,对图像的剩余两个通道重复以上操作便求得了整个图像的纹理特征影像,一共12张图像.将图像的12个纹理特征影像按照R,G,B的顺序叠加得到多元图像X(r+n-1)×(c+n-1)×12,其构造过程如图1所示.由此方法构造的多元图像X具有12个通道,每个通道为原RGB图像的一种纹理特征影像,因此,构造的多元图像X的每个像素均具有12维特征.

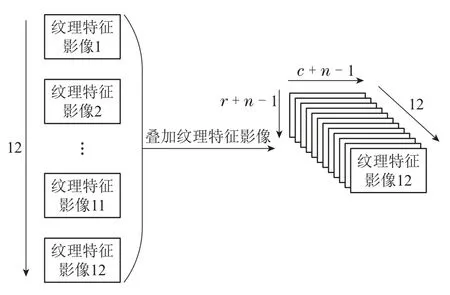
图1 多元图像的构造Fig.1 Construction of multivariate image

3 多元图像分析与分割应用

3.1 多元图像分析方法

PCA可以将多元图像数据分解成一系列相互正交的主成分,这些主成分是原始数据的线性组合,包含了原始数据的信息,按照方差从大到小排列.本文构造的多元图像X(r+n-1)×(c+n-1)×12具有12 个通道,在进行PCA分析前需要将多元图像数据展开成二维的矩阵.假设一个大小为(r+n-1)×(c+n-1)的单通道图像S的列向量为e1,e2,e3,···,er+n-1,则其可以展开成一个大小为((r+n-1)×(c+n-1))×1的列向量S′,如式(13)所示:

对多元图像矩阵X的每一个通道执行上式处理后合并到一个矩阵,则完成了多元图像矩阵的展开,得到展开矩阵X′,如式(14)所示:

多元图像每一个通道的像素数量即为展开矩阵X′的行数,多元图像的通道数量即为展开矩阵X′的列数.得到展开矩阵X′后即可对其进行PCA分析,将其分解成A(A≤12)个主成分的线性组合,如式(15)所示:

其中:ta(a=0,1,2,···,A)是相互正交,大小为((r+n-1)×(c+n-1))×1的分数向量;Pa(a=0,1,2,···,A)是相互正交,大小为12×1的载荷向量;E是大小为((r+n-1)×(c+n-1))×12的残差矩阵.

分数向量ta中的元素与多元图像中的每一通道的像素值一一对应,可以依照展开的顺序将其折叠成(r+n-1)×(c+n-1)的矩阵以恢复像素的空间信息,折叠后的矩阵以图像形式显示,被称为得分图像.使用两个不同的分数向量所画出来的散点图称为得分图,得分图像和得分图即可作为图像的信息用于分割.将载荷向量以直方图的形式呈现被称为载荷直方图,通过查看载荷直方图可以获知PCA对多元图像各通道的分析情况.

3.2 图像分割

图像分割目的是从图像中分割出感兴趣的区域,多元图像分析可以直接对一张图像进行分割,也可以对一种类型的图像进行分割.对于前者,从得分图中选择与图像相关的感兴趣区域的部分构造蒙版矩阵,即可对图像进行分割,也可以直接挑选最能突出感兴趣区域的得分图像利用阈值进行图像分割.在成功的分割图像之后,可以构建PLS-DA模型对图像上的像素进行分类,称为像素级分类.利用构建的PLS-DA模型可以对具有同类型感兴趣区域的图像进行像素级分类,将分类结果以图像形式显示即完成了对图像的感兴趣区域的分割.

使用PLS-DA模型对多元图像进行像素级分类准确度欠佳,对一些特征不明显的图像进行像素级分类会出现分类错误,如导致感兴趣的区域分割不完全或分割出背景部分.本文使用机器学习中的决策树对图像进行像素级分类,以完成对图像感兴趣区域的分割.决策树是一种使用对象的属性数据递归构建二叉决策树进行分类的机器学习算法[23].本文使用的ID3(iterative dichotomiser3)决策树学习算法以信息增益为准则来进行属性划分以生成决策树.假如一个随机变量X取值为X=x1,x2,···,xn,每一种取到的概率分别是p1,p2,···,pn,X的信息熵,定义如下:

根据信息熵的定义可计算得到信息增益,如式(17)所示:

其中:S为全部样本集合,valve(T)是属性T所有取值的集合,v是T中一个属性值,Sv是S中属性T的值为v的样例集合,|Sv|为Sv中所含样例数.

在完成图像感兴趣区域的分割之后,将分割出的感兴趣部分的值令为1,其余部分令为0.使用式(13)进行展开,作为决策树的训练输出数据.选择最能突出感兴趣区域的得分图像展开后作为决策树的训练输入数据.训练得到的决策树模型即可完成图像的像素级分类.

本文将使用第2节所述方法构造多元图像后,再使用多元图像分析进行阈值分割的方法称为GLCMMIA.

4 实验结果及讨论

钢铁工业中的无损检测系统会对硅钢条的表面缺陷进行检测,以把控产品质量.本节选用有缺陷的被油污污染的硅钢条表面数据集[24]作为实验对象,首先,以刮痕缺陷图像为对象进行图像分割并展示实验细节,然后,在整个图像数据集上进行实验,统计实验结果并进行分析.

4.1 图像分割实验

图像大小为640×480×3,图像上有反射伪缺陷干扰,如图2所示.选择缺陷为感兴趣区域,使用GLCMMIA对感兴趣区域进行分割.

图2 带有表面缺陷的被油污污染的硅钢条表面Fig.2 Oil-contaminated silicon steel pieces with surface defect

选择使用尺寸为9的滑动窗口,求取原始图像各通道的灰度共生矩阵的统计量矩阵,将其以图像形式显示即为灰度共生影像,如图3所示.

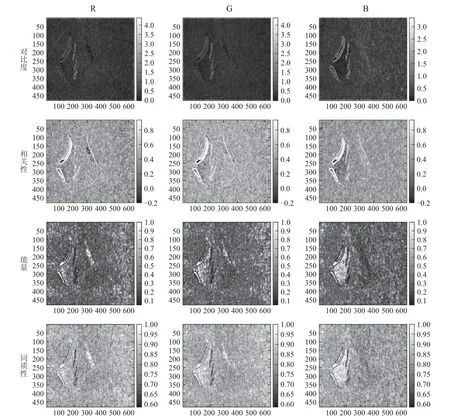
图3 灰度共生影像Fig.3 Gray-level co-occurrence image

第1行从左到右分别为RGB通道的对比灰度共生影像,其突出了表面缺陷和伪缺陷的边缘;第2行从左到右分别为RGB通道的相关性灰度共生影像,其硅钢条的刮痕像素强度与背景接近,伪缺陷较为突出;第3行从左到右分别为RGB通道的能量灰度共生影像,其刮痕和伪缺陷都较为突出,且刮痕与伪缺陷的像素强度相差较大;第4行从左到右分别为RGB通道的同质灰度共生影像,其突出了刮痕和伪缺陷的边缘.虽然这些图像都在一定程度上突出了刮痕,但是图像背景中散乱分布着大量与刮痕像素强度接近的像素点.

将得到的灰度共生影像与各通道的图像相加,得到纹理特征影像,如图4所示.

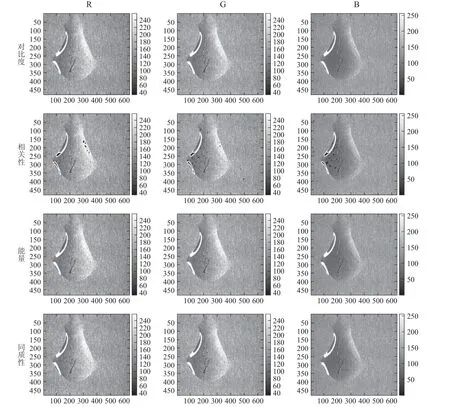
图4 纹理特征影像Fig.4 Texture feature image

纹理特征影像与图像各通道的图像相似,很难观察出显著区别.但纹理特征影像中同一物体的像素强度存在一定规律.使用PCA分析可以将这种规律具现.

将得到的纹理特征影像按照RGB通道顺序叠加,构造大小为640×480×12的多元图像.将得到的多元图像展开后应用PCA分析,得到分数矩阵.分数矩阵中前4个主成分的方差为99.9982%,包含了原图的主要信息.将前4个主成分以原图像的格式折叠,得到得分图像如图5所示.

图5 GLCM-MIA的得分图像Fig.5 Score image of GLCM-MIA

主成分(principal component,PC)中,PC1 的得分图像保留了原图的主要信息;PC2的得分图像突出显示了伪缺陷和刮痕,但二者的像素强度相近;PC3的得分图像突出显示了伪缺陷;PC4的得分图像突出显示了刮痕和伪缺陷,且二者的像素强度相差很大.

由此可见,PC1,PC2,PC3的得分图像中均存在着大量与刮痕像素强度相接近的像素点,若选择它们作为分割对象可能会存在一定的误分割,而PC4中刮痕像素强度与背景和伪缺陷的像素强度相差较大.因此,可选择PC4 的得分图像用作分割,使用阈值分割对PC4的得分图像做分割,得到分割后的图像,如图6所示.

图6 GLCM-MIA的分割结果Fig.6 Segmentation results of GLCM-MIA

对原图应用ct-MIA[8]得到的前4个得分图如图7所示.PC1的得分图显示了主要信息,PC2,PC3和PC4的得分图像突出显示了图像中的轮廓信息,但均未对刮痕,背景和伪缺陷做出区分.

图7 ct-MIA的得分图像Fig.7 Score image of ct-MIA

选择PC1和PC2作散点图,选择刮痕所在的集合做分割,得到分割后的图像,如图8所示.

图8 ct-MIA的分割结果Fig.8 Segmentation results of ct-MIA

为度量分割精度,此处使用均像素精度(mean pixel accuracy,MPA)和均交并比(mean intersection over union,MIoU)来衡量分割精度[25].为便于解释,做如下假设: 图像的像素共有k+1类,Pij为本应属于类i但被分类到类j的像素数量.MPA是每个类内被正确分类像素数比例的和的平均值,定义如式(18)所示:

MIoU是每个类的预测值和真实值的交集和并集之比的和的平均值,定义如式(19)所示:

GLCM-MIA 和ct-MIA 分割结果的性能指标如表1 所示,GLCM-MIA 的MPA 相比ct-MIA 提升了约15.31%,MIoU提升了约5.07%.

表1 GLCM-MIA和ct-MIA的分割性能表Table 1 Performance comparison between GLCMMIA and ct-MIA

研究载荷直方图可以得出每一个主成分所反映的不同颜色通道或纹理特性之间的关系.本文构造的多元图像包含了3个颜色通道,每个颜色通道4种纹理特征影像,共3×4=12种图像特征,GLCM-MIA的载荷直方图中的12个柱与这12种特征一一对应,载荷直方图中柱的长度与对应的特征在得分向量中的比重正相关,使用GLCM-MIA得到的载荷矩阵分别画出前4个主成分的载荷直方图.如图9所示.

图9 GLCM-MIA得到的载荷直方图Fig.9 Loading histogram of GLCM-MIA

分析GLCM-MIA的载荷直方图可知: PC1的载荷图中,12种图像特征的值都较为接近,因此PC1包含了原始图像平均的颜色特征信息和纹理特征信息;PC2的载荷图中,红、绿色通道特征为负值,蓝色通道特征为正值,且绿色通道特征的绝对值较小,因此,PC2着重体现了红色通道与蓝色通道之间特征的差异;PC3的载荷图中,红、蓝色通道特征为负值,绿色通道特征为正值,因此,PC3体现了绿色通道与红、蓝色通道之间特征的差异;PC4的载荷图中,每个颜色通道的纹理特征都有相似的分布趋势,即对比度纹理特征为正值,能量、同质性纹理特征为负值,相关性纹理特征的绝对值很小,因此,PC4体现了图像对比度与能量,同质性特征之间的差异,而GLCM-MIA的PC4得分图像中突出显示了刮痕,且与背景区别较为明显,PC4对于原图信息的提取实现了这种显示方式.

为研究PC4所提取图像信息的规律,建立PC4的得分图像中像素与其最邻近的8 个像素的强度图像,如图10所示.观察图10可知,PC4体现了右下到左上方向的像素强度变化.

图10 像素强度分布图Fig.10 Pixel intensity distribution grid

使用ct-MIA的载荷矩阵画出前4个主成分的载荷直方图,如图11所示.分析ct-MIA的载荷直方图可知:PC1包含了图像的平均颜色信息,PC2,PC3和PC4则提取了图像在某个方向的空间信息.

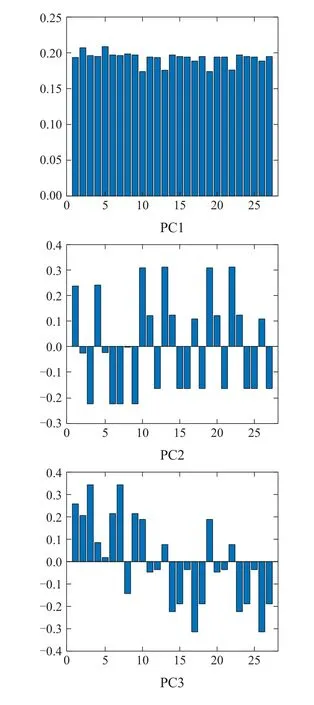
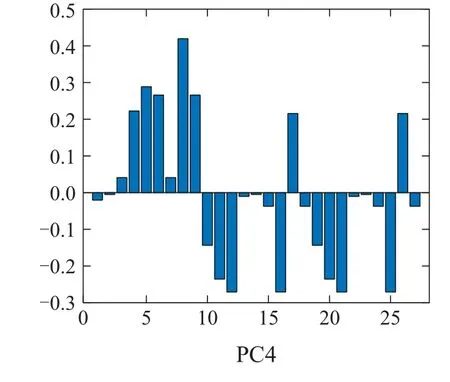
图11 ct-MIA得到的载荷直方图Fig.11 Loading histogram of ct-MIA

对载荷直方图的分析可知,GLCM-MIA 相比ct-MIA更能提取图像的颜色差异信息,且能提取更多的纹理信息.

使用前文的分割结果建立决策树模型,该模型可以对具有同类型刮痕缺陷的图像的像素进行分类,称为像素级分类.像素级分类会将图像的像素分成缺陷和完好两种类型,将分类结果以图像形式显示即完成了缺陷的分割.将GLCM-MIA 的得分矩阵的第4列作为决策树的训练输入数据,将GLCM-MIA得到的分割结果图像展开为(640×480)×1的列向量,作为决策树的训练输出数据,采用五折交叉验证,训练得到决策树模型.

使用训练好的决策树模型对具有同类型表面缺陷的被油污污染的硅钢条图像进行像素级分类.对该图像应用GLCM-MIA 进行分析,该图像及其第4得分图像如图12所示.该图像的第4得分图像同样突出显示了缺陷.选取对该图像应用GLCM-MIA后得到的得分矩阵的第4列作为模型的输入数据以完成像素级分类.

图12 原始图像与应用GLCM-MIA后的图像Fig.12 Original image and image after applying GLCM-MIA

分类结果如图13(a)所示,使用ct-MIA的结果建立PLS-DA 模型[26],对该图像进行像素级分类,结果如图13(b)所示.对比发现,应用GLCM-MIA进行像素级分类的结果分割出了一部分伪缺陷,但对于刮痕的分割相比ct-MIA完整很多.

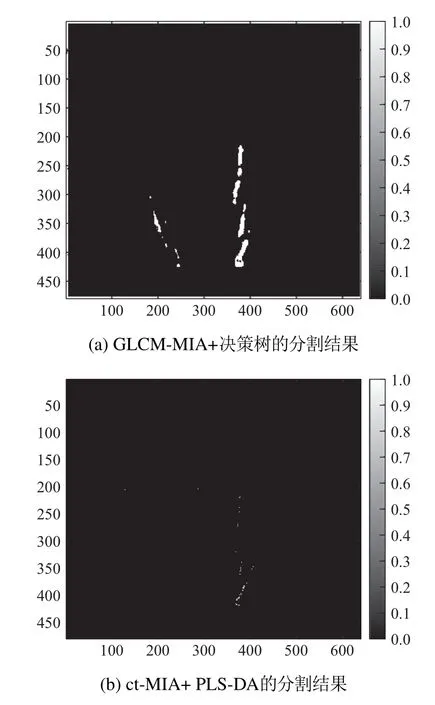
图13 不同方法进行像素级分类的结果Fig.13 Results of pixel-level classification using different methods

为量化应用GLCM-MIA 像素级分类进行分割的精准度,同样使用均像素精度MPA 和均交并比MIoU来衡量对图像进行像素级分类的精度.应用GLCMMIA和ct-MIA像素级分类的分割结果的性能指标如表2所示,从表中可以看出:GLCM-MIA 的MPA 相比ct-MIA提升了约23.23%,MIoU提升了约19.95%.

表2 GLCM-MIA+决策树与ct-MIA+PLS-DA图像分割的性能对比Table 2 Performance comparison of GLCM-MIA+decision tree and ct-MIA+PLS-DA

4.2 对比实验

在整个图像数据集上进行实验,数据集中包含硅钢条的常见缺陷的图像,即刮痕、小缺陷和擦痕,一共51张RGB图像,图像大小均为640×480×12.从数据集中选取3张具有不同缺陷的图像作为示例进行分割,选择感兴趣的区域为缺陷区域.3 种具有不同缺陷的硅钢条表面图像如图14所示,图14(a)-14(c)分别为具有刮痕、小缺陷和擦痕的被油污污染的硅钢条.

图14 具有不同缺陷的硅钢片Fig.14 Silicon steel pieces with different defects

本节选择与两种方法做对比,一种是ct-MIA[8];另一种是Guan等人[27]提出的一种基于峰值图的快速密度峰值聚类图像分割算法(peak-graph-based fast density peak clustering,PGDPC)相比一些图像分割算法具有一定优势.对比实验的实验结果如图15所示.

图15 对比实验结果图Fig.15 Comparison of image segmentation results

对图14(a)的分割结果如图15第1列图像所示,3种方法对于刮痕的分割都较为完整,但ct-MIA和PGDPC存在较多的误分割.对图14(b)的分割结果如图15第2列所示,ct-MIA对小缺陷的分割不完整,本文所提方法和PGDPC对于小缺陷的分割较为完整,但PGDPC存在较多的误分割.对图14(c)分割结果如图15第3列所示,PGDPC无法完成对擦痕的分割,ct-MIA和本文所提方法都分割出来了一部分的残痕,但是本文所提方法的分割结果更加完整.

为量化3 种分割方法的分割精准度,本节选择均交并比(MIoU)作为性能指标.ct-MIA,PGDPC 和GLCM-MIA性能指标如表3所示.

从表3中可以看出,本文所提方法对图14所示3张图像进行分割,相较于ct-MIA有3%～30%的性能提升.图14(c)中感兴趣区域与背景的颜色差异不明显,但具有一定的纹理特征差异,说明本文所提方法可处理图像的纹理特征;图14(a)-14(b)的背景较为复杂且有伪缺陷作为干扰,感兴趣区域与背景和伪缺陷有一定颜色差异,证明GLCM-MIA 也可对图像颜色进行处理.对数据集中的所有图像进行对比实验,统计ct-MIA,PGDPC和GLCM-MIA对3种类型缺陷进行分割的MIoU如表4所示.

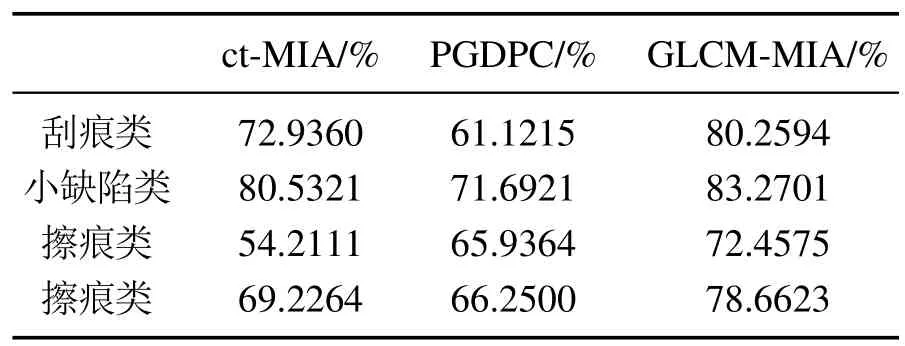
表4 性能对比表Table 4 Performance comparison table

综上实验结果与分析表明,本节提出的分割方法综合了图像的纹理特征和颜色特征,在分割精度上有一定优越性.

5 结论

本文基于图像纹理特征提出了一种新的多元图像构造方法,该方法构造的多元图像既提取了图像的颜色特征,也提取了图像的纹理特征.结合本文提出的多元图像构造方法与多元图像分析方法,进行了图像分割应用,解决了应用经典多元图像分析方法进行图像分割时无法分析图像纹理特征的难题.针对需要对多张图像进行分割的任务,使用GLCM-MIA与决策树结合,可以简化分割流程.在不同类型的图像数据集上进行仿真实验,实验表明,GLCM-MIA相比其他图像分割算法在计算精度上具有一定优越性.