计及多元不确定性的综合能源系统优化配置

周 帆,陈 龙,赵 珺,王 伟

(工业装备智能控制与优化教育部重点实验室(大连理工大学),辽宁大连 116024;大连理工大学控制科学与工程学院,辽宁大连 116024)

1 引言

随着物联网、人工智能等新兴互联网技术的快速发展,构建“能源互联网”成为改善传统单供系统缺陷的重要举措[1-3].作为能源互联网的重要组成部分,综合能源系统可实现多能互补及能量的梯级利用,在提高能源利用效率、减少污染排放方面具有显著的优势,已成为未来能源技术的重要发展方向[4-5].在考虑能源负荷需求、能源价格、设备参数的基础上,合理的优化系统的配置,包括设备的类型选择、连接关系等,是综合能源规划研究中亟需解决的问题[6-7].

目前,已有众多学者在综合能源系统的规划方面进行了大量研究[8-11],主要集中于系统的容量优化、选址优化等,采用的技术包括混合整数线性规划[12]、混合整数二阶锥[13]、多目标优化等[14].文献[15]采用混合整数线性规划方法评估系统总成本,包含设备成本、能源成本、维护成本与碳排放成本成本,并以此最小为目标,优化了某综合能源系统的设备选型与连接关系,且获得了系统在典型场景下的运行策略.文献[16]在充分考虑系统供用能特征以及负荷需求的情况下,研究了一种综合能源系统配置-优化算法,实现了系统的设备选型、容量规划与系统全年运行优化的统一求解.而在上述研究中,系统的供能设备连接关系大多预先设定的,并未考虑设备的选型、连接拓扑结构优化的问题.并且,其所针对的场景均为确定性场景,未考虑在光伏出力、负荷预测等方面的不确定性,从而会造成系统规划的方案过于理想化、设备的利用率低等缺点.为此,有学者进行了考虑不确定性因素的综合能源系统规划研究,其不确定性因素包括新能源出力预测、用户负荷预测等[17-19].文献[20]提出一种计及风光不确定性的综合能源系统两层级协同优化模型,其中,上层以年化总成本最低求解设备选型问题,下层以设备平均年利用率最高求解设备定容问题.文献[21]基于能源集线器模型,提出一种考虑冷/热/电多能负荷不确定性的综合能源系统规划方法,该方法通过K-means聚类方法获得多个典型日负荷场景,以上下界区间描述负荷不确定性,进而构建鲁棒优化规划模型.文献[22]以电-热-气多能微网系统为对象,考虑新能源出力以及负荷的不确定性,提出基于分位数梯度提升决策树的分位点-区间预测方法,并结合机会约束规划出力不确定性,提出考虑不确定性的来两阶段随机规划方法.然而,上述研究成果虽然考虑系统在负荷预测、光伏出力方面的不确定性,但缺少对系统运行阶段中面临的设备N-1不确定性[23-24]的考虑,使得规划的系统方案的供能安全能力具有局限性.

本文考虑综合能源系统在源-网-荷侧存在的不确定性,提出了基于多目标-机会约束规划的双层配置优化模型.上层以能源成本、环境成本、能源效率为目标,优化设计系统的配置方案,包括设备选型与连接关系;下层以年运行成本为目标,对于给定的一组方案,采用机会约束规划建立了系统在典型场景下的运行优化模型.考虑到可再生能源出力与用户负荷预测误差的不确定性,建立了满足置信概率的机会约束以描述能量的供需平衡.在模拟运行阶段,考虑到设备运行过程中不确定的发生故障,提出了系统调整裕度计算模型.进而建立了调整裕度与故障设备导致的能量缺额的机会约束,实现对各备选设备进行N-1检验.对于多目标优化模型获得的多组帕累托最优解集,以经济成本、环境成本、一次能源利用率、投资回收期为准则,采用信息熵与逼近理想排序法构建多准则评价模型,以确定最终的系统方案.以实际综合能源系统为研究对象,采用本文方法优化了系统的最优设备选型与配置数量,通过对比仿真,验证了本文方法的有效性与可靠性.

2 问题描述

典型的综合能源系统结构如图1所示.系统输入能源包括外购电能、天然气、太阳能与风能等多种形式介质,经由系统内所配置的变压器(transformer,T)、可再生能源发电(renewable energy generation,REG)、热电联产(combined heat and power generation,CHP)、燃气锅炉(gas boiler,GB)、电热泵(electric heat pump,EHP)、吸收式制冷(absorption chiller,AC)、电制冷(electric chiller,EC)等设备转换为用户所需的电、热、冷能源.同时,系统还可配置一定的电储能(electricity storage,ES)与热储能(heat storage,HS),以提升系统运行时的削峰填谷能力以及提高系统在峰谷平能源价格条件下的经济性.

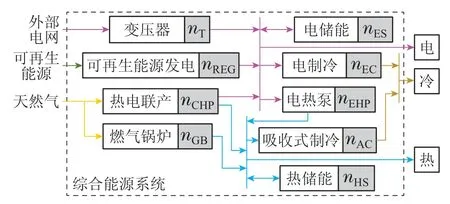
图1 典型综合能源系统配置图Fig.1 Typical configuration diagram of integrated energy system

由图1可知,系统中不仅包含多种类型设备,而且对于同一类型备选设备可配置多台机组.图中标注变量nd≥0,分别表示对应的备选设备的配置数量,d表示图中的各备选设备.当其值等于0时,则表示拓扑结构中不选择该类型设备;否则,配置nd数量的该类型设备机组.对于综合能源系统的配置优化问题,在考虑备选机组参数、能源价格、负荷需求等因素条件下,优化一组兼顾经济性、能效性与环保性的设备配置方案,向用户提供冷、热、电的能源.然而,在此过程中,对于用户的负荷需求、可再生能源的典型场景的出力,均需要采用预测的方式获得,然而对典型场景的负荷预测和可再生能源出力均存在误差.同时,对于给定的配置方案,受设备运行工况、部件寿命影响,供能设备在运行过程中存在不确定的设备故障问题.故此,针对由上述预测误差与设备故障引起的不确定性,在规划阶段如若能加以考虑,则会使得系统的供能方案能够更能满足实际需求,更具有实际的可行性.

3 计及多元不确定性的配置规划模型

考虑到综合能源系统在源-网-荷层面存在的不确定性,本文提出一种多目标优化-机会约束规划的两层优化配置模型.上层模型以经济性、环保性与能效性为目标,考虑备选设备的经济与技术参数,实现系统的结构优化.下层模型则以上层模型结构优化配置为边界,考虑到可再生能源出力与用户负荷预测的误差以及设备N-1的不确定性,以年运行经济性为目标,构建典型季节场景的模拟运行模型.图2为两层规划模型的逻辑框图.

图2 本文所提两层配置规划方法的逻辑框图Fig.2 Frame diagram of the proposed IES bi-level configuration planning method

3.1 上层配置优化模型

3.1.1 目标函数

1) 经济成本.

经济成本Ca以年为时间单位计算,主要包括年投资成本Cv、年燃料购买成本Cf及年设备维护成本Cm.对于图1所示的综合能源系统,外购能源为电与天然气.计算公式如下:

其中:D为备选设备的集合,d ∈D代表某一类备选设备;Nu表示一年中的典型场景数,u为场景的索引;Uu为场景u的持续天数;Tu为一天内的周期数,t为周期的索引;i为设备索引,Pd,i(t)表示其在时刻t的瞬时功率;BCHP,g(t)与BGB,g(t)分别表示热电联产与燃气锅炉消耗燃气的功率,Bg(t)则表示其总量;Be(t)表示购电的总量;分别表示热电联产的发电效率与燃气锅炉的产热效率;Vd,cd分别表示备选设备d的额定容量与单位投资成本价格;ce与cg分别表示外购电能以及燃气的单位价格;cd,m为设备d的单位维护成本;Δt为单位周期的持续时间,一般取1小时;ld表示该设备的设计寿命;CRF 为投资回报系数;r为投资年利率.

2) 环境成本.

环境成本以年碳排放成本Cce为指标,其作为最小化的优化目标加入到多目标优化模型中.计算公式如下:

其中:αe与αg分别表示电和燃气的碳排放系数,cce表示碳排放的单位价格.

3) 能源效率.

采用一次能源利用率作为系统能效的评价指标,衡量系统的能源转换效率.在系统规划阶段,应最大化该指标.其定义如下:

3.1.2 优化变量及容量约束

对于上层配置优化模型,通过优化各备选设备的配置数量,最终确定系统的供能配置.决策变量可定义如下:

对于集合D中的各备选设备,其配置数量需满足如下边界约束:

3.2 下层计及多元不确定性的模拟运行模型

本章节以年运行成本为目标,建立了基于机会约束规划的模拟运行优化模型,以使得系统能够以一定的置信区间消除源网荷不确定性的影响.

3.2.1 优化目标

下层模拟运行模型以最小化年经济成本为优化目标,用符号Cope表示,主要包含设备维护成本Cm、能源购置成本Cf与温室气体排放成本Cce.为降低计算的复杂度,采用典型季节负荷表示用户侧在全年内的能源需求情况.相应的计算公式可定义如下:

3.2.2 约束条件

本节优化模型的约束主要包括: 1)能源转换设备约束;2)储能系统约束;3)能量平衡的机会约束.

1) 能源转换设备约束.

能源转换设备可将输入能源转换成负荷需求的能源,如气-电、气-热、电-热、电-冷等.本文中,采用如下的的稳态模型描述设备对应的输入能源与输出负荷的转换关系:

其中:k表示能源种类,k ∈{e,h,g};ηc表示设备d的能源转换效率,表示该设备输入的能源,如电、热、气等.设备运行过程中,其负荷出力需满足容量约束

其中:Dc表示能源转换设备的集合,Dc ∈D,包括T,CHP,EHP,GB,EC,AC.Vd为相应设备的装机容量,与为设备的出力范围系数.

2) 储能系统约束.

对于储能系统设备,一方面其出力功率边界约束,另一方面,所具有的能源储量满足设备自身容量限制,如下式所示:

其中;i ∈ns,s ∈Ds;Ds表示储能设备的集合,包含ES与HS;ns为储能设备s的配置数量;Ps,i(t)表示t时刻第i个s储能设备的输出功率,若其值为正数则表示储能设备正在释放能量,否则表示设备正在存储能量;Ps,i,ch(t),Ps,i,dch(t)分别表示该储能设备的储能功率与释能功率;分别表示储能设备的储能、释能的最大功率边界;αs,i则表示相应的各储能设备的工作状态,1表示储能系统正在储存能量,0则表示系统正在释放能量.

为保证各储能设备的安全运行,在时刻t,其容量约束如下所示:

其中:Vs表示s储能设备的额定装机容量;Es,i(t)表示第i个s储能设备在t时刻的存储能量;ωs,w表示储能设备s的耗散率;ωs,ch与ωs,dch分别表示其储能效率与释能效率;与为设备的存储容量安全下限与安全上限.

3) 含源荷双侧不确定性的能量平衡约束.

为满足用户侧对电、热、冷能源的需求,对于系统中的某一设备,其能源供应形式可采用如下统一模型描述:

考虑到规划阶段对负荷及可再生能源出力预测误差的不确定性,本文中供需平衡约束以置信水平βb满足,如下式所示:

3.2.3 设备N-1不确定性检验

为保证系统的运行安全,系统规划阶段应考虑设备N-1故障.当设备发生故障时,该设备所提供的能量,可通过调节正常设备预留的调整能力来补偿,以降低设备故障对能源供应的影响.本章节中,上述补偿过程,以一定的置信概率满足.

在t时刻,系统所包含的能源发生设备与储能设备的调整裕度可定义如下:

其中:αs,i=0或1,表示t时刻设备运行在储能或者释能状态;分别表示能源转换设备与储能设备的调整裕度.特别的,由于光伏发电机组,其输出功率由环境条件决定,机组本身无法进行输出功率的调节,故该类设备的调整裕度为.本文中,为满足能源的供应平衡,当运行设备发生N-1时,根据正常设备预留的调整裕度,构建满足置信概率的调整裕度与能量缺额的检验约束,进而获得在满足N-1约束时的运行方案.

通过逐一对各设备的N-1状况进行检验,判断当前配置方案是否通过N-1检验.

其中:f ∈nf,f为异常设备的序列,nf为其对应的配置数量,αf=1表示该设备发生N-1故障;ef(t)为供能缺额不确定性随机变量,βf为置信水平.

3.3 机会约束的转化与规划模型求解

3.3.1 机会约束的转化

为求解所构建的双层规划模型,需要将机会约束转换为确定的约束条件.对于式(24)所示的供需平衡概率约束,为便于研究本文假设可再生能源出力与负荷预测偏差均服从正态分布

则式(28)做如下转化:

成立.因此,上述机会约束可进一步转化下式中的确定性约束:

其中ϕN表示标准正态分布的分布函数.

本文假设能量缺额的不确定性随机变量亦服从正态分布.ef(t)～N(µf,),则式(27)可转化为如下确定性约束:

3.3.2 模型的求解

如上述分析,本文上层配置优化模型为多目标优化模型;下层模型由于考虑了储能设备的运行状态,在将机会不确定性约束转化为确定性约束后,可转化为混合整数非线性规划问题.

对于多目标优化问题,该类问题的最优解是一组Pareto最优解集.非支配排序遗传算法(non-dominated sorting genetic algorithm-Ⅱ)[8]方法降低了非劣排序遗传算法的复杂性,具有运行速度快,解集的收敛性好的优点,成为其他多目标优化算法性能的基准.鉴于此,本文采用该方法求解上层配置优化模型.

而对于转化后的混合整数非线性规划模型.本文采用商业优化求解器Gurobi[15]进行求解,可优化获得系统在典型场景下的最优运行策略.

3.3.3 多准则综合评价

对于多目标方法获得的Pareto最优解集,本文采用信息熵[20]与逼近理想排序法[21]相结合的方法构建综合评价模型,以确定最终的配置方案.

假设有m种备选方案,假设建立了n种评价指标,则经过计算,可获得评价结果矩阵,用符号H表示.

其中hij表示第i种方案的第j个指标的计算结果.本文综合能源规划研究旨在获得综合评价值最大的方案,需要将各指标标准化.对于最小化类别的评价指标,采用式(33)标准化;反之,则采用式(34)标准化计算:

基于获得各方案的指标值,本文采用信息熵方法获得各指标的权重矩阵.该方法根据数据本身客观的差异性确定指标的权重.采用该方法获得权重可表示为w=[w1w2···wn].更进一步,采用逼近理想排序法构建综合评价模型,如下式所示:

其中:Ei表示第i组准则的综合评价结果,且0≤Ei≤1;表示第i组准则距离最大值的距离,而则表示与最小值的距离.对于综合评价结果Ei值越大,则表示被评价方案越接近最大值,表明该方案从综合评价的角度分析是最优的.

4 案例分析

4.1 案例说明与参数设定

本文以国内某综合能源系统为研究对象[15],能源供应关系可抽象为图1所示.该综合能源系统为国内某市的智慧社区示范项目,需求负荷的类型包括冷、热、电3种能源.该社区建筑面积为0.1平方公里,容纳1500人.全年的天数设定为365天,各场景的持续时间分别为:春季场景为90天,夏季场景为93天,秋季场景为90天,冬季场景为92天.此外,典型的可再生能源发电设备有光伏发电(photovoltaic,PV)与风力发电(wind generation,WG),然而由于项目的地区不是典型风场,系统规划时,可再生能源发电设备仅考虑光伏发电.

本文电价采用峰-谷-平分时电价,峰时电价为0.18$/kWh,平时电价为0.132$/kWh,谷时电价为0.072$/kWh.天然气价格为0.0392$/kWh.冷、热负荷收益单价为20$/GJ.电力与天然气的粉尘排放系数分别为0.968与0.22 kg/kWh.碳税价格为0.0032$/kg.外购电能假设由传统火力发电方式产出,其发电效率取0.48.实验过程中,负荷需求、各备选能源设备的技术与经济参数可参考引文献[15].不确定性随机变量假设其服从高斯分布,均值为0,标准差为负荷值的10%,置信概率取值均为95%.NSGA-Ⅱ的种群数量设置为50,交叉概率为0.9.

4.2 实验结果与分析

在置信水平为95%的条件下,采用本文所提考虑多元不确定性的双层配置方法所获得的方案如表1所示.表2为各方案相应的经济性、碳税与能效指标结果.由表1-2可以看出,不同的方案对于经济性、环保性以及能效方面的表现具有显著的差异.方案#1相比于方案#2,虽然在经济成本与能效方面优势较弱,但其能够有效降低碳排放,在环境保护方面优势明显.方案#5相较于方案#4,其能源利用率水平非常高,但是该方案对经济成本依赖较高,同时在碳排放控制方面也表现较差.而对于方案#8,该方案在控制碳排放方面表现最优,但对投资经济性的依赖也是最显著的.

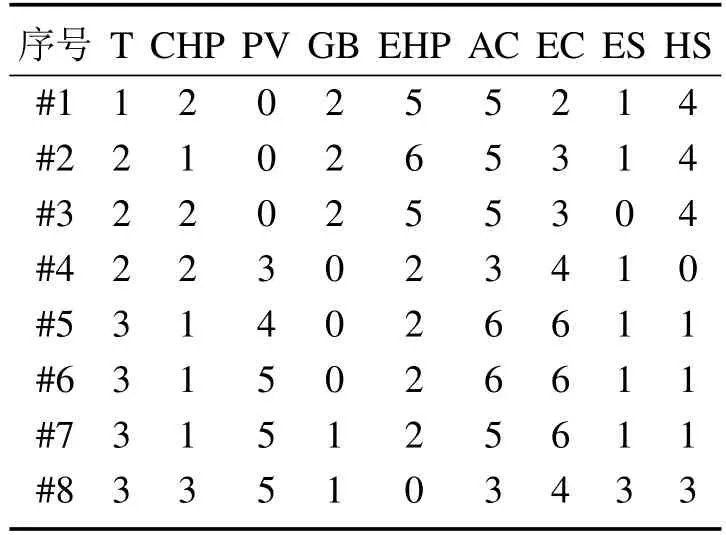
表1 采用本文方法所获得的帕累托解集Table 1 Pareto front sets obtained by the proposed method

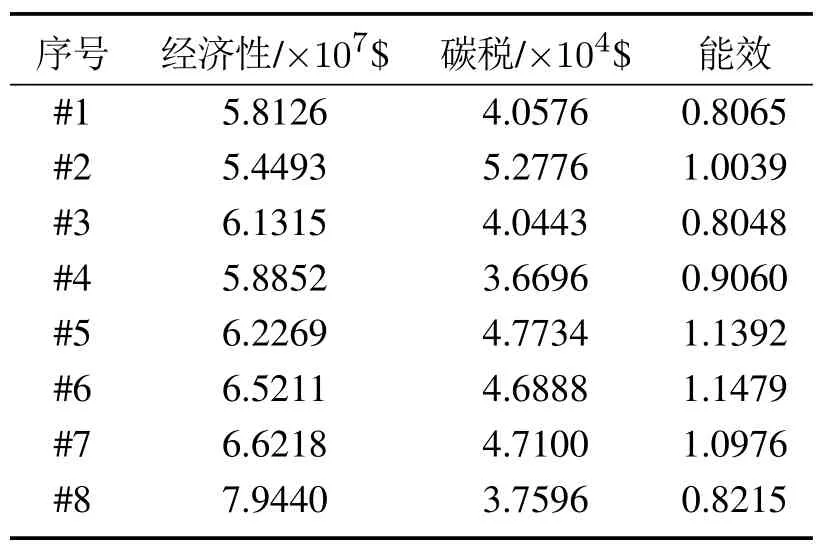
表2 所获得的帕累托最优方案及优化目标值Table 2 Alternative schemes and the corresponding objective values of the Pareto front sets

为确定最优的系统供能结构,本文选择设备购置成本、年运行成本、碳税成本、一次能源利用率以及投资回收期构建多准则评价指标体系.采用信息熵-逼近理想排序法相结合的多准则评价方法实现各方案的综合评价,并以综合评价最大的方案作为最终的规划方案.各准则值、确定的准则权重以及综合评价的结果如表3所示.

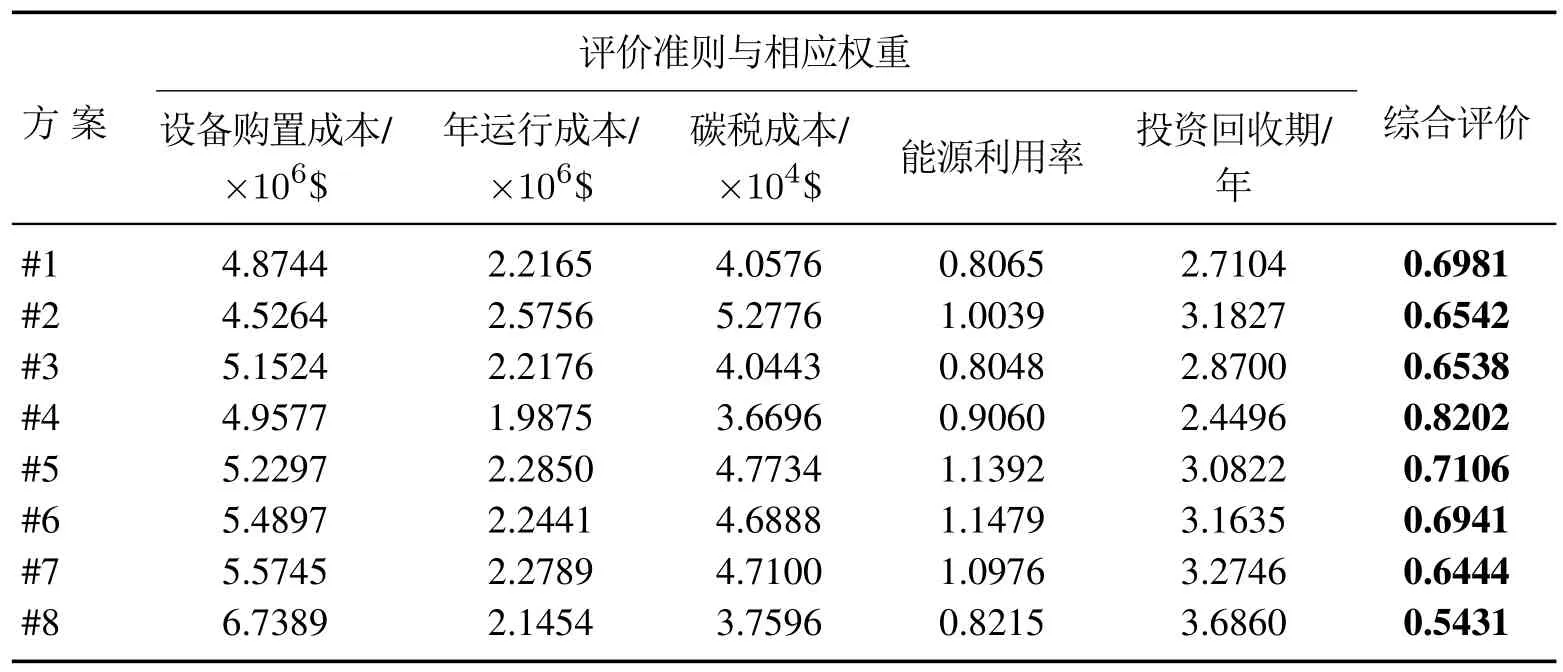
表3 本文所获得的各方案的综合评价结果Table 3 Comprehensive evaluation of the configuration schemes using the proposed method

从结果来看,设备购置成本、碳税成本、一次能源利用率与投资回收期评价准则的重要程度高.从综合评价的结果来看,方案#4,虽然其能效水平不是最优方案,但其余各项评价准则均处于最优或次优状态,且该方案具有最高的综合评价结果.方案#1,#2与#3配置了较多数量的GB与EHP,在满足用户侧热负荷条件下,提供了富余的热能;同时,系统则利用HS与AC配合实现能量的梯级利用,有效降低了设备购置成本,在投资回收期方面比较有优势;然而,由于外购电能以及GB在环保方面优势较弱,使得系统的碳排放控制表现较差.方案#2,#5,#6与#7配置了数量多的高能效的EHP与EC设备,使其能效表现较优,均超过了100%;但由于其CHP设备的数量较少,系统运行时对外购电能的需求较大,导致方案在碳排放控制方面效果不佳.对于方案#8,系统配置了多台CHP以及PV,降低了系统对外购电能的依赖,使得系统的碳排放控制表现最优.同时,在考虑峰谷平电价条件下,由于储能系统的配置可实现能源在时间层面的转移,可有效改善系统运行的经济性,但由于系统建设投资成本较其他方案较高,使得系统的综合评价处在较低水平.结果表明,基于本文构建的综合评价模型可最终选定方案#4本文的规划方案,表明了本文所提规划方法的有效性.

4.3 典型场景的运行策略

对于给定的配置方案,下层优化模型可获得在典型场景下的运行策略,结果分别如图3-5所示.图中曲线表示典型场景的用户侧负荷曲线,彩色柱状图表示对应设备的出力功率.

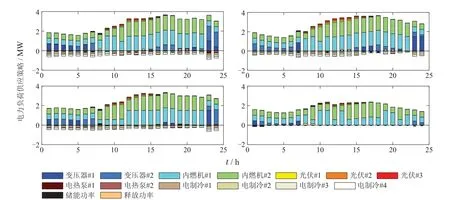
图3 不同场景下的电负荷供应策略Fig.3 Power supply strategies in multiple scenarios

由图3可知,考虑到峰谷平分时电价政策,在夜间谷时电价时,CHP处于低功率运行,电能供应平衡多通过外购电能满足;在峰时与平时,两台CHP均是高功率运行,其在提供电能的同时,也可实现能量的梯级利用,向系统输出热能.同时,本文配置两台变压器设备,实现1用1备,用于保证系统电能供应的安全.

如图4所示,系统所需的热能主要来源为CHP的余热.为了保证热网的削峰运行,本文配置了两台EHP机组,设计为1用1备,以满足热能供应时的N-1安全等级.对于热网在满足用户负荷需求后,富余产出的热能量则通过AC机组,将高品位的热能转化成低品位的冷量.

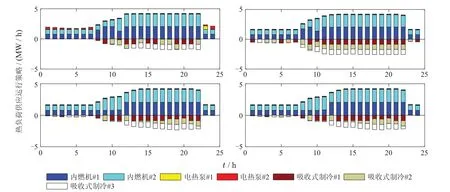
图4 不同场景下热负荷供应策略Fig.4 Heat supply strategies in multiple scenarios

图5为系统冷量供应时的设备运行出力.由图可知,3台AC机组将热网富余的热能转化为冷量,向用户侧提供冷能.4台EC机组,运行模式为3用1备,3台机组协作运行,与AC制冷机组配合满足用户需求.尤其是夏季日间冷量需求高的情况,3台EC机组需要全开,才能满足用户的冷需求.

图5 不同场景下冷负荷供应策略Fig.5 Cool supply strategies in multiple scenarios

由上述分析可知,基于本文方法获得设备配置,不仅能够满足系统的供能需求,而且在规划时考虑了多元不确定行,尤其是设备的N-1不确定性,使得系统的能源结构在供需过程中具有更高的安全等级.

4.4 与传统规划方法对比

为更一步验证本文方法所规划方案的有效性,本文采用文献[15]中所提出的以经济性为目标的混合整数线性规划(mixed integer linear programming,MILP)方法进行对比实验分析.该方法以总体经济性最小为优化目标,包括设备投资费用、运维成本与环保成本,旨在获得经济性最优的配置方案.

表4是采用MILP方法获得配置方案以及对应的各计算指标值.由结果可知,2台CHP作为供热的主要设备,满足用户侧负荷的热需求.对于CHP和PV无法满足的电负荷,则通过1台变压器由外电网采购.为保证热网的运行稳定,规划模型从经济性角度,配置了2台HS设备,用于热网系统的削峰填谷运行.冷负荷则由3台AC机组与3台EC满足,AC机组将热网富余的热量转化成冷量,一方面保证了热网稳定运行,另一方面减少了EC出力.

表4 基于MILP获得经济性最优的配置方案Table 4 Economic optimal configuration scheme obtained by the MILP algorithm

相比于传统方法,本文所提方法重点考虑了系统的多元不确定性,尤其是N-1故障.本章节选择各场景12时刻的能源需求,以1台CHP发生故障为案例,计算各场景的能源缺额,旨在可通过调节正常运行设备的预留容量实现N-1设备的出力功率值的补偿.如果当前设备预留的容量可将N-1设备的出力补偿,则表明系统可通过改变供能结构,继续满足能源平衡供应.否则,则表明系统无法实现满足能源供需平衡.且缺额越大,表示系统对于N-1故障的应对能力越弱.由于CHP设备属于热电联产设备,表5统计了在冷负荷供应不变的条件下的电能、热能的缺额.

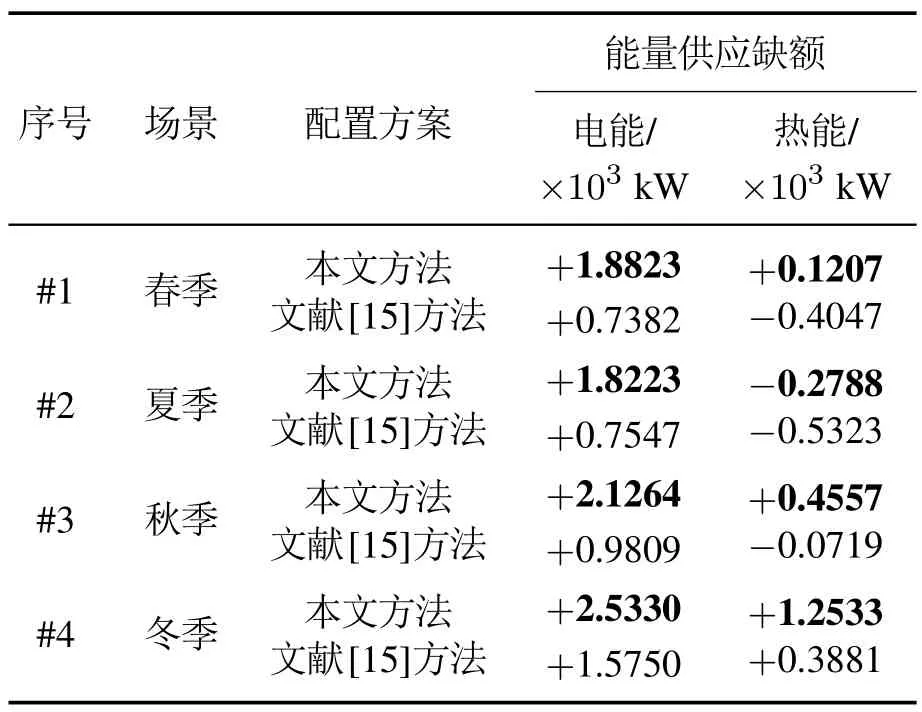
表5 各场景中热电联产设备故障时的供能缺额Table 5 Energy gap for each scenario in the event of CHP equipment failure

由表结果可知,在1台CHP发生故障时,基于本文方法的供能方案,能够更好的通过调节正常工作设备的调整裕度,保证供能平衡.在电能供应方面,两种方案中均有一定的富余调整度,而对于热能供应,基于MILP方法获得方案在春季、夏季、秋季均出现一定的能量缺额.特别的,在夏季场景中,本文方法也存在了能量的缺额,但相较于MILP方法所出现的能量缺额更小.基于上述分析,本文方法能够在用能在各个场景的用能高峰期,相较于传统的MILP规划方法,能够更好的应对系统中的N-1故障,保证系统的安全稳定运行.此外,对于表中出现能量的富余状情况,表明系统有能力应对由于设备N-1导致的能量缺额,在实际运行过程中,可通过调度的干预,使得系统达到能量的实时平衡,不会导致能源的浪费.

5 结论

针对综合能源系统的配置优化问题,本文提出一种考虑系统源-网-荷多元不确定性的配置规划方法.该方法考虑可再生能源出力与用户负荷预测的不确定性、设备N-1运行不确定性,建立了基于多目标-机会约束规划的双层规划模型.对于多目标优化获得的帕累托解集,采用信息熵与逼近理想排序法相结合的综合评价方法,实现对各备选方案的综合评价以确定最终的设计方案.实验部分将本文方法应用于国内某区域综合能源系统的最优配置设计,在给出最优的配置方案的同时,也设计了考虑多元不确定性的典型场景的设备运行策略.通过设计对比实验,验证了本文所提优化模型与优化方法的有效性.然而,本文方法在衡量光伏出力与负荷预测结构不确定性时,均采用正态分布其进行建模,在今后的研究中,可考虑采用基于数据的辨识方法以获得更准确的不确定性模型.