奇异值分解下在线鲁棒正则化随机网络

于 洋,邓 瑞,余 刚,庞新富

(1.沈阳航空航天大学自动化学院,辽宁沈阳 110000;2.矿冶过程自动控制技术国家重点实验室,北京 100160;3.矿冶自动控制技术北京市重点实验室,北京 100160;4.沈阳工程学院自动化学院,辽宁沈阳 110000)

1 引言

在复杂的工业过程中,为了实现运行指标的闭环优化控制,通常需要采用建模法[1]对运行指标进行准确测量.建模方法的研究主要分为两个方面: 机理分析建模方法和数据驱动建模方法[2].传统的机理分析建模方法在城市电网电流耦合、医学图像诊断、极端天气的预测以及飞行控制[3-6]等领域有重要的研究.但是,机理分析的建模方法因难以获取系统的基础知识和关键参数,会导致一定的偏差[7].数据驱动的建模方法利用输入输出数据来建立对运行指标的估算模型,因此被广泛地用于解决高频电能转换、多机场系统运行、背景图像更新以及核反应堆中热流体现象等实际问题[8-12].

目前,人工神经网络[13]是最重要的数据驱动建模方法之一.神经网络可以通过学习大量的训练数据来拟合复杂非线性函数[14],它具有处理复杂系统的自学习能力,可帮助解决增值评价中有关模型构建、数据处理及大规模应用的问题[15].按照隐含层的层数,可以将其划分为多层前向型和单层前向型神经网络.多层前向型神经网络,拥有优良的逼近和泛化能力,被广泛研究和应用;单隐含层前向神经网络(singlehidden layer feed-forward neural networks,SLFN)[16]

亦具有较好的逼近性,反向传播神经网络(back propagation,BP)算法是主要的SLFN权值调整算法,已被用于补偿光纤陀螺温度、监测土地荒漠化趋势、人体动作识别以及网络安全评估[17-20]等.然而,BP算法在学习过程中效率较低,限制了SLFN的发展与应用[21].

随机权神经网络[22](random vector functional link network,RVFLN)解决了BP 算法学习效率低的问题.RVFLN的输入和输出是由一条直线链直接相连的,且输出层同时连接输入层和增强节点并汇集了SLFN网络的优点.由于RVFLN简单的训练过程以及万能逼近特性[23],在实际工业过程中得到广泛的应用.

近年来,为了提高RVFLN 的性能,学者们已提出许多改进策略.在权值变换方面,文献[24]将RVFLN的随机权重控制在[0,1]之内,建立了小范围RVFLN,提高了算法的泛化性能.文献[25]将合适的带权重因子的特征向量作为输入,提出了将经验小波变换与希尔伯特变换结合的加权RVFLN,可以准确预测故障位置.在此基础上,针对深度结构的神经网络大而时变的特性,文献[26]将经验小波变换和鲁棒最小方差RVFLN法相结合,以提高预测精度.文献[27]提出了鲁棒多核RVFLN,用于计算高度非平稳单的组合电能质量事件,以获得突出的识别精度和稳健的抗噪性能.另外,为减少隐藏节点的数量,文献[28]利用增量学习的方法,使部分隐藏节点不被随机选择,提出了选择性集成深部双向RVFLN.同时,由于工业生产往往具有慢时变特性,所建立的数据模型的参数也应随之改变.因此,文献[29]提出了自适应半监督的RVFLN,对模型参数进行了优化,并且其学习速度和精度均优于传统方法.文献[30]提出了在线鲁棒随机权神经网络(online robust RVFLN,OR-RVFLN)算法,该算法可以有效地减少内存,加快运算效率,并且具有良好的鲁棒性能.

目前,这些算法仍属于批处理最小二乘算法,输出权值矩阵的估计可能存在不适定问题,会导致计算误差偏大,从而影响预测精度;并且由于较小奇异值的存在,隐含层输出矩阵接近于奇异矩阵,从而影响模型的输出精度.因此,针对该问题,本文提出了基于奇异值分解的在线鲁棒正则化随机权神经网络(singular value decomposition online robust regularization RVFLN,SVD-OR-RRVFLN).

首先,该算法在OR-RVFLN的权值估计中引入带有惩罚项的损失函数,得到在线鲁棒正则化RVFLN(OR-RRVFLN),并且,对每一个隐含层输出矩阵进行奇异值分解,从而得到所提的SVD-OR-RRVFLN 算法.其次,本文对所提算法进行必要性和收敛性的证明.最后,基于Benchmark数据集和实际的磨矿粒度数据对所提算法进行实验分析,证实该算法在提高了模型的预测精度的同时保持了更高的鲁棒性能.

2 相关算法

本节主要介绍在线鲁棒随机权神经网络和奇异值分解算法,以此来引出本文所提的基于奇异值分解的在线鲁棒正则化随机权神经网络.

2.1 在线鲁棒随机权神经网络

当N组数据样本(xi,yi)采样时,存在L个隐含层节点的SLFN的成本函数可以用误差平方和公式表示,即

其中:vj是输入权值向量;bj是隐含层第j个节点阈值;ωj是第j个隐含层节点和输出层节点相连的权重.不同于SLFN需要调节所有参数,RVFLN可随机选取vj和bj,只需求权重ωj,就可保证网络的逼近能力.因此,式(1)可转化为线性二次优化问题,即

式(2)的矩阵形式表示为

其中:H=[h(x1)···h(xN)]T∈RN×L为隐含层输出矩阵;h(xN)=[φ(v1,b1,xN)···φ(vL,bL,xN)]为隐含层的特征映射;N为样本数;W=[ω1ω2···ωL]T∈RL为输出权值向量;Y=[y1y2···yN]T∈RN为实际的被测向量.利用方程HW=Y,可以得到输出层的权重估计值,即

式中H+=(HTH)-1HT为H的摩尔广义逆[31],将其代入到式(4)中,就得到了最小二乘解,即

在RVFLN的权值估计中引入加权最小二乘[32],可提高RVFLN的鲁棒性,即

权值W的估计如下:

其中P=diag{p1,p2,···,pN}为惩罚权重矩阵,可根据样本数据的可靠性进行调整,采用核密度估计(kernel density estimation,KDE)方法[33]进行估计.

为了减小存储空间和提高运算速度,在线鲁棒RVFLN[23]受到关注,具体算法如下: 分别定义初始输出权值和设置初始权重矩阵为P0,即

根据式(7)和式(9)的解,可以写为

根据反演公式(A+BCD)-1=A-1-A-1B(C-1+DA-1B)-1DA-1,可得

把式(12)代入式(10)中,可得

综上所述,当第k个数据块产生时,网络参数的权值更新算法如下:

2.2 奇异值分解算法

随着大数据技术的飞速发展,矩阵分解特别是矩阵的奇异值分解(singular value decomposition,SVD)在数据检索、图像压缩、人脸识别和故障诊断等领域有着广泛应用[34-35].如今已经衍生出许多SVD的变体,包括随机SVD[36]、顺序截断高阶SVD[37]、改进SVD[38]、Tikhonov 正则化改进随机截断SVD[39]、局部均值分解SVD[40].

假设存在一矩阵A ∈Rm×n,使得

其中:U=[u1u2···un]∈Rm×n是m×n阶酉矩阵;D=[d1d2···dn]∈Rn×n是n×n阶对角矩阵;Σ=diag{σ1,σ2,···,σn}∈Rn×n是n×n阶酉矩阵;ui是第i个正交向量;di是第i个奇异值;m和n分别是矩阵A的行和列.

通过奇异值分解,可以去除矩阵中存在的极小的奇异值,从而提高矩阵的输出精度.

3 基于奇异值分解的在线鲁棒正则化随机权神经网络

通过第2节对相关算法的说明,本节主要介绍了所提算法的具体形式,描述了算法的具体步骤,并且对算法的必要性和收敛性进行了分析.

3.1 SVD-OR-RRVFLN算法具体形式

隐含层输出矩阵H求摩尔广义逆H+的过程可能会产生矩阵的不适定问题,为此,本文将l2正则化引入到式(7)中,得到

其中µ为正则化参数.

根据式(8)-(14)(17),得到OR-RRVFLN递推公式,即

奇异值分解法可以提高隐含层输出矩阵的精度.因此,本文对式(18a)-(18c)中每一个隐含层输出矩阵H进行奇异值分解,其表达式为

式(18a)-(18d)-(19)构成了本文所提的SVD-ORRRVFLN算法.在式(18d)中引入了正则化项,解决了由逆矩阵引起的不适定性;同时,根据式(19),奇异值分解算法去除了隐含层矩阵分解后产生的极小的奇异值,进一步提高了模型输出的精度.

3.2 SVD-OR-RRVFLN算法描述

SVD-OR-RRVFLN算法包括离线和在线两个学习过程,具体学习过程如下：

步骤1离线学习阶段.

1)选取隐含层节点数L,随机分配输入权重vj和bj;

2)从数据中选择M组训练样本(M/5>L),采用5折交叉验证法,分别进行5次实验,每次选择其中一组作为测试样本,其余为训练样本;

4)计算5次实验估计误差的均值,判断是否具有最小的误差均值,满足则给出和,然后,进入在线学习阶段;不满足则继续选取其他L,重新进行验证试验.

步骤2在线学习阶段.

1)选取最大迭代次数Kmax,令k=1;

2)当新的数据产生时,根据式(19)求分解后的隐含层输出矩阵Hk;

4)如果k=Kmax,结束;否则,令k ←k+1,返回2).

3.3 SVD-OR-RRVFLN算法必要性的证明

定理1设ΔY和ΔW分别代表Y和W的偏差,可满足如下不等式:

其中E(H)=‖H‖‖H-1‖为条件数.

证根据公式

所以,由式(22)可得

根据范数的相容性[41],式(21)(24)的表达如下:

用式(26)除以式(25),可以得到如下不等式:

假设隐含层输出矩阵H特征值的最大值和最小值分别为σmax和σmin,根据文献[42],有如下关系式:

根据式(29)可知,当奇异值接近于0时,条件数变得非常大,矩阵接近于奇异矩阵,影响计算精度,导致最小二乘方法不容易对普通的函数进行拟合,并且限制了RVFLN神经网络的学习能力.因此,本文将正则化参数和奇异值分解方法引入到OR-RVFLN中.

3.4 SVD-OR-RRVFLN算法收敛性的证明

定理2设ε=Y-HW是零均值的白噪声,则式(18a)给出的是一致收敛的,即

其中α是模型参数真值.

根据式(18a)(32),可得

设矩阵Ak的特征值是η,则下式成立:

式中x是非零特征向量.把式(33)代入到式(35)中,可得

根据式(19),进一步有

4 性能评估

为了验证算法的有效性,本文将所提的SVD-ORRRVFLN,OR-RVFLN[30]和OR-RRVFLN[43]算法进行比较.OR-RVFLN 算法[43]中逆矩阵的求解采用MATLAB提供的pinv(·)函数来实现,神经网络隐含层的节点数采用交叉验证法进行确定.

本实验先把输入和输出的数据归一化到区间[0,1]上;再将不同的算法分别独立运行50次;最后,通过选取测试数据的均方根误差(root mean square error,RMSE)、标准差(standard deviation,Dev.)以 及平均相对误差3种性能指标,验证算法的预测精度和鲁棒性能.

4.1 Benchmark数据集

本实验采用加利福尼亚大学欧文分校所提供的Benchmark数据集验证所提算法性能1http://archive.ics.uci.edu/ml/machine-learning-databases/,Benchmark数据集属性如表1所示.

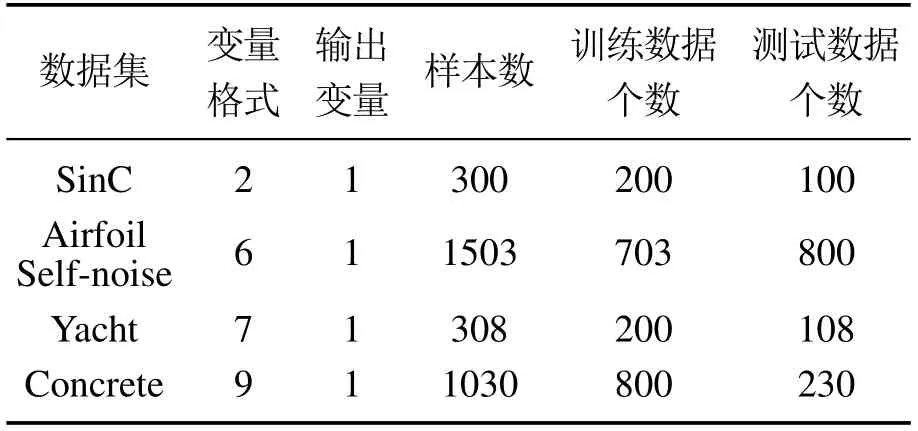
表1 Benchmark数据集属性[30]Table 1 Benchmark datasets attributes[30]

4.2 比较实验

对于每一个数据集,首先在固定的范围内,即0.01,0.1,0.5,1,2,3,4,5,6,7,8,9,10,选取正则化参数,所提算法在数据集上对不同正则化参数的估计结果如表2所示.通过表2发现,当正则化参数分别为3,5,8和0.5时,所对应的均方根误差和标准差最小.

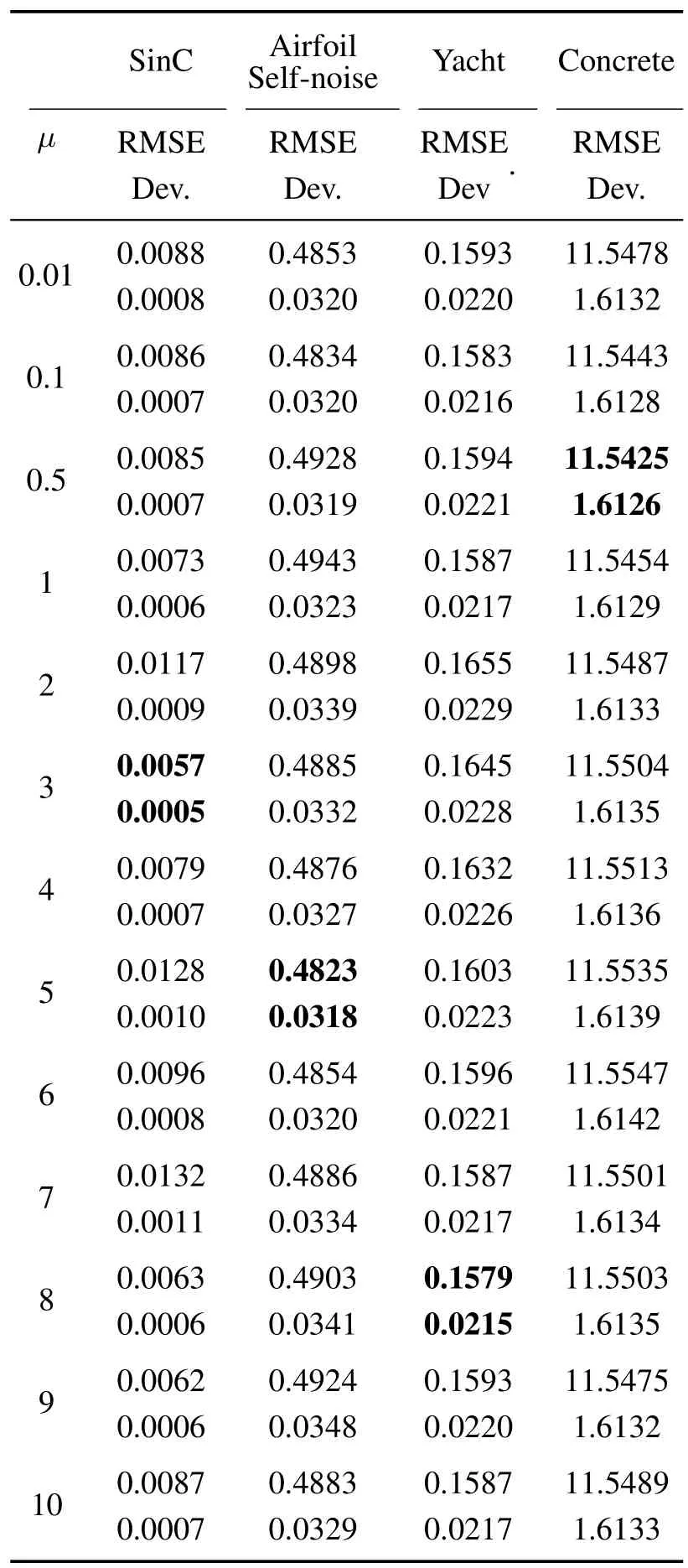
表2 不同正则化参数的估计结果Table 2 Estimation results of different regularization parameters

选取的最优正则化参数用于所提算法和OR-RR VFLN算法[43],并且与OR-RVFLN算法[30]进行比较,其结果如表3所示,对于每一个数据集,所提算法可获得最小的均方根误差和标准差,OR-RRVFLN[43]次之,OR-RVFLN[30]最大,实验结果证实了所提算法具有较高的鲁棒性能.同时,为了便于观察所提算法在预测性能上的优势,本文以SinC数据集为例加以说明.从图1可以看出,相比于另外两种算法,SVD-OR-RRVFLN算法的输出值更加接近真实值;根据相对误差图(图1)和平均相对误差表(表4)可知,与另外两种算法相比,本文所提算法的相对误差以及平均相对误差都是最小的.因此,实验验证了所提算法具有较高的预测性能.

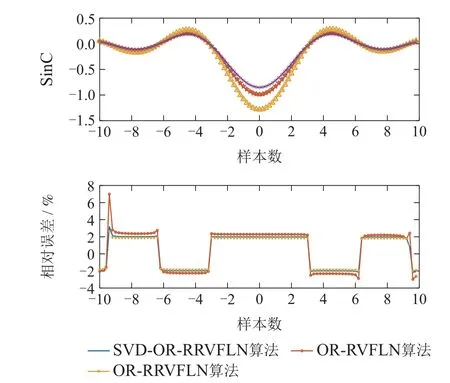
图1 3种算法在SinC上的估计结果和相对误差Fig.1 Estimation results and relative error of three algorithms on SinC

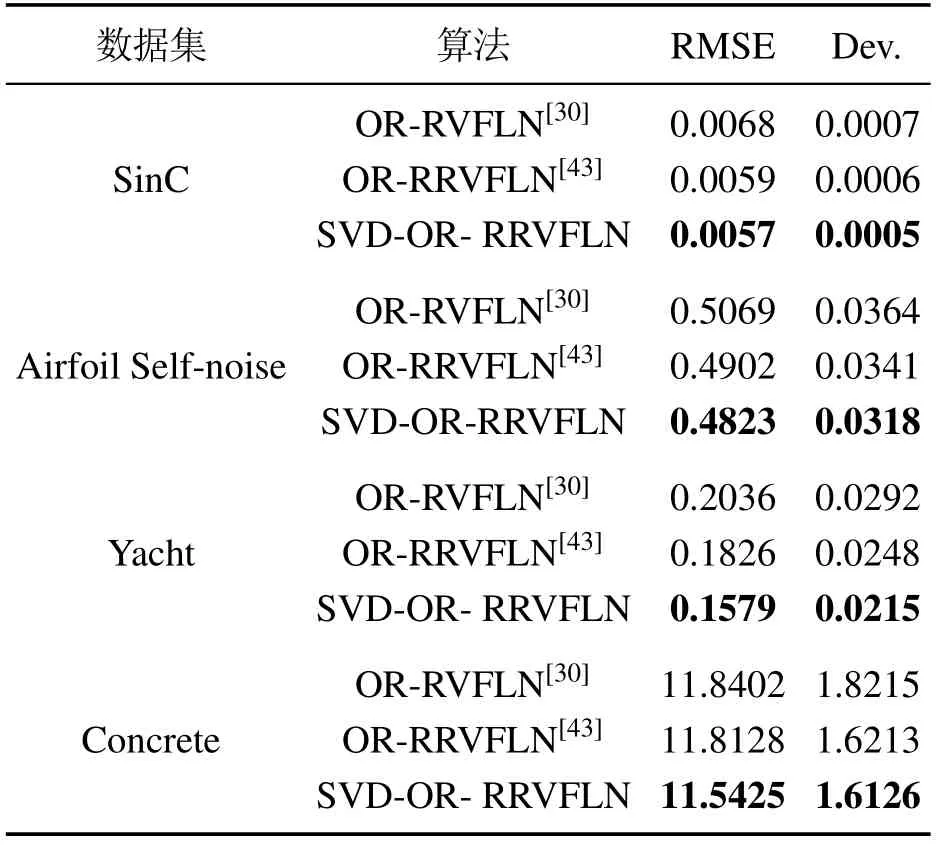
表3 3种算法在Benchmark数据集上的比较Table 3 Comparison of three algorithms on Benchmark datasets

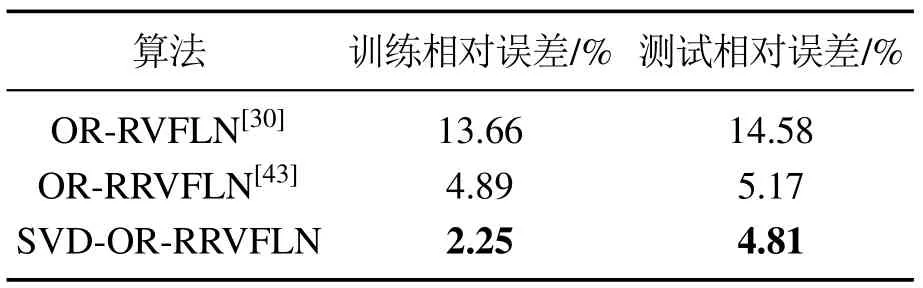
表4 3种算法在SinC上的平均相对误差比较Table 4 Comparison of average relative error of three algorithms on SinC

上述实验说明了,在Benchmark数据集上,所提的SVD-OR-RRVFLN算法不仅具有较高的鲁棒性,在预测精度方面具有明显的优势.

4.3 SVD-OR-RRVFLN算法在磨矿过程指标预测中的应用

赤铁矿一段磨矿过程的工艺流程如图2所示.该过程中原矿先经过传送带送入球磨机进行研磨,再通过钢球不断破碎,生产出一定浓度的矿浆.同时,向磨机中加入一定量的水,以将矿浆浓度调节在限制范围内.粉碎后得到的浆液将被连续地进入到螺旋分级机内进行分级,并且把一定量浓度的研磨水直接添加到螺旋分级机腔中,以便随时调节其浓度;把检验不合格的矿浆再送入球磨机中继续研磨,而从分级机溢流出的标准矿则送入选别工艺.

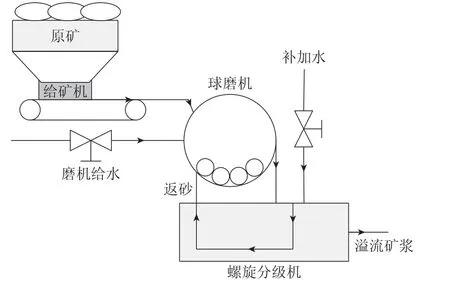
图2 赤铁矿一段磨矿过程的工艺流程Fig.2 Process flow of primary grinding process of hematite

由于赤铁矿矿石性质不稳定且矿石颗粒具有磁团聚现象,实验室化验方法无法满足磨矿粒度闭环优化控制的要求.传统的模型驱动的建模方法会因为一些条件的忽略而引起较大的误差[30].数据驱动建模方法是一种黑箱建模方法,可有效地提高模型的精度和鲁棒性.本文采用70 组测试数据,将所提的SVD-ORRRVFLN算法应用于磨矿粒度软测量模型的建模中,以此来验证所提算法性能.

表5为所提算法对不同正则化参数的误差结果.在表5中选取使RMSE和Dev.值最小的正则化参数;图3是3种算法下磨矿粒度估计的预测结果.为进一步分析3种算法的性能,分别计算不同算法的结果以及相对误差,并在表6和图4中给出.从图4可以看出,除了在样本数30～40区间内,所提算法总体上具有最小的相对误差;同时根据表6,进一步验证了所提算法具有最小的均方根误差,标准差,以及平均相对误差,说明了SVD-OR-RRVFLN算法在磨矿过程数据中整体上具有良好的预测精度和鲁棒性能.

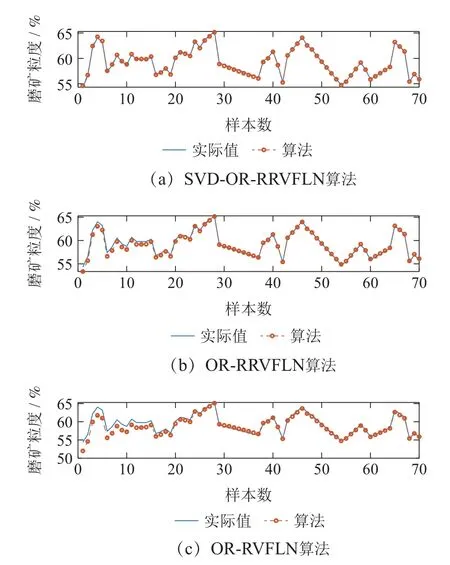
图3 3种算法在磨矿粒度上的估计预测结果Fig.3 Estimation prediction results of three algorithms on grinding particle size

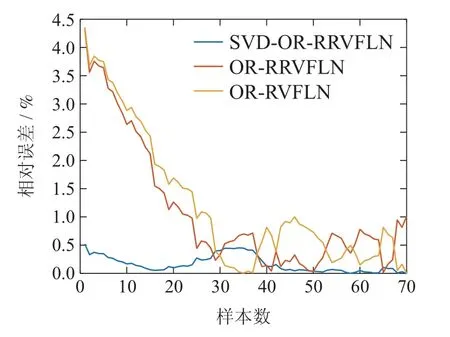
图4 3种算法在磨矿粒度上的相对误差Fig.4 Relative error of three algorithms on grinding particle size

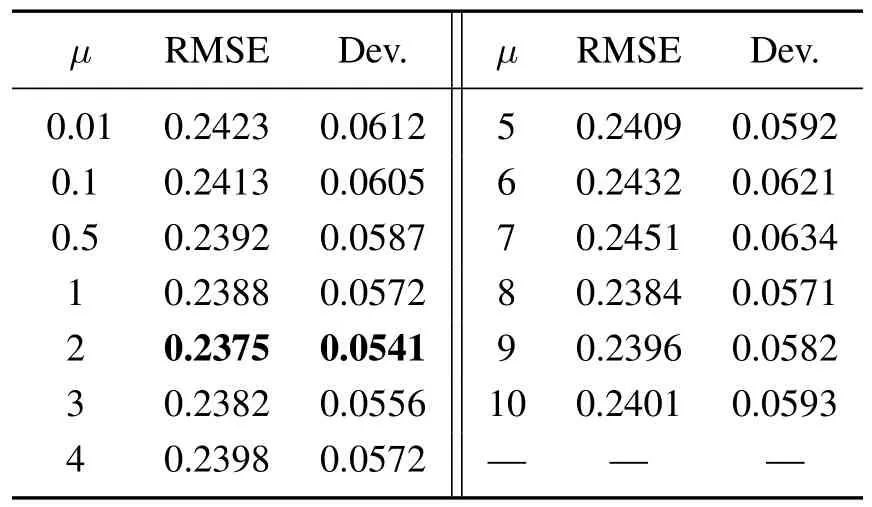
表5 不同正则化参数的误差结果Table 5 The error results of the different regularization parameters

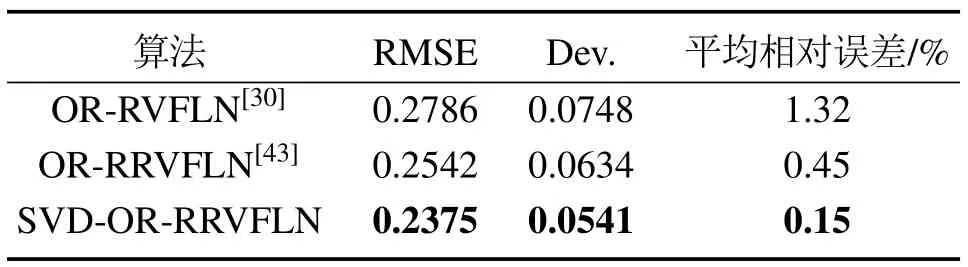
表6 3种算法在磨矿粒度上的估计误差结果Table 6 Estimation error results of three algorithms on the grinding particle size

为了验证所提算法的时效性,本文对比了所提算法与另外两种算法接收新样本时的在线训练时间.比较结果如图5 所示,所提方法的平均训练时间为0.008 s;OR-RVFLN[30]算法的平均训练时间为0.02 s,OR-RRVFLN[43]算法的平均训练时间为0.015 s.伴随着样本的累积,所提算法的训练时间相对于另外两种算法更加稳定.通过以上的实验对比发现,所提算法不仅有较高的鲁棒性能和预测性能,而且有更少的时间消耗.因此,所提的SVD-OR-RRVFLN算法提高了训练速度.

图5 在线训练时间Fig.5 Online training time

5 结论

本文针对逆矩阵的不适定问题提出了奇异值分解的在线鲁棒正则化随机权神经网络,即SVD-OR-RRVFLN方法.将正则项添加到输出权值的估计矩阵中,并采用奇异值分解法对整个网络的隐含层输出矩阵进行更新,从而提高了模型的预测精度.同时采用核密度估计法,对整个SVD-OR-RRVFLN网络的权值矩阵进行更新,以提高算法的鲁棒性能.基于Benchmark数据集的仿真实验表明: 与其他方法相比,本文所提的方法能有效提高预测精度和鲁棒性能.同时,这个方法应用于磨矿过程中,进一步说明所提算法不仅可以提高模型的预测精度和鲁棒性能,而且加快了训练速度.