集成数据挖掘知识的可解释最优超球体支持向量机
陆思洁,范 頔,渐 令,郜传厚†
(1.浙江大学数学科学学院,浙江杭州 310027;2.中国石油大学(华东)经济管理学院,山东青岛 266580)
1 引言
传统的黑箱建模方法,如支持向量机(support vector machine,SVM)、神经网络等,由于不涉及被研究对象的内部结构和作用机制,而仅利用其输入输出关系即可从整体上把握其行为,因此受到广泛关注并常被用来处理一些复杂系统,如人脑[1]、黑洞[2]、工业过程[3]等.可以说,黑箱建模提供了一种认识复杂对象的有效途径.但近年其发展也受到诸多挑战,其中最重要的一条是黑箱模型的运行方式缺乏可解释性及透明性,不能把模型结果直接转换为能被理解的知识;同时,也不能利用问题本身具有的先验知识改进模型性能,因此,模型结果的说服力和对问题的实际指导价值都减弱,这在很大程度上限制了黑箱模型更为广泛、深入的应用.为此,研究黑箱模型的可解释性就变得十分重要[4-7],特别是在需要对作出的决定给出明确解释的领域,如信用风险分析、医疗诊断等.
黑箱模型的可解释性在数学上并没有严格、统一的定义,通常理解为人们对决策的理解程度或对模型结果的预知程度.因此,增强黑箱模型的可解释性有以下两个途径: 1)从黑箱模型的输出端提取规则,将系统中隐含的知识以一种易于理解的方式表达出来[8-12];2)在黑箱模型的输入端集成先验知识[13-17].其中先验知识是指目标系统建模前就已知的任何相关信息(包括领域知识、专家经验、数据等),并且在有限数据条件下,加入先验知识是提高黑箱模型泛化性能的唯一手段[18].本文主要关注第2种方式,即在黑箱模型的输入端集成先验知识以增强其可解释性.
先验知识的种类繁多,其集成黑箱模型的方式也因此而不同.以SVM黑箱建模技术为例,其先验知识的集成方法可分为3类: 1)结构改进.该方法主要通过合理地设计核函数的形式来实现先验知识集成,如引入变换不变性构造新核函数[19]、定义新的距离代替欧氏距离构造新核函数[20]、利用Haar积分构造新核函数[21]以及利用先验知识直接构造核函数[22-23]等;2)算法改进.该方法通过SVM本身算法的设计来集成先验知识,如通过在SVM优化问题中增加相应的线性或非线性不等式约束来实现线性或非线性先验知识的集成[24-25]、利用半定规划算法实现变换不变性先验知识的集成[26]等;3)数据样本.该方法主要通过对样本数量或样本重要程度的控制来集成先验知识,如利用先验知识产生更多训练样本的虚拟样本法[27]、通过设置正则化权重系数融合样本分布不平衡[28]、样本准确度[29]和引入新的数据集Universum[30-31]等先验知识的权重约束法.
从数据中挖掘先验知识并进一步集成至黑箱模型已展现出较好的透明化效果.笔者之前的工作[32-33]实现了从数据中挖掘二维线性先验知识,并以线性不等式约束的形式集成至软间隔SVM模型.通过将集成知识后的模型改造成标准的二次规划问题,得到了部分可解释的软间隔支持向量机模型,并在一些公共样本集和实际高炉数据集上展现了可解释性增强效果.但因挖掘的知识为线性先验知识,且在形成不等式约束时仍仅利用产生知识的数据点(即本已存在的数据点),对于构造的模型并没有增加新的数据信息,导致透明化后的模型精度提升并不明显.特别是对比例偏低的不平衡样本点,新模型几乎没有效果;并且,模型的评价指标仅采用预测精度,未能合理体现处理不平衡数据集的模型的真实性能.为此,本文以最小体积最大间隔支持向量机(small sphere and large margin,SSLM,下文称为最优超球体支持向量机)[34]为基准模型(其工作原理是通过构建超球体执行分类任务,并且常用来处理不平衡数据集),开发从数据中挖掘非线性圆形知识的算法.为更好的处理数据的不平衡性,进一步开发圆形知识所包含区域的数据点离散化算法,使得知识所约束的数据点不仅包含产生知识的原有数据点,还产生新的数据点.最后,将挖掘的非线性圆形知识集成到SSLM黑箱模型,构建可解释的最优超球体支持向量机模型,记为i-SSLM.这里模型的效果通过12组数据集(包括10组公共样本集和2组实际高炉数据集)以及选择对比传统的4种模型C-SVM[35],支持向量数据描述(support vector data descriptio,SVDD)[36],SSLM[34]和最大间隔双球支持向量机(maximum margin of twin spheres support vector machine,MMTSSVM)[37]加以展示.相比较于这些黑箱模型,i-SSLM模型本身具有能有效处理不平衡数据的优势;其次,它通过融入非线性先验知识可对输出结果进行解释;最后,它通过离散化知识所框区域,增加新的样本信息,有望提高模型的分类性能.
论文的结构如下: 第2节介绍了SSLM模型的工作原理及逻辑知识如何转化为不等式;第3节给出一种从数据中挖掘圆形先验知识的算法并将挖掘的知识以不等式约束的形式集成至SSLM模型,构造具有可解释性的i-SSLM模型;第4节通过10个公共样本集和2个高炉实际样本集验证i-SSLM模型的有效性,并与传统的C-SVM,SVDD,SSLM,MMSSVM这4种模型进行对比;第5节总结全文并对将来工作进行展望.
符号说明:文中小写粗体字母a表示列向量,大写粗体字母A表示矩阵,上标AT表示矩阵A的转置;Rm表示m维实数空间,表示m维正实数空间;对任意x ∈Rm,‖x‖表示2-范数,
2 预备知识
本节将简单介绍最优超球体支持向量机的工作原理和逻辑知识的表达及转换.
2.1 最优超球体支持向量机
最优超球体支持向量机(SSLM)常用来处理不平衡数据集的分类问题,针对数据集(假设xi∈Rm,yi∈{+1,-1},数据集中正类样本个数n+远大于负类样本个数n-),其工作原理是通过构建一个尽可能多地包围正类样本点的超球来完成分类任务.若样本点落在超球内,则标识为正类;若样本点落在超球外,则标识为负类.同时,为了实现最大程度的分离,要求球面到负类样本点的距离应尽可能大.数学上,SSLM[34]可表示为
其中:R和c分别为超球的半径和球心;ρ ∈R,ρ2≥0表示超球表面与负类点的间隔;分别为正类样本点和负类样本点;ϕ:Rm →F是一个从Rm到无穷维空间F的高维映射;ξi和ηj为松弛变量;ν,ν1,ν2是3个正常数.
通过引入拉格朗日乘子α=[α1α2···αn]T并进行对偶变换,可求解得模型(1)的决策函数为
其中K(x,x)=〈ϕ(x),ϕ(x)〉为核函数.当f(x)≥0,则y=+1;当f(x)<0,则y=-1.
2.2 知识的表达及转换
知识的定义有许多种,而关于对象的逻辑推理式是其中一种重要的表现形式.以上述二分类问题为例,则其逻辑知识可以表达为
式中:g:Γ →Rk是定义在Γ上的k维函数,Γ ⊆Rm;X+表示正类样本集合.该式的物理意义是集合{x|g(x)≤0}中所有点都属于正类,类似可表达负类逻辑知识.注意这种以逻辑形式给出的知识并不能直接融入SSLM模型,需将其转化为方便集成的模式.
数学上,式(3)中的逻辑表达式与下述方程组等价[38]:
进一步,他们证明了若式(3)或式(4)成立,则存在u∈,使得
显然,式(5)可作为约束直接集成到SSLM模型中.
3 可解释的最优超球体支持向量机
在第3节中,将开发算法从数据中挖掘圆形非线性知识,并将其集成到SSLM模型中以获取可解释性.
3.1 数据型非线性知识挖掘算法
从数据中挖掘知识,关键是给出式(5)中g(x)的具体表达式,这在特征维数较高、函数关系较为复杂时通常十分困难.Chen等人[32-33]提出一种基于数据的双变量的线性先验知识挖掘方法,通过将特征空间投影到二维空间,并在所有二维特征空间中挑选能最大分离正类(或负类)样本的线性先验知识;同时挖掘的线性先验知识以不等式约束的形式集成到黑箱SVM模型中,创建一个能同步优化挖掘知识的正确性和黑箱模型的优化问题.受Chen等[32-33]启发,本文只考虑由系统两个特征变量所生成的知识,即g:Γ ⊆R2→R,意味着把样本点从输入空间Rm映射到一个二维子空间,用X(i)OX(j)(i,j=1,···,m) 来表示.同时,考虑到SSLM的工作特点(构造最优超球体进行分类)和样本非平衡性(正类样本远多于负类样本),本文寻找二维平面X(i)OX(j)上的圆形正类知识,即
式中: (tanθ1,tanθ2)为圆心,r为圆半径.这里圆心的设置是通过正切函数实现,θ1和θ2在区间中均匀选取10个点进行交叉组合设置.具体算法如算法1(见表1)所示.

表1 算法1: 数据挖掘圆形非线性知识Table 1 Algorithm 1: Circular nonlinear knowl-edge mined from data
步骤7的优化问题保证正类样本点尽可能多的在圆内,约束表示所有的负类样本点都要在圆外,即在二维子空间中,正类样本点尽可能多的分类正确,而负类样本点全部分类正确.实际求解时,每次循环均固定两个特征xi与xj及θ1和θ2的取值,在约束条件成立情况下,计算目标函数值,即正类样本点分类正确的个数,循环结束时目标函数最大值即为所求.在最后的输出结果中,除了得到圆形知识之外,圆内所包含的正类样本点也同时得到.
注1算法1挖掘的知识将以约束的形式集成到SSLM模型,因其能确保模型在圆内的正类样本点分类正确,即I1内的样本点,所以集成这类知识后的SSLM具有一定的可解释性.同时,模型的精度也有望提高,因此确保了一部分样本分类正确.
例1本文将算法1应用于UCI数据库里的Liver Disorders数据集1https://archive-beta.ics.uci.edu/ml/datasets/liver+disorders.该数据集共含有6个特征变量,345个样本点,其中正类样本点200个,负类样本点145个.为构建不平衡数据集,本文随机选取70%的正类点,即140个正类点,和16个负类点,使得正类点与负类点比例大约为9:1.应用算法1,最后可得在X(2)OX(3)二维子空间,圆内所包含的正类点个数最多,为45个正类点.因此,选择
用于后面表达该数据集挖掘的非线性知识.
注2 式(7)的知识是由140个正类样本点所生成,但在圆形知识形成后,由式(5)知,圆形图所包含的整个区域都属于正类知识,将其直接集成至SSLM模型将会得到一个半无穷规划问题,难以求解.为了尽可能利用区域知识,同时也为了方便集成SSLM模型,本文对区域里的知识离散化来获取更多的正类样本点,算法2(见表2)即为实现这一目的而开发,其主要思想是将I1中的l个点作为网格点形成网格,并在圆形区域内随机选取除I1以外的其它2l个网格交点作为虚拟正类样本点,最终的知识点集合为I=I1∪I2.当然,这些新增加的样本信息作为约束将会增加模型的复杂度,进而可能对模型训练不利,笔者后面将通过引入松弛因子来强化它们的正确性.

表2 算法2: 圆形知识离散化Table 2 Algorithm 2: Discretization of circular knowledge
基于式(3)-(5),离散化后的圆形知识可以表示为
3.2 圆形知识集成的最优超球体支持向量机
将形如式(8)的知识集成到SSLM模型可得
其中:δ与ν,ν1,ν2意义相同,表权重参数;zp为松弛变量,测量圆形知识的偏差;平面上的投影分量.为区别SSLM,称模型(9)为可解释的最优超球体支持向量机,记为i-SSLM.
通过引入拉格朗日乘子并做对偶变换,再进一步利用KKT(Karush-Kuhn-Tucker)条件,可得i-SSLM的决策函数为
注3 本质上,i-SSLM模型(9)是通过集成先验知识和增加训练样本来增强黑箱SSLM模型的可解释性,但这并不是对现有知识集成[32-33]及产生虚拟样本方法[27]的组合.i-SSLM 综合利用了SSLM模型能有效处理不平衡数据、集成的非线性圆形先验知识与SSLM模型类型相一致、增加的额外离散知识点提供了新信息等优势来提高分类性能.这里产生知识的方法以及增加离散样本点的方法都与上述文献不同,文献[32-33]产生的是线性先验知识,而文献[27]离散样本的方法是通过使用形态学运算符人为地细化和粗化线条来为每个示例生成两个额外的向量.
3.3 公共数据集实验
本文首先在10个公共数据集上进行实验,这些数据集均有相应的实际背景,它们的基本信息见表3,其中最后一列“Example size”是按照“#Example×#Feature”计算而得,用以衡量数据集的规模.对每个数据集,从正类样本中随机选取70%样本,同时从负类样本中按照正负比例约为9:1的数量随机选取样本构成训练集,剩下的正类、负类样本作为测试集.很显然,训练集具有不平衡性.按照i-SSLM 建模步骤,首先利用算法1在训练集上生成圆形非线性知识(区域),进一步利用算法2将圆形区域知识离散化并集成到i-SSLM模型形成式(9),最后通过训练集参数寻优和测试集验证可得模型的测试精度.
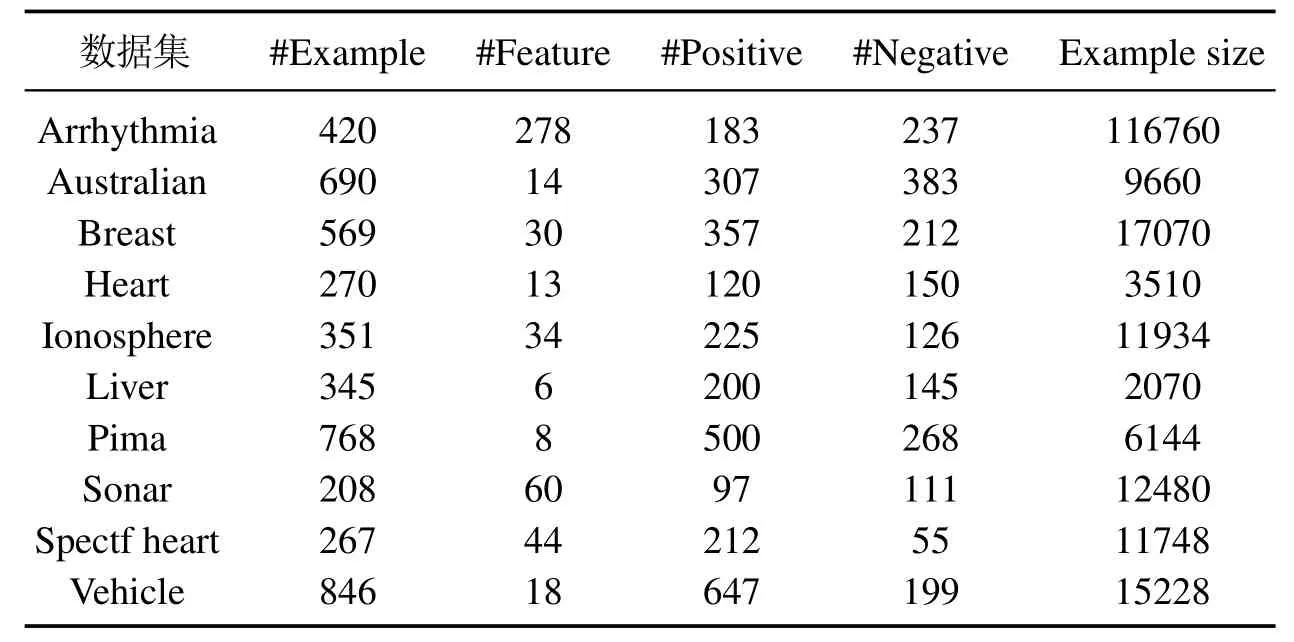
表3 10组公共数据集基本信息Table 3 10 sets of public dataset basic information
4 实验结果和讨论
本节将选用UCI数据库2https://archive-beta.ics.uci.edu/的10个公共数据集和2个高炉实际生产数据集为对象来验证本文所提方法的有效性.除了验证i-SSLM 模型外,本文还选取MMTSSVM 模型[37]、SSLM 模型[34]、经典的C-SVM 模型[35]和SSVD模型[36]进行对比实验.所有模型均选用高斯核为核函数,即
核参数以及模型中的其它参数采用网格搜索法确定.在C-SVM和SVDD模型中,包含2个参数: 惩罚参数C和高斯核参数σ;在SSLM模型和MMTSSVM模型中,均包含4个参数: 惩罚参数ν,ν1,ν2和核参数σ;而i-SSLM模型中包含5个参数: 惩罚参数ν,ν1,ν2,δ和核参数σ.为简化寻优,本文令SSLM,MMTSSVM和i-SSLM模型中的ν1=ν2,参数C的取值范围为{2-4,2-2,20,22,24}[34,37];模型SSLM和模型i-SSLM中参数ν和ν1的取值范围为{10,30,50,70,90}和{0.01,0.001}[34];模型MMTSSVM中参数ν和ν1的取值范围均为{0.1,0.3,0.5,0.7,0.9},参数δ的取值范围为{2-5,2-3,2-1},参数σ的取值范围为{2-4,2-2,20,22,24}[37].参数的寻优过程采用五折交叉验证法在训练集上实施,寻优结果用测试集进行测试.为了使结果更具说服力,本文用5次随机实验的平均结果作为评价标准,即每次实验随机产生训练集和测试集,得到最优参数和测试精度,共进行5次实验,取5次测试精度的平均值作为最终结果.所有实验都是在Python软件上进行,版本为Python 3.8,硬件配置为Intel(R)C ore(TM)i5-8250U CPU@1.60 GHz 1.80 GHz,RAM为8.00 GB.
式中: TP,FP表预测正确和错误的正类样本数;TN,FN表预测正确和错误的负类样本数.
表4给出了某次随机实验训练集上挖掘的各个数据集的圆形知识,表5报道了这些数据集5次随机实验的平均结果,其中G-means指标以“平均值±标准差”的形式给出,Time是训练时间的平均值.作为对比,本文在表5中同时给出了其他4种模型C-SVM,SVDD,SSLM 和MMTSSVM的对应结果.从表5可以看出,i-SSLM 在Arrhythmia,Australian,Liver,Pima,Sonar,Spectf Heart和Vehicle数据集上有更好的分类效果;而在Heart和Ionoshpere数据集上,MMTSSVM模型效果最好;在Breast数据集上,SSLM模型有最高的G-means值.表6统计了每种模型在所有数据集上的G-means综合排名.显然,i-SSLM具有最高的综合排名.但从表5的训练时间看,i-SSLM则没有优势,主要原因是因为知识的引入将会增加模型参数,从而导致训练时间变长.这里本文主要关心模型精度的提高,模型效率的改进将在以后的研究中进行关注.

表4 10组公共数据集的圆形非线性知识Table 4 Circular nonlinear knowledge of 10 sets of common datasets

表5 10组公共数据集实验结果Table 5 Experimental results from 10 sets of common datasets
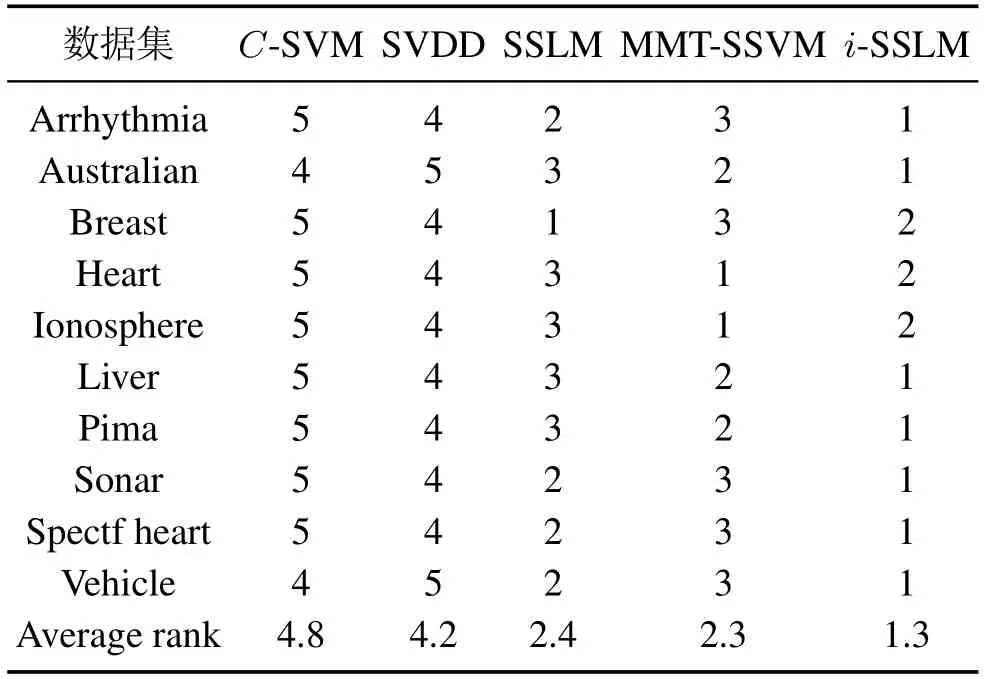
表6 5种模型在公共数据集上的综合排名Table 6 Comprehensive ranking of 5 models on public datasets
为了更好地从统计意义上对比这5个模型,本文引入Friedman检验对实验结果进行分析.在所有模型没有显著性区别的零假设下,计算可得=33.68 和FF=47.96,其中FF是服从(4,36)自由度的F分布.这一结果远高于F(4,36)在显著性水平α=0.05下的临界值2.63和在显著性水平α=0.01下的临界值3.89,表明这5 种模型具有显著性的差别.同时,根据表6可知,i-SSLM平均排名最小,因此,可以说明相较于另外4个算法,i-SSLM有更好的实验性能.
4.1 高炉数据集实验
高炉炼铁是钢铁生产工艺的上游工序,消耗整个工序近70%的输入能量,对其进行建模和控制一直都是钢铁生产过程中的重要课题.高炉炉温是评定生铁质量的关键指标,在实际中因其困难的测量问题,常常用高炉铁水含硅量作为炉温的指示剂[39]: 铁水含硅量的波动反映了炉温的波动,其持续上升和下降反映炉缸是向热还是向凉变化.因此,对高炉铁水含硅量的正确预测和控制构成了高炉操作指导的基础.针对这一重要问题,本文将用i-SSLM模型对高炉铁水含硅量进行分类预测.
本文选用与文献[40]中相同的高炉数据集,即从国内两座体积约为2500 m3和750 m3的高炉采集的数据,分别标识为高炉(a)和高炉(b).前者包含794个样本点,后者含有800个样本点,所涉及到的高炉变量个数分别为16个和7个,具体详见文献[40].因高炉是一个强惯性系统,本文同时考虑这些变量的延迟项对铁水含硅量的影响.文献[40]利用基于模糊熵的反向选择方法进行特征选择,即一个特征变量的模糊熵越大,表明这个变量越不重要.在特征选择过程中,高炉训练集首先被分成两部分: 训练集和验证集;然后,将所有特征变量输入SVM模型,通过训练、验证得到高炉(a)和高炉(b)的模型精度(即正确分类的数量与验证集大小的比率)分别为79%和69%;紧接着,按照模糊熵大小顺序依次挑选特征变量,如果删除一个变量可以使模型精度提高,则删除该变量,否则保留;最后,挑选出高炉(a)的特征变量,共42个,高炉(b)的特征变量共9个.由于这里选用的高炉、实验数据和文献[40]完全相同,本文直接选用他们的特征选择结果作为模型输入,输出的设置也沿用这篇文献的结果,即对高炉(a)/(b),硅含量在[0.41,1.13]/[0.37,2.20]视为正类,标识为+1;硅含量在[0.13,0.41)/[0.18,0.37)视为负类,标识为-1.因此,高炉(a)和高炉(b)可用的正负类样本数量分别为为679,115和584,216.
高炉实验与公共数据集实验设置有所不同,训练集和测试集通过下述5 种方式构造:从正类样本种随机选取70%样本,负类样本中分别随机选择10%~50%的样本构成训练集;剩下的样本作为测试集.对于每种模式构造的样本集,均进行5次实验,最终结果取5次测试结果的平均值;参数训练时仍采用5层交叉验证.为了更好地展现i-SSLM模型在高炉实验中的优势,本文同时对比了MMTSSVM模型.它们的参数寻优范围,除了i-SSLM模型的参数σ寻优范围为{20,22,24}外,其他和第3.3节公共数据集相同.
表7 展示了利用算法1在高炉(a)和高炉(b)中针对不同比例的负类样本点挖掘的非线性知识.以50%比例的负类样本点为例,图1展示了挖掘的圆形知识对样本的分类情况.从图中可以看出,所有的负类样本均在圆外,这意味着圆内所有样本点均为正类,包括数据集原有的部分正类样本点I1(三角形)及知识离散化产生的部分正类样本点I2(星形).这些样本在i-SSLM模型训练之前就已经明确需要分为正类,因此模型具有一定的可解释性.同时因为I2样本增加了新的数据信息,模型的精度也会随之提高.进一步观察表7所列知识(以高炉(a)为例),所涉及变量为x14(喷煤)和z(硅含量),这基本与高炉工艺原理较吻合.因为在高炉冶炼过程中,对硅含量的影响因素有很多,但其历史值(高炉强惯性特征)和喷煤量是两个非常重要的因素;同时,高炉是个滞后系统,喷煤量的调整作用会在一定时间之后显现出来.所以,本文所挖掘的知识和高炉实际知识是相对应的,这也反向说明了本文知识挖掘算法的有效性.
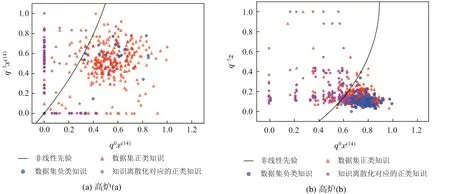
图1 高炉数据负类样本50%比例下挖掘知识的分类边界Fig.1 Mining the classification boundary of knowledge under the negative sample of blast furnace data is 50%ratio

表7 高炉数据挖掘的非线性知识Table 7 Nonlinear knowledge of blast furnace data mining
表8给出了i-SSLM 模型和MMTSSVM 模型在高炉数据集上的实验结果,包括G-means,Sen和Spe这3种指标的5次平均结果,同样以“平均值±标准差”的形式给出.由表8可知,对于高炉(a)数据集,i-SSLM比MMTSSVM有更高的G-means和特异度;当负类点比例为30%和40%时,i-SSLM的灵敏度略低于MMTSSVM.对于高炉(b)数据集,虽然i-SSLM的灵敏度和特异度在部分负类点比例上比MMTSSVM低,但是总体上,i-SSLM比MMTSSVM有更高的G-means.综合而言,在高炉数据集上i-SSLM比MMTSSVM展现了更好的性能.

表8 高炉数据的实验结果Table 8 Experimental results of blast furnace data
5 结论与展望
本文针对SSLM模型具有处理非平衡数据能力但缺乏可解释性等问题,提出从SSLM黑箱模型的输入端集成先验知识,以增强黑箱模型的可解释性和精度.论文取得的结果如下: 1)提出了一种从数据中挖掘2维圆形非线性知识的方法,圆内可最大限度地包含正类样本,而圆外则包含所有负类样本;2)开发了一种离散化圆形区域知识的算法,离散化后的数据点,不仅包含产生知识的原有数据样本点,还产生一些新的数据样本点;3)将挖掘的圆形先验知识以不等式约束的形式集成至SSLM模型,构造了i-SSLM模型,后者因确保圆内样本点为正类样本因而具有可解释性,又因离散化圆形知识增加了新的样本点因而同时具有更高的精度;4)10个公共样本集和2个实际高炉数据集例证了i-SSLM 模型在可解释性和精度上优于传统的C-SVM,SVDD,SSLM,MMTSSVM4种模型.
尽管i-SSLM模型展现了良好的性能,但仍有较大改进空间: a)挖掘的圆形知识只涉及两个特征变量,未来的研究可考虑涉及更多特征变量、更高维的球形或球体先验知识,以挖掘更准确的先验知识;b)挖掘的知识仅为判定样本为正类的先验知识,对于二分类问题,可进一步挖掘负类先验知识集成至黑箱模型,全面增强黑箱模型的可解释性;c)知识的引入使得i-SSLM模型包含更多的参数,导致后续的参数寻优和模型训练均耗费更长时间,如何提高i-SSLM模型的学习效率是未来研究的重点.

