面向高维多目标优化的双阶段双种群进化算法

曹嘉乐，杨 磊，田井林，李华德，李康顺

华南农业大学数学与信息学院，广州 510642

高维多目标优化问题在现实世界中广泛存在，如楼宇负荷优化调度[1]、汽车碰撞安全设计[2]和配送中心拣货系统作业[3]等。这类问题通常涉及三个或三个以上相互冲突的目标，提升其中一个目标的性能往往会导致其他目标的性能下降，因此需尽可能地优化这些冲突的目标使得总目标达到最优。近年来，进化算法作为一种启发式优化算法，因其能够模拟自然进化过程来解决各种复杂的优化问题而在多目标优化领域中得到了广泛应用。如今的高维多目标进化算法大致分为如下四类：

第一类为基于帕累托支配关系的高维多目标优化算法。这类算法一般基于两种策略来选择个体：第一种策略是通过改进帕累托支配关系来选择个体，该策略通常通过放宽帕累托支配关系，使得不可比较的解能够进行比较，从而增强环境选择压力。如CSDR-Dominance[4]、GPO-Dominance[5]等。这些算法虽然能提高高维多目标优化算法的选择压力，但是对参数依赖性很强，往往很难找到合适的参数。第二种策略则是通过新型的多样性选择标准来选择个体，如Zhou等人[6]采用一种基于全局和局部多样性的多样性维护机制来管理种群的多样性，Chen等人[7]通过多样性排序的方法来提高种群在不同类型帕累托前沿上的多样性。这些算法虽然在增加选择压力方面有效，但在平衡多样性和收敛性方面稍有不足。

基于指标的高维多目标进化算法属于第二类，如HyPE[8]、MaOEA-IGD[9]等。这些算法使用超体积（hypervolume，HV）[10]、反向世代距离（inverted generational distance，IGD）[11]等准确指标或估计的指标值来进行环境选择。然而，这些算法的计算成本是非常昂贵的，并且生成的解很难保证分布的均匀性。

第三类是采用新型自定义进化框架的高维多目标优化算法。如基于决策变量分类的DVC-MOEA[12]采用一种新型的决策变量分类方法来生成有前景的解，但是决策变量贡献的变化可能会导致错误的分类，从而影响算法效能。基于两阶段代理辅助进化算法TS-SAEA[13]通过将进化过程划分为收敛性阶段和多样性阶段，以分别提高种群的收敛性和多样性，但是对收敛性和多样性分别进行处理，可能无法保持收敛性与多样性的平衡。而Two_Arch2[14]则使用收敛性种群档案及多样性种群档案来指导种群的进化，该方法能够有效地维持收敛性和多样性的平衡，其缺点是在高维空间多样性档案难以更新，会导致解集的多样性变差。

第四类则为基于分解的高维多目标进化算法，该类算法通常采用均匀分布的权重向量将一个高维多目标优化问题分解成多个单目标子问题，然后同时对它们进行优化。其中，MOEA/D[15]、RVEA[16]是这类算法中的一些代表性算法。相较于其他三种类型的算法，该类算法具有计算复杂度低、能够提供良好的选择压力和维持多样性简单等优点。然而，当处理具有不规则形状的帕累托前沿时（例如断开、退化、反向、约束、严重缩放和复杂的帕累托前沿），使用预定义均匀分布的权重向量的算法性能会受到影响[17]，无法挑选出分布均匀的解，同时还会导致权重向量的浪费。

为了有效地处理具有不规则帕累托前沿的高维多目标优化问题，一种有效的方法是在进化过程中自适应地调整权重向量。例如，Liu等人[18]通过改进的k-均值聚类方法从种群中提取符合帕累托前沿形状的权重向量。Zhao 等人[19]采用双重调整策略对权重向量进行调整。Zhang 等人[20]周期性地将权重向量分组为多个子集，并将每个子集中的权重向量数量与边界个体形成的范围成比例，从而挑选出覆盖范围良好的解。

即使上述权重向量调整方法能够一定程度上处理具有不规则帕累托前沿的高维多目标优化问题，但是这些方法大多都只能处理具有不规则帕累托前沿的高维多目标优化问题，在具有规则帕累托前沿的高维多目标优化问题上表现较差。此外，在高维多目标优化问题中，保持种群的收敛性是相当具有挑战性的。而这些方法大多都是在预定义的权重向量的基础上进行权重向量的调整，需要多次对权重向量进行调整，虽然能够提高种群的多样性，但也会导致种群的收敛性变差。最后，这些方法在对权重向量调整时所需的参数较多，在不同的问题上使用固定的参数可能难以处理具有极端不规则帕累托前沿的高维多目标优化问题。

综上所述，在高维多目标优化问题上获得具有良好收敛性与多样性的种群是一项充满挑战性的任务，虽然基于分解的高维多目标优化算法在该问题上表现出色，但是其所生成的权重向量往往会与一些帕累托前沿的形状不匹配，从而无法有效兼顾处理具有规则和不规则帕累托前沿的高维多目标优化问题，最终导致算法的性能下降，甚至失效。

为了有效地处理具有规则和不规则帕累托前沿的高维多目标优化问题。本文提出了一种面向高维多目标优化的双阶段双种群进化算法（dual-stage dualpopulation evolutionary algorithm for many-objective optimization，MaOEA-DD）。与以往采用双阶段或双种群挑选个体以分别提高种群的收敛性和多样性的算法有所不同，MaOEA-DD 算法主要是通过双阶段双种群策略对权重向量进行调整，以同时提高种群的收敛性和多样性。具体而言，该算法将进化过程划分为两个阶段并且使用两个种群进行进化。在第一阶段，两个种群同时进化，其中一个种群作为辅种群，根据能量平衡的关系收集多样性较好的个体，另一个种群作为主种群，采用基于分解的方法进行进化，当主种群达到一定稳定状态后，根据权重向量与其对应的主种群个体之间的夹角，判断帕累托前沿是否规则。在第二阶段，根据第一阶段得到的帕累托前沿的形状，选择是否对权重向量进行调整，若帕累托前沿规则，则不进行调整，否则将辅种群作为主种群的权重向量指导主种群进化。其主要贡献有如下三点：

（1）提出了一种双阶段的进化过程。在第一阶段，通过权重向量与种群个体之间的角度关系判断帕累托前沿形状是否规则。在第二阶段，根据帕累托前沿的形状，选择是否对权重向量进行调整，以兼顾处理具有规则和不规则帕累托前沿的高维多目标优化问题。

（2）设计了一种双种群权重向量调整方法。其中一个主种群由预定义权重向量指导进化，另一个辅种群则负责收集多样性良好的个体。当需要调整权重向量时，将辅种群作为权重向量指导另一个种群的进化。该方法不依赖预定义的权重向量，仅调整一次权重向量，能够提高种群的多样性，同时保持种群的收敛性。

（3）本文根据自然界中多体和相互作用的物理系统趋向于均匀有序状态的特性，提出了一种收集均匀分布的种群作为权重向量的方法。该挑选过程无需额外参数，挑选的权重向量能够有效处理具有不规则帕累托前沿的多目标优化问题。

1 相关背景

定义1（高维多目标优化问题）以最小化高维多目标优化问题为例，其数学模型使用如下公式描述：

其中x=(x1,x2,…,xn)T是决策空间Ω中一个n维的决策向量，m≥3 是目标数量，F(x)是m维的目标向量。

定义2（帕累托支配关系）给定两个决策向量xa和xb，如果xa帕累托支配xb(xa≺xb)，则其对应的目标值必有：f(xa)i≤f(xb)i,∀i∈{}1,2,…,m ,且f(xa)i ＜f(xb)i,∃i∈{1,2,…,m}。

定义3（帕累托最优解）当一个解不被任何一个解支配时，则称这个解为非支配解或帕累托最优解。

定义4（帕累托最优集Pareto optimal set，PS）指的是一个包含所有非支配解或帕累托最优解的集合。

定义5（帕累托最优前沿Pareto optimal front，PF）指的是在目标空间中由PS映射而成的图形。

定义6（权重向量）一组用于衡量不同目标之间重要性的向量，通常预定义权重向量由如下公式产生：

其中，n是权重向量个数，m是目标数，C 是组合数，p是每一个坐标轴的分区数，λ是权重向量的集合。

2 MaOEA-DD算法

2.1 双阶段进化过程

采用一组预定义均匀分布权重向量的基于分解的高维多目标进化算法可以有效地处理具有规则PF的高维多目标优化问题，而无法处理具有不规则PF 的问题。采用动态调整权重向量的基于分解的高维多目标进化算法则相反。为兼顾两者，本文将进化过程分为两阶段：

第一阶段确定PF形状：在初始状态下，种群呈现混乱无序的特征，无法准确判断PF的形状，因此本文首先采用预定义均匀分布的权重向量指导种群进化，直至种群处于稳定有序的状态。而在本文中判断种群是否达到稳定有序状态的计算公式如下：

其中，f(xi)k是种群中第i个体的第k个目标值，MD代表种群中所有个体到坐标原点的曼哈顿距离。在最小化问题中，较小的MD值意味着个体离坐标原点越近，即个体越接近PF，收敛性越好[21]。因此，MD值能够一定程度上代表种群的状态。在本文中，如果相邻几代种群的MD值变化小于10-6即Δ ＜10-6，则认为该种群的收敛性已经不再变化，即达到种群达到稳定状态。

在确定种群达到稳定状态后，本文通过判断预定义权重向量与其指导的个体之间是否存在夹角来确定当前PF的形状。由于在不规则的PF上，预定义的权重向量没有考虑到PF 的形状，只考虑了两两权重向量之间的等距离关系。因此，由这些权重向量指导进化的个体无法完全分布在这些权重向量上，只能尽可能靠近它们，并与它们成一定角度。图1（a）展示了这种情况，在图中，权重向量w3与断开的PF 并没有交点，这使得由其指导进化的个体x3无法与由边界附近权重向量w4指导的个体x4保持均匀的间隙，只能分布在尽可能接近w3的PF边界上，即x3与w3会存在一定的角度。而在规则的PF 上，每个个体都能均匀分布在指导其进化的权重向量上。如图1（b）所示，每个权重向量与PF 都有交点，与其指导的个体之间不存在夹角，每个个体都分布在对应的权重向量上，即均匀地分布在PF 上。因此，在本文中，将权重向量与其指导的个体存在角度的PF判定为不规则PF，否则为规则PF。

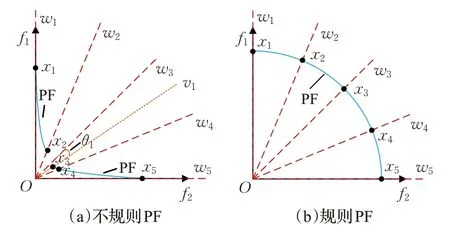
图1 在不同形状的PF上个体与权重向量的关系Fig.1 Relationship between individuals and weight vector on PF of different shapes

需要注意的是，在本文中是通过计算权重向量与其夹角最小的个体来粗略确定当前权重向量指导的个体，因为通常情况下，由当前权重向量指导的个体是与该权重向量距离最近的个体。然而，在进化过程中，即使在规则PF 上，个体与权重向量之间的角度也可能不为零度，而是存在微小角度。因此，本文以10-6作为边界值，当两者角度差小于10-6时，说明两者无夹角，否则存在夹角。此外，文中权重向量指导的个体与该权重向量之间的夹角指的是被指导个体和坐标原点构成的向量与对应权重向量之间的角度，如x3与坐标原点构成的向量v1与w3的角度θ1。

第二阶段调整权重向量：在第一阶段确定PF 形状后，在第二阶段则根据PF 的形状进行权重向量的调整。如果PF是不规则的，则进行权重向量调整，以确保种群在不规则PF上均匀分布。而如果PF是规则的，则不调整权重向量，以保持预定义权重向量在规则PF 上的优势。

具体而言，MaOEA-DD 双阶段进化过程的主要目的是通过第一阶段判断PF 的形状，然后在第二阶段选择是否对权重向量进行调整，以综合应对处理具有规则PF 和不规则PF 的高维多目标优化问题，与以往的双阶段多目标进化算法在不同阶段分别侧重于收集收敛性与多样性良好的个体的目的有所不同。同时在MaOEA-DD中阶段转换是依据种群收敛性的稳定性和权重向量与种群之间的关系这两个条件进行的，并不是依据种群的收敛性与多样性之间的关系进行的。此外，在MaOEA-DD的第一阶段中提出了一种根据权重向量指导的个体与PF 的夹角判断PF 形状的方法，在第二阶段对具有规则PF的问题和具有不规则PF的问题进行了不同的处理。

2.2 双种群权重向量调整

目前已有的权重向量调整方法大多数是权重向量的调整与种群进化同时进行，每次调整权重向量后，种群需根据新的权重向量重新进化。虽然提高了种群的分布但也严重降低了种群收敛速度，使得种群的收敛性变差。为解决此问题，本研究提出了一种使用双种群调整权重向量的方法。其中，一个种群称为主种群，使用预定义权重向量指导进化；另一个种群称为辅种群，其在进化过程中收集多样性良好的个体。这两个种群相互独立且无关。辅种群主要收集的是多样性良好的种群个体，并不受PF形状的影响，而主种群是通过权重向量指导进化的，多样性受PF形状影响，但是能够保持良好的收敛性，因此其收敛性优于辅种群但多样性差于辅种群。当种群收敛性稳定后将辅种群作为主种群的权重向量，此后便不再调整权重向量，这不仅提升了主种群在不规则PF上的多样性而且也能够保持主种群的收敛性。将辅种群转化为权重向量的具体公式如下：

其中，λi表示第i个参考向量，f(xi)m是种群中第i个体的第m个目标值，max(f(xi))表示第i个体的最大目标值。通过该公式能够将辅种群的目标值范围限定在0到1，以符合权重向量的规范。

总而言之，MaOEA-DD 双种群策略的目的是收集一个多样性良好的辅种群作为权重向量，以提高主种群的多样性。而大多数已有的双种群多目标进化算法的目的是使用一个种群收集收敛性良好的个体，另一个种群收集多样性良好的个体，然后综合挑选收敛性与多样性良好的个体。此外，MaOEA-DD 的两个种群采用了不同的进化框架进行进化，结合了不同进化框架的优点，主种群采用了基于分解的进化框架，而辅种群采用基于帕累托支配的进化框架进行，接下来的章节将会对此进行详细介绍。最后，通常权重向量是通过公式（2）计算获得的，而在MaOEA-DD中则是通过公式（4）将辅种群转化成权重向量获得的。

2.3 多样性良好的辅种群获取

高维多目标优化问题中的PF 是一个高维超曲面，这使得收集均匀分布的种群成为了一项艰巨的任务。为此本文使用了一种称为Riesz s-Energy[22]的势能在不规则PF上收集多样性良好的种群。其原理是自然界中多体和相互作用的物理系统最终会趋向于最小总势能的均匀有序状态。由于物体间势能与距离成反比，因此系统总势能较大时，系统中的物体会迅速扩散以降低势能。当系统中的物体间距离相等时，系统总势能达到最小值，此时系统中的物体停止运动。具体地，Riesz s-energy数学定义如下：

其中，E代表所有点的能量总和，这里的能量用两点之间的欧式距离表示，距离越大，能量越小则点越均匀。‖ ·‖表示欧式距离，n是点的数量，yi和yj分别代表点集R的第i、j个点，m是目标数。

由于欧式距离在高维空间中不适用[23]，所以文中两个个体之间的距离是通过计算它们对应的目标值之间的曼哈顿距离获得的。因此，在本文中的Riesz s-energy被定义为如下所示：

其中，xk表示第k个个体的决策向量，fi(xk)表示第k个个体的第i目标值，|·| 表示两者之间的绝对值。

尽管Riesz s-energy在保持点集均匀性方面表现良好，但在多目标优化中，种群分布需要同时满足均匀性和符合PF 形状（帕累托支配关系）。因此，本文在帕累托支配关系下使用Riesz s-energy。具体挑选过程如下：假设辅种群大小为N，在每次进化过程中，使用辅种群生成N个子代。从该子代和辅种群组成的2N个体集合中，选择符合帕累托支配关系且具有最小Riesz s-energy 的N个个体作为下一代辅种群。然而，从2N个个体中挑选N个符合要求的个体的时间复杂度很高。因此，在文中首先对子代和辅种群共2N个个体进行非支配排序。然后，从排名前N的个体中选取N个个体。如果有多个个体排名相同且导致前N名个体数量超过N，则从这些个体中选择与当前已选个体构成的种群的Riesz s-energy 最小的个体，直到选择的个体数达到N为止。这种选择方法类似于贪心算法，但可能不够准确。为了提高选择结果的准确性，完成上述选择后，逐一使用排名前N且未被选择的个体替换与其排名相同且已被选择的个体。如果种群的Riesz s-energy变小，则同意替换。重复此步骤，直到所有排名相同且未被选择的个体都被操作。此外，计算Riesz s-energy需重复计算两点距离。为降低计算时间复杂度，本文使用矩阵记录已计算的距离。

以上方法挑选的种群符合PF形状且均匀分布。虽然该种群的收敛性可能不佳，但将其用作主种群的权重向量指导主种群在不规则PF 上的进化方向，能够提升主种群的多样性。

2.4 算法主流程

MaOEA-DD算法处理高维多目标优化问题的主要流程与基于分解的高维多目标进化算法类似。然而MaOEA-DD 将进化过程划分为了两个阶段，并采用了两个种群进行进化，同时还对权重向量进行了调整。其算法流程图如图2所示，具体步骤如下：

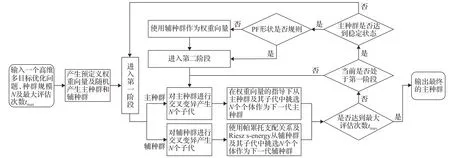
图2 MaOEA-DD算法主流程Fig.2 Main process of MaOEA-DD algorithm

输入：

步骤1一个高维多目标优化问题，种群规模N，最大迭代次数tmax。

初始化：

步骤2生成大小为N的主种群和辅种群，并创建N个预定义的权重向量。

第一阶段：

步骤3对主种群进行交叉变异，产生N个子代。

步骤4对辅种群进行交叉变异，产生N个子代。

步骤5由权重向量的指导下从主种群及其子代中挑选N个个体作为下一代主种群。

步骤6对辅种群及其子代共2N个个体进行非支配排序，挑选排名靠前且具有最小Riesz s-energy 的N个个体作为下一代辅种群。

步骤7判断是否达到最大迭代次数tmax，是则执行步骤12，否则继续进行下一步。

步骤8判断当前是否处于第一阶段，是则进行下一步，否则依次执行步骤3、5、7。

步骤9判断主种群是否达到稳定状态，如果未达到稳定状态，则返回步骤3。否则，通过权重向量与其指导的个体之间的夹角来判断PF的形状。

第二阶段：

步骤10如果第一阶段判断的PF形状是规则的，则不对权重向量进行调整，否则使用辅种群作为主种群的权重向量。

步骤11依次执行步骤3、5、7。

输出：

步骤12输出大小为N的主种群。

2.5 算法时间复杂度

针对具有m个目标的高维多目标优化问题，主种群采用了基于分解的高维多目标进化框架进行进化。其时间复杂度为O(mNT)，其中N是种群大小，T是相邻权重向量的数量，且T ＜N。对于辅种群，比较父代与子代的支配关系以及Riesz s-energy大小的时间复杂度为O(N3m)，而计算Riesz s-energy 的时间复杂度为O(N2m)。因此，辅种群每一代进化所需时间复杂度为O(N3m)。综上，MaOEA-DD 的总体时间复杂度为O(mNT+N3m)=O(N3m)。

3 实验验证

3.1 实验设置

3.1.1 测试问题及对比算法

为了验证本文所提出的算法在处理不同目标下的高维多目标优化问题时的性能，本文选择了在3、5、10 目标下的DTLZ2、DTLZ3、DTLZ5、DTLZ6、DTLZ7、W-FG4、WFG5、MAF1、MAF2、MAF3、MAF6、MAF7、IDTLZ1、IDTLZ2[24-27]共14 个测试问题来进行了实验。这组测试问题覆盖了多种高维多目标优化问题类型，包括但不限于多模态、欺骗性、难以收敛、凹形、凸形、线性、退化、不连续以及具有严重扩展PF的问题。这些测试问题的具体介绍如表1 所示。同时，本文选取来自3种不同类型的4个算法作为对比算法，这些算法分别为基于帕累托支配关系的KnEA[28]，基于指标的MaOEAIGD[9]，基于分解且采用预定义权重向量的M-OEA/D[15]，基于分解且采用了权重向量调整的VaEA[29]。

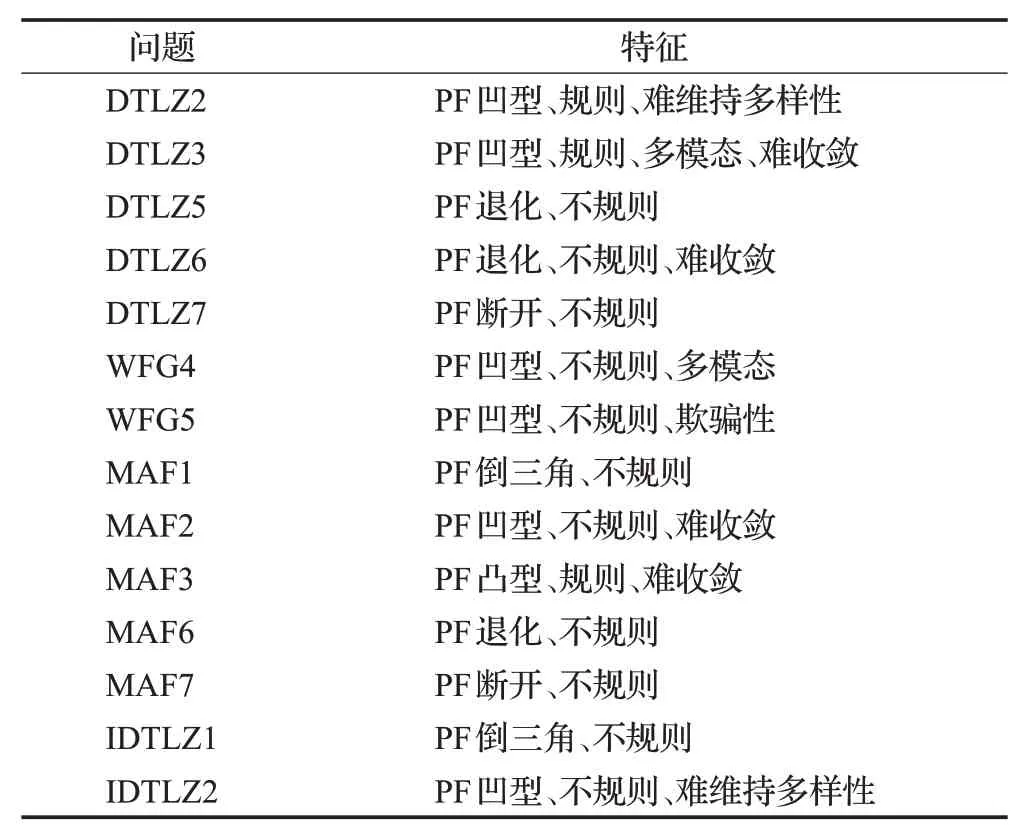
表1 测试问题Table 1 Test problems

3.1.2 参数设置

交叉和变异算子：实验中的所有算法使用的交叉算子和变异算子分别为模拟二元交叉（simulated binary crossover，SBX）[30]和多项式变异（polynomial mutation，PM）[31]。其中SBX 的交叉概率设置为1，分布指数设置为20。PM 的突变变量数量的期望值设置为1，分布指数设置为20。

种群大小、停机条件及运行次数：为了确保公平比较，在不同目标下种群的大小需要同参考点数量相同，表2展示了本文在不同目标下的种群大小。此外，在不同目标下每个算法运行的停机条件是达到对应的最大迭代次数，如表2 所示。为了确保实验结果的可靠性，每个实验算法在每个目标下的每个测试问题上都独立运行30次后取其结果的平均值及方差。

表2 不同目标数下的种群大小与最大迭代次数Table 2 Population size and maximum number of iterations for different target numbers

显著性检验：本文采用Wilcoxon 秩和检验[32]，显著性水平为0.05，对实验结果进行统计和分析。信号“+”“-”和“=”分别表示比较算法的结果显著优于、显著低于或没有显著差异于MaOEA-DD的结果。

MaOEA-DD 参数设置：MaOEA-DD 采用了基于分解的进化框架，需要在分解时对相邻的权重向量数T进行设置，T会对算法的收敛速度产生影响，由于本文在分解中采用的方法与MOEA/D 一致，因此按照MOEA/D的相关说明将T设为10。此外，MaOEA-DD在种群稳定性判断中，是通过判断相邻n代个体之间MD值不变来确定种群稳定性的，这里的n文中设置为2。通常情况MD值一代未变，则能够说明种群处于稳定状态，但是在一些具有欺骗性的问题上将n设置为1可能会出现局部最优的情况，从而错误判断种群的稳定性，在实验中发现设置为2 有助于避免这种情况的发生，且该值不宜设置过大，因为这会使得算法一直判断种群处于不稳定状态。

3.1.3 评价指标

本文采用IGD[11]作为评估不同算法综合性能的指标。该指标是通过计算真实PF上每个参考点到由高维多目标进化算法得出的近似PF上距离最近解的平均距离来近似评估最终解的收敛性和多样性。IGD 的值越小，则说明算法的综合性能越好，即收敛性与多样性越好。IGD数学表达式如下：

其中，Ptrue代表从真实PF 中获取的参考点，Pknow代表通过多目标进化算法得到的最终解集，p表示来自Ptrue的解，q表示来自Pknow的解。‖p-q‖表示p和q之间的欧氏距离，|Ptrue|表示真实PF参考点的数量。

此外，由于种群的多样性包含种群的分布广泛性及分布均匀性，因此，本文还采用了广泛性（spread）[33]和间距（spacing）[33]来对这两方面进行评估，从而评估不同算法获得的种群的多样性。具体说明如下：

Spread 是通过判断极端解与非支配边界解及非支配连续解之间的关系来评估种群分布的广泛程度。其数学定义如下：

其中，n表示种群大小，m表示目标个数，di表示所获得的非支配解中相邻解的距离，是di的平均值，是极端解与第k个边界解之间的距离。

Spacing是通过计算解之间的最小距离的标准差来确定种群的分布均匀性，该值越小种群分布越均匀。其数学定义如下：

其中，n表示种群大小，di表示第i个解到种群中其他解的最小距离，dˉ指的是所有di的均值。

由于在现实问题中，无法提前得知真实PF，从而无法使用与真实PF相关的指标来评估算法的性能，因此，本文采用HV[10]来评估不同算法在现实应用中的综合性能。HV是通过计算非支配解集和参考点包围的空间的超体积值来评估多目标优化算法的性能。其值越大则表示算法性能越好。其计算公式如下：

其中，λ表示勒贝格测度，vi代表由参考点与第i个非支配解构成的超体积，S代表非支配解集。

3.2 实验结果与分析

3.2.1 MaOEA-DD的总体性能

为了验证MaOEA-DD 在处理高维多目标优化问题时的有效性，本小节采用IGD 作为评价指标，将MaOEA-DD 与一些著名的算法进行了实验对比，实验结果如表3所示。由表3中给出的所有实验算法在不同测试问题上的IGD平均值及标准差可知，在绝大多数测试问题中，MaOEA-DD获得了最佳IGD值，相比其他竞争算法具有明显的优势。具体介绍如下：

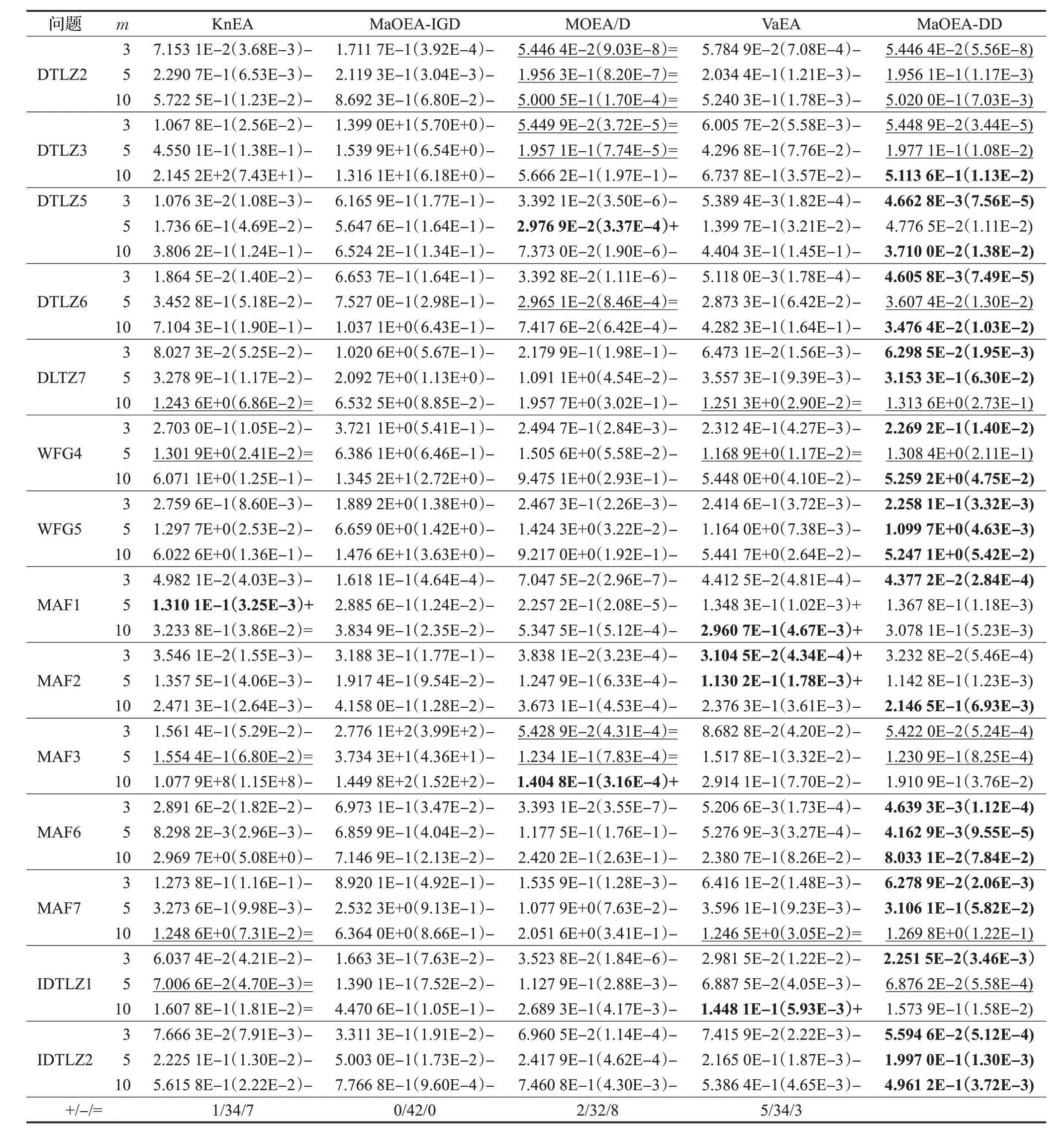
表3 所有实验算法在不同测试问题上的IGD值Table 3 IGD values of all experimental algorithms on different test problems

在处理DTLZ2、IDTLZ2、MAF1等难以维持种群多样性的问题上，由于MaOEA-DD 在面对具有规则形状及不规则形状的PF问题上分别采用了均匀分布的权重向量及辅种群作为的权重向量，因此其IGD值取得了总体最优的结果的，即使其IGD 在MAF1 的5 维、10 维稍逊于或等于KnEA和VaEA，但明显优于其他算法。

为了更直观地展示这一结果，图3 和图4 分别展示了各个算法在3 维DTLZ2 和IDTLZ2 上获得的最终种群的分布情况。

图3 所有实验算法在3维DTLZ2上获得的最终种群的分布Fig.3 Distribution of final population obtained by all experimental algorithms on 3-dimensional DTLZ2 problem

图4 所有实验算法在3维IDTLZ2上获得的最终种群的分布Fig.4 Distribution of final population obtained by all experimental algorithms on 3-dimensional IDTLZ2 problem

在图3 具有规则PF 的DTLZ2 问题上，KnEA 和MaOEA-IGD获得的种群分布在PF四周，中间位置分布稀疏，甚至没有。由于MOEA/D 也是采用预定均匀分布的权重向量指导种群的进化，因此它与MaOEA-DD在DTLZ2问题上分布一致，都分布得非常均匀。VaEA在规则的PF 上对权重向量进行了调整，因此其获得的种群在PF顶端分布的较为密集，均匀性略差于MaOEA-DD与MOEA/D。

而在图4具有不规则PF的IDTLZ2上，MaOEA-DD获得的种群分布在PF 上的各个位置，并且间隔较为均匀，而其他算法获得的种群分布较为密集。

对于DTLZ3、MAF2、MAF3、IDTLZ1等难以收敛的问题，MaOEA-DD 表现最佳。这归因于MaOEA-DD 采用了基于分解的进化策略，并且避免了选择压力的存在，从而能够有效地收敛到PF。因此，同样采用基于分解的进化策略的MOEA/D 和VaEA 也能够有效地收敛到PF。然而，由于MOEA/D和VaEA的权重向量在不同层面上并不如MaOEA-DD 的均匀，它们的IGD 值差于MaOEA-DD。另一方面，对于基于帕累托支配策略的KnEA，其IGD 较差的原因是在高维空间中选择压力不足，因此难以收敛到PF。而对于基于指标的MaOEA-IGD虽然其能够有效地收敛到PF，但是它也存在着基于指标的多目标进化算法的通病，即难以维持多样性，因此其IGD值也较差。

在DTLZ5、DTLZ6、DTLZ7、MAF6、MAF7 等具有复杂PF 的高维多目标优化问题上，MaOEA-DD 同样展现出了最佳性能，这是因为MaOEA-DD 引入了自然界中能量平衡的概念，以此收集了多样性良好的种群作为权重向量，从而能够有效地维持种群的多样性。

从图5可以直观观察到在10维MAF6问题上，所有实验算法得到的最终种群的分布情况。MaOEA-DD能够有效地收敛到PF，同时种群个体分布均匀且符合PF形状。相比之下，KnEA和VaEA无法收敛到PF，原因可能是KnEA 在高维空间失去了选择压力，而VaEA 则是因为过度调整权重向量，降低了算法的收敛性。而对于MaOEA-IGD 和MOEA/D 虽然能够收敛到PF，但是由PF过于复杂无法维持种群的多样性。

图5 所有实验算法在10维MAF6上获得的最终种群的分布Fig.5 Distribution of final population obtained by all experimental algorithms on 10-dimensional MAF6 problem

最后，在具有多模态特性的WFG4和具有欺骗性特征的WFG5 上，MaOEA-DD 取得了最佳的IGD 值。如图6 所示，MaOEA-DD 获得了良好的种群多样性，而KnEA和VaEA获得的种群只是在分布的广泛程度上表现较好，种群个体之间的间隔并不均匀，存在许多空白区域。相比之下，MaOEA-IGD与MOEA/D则是因为没有有效处理具有多模态特性的问题方法，因此它们获得的种群分布密集，容易汇聚到一点上。

图6 所有实验算法在10维WFG4上获得的最终种群的分布Fig.6 Distribution of final population obtained by all experimental algorithms on 10-dimensional WFG4 problem

至此，这些结果已经证实了MaOEA-DD 对多种高维多目标优化问题上的有效性。

3.2.2 权重向量调整方法的有效性验证

为了评估本文提出的权重向量调整方法在规则和不规则PF 上是否能够获得分布性良好的解，本小节采用Spacing以及Spread作为评价指标，将MaOEA-DD与同样采用权重向量调整方法的VaEA进行了实验比较，实验结果见表4。

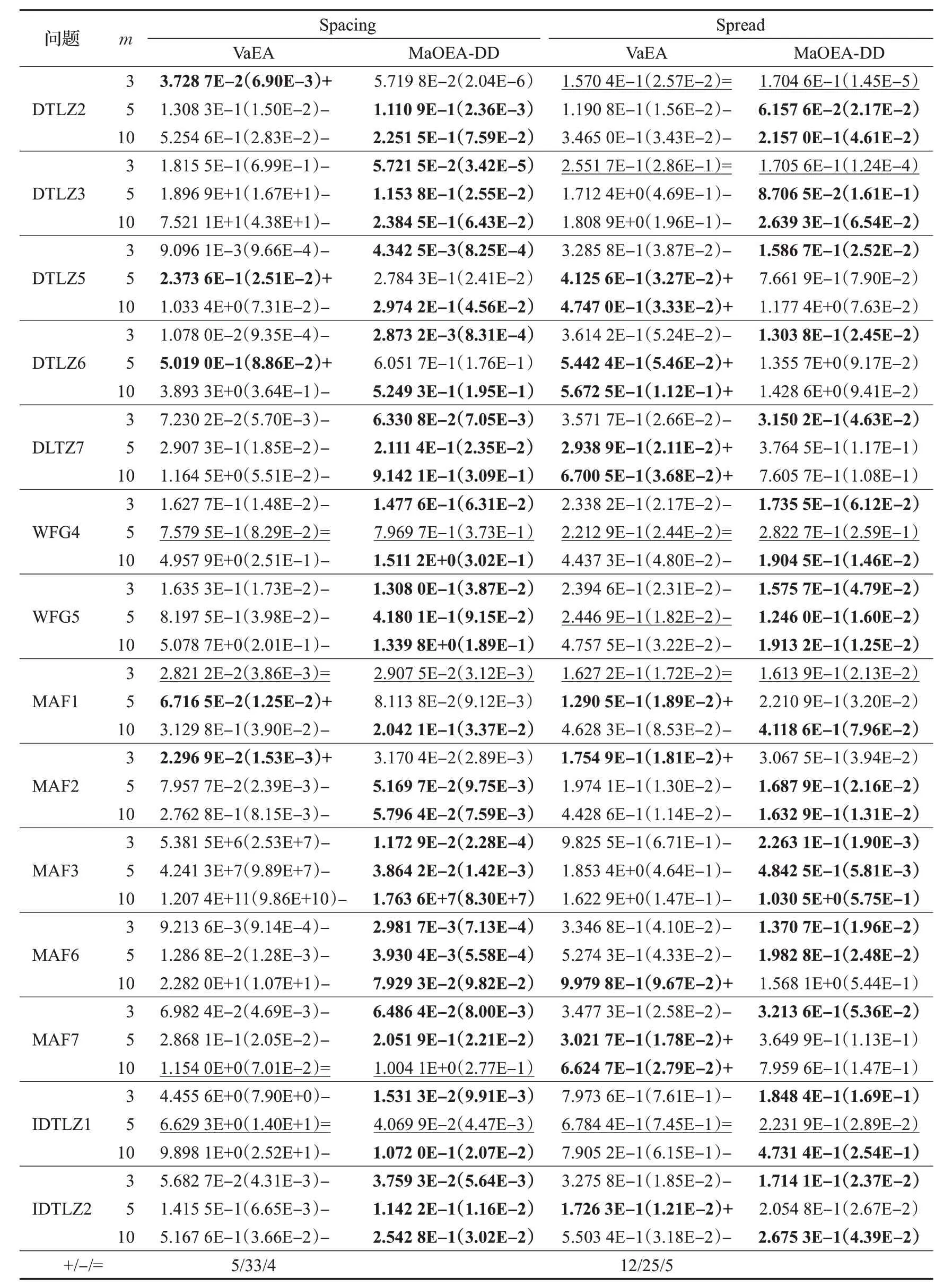
表4 所有实验算法在不同测试问题上的Spacing和Spread值Table 4 Spacing and Spread values of all experimental algorithms on different test problems

根据表4 中给出的所有实验算法在不同测试问题上获得的Spacing 和Spread 的平均值及标准差，可得出MaOEA-DD 在Spacing 以及Spread 指标上均表现出最佳结果。具体说明如下：

规则PF：在DTLZ2、DTLZ3、MAF3 等具有规则PF的测试问题中，MaOEA-DD 的Spacing和Spread值几乎全优于VaEA，这意味着MaOEA-DD获得的种群在分布的均匀性与广泛性几乎全优于VaEA，即MaOEA-DD获得的种群多样性更优。这归因于MaOEA-DD的双阶段进化过程，使其在第一阶段中准确地判断了PF 的形状是规则的，因此其并未对权重向量进行调整，从而保持了预定均匀分布的权重向量能够在处理具有规则PF的问题上获得良好多样性的优点。而VaEA 在规则的PF上对权重向量进行了调整，因此导致了其在规则PF 上的获得的解的多样性要差于MaOEA-D。

不规则PF：在DTLZ6、DTLZ7、WFG4、WFG5、MA-F3、MAF2、MAF6、MAF7、IDTLZ1、IDTLZ2 等具有不规则PF的问题上，MaOEA-DD的Spacing和Spread值分别取得25 个和18 个最优结果，而VaEA 的Spacing 和Spread值仅分别取得4个和12个最优结果。可知MaOEA-DD的Spacing 最优结果个数远多于VaEA，即MaOEA-DD获得的种群在分布均匀性上优于VaEA获得的种群。这是因为MaOEA-DD 采用Riesz s-Energy 收集的种群作为的权重向量，可以获得分布更均匀的效果。而VaEA采用的是最大向量角原则收集的权重向量，该原则在凸问题等复杂问题中，存在着两两个体之间角度均匀并不代表它们之间的距离也均匀的问题，因此VaEA获得的种群均匀性会较差。对于MaOEA-DD的Spread最优结果个数仅比VaEA 的Spread 最优结果个数多6 个，这是因为种群分布的广泛程度会受种群收敛性的影响。如在图5 的10 维MAF6 问题上，VaEA 获得的种群并未收敛，因此其分布广泛程度必然会远优于MaOEA-DD，但这并不能说明在收敛的情况下MaOEA-DD的广泛程度不如VaEA。类似的情况也出现在DTLZ5 和DTLZ6上。即便不考虑这些情况，MaOEA-DD 获得的种群的分布广泛程度仍优于VaEA。综上所述，MaOEA-DD获得的种群分布的均匀性及广泛程度均优于VaEA，即MaOEA-DD获得的种群多样性优于VaEA。

MaOEA-DD获得的种群不仅在具有规则PF的高维多目标优化问题上多样性优于VaEA，并且在具有不规则PF的高维多目标优化问题上多样性也优于VaEA，这说明了本文所提出的权重向量调整方法比VaEA所采用的权重向量调整方法更有效，能够同时处理具有规则PF和不规则PF的高维多目标优化问题。

3.2.3 收敛速度分析

为探究MaOEA-DD与其他对比算法在收敛速度方面的差异，本小节记录了不同算法在不同测试问题下随着迭代次数增加，其IGD 值的变化情况。

具体变化见图7，说明如下：

图7 5种算法在10维DTLZ2、DTLZ3、MAF6和IDTLZ2上IGD值的变化Fig.7 Variation of IGD values of 5 algorithms on 10-dimensional DTLZ2，DTLZ3，MAF6，and IDTLZ2

规则PF：如图7（a）所示，在较易收敛且具有规则PF 的DTLZ2 问题上MaOEA-DD 与MOEA/D 均在迭代3 000次左右收敛，这是因为MaOEA-DD在双阶段进化过程中将DTLZ2问题识别为具有规则PF 的问题，采用了预定义的权重向量进化，因此MaOEA-DD与MOEA/D的收敛速度相同，同理在图7（b）较难收敛且具有规则PF 的DTLZ3 问题上MaOEA-DD 与MOEA/D 的收敛速度也相同，在迭代1 000 次左右收敛。而KnEA 虽然在DTLZ3 中IGD 变化幅度较大，但其收敛速度在DTLZ2和DTLZ3 都是最快的。对于MaOEA-IGD 其收敛速度仅次于KnEA，无论在DTLZ2还是DTLZ3均在迭代500次左右收敛。由于VaEA在进化过程中频繁调整权重向量因此其收敛速度最慢。因此在规则PF 上所有算法的收敛速度排名为KnEA>MaOEA-IGD>MaOEA-DD=MOEA/D>VaEA。

不规则PF：如图7所示不论是在难收敛且具有不规则PF的MAF6问题上还是在较易收敛且具有不规则PF的IDTLZ2 问题上MaOEA-IGD 的收敛速度都是最快的。如图7（c）所示，MOEA/D收敛速度仅次于MaOEAIGD，而KnEA 虽然IGD 变化幅度较大，但是其值在迭代200 次左右在固定的范围摆动，其收敛速度快于MaOEA-DD。MaOEA-DD 在迭代350 次左右收敛，速度优于VaEA，但是因为MaOEA-DD对权重向量进行了调整因此收敛速度慢于MOEA/D。对于VaEA，其收敛速度最慢，在迭代4 000 次时才取得最小值。而在图7（d）较易收敛且具有不规则PF 的IDTLZ2 问题上VaEA收敛速度仅次于MaOEA-IGD。虽然KnEA 在迭代100次后IGD 值在浮动，但是其浮动幅度较小，因此KnEA收敛速度在IDTLZ2 上排名第三。即便MOEA/D 与MaOEA-DD都在迭代4 000次后取得最小IGD值，但是MOEA/D的IGD值变化幅度较小，所以其收敛速度快于MaOEA-DD。因此，在不规则PF 上算法收敛速度排名为MaOEA-IGD>MOEA/D=KnEA>VaEA>MaOEA-DD。

综上所述，所有实验算法在具有规则及不规则PF的问题上综合收敛速度排名为MaOEA-IGD≥KnEA>MOEA/D>VaEA≥MaOEA-DD。需要注意的是，这只是对所有实验算法的收敛速度粗略的排名，具体每个算法的收敛速度需要根据实际问题进行判断。虽然MaOEA-DD 的收敛速度较慢，但其收敛性最优。因此其在解决高维多目标优化问题中仍有着竞争优势。

3.2.4 汽车碰撞安全设计优化

为了验证MaOEA-DD在现实世界优化问题中的实用性，本小节将MaOEA-DD 与其他对比算法分别应用在汽车碰撞安全设计优化问题[34]上。该问题的主要目的是通过对汽车结构进行优化，以满足碰撞安全性标准。为确保汽车满足碰撞安全性标准，需要对汽车结构的重量、加速度特性和脚板侵入这三个目标进行优化，其中这三个目标相互冲突并且需要同时最小化，是一个高维多目标优化问题。在对该问题应用实验算法进行优化时，种群大小统一设置为91，迭代次数设置为1 500，并且每个算法在该问题上独立运行30 次取平均HV 值作为实验结果。实验结果如表5 所示。在汽车碰撞安全设计优化中，MaOEA-DD 获得了最优的HV 值，虽然VaEA 获得的HV 值与MaOEA-DD 相近，但是随着目标数的增加，PF 越来越复杂，MaOEA-DD 与VaEA 的差距可能会逐渐增大。KnEA 的性能虽然不如MaOEA-DD和VaEA，但优于其他算法。对于MOEA/D，由于其采用了固定的权重向量进行进化，因此其性能远不如MaOEA-DD，这也验证了本文权重向量调整方法的有效性。由于MaOEA-IGD难以保持种群的多样性，其性能最差。由此可得，MaOEA-DD 在现实优化问题中具有一定的实用性。

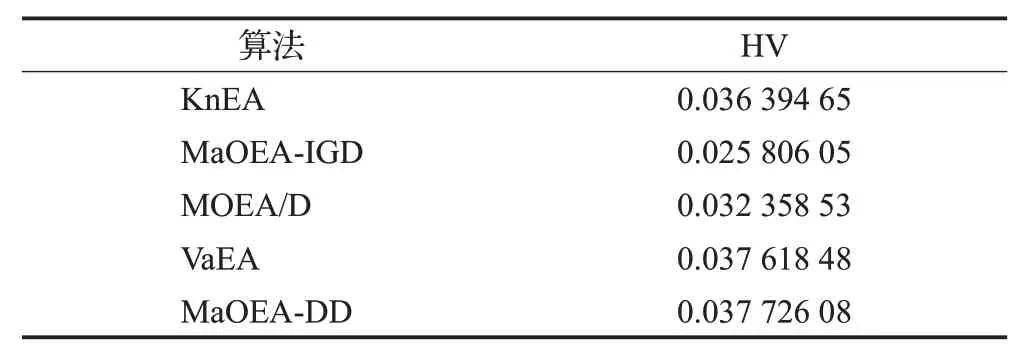
表5 所有算法在汽车碰撞安全设计优化中获得的HV值Table 5 HV values obtained from all algorithms in optimization of crash safety design for vehicles

4 结束语

为了在具有规则和不规则帕累托前沿的高维多目标优化问题中获得收敛性和多样性良好的种群，本文提出了一种面向高维多目标优化的双阶段双种群进化算法。该算法将进化过程划分为两个阶段，以同时考虑种群在具有规则和不规则帕累托前沿的问题上的多样性。在处理具有不规则帕累托前沿的问题时，该算法使用了一个辅种群收集多样性良好的个体作为权重向量，一个主种群正常进化，避免了在权重向量调整时主种群的收敛性下降。此外，该算法还借鉴自然界中能量平衡的概念来选择多样性良好的辅种群作为权重向量。为了验证该算法的性能，将该算法与其他4个著名的算法进行了实验对比，实验结果表明，本文算法能够有效地处理不同类型的高维多目标优化问题。此外，本文提出的权重向量调整方法在与其他权重向量调整方法进行的实验对比中也被证实是有效的。然而，本文算法获得的种群在不连续的帕累托前沿上的分布广泛性并没有达到最优。针对该问题，下一步将设计一种保护边界解的方法以提高种群的分布广泛性。