针对光伏发电功率预测的LSTformer模型

刘世鹏，宁德军，马 崛

1.中国科学院上海高等研究院，上海 200120

2.中国科学院大学，北京 100049

光伏发电产业在近些年迎来了高速的发展，根据国际能源机构（IEA）的数据，全球光伏装机量的增长速度高达49%，预计在2050 年全球光伏发电在总发电量的占比将达到16%[1]。与传统能源（如火电、水电、核电等）具有连续性和可调性的特点不同，光伏发电的出力受气候、气象、地理、电站设计等因素的影响，具有非常显著的周期性、随机性和波动性等特点。因此，光伏行业的发展虽然迅速，但仍然给电力系统带来了很多挑战，尤其是在如何能够在维持电力系统安全平稳运行的同时，完成大规模光伏发电设备及站点的并入，顺利消纳大量光伏发电功率。为了解决该问题，需要制定足够合理且精确的电网调度策略，然而电网调度策略包含众多操作，如发电计划指定、削峰填谷等。为了准确地完成这些操作，需要发电预测数据作为基础，因此光伏发电功率预测算法研究成为了亟待优化的任务。

针对光伏发电功率预测问题，国内外诸多学者展开了大量研究，目前主流的预测手段主要集中在传统随机学习与深度学习方法。在传统随机学习领域，支持向量机（support vector machine，SVM）和支持向量回归（support vector regression，SVR）普遍被用于可再生能源预测领域[2]。文献[3]提出了一种基于SVM 的短期太阳能预测模型，该模型使用历史大气透射率和其他气象数据作为输入。文献[4]提出基于支持向量回归模型预测水平面总辐照度（global horizontal irradiation，GHI），预测范围为1 h，具有最佳的预测性能。

在深度学习领域中，循环神经网络结构（recurrent neural network，RNN），如长短期记忆网络（long short term memory，LSTM）、门控循环单元（gated recurrent unit，GRU）、Transformer 系列模型等，被广泛用来分析和预测时间序列数据，比如金价预测[5]、交通流量[6]、语音分类[7]等。而光伏发电功率预测也可以看作时序数据预测的一种，LSTM已被用于预测短期GHI或太阳综合负荷[8-9]。为了在尽量保证精度的同时减少训练时间，GRU网络被应用于短期光伏发电功率预测[10-12]，文献[13]表明利用历史数据结合GRU模型在预测光伏发电功率的实验中表现很好。

当前的研究主要集中在预测几小时内的数据，而根据GB/T 33590.2-2017[14]，光伏发电功率预测需要预测24 h 甚至更长的时间范围。目前光伏发电功率预测领域常见的深度学习模型大多为点到点模型或者序列到点模型。预测的结果为下一个时刻的光伏发电功率值。24 h 光伏发电功率预测的结果为次日光伏发电功率的序列，而非一个数值，因此预测难度更大。现有的模型大多采用多步迭代来实现序列的预测，然而由于多步迭代存在误差累积现象，其预测精度往往会随着步长的增加而下降。因此Transformer 系列模型[15-16]开始逐渐应用到时间序列预测问题上。Informer[17]甚至将光伏发电功率预测问题作为其模型的一个算例，但Informer模型并没有充分利用相应的天气数据。

基于上述分析，目前的光伏发电功率预测主要有两个难点：一是传统模型在进行多步预测时，会存在误差累积现象，误差较大，而Transformer系列模型的预测结果难以充分利用天气数据。二是难以同时提取多尺度的时序特征。针对以上问题，提出了一种基于长短期时序数据融合的Transformer生成式预测模型：LSTformer。

本文的主要贡献如下：

（1）针对光伏发电功率多步预测的误差累积问题，提出LSTformer预测模型，该模型基于传统Transformer结构，并针对光伏发电数据的特殊性进行了优化。

（2）针对当前模型提取时序特征困难问题，设计全新的特征融合器，利用其中的时序分析模块、时序特征融合模块和多周期嵌入模块进行数据融合。通过多种方法提取多时间尺度的时序特征，并充分融入到预测模型输入中。

（3）设计时间卷积前馈单元，在编、解码的过程中进一步提取数据的时序特征。

1 光伏发电功率数据时序特征

在过往的研究中，光伏发电功率预测问题通常被定义为时间序列预测问题，时间序列往往具有一定程度的自相关性。但是随着采样粒度增大，光伏发电功率数据的自相关性会减少，受外界天气因素的影响增大[18]。根据GB/T 33590.2-2017[14]，光伏发电功率数据的采样粒度为15 min，受天气因素影响的程度较大，但具有一定的自相关性，同时天气因素的变化具有一定的规律性和偶然性，因而光伏发电功率数据体现出了一定的周期性、波动性和偶然性。

如图1 所示，随机选取某光伏电站5 天的发电功率历史数据进行可视化处理，根据可视化结果（图1），可以推断出在连续5天的历史数据中，体现了光伏发电周期性与波动性的特点。

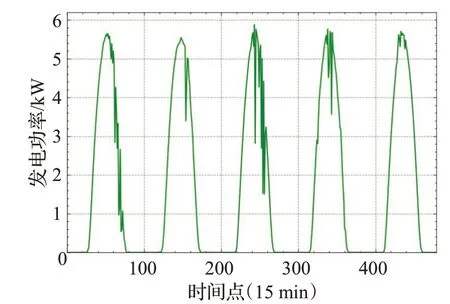
图1 连续5天的15分钟数据Fig.1 15 min data for five continuous days

如图2所示，为了探究光伏发电功率数据的长期时序特征，本文利用季节性预测模型的经典技巧，选取某光伏电站连续5 年8：30 时刻的发电功率历史数据进行可视化处理。根据可视化结果（图2），虽然光伏发电数据呈现出了更大的波动性，但是仍然可以看出其具有一定的周期性。

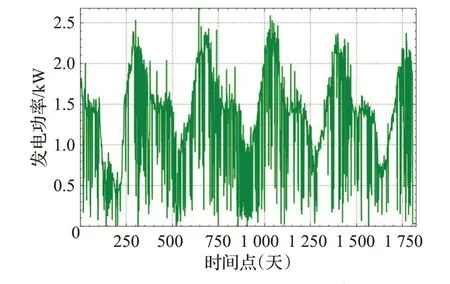
图2 连续5年的8：30时刻数据Fig.2 8：30 data for five continuous years

结合图1、图2呈现的信息，光伏发电功率历史数据不仅在短期内具有时序特征，在长时间维度下也具有一定的时序特征。考虑到这种长时间维度（如图2中周期接近365 天）下的优化问题，如何提取这种时间依赖关系是本文需要解决的问题。针对类似问题，长短时间序列网络（long-and short-term time-series network，LSTnet）模型[19]利用跳跃-循环神经网络（skip-recurrent neural network，skip-RNN）结构可以捕捉更长期的时序特征。

2 相关技术

2.1 LSTM

LSTM 网络的本质是一种改善了长期依赖问题的循环神经网络（recurrent neural network，RNN）。LSTM的网络结构与常规RNN 网络相似，都是具有重复模块的链式结构，在预测过程中，LSTM 同时更新内部状态ct和外部状态ht，更新的方式主要通过遗忘门、输入门和输出门三个门，其中遗忘门ft的作用主要是控制t-1 时刻的内部状态ct-1需要遗忘的信息；输入门it的作用主要是控制t时刻下候选状态c͂t需要留存下来的信息；输出门ot的主要作用是控制t时刻下ct中需要选择什么信息传输至外部：

式中，dt表示t时刻的输入，it表示输入门，ft表示遗忘门，ot表示输出门，ht-1是上一时刻的外部状态，c͂t是候选状态，ct-1是上一时刻的内部状态，ct是这一时刻的内部状态，ht是这一时刻的输出。

2.2 GRU与skip-GRU

GRU网络[20]是LSTM网络的变种，将LSTM单元的三个门合并为两个门，在不损失精度的情况下降低模型的复杂度：

式中，dt表示t时刻的输入，rt表示重置门，zt表示更新门，ht-1是前一时刻的隐藏状态，h͂t是这一时刻的候选状态，ht是这一时刻的输出。

因为传统GRU 模块不善于提取长期时序特征，skip-GRU模块跳过连接层，通过间隔采样的方式，在采样序列长度不变的情况下，可以回看更长的时间，以此来捕获长期特征：

式中，dt表示t时刻的输入，rt表示重置门，zt表示更新门，p是采样的间隔，ht-p是p个时刻前的隐藏状态，h͂t是这一时刻的候选状态，ht是这一时刻的输出。

2.3 自注意力机制与稀疏自注意力机制

传统自注意力机制的计算公式如下：

式中，WQ、WK、WV为三个权重矩阵，在进行随机初始化后，根据式（15）～（17）生成三个向量Q、K、V，然后根据式（18）计算出经过注意力机制加权后的结果A(Q,K,V)，该结果包含了所有输入数据的信息，但是时序数据普遍存在长尾效应，并非所有信息都是有意义的[17]，故而LSTformer 尝试引入Informer 模型中的稀疏注意力机制。

稀疏注意力机制中提出利用KL散度计算每个query的稀疏性度量：

基于计算出的稀疏性度量，通过每个k只关注u个主要q来实现稀疏注意力机制：

其中，是大小与q相同的稀疏矩阵且其只包含稀疏度量M(q,K)下的top-u个q。

2.4 问题定义

LSTformer解决光伏发电功率预测问题的思想是将其抽象为一个多步时间序列预测结合的问题。即定义为输入为光伏发电历史数据及其历史天气数据，即一个I×n的时间序列，输出为预测的光伏发电功率数据，即一个O×1 的时间序列，其中I为输入序列长度，O为输出序列长度。

3 LSTformer模型

针对光伏发电功率数据时序特征，本文提出了LSTformer预测模型，模型的结构如图3所示，LSTfomer主要结构包含三个模块：特征融合器、编码器和解码器。LSTfomer在特征融合器中提出了创新性的时序分析模块和时序特征融合模块，充分融合光伏发电数据多时间尺度下的时序特征。LSTfomer的编码器和解码器采用基于传统Transformer 架构的编码器-解码器结构，提出了TCNForward模块并引入了一步解码的生成式预测结构以避免误差累积现象。

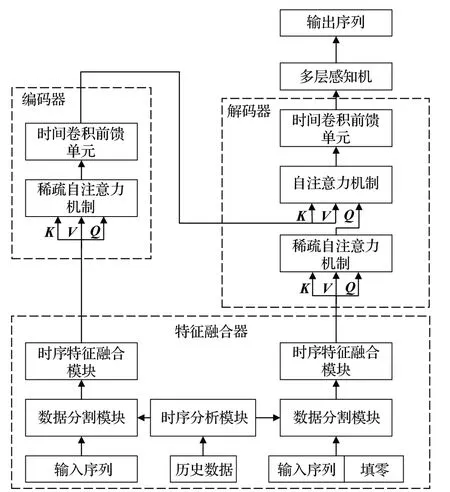
图3 LSTformer模型结构Fig.3 Structure of LSTformer model

在LSTformer 预测模型中编码器模块与解码器模块都采用多层结构设计。以一个共有N层Encoder 模块和M层Decoder模块的LSTformer模型为例，其算法描述如算法1所示。

算法1LSTfomer预测算法

3.1 特征融合器

LSTformer 中的特征融合器的结构如图4 所示，主要包含两个创新模块：时序分析模块和时序特征融合模块。

图4 特征融合器结构Fig.4 Structure of feature fuser

3.1.1 时序分析（TSA）模块

时序分析模块将根据相关性与周期性的分析结果，对变量进行筛选：

由图1 和图2 可知，光伏发电功率数据虽然波动性很强，但仍然存在周期性，而且在一定时间范围内很可能存在不同周期性，本文选择傅里叶变换对伏发电功率数据及其影响因素数据的曲线进行周期性分析[21]，旨在得到不同周期曲线的波动周期，为分析光伏发电功率预测提供一定程度的参考，首先利用以下公式求解傅里叶变换结果，将数据映射到频域：

式中，X(k)表示傅里叶级数，x(n)表示傅里叶系数，k表示指频域上的x坐标，N表示周期，WnKN表示为复变函数，复变函数的计算方式如下：

继而通过计算变换幅值的峰值即光伏发电功率数据的周期，每组数据可能存在多个周期，本文中仅取前两个周期，即首要周期及次要周期。

光伏发电功率与大量的天气因素具有相关性，本文选择利用皮尔逊相关系数进行相关性分析，皮尔逊相关系数可以计算两组任意数据x、y彼此的相关程度计算公式如下：

3.1.2 时序特征融合（TSFF）模块

传统Transformer 系列模型虽然能够通过不断加长编码器输入数据的长度来提取长期时序特征，但是采取这种手段将会带来大量冗余信息，导致计算量与计算时间的爆炸性增长。因此，本文提出时序特征融合模块，使得LSTformer 模型中编码器和解码器能够在不输入超长数据情况下充分提取到数据的时序特征。在时序特征融合模块中分别使用LSTM 模块、skip-GRU 模块、多周期嵌入模块从多个时间尺度出发，充分提取数据的时序特征。

式中TSFF(·)的计算方法如下：

将短周期时序相关数据ds、长周期时序相关数据dl分别传入时序特征融合模块中的LSTM 网络和skip-GRU网络进行预测，其中LSTM网络的预测结果充分利用了短期时序特征，skip-GRU 网络充分利用了长期时序特征：

将两个特征提取结果fl、fs、非周期输入数据dt传入多周期嵌入模块：

LSTM 和skip-GRU 单元分别提取了数据的短期时序特征和长期时序特征，但是其涵盖的时间范围不足以提取到足够长期的时序特征，故而本文提出了多周期嵌入模块，配合LSTM、skip-GRU，使得时序特征融合模块能够充分融合多个时间尺度下的时序特征。

多周期嵌入模块的组成如图5所示，主要包括数据投影、位置编码、周期编码、时间编码。

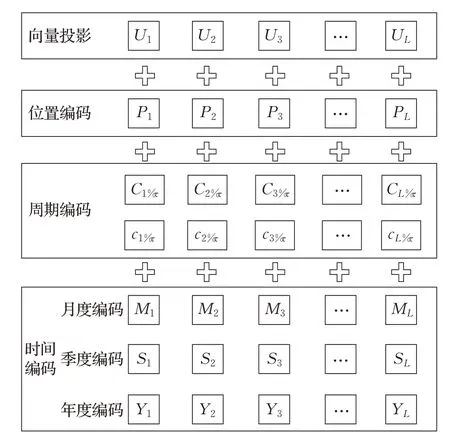
图5 多周期嵌入模块结构Fig.5 Structure of CycleEmbed

其中，数据投影是根据相关性与周期性分析的结果，将输出的数据映射到dmodel维的向量，进行维度对齐，对齐工具为一维卷积滤波器。

位置编码是传统Transformer的位置编码。

周期编码是依据周期性分析计算的结果划分，τ为周期数据步数，由周期性分析的结果T1、T2与数据采样时间粒度g决定，即τi=Ti/g，然后将根据τi的结果对输入数据的周期信息进行编码操作，即周期编码中共有τi种结果，。C和c表示两个不同周期编码的结果。

时间编码则是在编码中添加月度、季度与年度信息，以此来提取更长期的时序特征。这样数据的月度、季度与年度信息将会伴随着嵌入操作传入编、解码器中。LSTformer 选用一步解码的生成式预测方式，所以多周期嵌入模块也可以提前将一些时间信息传入待预测序列中。

综合四个部分的结果，最终多周期嵌入模块的输出结果即编码器的输入：

3.2 编码器模块

编码器的结构采取传统Transfomer多层网络结构，每层编码器主要由两个部分组成，分别是稀疏注意力单元和时间卷积前馈单元。

与传统Transformer 系列模型的线性层不同，本文设计了时间卷积前馈单元，在编码器中进一步提取数据的时序特征，其结构如图6所示。

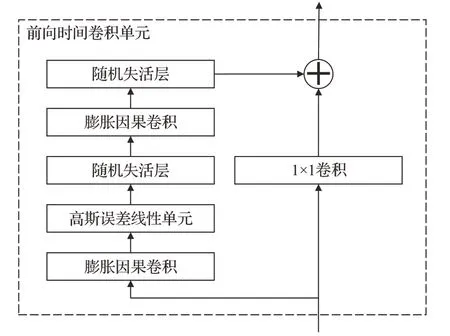
图6 时间卷积前馈单元模块结构Fig.6 Structure of TCNForward

TCNForward单元主要通过堆叠多个膨胀卷积令该单元网络捕捉不同周期之间的时序关系，并通过残差链接，使得网络能够跨层传输原始数据依赖信息表达，最大限度地关联融合长周期时序特征与短周期时序特征（即通过多层卷积得到的高阶特征与低阶特征）。

3.3 解码器模块

传统的Transformer 结构通过编码的并行计算提高了运算效率，但是在预测过程中，掩码机制下的解码器仍旧需要通过迭代的方式进行预测，直到输出指定长度的序列。在这一解码过程中，误差累积的现象难以避免，本文考虑引入Transformer 生成式预测模型普遍使用的一步解码操作：

解码器预测的过程与编码器类似，但是比编码器多了一个自注意力层。在该层中，Q是来自于解码器稀疏注意力单元的计算结果，而K和V则来自于编码器。

最终待预测序列通过一个多层感知机（multilayer perceptron，MLP）完成一步解码：

4 实验与分析

4.1 数据准备及预处理

4.1.1 数据准备

该数据集包括在澳大利亚[21]的一个太阳能农场中进行的2015 年至2016 年的光伏发电开源数据集，时间间隔为15 min，每日有96 个数据点，共有70 176 个样本，每个样本包含13 个数据，分别为时间戳、接收到的有功能量、当前阶段平均值、有功功率、性能比率、风速、天气温度摄氏度、天气相对湿度、全球水平辐射、漫反射水平辐射风向、天气日降雨量、辐射全局倾斜、辐射漫反射倾斜，测试集使用2016年11月、12月的数据。

两年的所有数据如图7 所示，x轴为天数，y轴为每天96 个时间点（采样粒度为15 min，24 h 的数据共包含96个事件点），z轴为光伏发电功率数据。

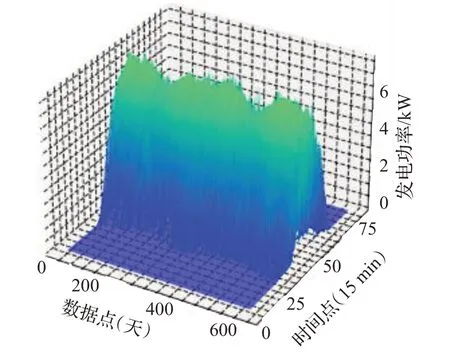
图7 光伏发电功率历史数据集Fig.7 Historical dataset of photovoltaic power

4.1.2 数据预处理

由于各变量之间的量纲并不完全相同，因此在进行预测时需要先进行线性归一化处理，其转换函数为：

式中，xnorm是数据进行线性归一化之后的预处理结果；xi是需进行归一化的变量输入值；max(xi)是原始数据集中xi所属变量的最大值；min(xi)是原始数据集中xi所属变量的最小值。

4.2 评价指标

为验证模型的预测精度，采用均方根误差（mean square error，MSE）、平均绝对误差（mean absolute error，MAE）作为模型性能的评价指标，其具体计算公式为：

Xi为测试集的第i个数据点出力实际值；X̂i为第i个数据点的出力预测值；N为测试集样本总数。

4.3 实验环境及参数设置

实验环境采用Intel i7-9700K 处理器，NVIDIA GeForce RTX 3080 Ti 显卡，算法模型采用Python 3.8作为编程语言，基于开源机器学习框架pytorch 搭建模型相关网络。本文采用随机搜索方法确定最终的超参数设置，最终的超参数设置如表1所示。

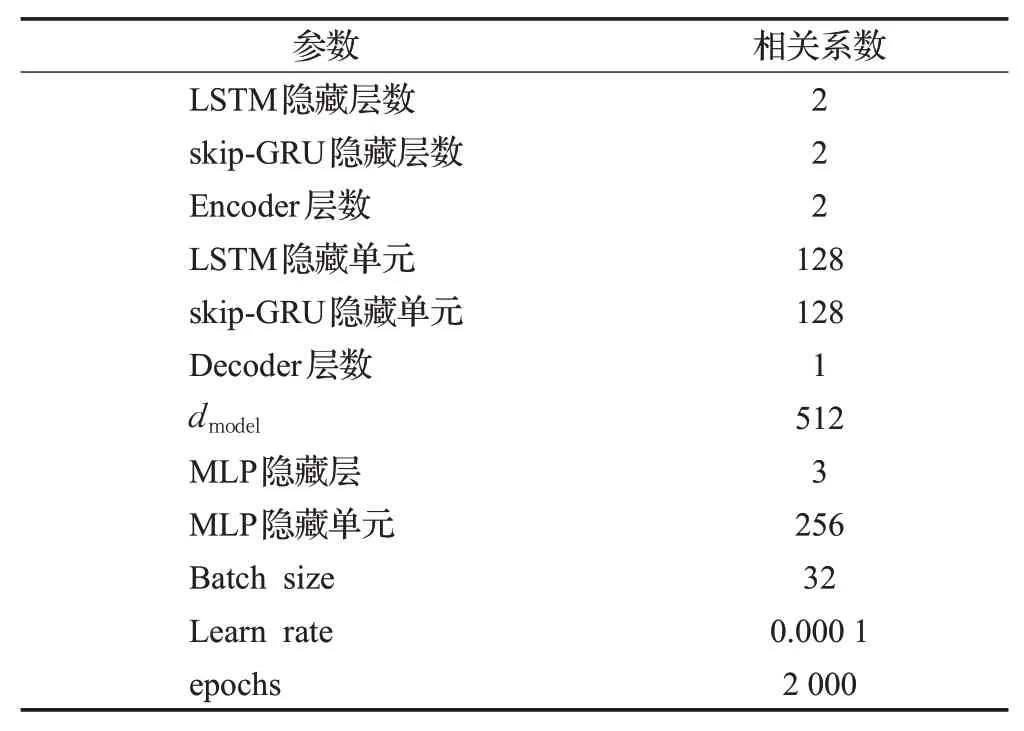
表1 模型参数设置Table 1 Model parameters setting

4.4 结果与讨论

4.4.1 时序分析结果及讨论

特征融合器中的时序分析模块包含相关性分析分析与周期性分析两部分，对光伏发电功率相关性分析的结果表2所示。

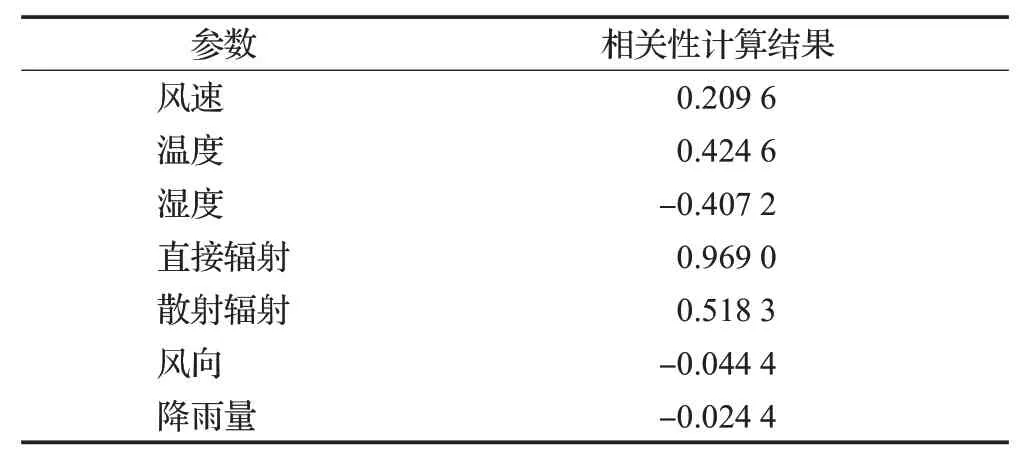
表2 相关性分析结果Table 2 Results of correlation analysis

根据表2 可以看出，光伏发电功率与直接辐射强度、散射辐射强度、温度、风速成正相关，与湿度、风向、降雨量成负相关，根据其数值大小，可以看出直接辐射强度、散射辐射强度、温度、湿度、风速等变量与光伏发电功率具有一定的相关性，这些影响因子都会对光伏发电功率产生一定程度的影响，影响能力依次递减。风向与降雨量这两个因素的相关性计算结果过低，虽然呈一定的负相关，但本文将其视为不具有相关性的因素。

对光伏发电功率周期性分析的结果表3所示。

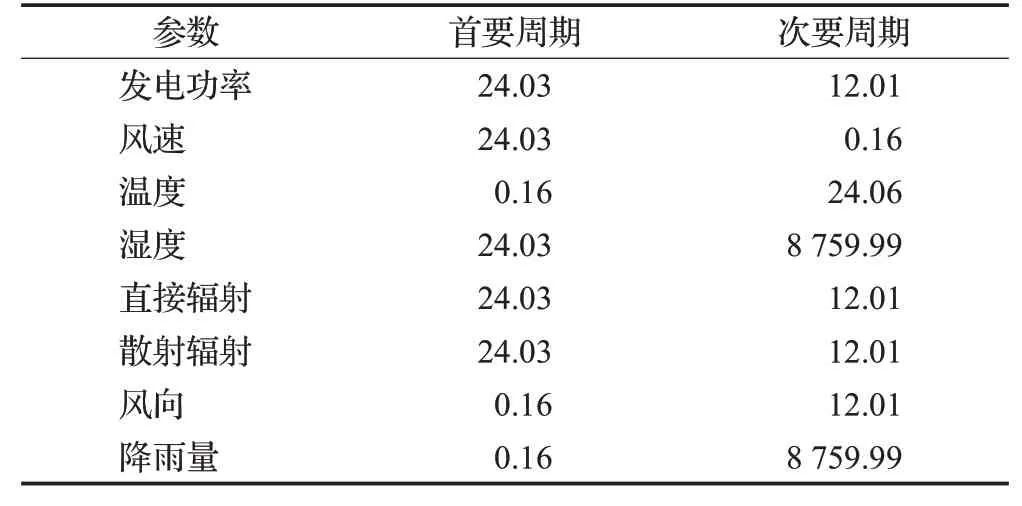
表3 周期性分析结果Table 3 Results of periodicity analysis 单位：h

根据表3可以看出，在各个数据主要呈现出的两个周期之中，发电功率、风速、湿度、温度直接辐射、散射辐射都包含半天至一天左右的周期，根据时序分析模块的划分，将其处理为短期时序相关数据；湿度、降雨量都包含一年左右的周期，将其处理为长期时序相关数据；温度、风速、风向、降雨量都包含0.16 h 的周期，将其处理为非时序相关数据。

由相关性分析可以筛选出直接辐射强度、散射辐射强度、温度、湿度、风速五个影响因子，结合周期性分析的结果，输入数据的划分结果为：包含发电功率、湿度、降雨量的2 880 个连续数据点作为长期时序相关数据；包含发电功率、风速、湿度、温度直接辐射、散射辐射的288个连续数据点作为短期时序相关数据；包含发电功率、温度、风速的96个连续数据点作为非时序相关数据。

4.4.2 不同预测步数的预测结果讨论

LSTM网络在进行光伏功率短期预测时，随着预测步数的增加，会逐渐体现出误差累计的现象，为了探究各模型在不同预测步数下的预测表现，本文选取了LSTM、skip-GRU、Transformer、Informer 与本文进行对比，结果如表4所示，由结果可见，在预测步数为1时，五种模型的MSE 误差相差不大，随着预测步数的增加，LSTM模型前期误差增加速度极快，但是后面的误差浮动不大，前期误差累积现象明显，后期误差过大不能准确预测结果。采用生成式预测方法的Informer 模型误差累计现象相对不明显，但是误差相对于LSTformer较大。本文提出的LSTformer模型不仅误差累积程度小，而且全程都具有最低的MSE误差。为了更直观地观察各模型之间的误差累积现象，将预测结果进行可视化展示，可视化结果如图8所示。

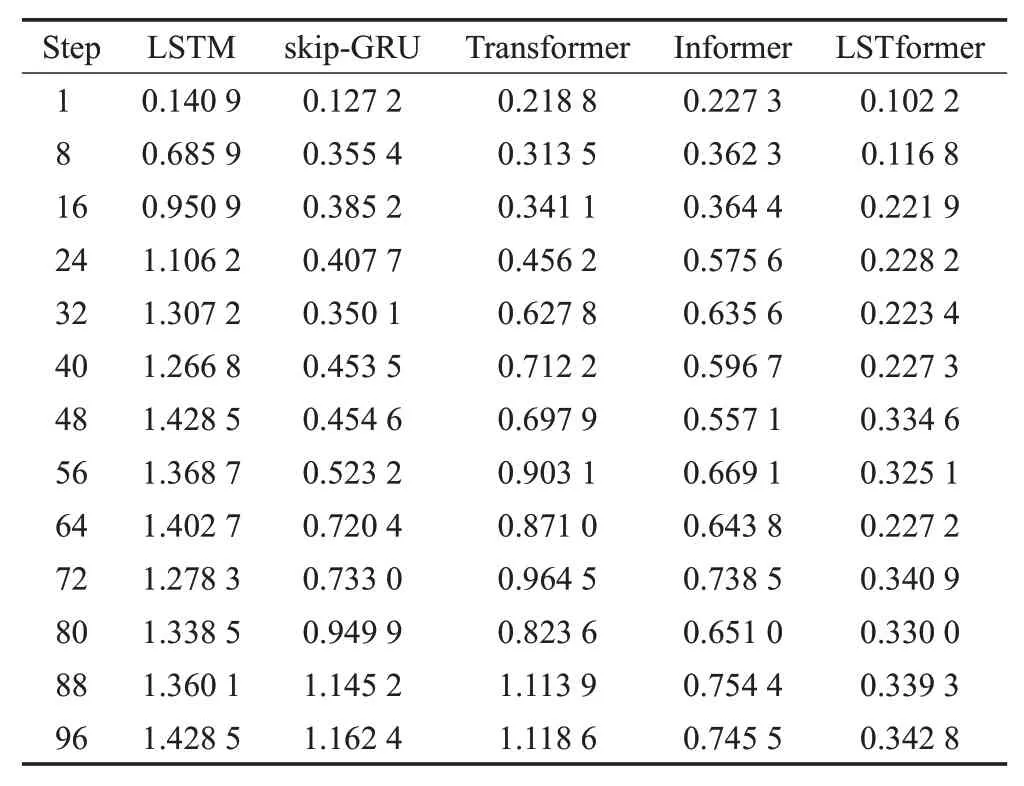
表4 各模型不同预测步数的预测性能Table 4 Results of different steps for each model

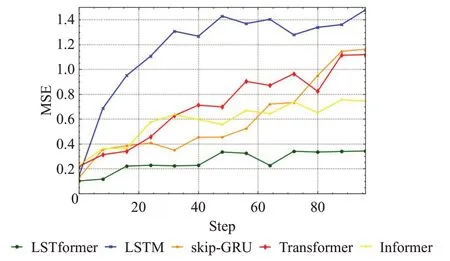
图8 各模型不同预测步数的预测性能Fig.8 Prediction performance of different prediction steps for each model

4.4.3 不同模型的预测性能讨论

根据表4 可知，LSTformer 在多步预测场景下表现优异，为了探究不同模型在24 h 的预测场景下的性能稳定性。本次实验中，依然选择LSTM、skip-GRU、Transformer、Informer 四个模型进行对比实验，除此之外，本文还对比了单独使用时序特征融合模块（即本文提出长、短时序特征选择模块用作预测模型的效果）的情况。在本次实验中，仅测试24 h（96个预测步数）场景下各模型的性能表现，进行10次实验结果取平均值，最终测试集预测结果如表5所示。

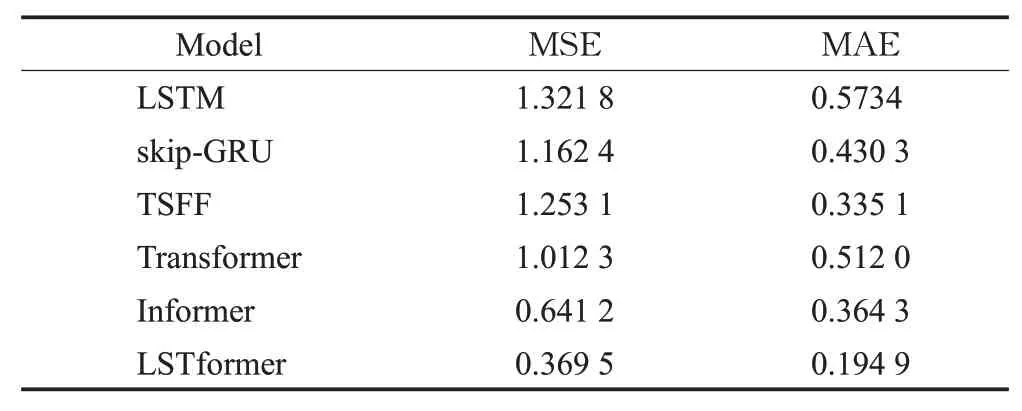
表5 24小时预测结果Table 5 24-hour prediction results

由表5可知：针对光伏发电功率预测场景，LSTformer模型与传统模型的性能指标对比，在24 h 预测场景（96预测步数）下，LSTformer 的MSE 分别降低了74.13%、68.21%、70.5%、63.49、50.43%，MAE分别降低了74.13%、54.70%、41.83%、61.93%、48.42%。

如图9 所示，本文将LSTformer 在测试数据集的预测结果进行反归一化，并将反归一化后的结果通过可视化操作展示出来，图中所展现的预测结果为7个24 h预测结果的集合，与真实数据对比偏差不大，可以看出LSTformer的精度较高，误差较小。

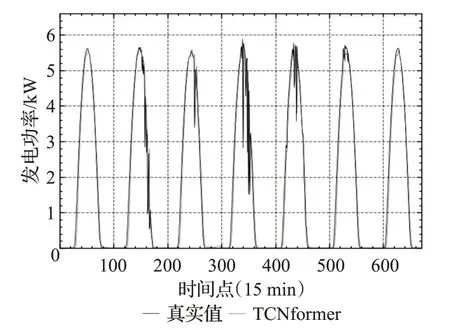
图9 LSTformer模型的预测结果Fig.9 Results of LSTformer model

4.4.4 消融实验

为了验证LSTformer模型各优化模块的有效性，进行了消融实验，将LSTformer模型中几个创新模块分别移除进行对比实验，即分别设置：

实验1去除时序分析模块。

实验2去除时序特征融合模块。

实验3去除Transformer结构，采用时序分析模块+时序特征融合模块+全连接网络。

实验4将时间卷积前馈单元替换为传统Transformer系列模型中的线性层FeedForward。

实验5完整LSTformer模型。

如表6所示，针对本文提出的几个创新模块：时序分析模块、时序特征融合模块、引入一步解码的Transformer模型结构、时间卷积前馈单元，不论去除哪个模块，都会导致模型的误差加大。当不采用一步解码的Transformer模型结构后，造成的误差最大，移除时序分析模块对LSTformer模型的MSE指标影响最小，但仍会造成精度的下降。移除时间卷积前馈单元对LSTformer 模型的MAE 指标影响最小，对MSE 指标的影响也仅比时序分析模块大一点，综合而言，移除时间卷积前馈单元对LSTformer 的影响最小，但是通过这些数据可以得出结论：本文提出的LSTformer 模型是有效的，每一个创新模块都是有意义的。

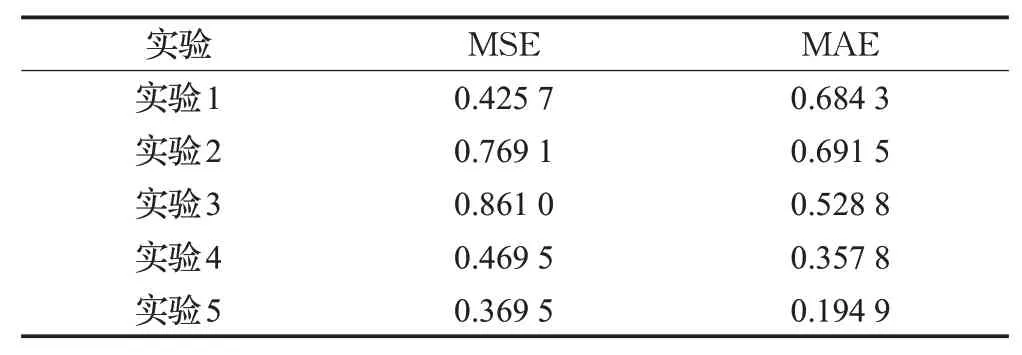
表6 消融实验结果Table 6 Results of ablation experiments

5 结束语

文中利用LSTformer 模型进行光伏发电功率短期预测。以澳洲某光伏电站实测数据为例，将该模型与单一模型实验效果对比，得出三点主要结论：（1）文中提出的LSTformer 光伏功率预测模型采用了Transformer 结构，结合了LSTnet、Informer等多个优秀模型的优点，且实验结果表明，该模型能有效提高短期光伏出力预测精度。（2）创新性地提出了设计时序分析模块、时序特征融合模块、时间卷积前馈单元，更充分地提取了多时间尺度的时序特征以及其他天气因素对光伏发电功率的影响。（3）LSTformer 模型与LSTM 模型和Transformer 系列模型相比，在多步预测上拥有更高的精度，但仍然还有优化的空间。在后续研究中，将针对LSTformer模型进行优化，使其具有更强的泛化性。