数据驱动的城市固废焚烧过程烟气含氧量预测控制
孙 剑,蒙 西,乔俊飞
(北京工业大学信息学部,北京 100124;智慧环保北京实验室,北京 100124;智能感知与自主控制教育部工程研究中心,北京 100124)
1 引言
近十年来,随着经济的快速发展和城市化进程的加快,城市固体废弃物(municipal solid waste,MSW)产生量呈逐年增加趋势,“固废围城”正成为许多城市面临的严峻挑战[1-2].城市固体废弃物焚烧(MSW incineration,MSWI)具有无害化、减量化和资源化等特点,是一种应用前景广阔的MSW处理技术.
在MSWI过程中,水平烟道出口处的烟气含氧量是与焚烧效率和污染物排放密切相关的重要参数.如果烟气含氧量过小,即过量空气系数过小,则表明不完全燃烧热损失增加,燃烧效率就会下降,还会产生大量的二噁英、一氧化碳和二氧化硫等有毒有害气体;如果烟气含氧量过大,即过量空气系数过大,则表明空气量送入过大,过量的空气会带走大量的热量和灰尘,也会增加燃料型NOx污染物排放.此外,固废焚烧过程内部发生着多种物理化学反应、传热传质和多相流体流动,同时伴有高温、高压和多相耦合作用.在传统工业燃烧过程控制中,在给料稳定时一般通过专家经验调节给风量控制烟气含氧量.但是,由于操作员的经验、专长与水平不同,烟气含氧量主观随意性较大,难以实现有效控制.此外,以比例-积分-微分(proportion integration differentiation,PID)控制为代表的无模型控制算法虽然实现简单,但鲁棒性差,难以实现烟气含氧量的精准控制.随着智能控制技术的应用发展[3-5],自抗扰控制[6]、线性二次调节控制[7]、神经网络控制[8]、模型预测控制[9]等方法也已成功应用于各种燃烧控制过程.其中,模型预测控制(model predictive control,MPC)作为处理约束优化问题的先进控制算法,具有一定的自适应性和鲁棒性,受到不少研究学者及工程技术人员的青睐.Leskens等人[10]针对典型的城市固废焚烧控制问题,率先建立了线型模型预测控制系统,使主蒸汽流量和烟气含氧量稳定在理想工作点附近.Huang等人[11]针对燃煤发电厂烟气含氧量跟踪控制问题,结合模糊C均值聚类和子空间辨识方法对模型参数进行辨识,提出一种模糊多模型预测控制策略,并通过实时控制仿真验证了控制方法的有效性.B¨ohler等人[12]开发了一种基于分级燃烧的生物质小规模燃烧模型预测控制器,实现了生物质燃烧过程烟气含氧量的稳定控制.这些方法一般需要先将机理模型转化为线性离散的状态空间方程形式,再进行线型模型预测控制器的设计.然而,对于城市固废焚烧过程这种具有强非线性特性的被控对象,线型化模型难以准确描述过程动态特性,从而导致预测控制器性能下降.因此,如何建立能够准确预测烟气含氧量动态变化的非线性系统模型是实现高品质控制的关键性问题.
机理建模和数据驱动建模是模型预测控制器设计中常用的两种建模方法.在构建机理模型过程中,通常要求具有足够多能够反映工况变化的过程参数,这在很大程度上依赖于科研和工程开发人员对实际工业过程的认识,并需要在苛刻的假设条件下才能成立.然而,MSWI过程是非线性且时变的复杂动态过程,内部发生着复杂的物理和化学反应,机理模型难以建立并实际应用于MSWI过程烟气含氧量控制.近年来,随着数据存储和信息技术的飞速提升,数据驱动技术的发展受到了极大的关注[13-16].许多快速轻量级的模型在工业过程中得到广泛应用,如扩展卡尔曼滤波、无迹卡尔曼滤波和滚动时域估计等.一般来说,这些方法需要假设噪声类型和模型结构,限制了其在实际工业过程中的使用[17].数据驱动的建模方法是基于过程采集数据建立的,不需要深入了解过程机理且算法通用性强.在众多数据驱动模型中,长短期记忆(long short-term memory,LSTM)网络是一种特殊的循环神经网络,可用内部存储单元上的门控机制来学习输入序列数据之间的长期依赖关系,对时间序列数据具有较好的预测性能[18].近年来,LSTM网络及其相关改进方法已成功应用于卷烟过程[19]、铅锌泡沫浮选过程[20]和燃煤发电过程[21]等工业流程关键指标建模.城市固废焚烧过程数据具有典型的时序特性,因此,选取LSTM网络用于建立该过程的烟气含氧量预测模型.
近年来,许多研究者致力于将LSTM 神经网络作为MPC非线性系统建模的重要工具之一.Ai等人[22]通过建立LSTM神经网络模型近似锑浮选过程,进而设计数据驱动的模型预测控制系统,实现给定参考值的跟踪控制.Chen等人[23]借助期望工作区域内的数据建立LSTM神经网络模型,并设计基于李雅普诺夫函数的分布式模型预测控制,在保证闭环状态有界和收敛到原点的同时,实现了高效的实时控制.Terzi等人[24]基于实验数据建立LSTM神经网络动态模型,并使用扩展卡尔曼滤波器作为状态估计器,构建了数据驱动的模型预测控制方法,并成功应用于大型商业中心冷却系统.上述方法多采用试凑法决定LSTM模型结构,然而该设计方式效率较低且模型泛化性能不强[25].确定合适的网络结构是LSTM神经网络模型构建的关键步骤之一,结构过小或过大都会导致神经网络的欠拟合或过拟合问题.优化神经网络结构也是近年来神经网络设计的研究热点之一,主要有结构搜索和增长剪枝两种方式.遗传算法(genetic algorithm,GA)[26]、粒子群优化(particle swarm optimization,PSO)算法[27]和蚁群算法(ant colony algorithm,ACO)[28]等进化计算方法,已成功用于搜索寻优LSTM网络结构.然而,这些方法会导致较高的计算成本,难以应用于实际烟气含氧量控制过程.增长剪枝的自组织结构设计方法能够提高神经网络的学习效率和泛化性能,目前已有多种针对径向基函数神经网络(radial basis function neural network,RBFNN)[29]、模糊神经网络(fuzzy neural network,FNN)[30]和深度信念网络(deep belief network,DBN)[31]等网络结构自组织设计方法.这些方法是通过预测精度变化或者神经元个体激活强度来设计自组织规则.然而,在实际烟气含氧量预测模型设计中,计算每次结构变化后的预测精度和确定合适的激活强度固定阈值是十分繁琐和困难的.此外,关于LSTM 神经网络自组织结构设计的文献还鲜有出现.因此,如何根据待处理任务有效地构建结构紧凑且预测性能优良的LSTM预测模型仍然是一项挑战性问题.
MPC设计的另一项难题是在有限时域内在线求解非凸优化问题[32].近年来,许多学者提出了不同的非凸优化方法.Li等人[33]对非线性模型进行线性化处理,采用简单的二次规划方法即可求解线性最优控制问题,避免了直接求解非凸优化难题.然而,对于一些强非线性系统直接采用线性化方法是不恰当的,这可能会恶化控制系统品质[34].粒子群算法、遗传算法和布谷鸟搜索等群智能优化算法也已被应用于求解预测控制律[35-37].但是,智能优化算法计算效率较低,难以实现实时控制.因此,不精确的模型线性化和长耗时的群优化计算很难满足MPC技术工程应用的实际需求.近年来,许多学者使用梯度下降方法来解决模型预测控制的优化问题[38-40].基于梯度下降方法的神经网络模型预测控制算法具有预测精度高和计算复杂度小的特点,非常适合用于求解MPC的实时优化问题.
针对MSWI过程烟气含氧量控制问题,文中提出一种数据驱动的城市固废焚烧过程烟气含氧量模型预测控制方法.首先,基于神经元影响值(neuron impact value,NIV)和显著性指标(significance index,SI),设计了单隐含层结构的自组织LSTM(self-organizing LSTM,SOLSTM)神经网络,隐含层神经元结构可以根据训练数据的变化而增长或修剪,在达到模型结构精简的同时提高模型泛化性能.其次,借助梯度下降算法滚动优化控制目标函数,在线求解控制律,提高求解效率.此外,基于李雅普诺夫稳定性理论分析控制系统的稳定性.最后,通过MSWI 厂实际数据验证了所提方法在烟气含氧量控制方面的有效性.
2 MSWI过程及模型预测控制
2.1 MSWI过程
在MSWI过程中,MSW通过干燥、热解、燃烧和熔融等过程,实现无害化处理、资源化利用和快速缩减体积的目的.文中的研究对象是某城市固废焚烧处理厂SN型阶梯式(倾斜+水平)顺推炉排焚烧炉,焚烧处理能力为800 t/天,主要由固废储运、燃烧炉、余热锅炉、蒸汽发电和烟气处理等系统组成.MSWI炉排炉工艺流程如图1所示.

图1 MSWI的工艺流程Fig.1 MSWI process flow
MSW由收集车运往城市固废处理厂后,被倒入固废池进行贮存.经过5~7天的充分混合和抓取发酵后,MSW成分更加均匀,渗滤液缓慢流入渣坑.然后将混合后的MSW推至液压驱动炉排,该炉排包括干燥炉排、燃烧炉排1段、燃烧炉排2段和燃烬炉排.助燃空气主要来自固废池,分为炉排下方的一次风和上方的二次风,既能供给焚烧又能有效防止恶臭逸出.在850~950℃的燃烧温度下,有毒有害物质能够被充分分解.此外,采用选择性非催化还原(selective non-catalytic reduction,SNCR)技术去除燃烧气体中的NOx,使其达到排放限值以下.排出气体主要包括氮氧化物、二噁英、碳氧化物、水、氧气和非焚烧残留物等酸性气体(如二氧化硫(SO2)、氯化氢(HCL)).酸性气体、有毒气体和重金属由石灰石和颗粒活性炭去除,以防止二次污染.最后,净化后的烟气经引风机从烟囱排出.
在实际焚烧过程中,需要充足的氧气参与焚烧炉内MSW的充分燃烧、脱硫过程的亚硫酸钙氧化反应和脱硝过程的氮氧化物还原反应等工艺过程,但过量的氧气会增加排烟损失、风机电耗和尾气处理规模.因此,将烟气含氧量控制在合理范围内,对于MSWI过程提高焚烧效率、降低污染物排放和增加经济效益具有重要意义.现场分布式控制系统(distributed control system,DCS)存储的历史数据蕴藏了大量的过程信息,有利于开发数据驱动的烟气含氧量预测控制方法.然而,MSWI过程烟气含氧量模型预测控制设计过程中依然存在两项主要挑战.
1)MPC的控制性能很大程度上依赖于其预测模型的准确性,而预测模型的结构设计对建立结构精简且预测性能优异的数据驱动预测模型至关重要.
2)根据数据驱动模型预测控制的特点开发出求解效率高且实时性好的优化算法是工程应用的迫切需求.
2.2 模型预测控制
MPC本质上是求解一系列有限时域的优化问题来实现设定点的跟踪控制[41].基于有限时域优化的MPC公式定义为
其中:yr,和Δt分别表示参考输出、预测输出和控制律变化量.Hp是预测时域,Hu是控制时域(Hu 一般来说,在建立非线性动态预测模型时,系统可由非线性自回归外生(nonlinear autoregressive exogenous,NARX)模型表示为 其中:u(t)和y(t)是系统的输入和输出,f(·)是未知预测模型,nu和ny是输入和输出的最大延迟. LSTM单元一般由遗忘门、输入门与输出门3个门以及候选单元状态组成[42],如图2所示. 图2 LSTM单元结构Fig.2 The structure of the LSTM unit LSTM神经网络通过门控结构实现单元状态和隐含状态的信息更新,具体运算公式如下: 经前向传播后,LSTM网络的预测输出计算为 其中wout为输出权值.神经网络训练过程的损失函数定义为 其中yd(t)和yp(t)表示期望输出和预测输出.这里,权重和偏差通过时间反向传播(backpropagation through time,BPTT)算法进行更新[43]. 文献[44]提出,皮层网络通过一系列影响其突触和神经元特性的可塑性机制表现出惊人的学习和适应能力.这些机制允许大脑皮层的递归网络学习复杂时空刺激的表征.受这种可塑性原理的启发,文中提出一种基于神经元影响值和显著性指标的SOLSTM算法,实现隐含层神经元的动态优化,构造出结构紧凑且泛化性能好的网络.首先,根据NIV 评估隐含层神经元的活跃度,将活跃度较低的隐含层神经元进行修剪,以简化LSTM神经网络结构.然后,利用SI值评判神经元的显著性,对网络结构进行增长.即SI值作为隐含层和输出之间连通性的度量,较大的SI值所对应的神经元将被重新激活,以弥补过度剪枝可能造成的影响.SOLSTM神经网络的结构增长剪枝过程详细描述如下. 将输入变量按照一定比例进行增减变化后再次输入到模型,观察神经元输出的变化,并使用神经元活跃度评价指标NIV评估神经元对输入变化的响应.具体计算过程如下: 1)初始化网络模型结构,将输入变量pj按照比例α依次增加和减少,得到两个新的输入变量pj1和pj2,即 2)将新得到的输入变量pj1和pj2分别通过网络模型,得到两组新的神经元输出Aj1和Aj2,二者差的绝对值即为神经元对输入变量按α比例增减后产生的响应变化,记为NIVj,即 3)由于神经元影响值是神经元活跃度的具体体现,因此需要保留具有较大NIV值的神经元.这里,设定前m个神经元的累积NIV活跃度为γ,定义为 其中m是初始隐含层神经元个数.通过设置累NIV活跃度阈值ξ,保留最活跃的前Φ比例神经元且累积NIV活跃率γ高于ξ的神经元. 4)抑制剩余对输入变量变化不敏感的神经元,即将它们的神经元连接权值掩码MASK置0. 与大多数神经网络一样,LSTM网络的输出层起到求和的作用.如果输出权值的绝对值很大,则说明该权值所连接的隐含层神经元对网络总输出的贡献也较大.为了改善神经元过度修剪的情况,可以重新激活这些隐含层神经元.因此,提出基于输出权重的显著性指标SI来评价每个隐含层神经元的贡献. 若SI值越大,则说明对应的隐含层神经元对输出的贡献越显著.因此,根据每个LSTM神经元的贡献显著性,找出并激活最显著的前β比例神经元,即将它们的连接权值掩码MASK置1. MPC的控制性能与预测模型精度有着密切关系,DCS系统积累的历史数据可被用于建立模拟过程动态的数据驱动预测模型.在模型训练过程中,采用基于NIV和SI指标的增长剪枝策略,构建SOLSTM神经网络预测模型.此外,MPC的每个控制瞬间都需要求解在线优化问题,以获得最优控制序列.简单有效的非线性优化方式是十分必要的.这里,将烟气含氧量参考值跟踪问题转化为最小化控制目标函数的优化问题,并采用在线梯度下降法求解控制律.基于SOLSTM网络的MSWI过程烟气含氧量模型预测控制(SOLSTM neural network based MPC,SOLSTM-MPC)方案如图3所示. 图3 MSWI 过程烟气含氧量SOLSTM-MPC方案Fig.3 SOLSTM-MPC strategy of oxygen content in fue gas for MSWI process 参考轨迹以一阶平滑滤波的形式设置,使系统输出平滑地转移到参考设定点[45],即 其中:αr为调整因子,0<αr<1;ysp(t)是参考设定点. 由于系统扰动或模型失配等原因,预测模型输出ysp(t)与系统实际输出yd(t)之间存在偏差是不可避免的.一般使用上一时刻的预测误差err(t-1)进行反馈补偿[46].通过反馈补偿,可以提高预测模型精度.反馈补偿的具体公式如下: 滚动优化的基本思想是随着预测时域的平移反复地在线优化目标函数,求解一系列最优控制动作,把MPC的有限时域优化问题向无限时域的最优控制问题靠拢.目标函数由以下向量重新定义: ρ1和ρ2是控制权重因子.为了最小化(t),使用如下简便的梯度下降方法更新控制输入序列u(t): 其中:n=1,2,···,Hp,m=1,2,···,Hu.由文献[47]可知,上式可以简化为 对于LSTM网络来说, 文献[48]提出,当控制时域Hu为1时,可以克服求解优化问题时需要进行较大矩阵运算的问题,并取得令人满意的控制效果.因此,本文设置Hu=1,则式(24)可表示为 通过选取适当的权值ρ1,ρ2与梯度下降的学习率η,给出了SOLSTM-MPC收敛的充分条件. 定理1将µ定义为SOLSTM-MPC优化过程的参数,如式(32)所示,如果其满足下式条件,则该过程就是稳定的. 其中λmax是g(t)gT(t)的最大特征值. 证定义如下的李雅普诺夫函数: 其中E(t)=r(t)-(t).则李雅普诺夫函数L的差分形式为 易知,E(t)的时间导数为 将式(37)代入式(36),可得 其中I是一个Hp阶的单位矩阵.证毕. 引理1定义矩阵函数(κI-A)X=0,其中A是Hp×Hp阶的对称矩阵,X是Hp×1阶的向量.则A的特征值可以表示为 利用式(38)和引理,根据式(34)设置最优参数µ可得ΔL(t)<0,即SOLSTM-MPC是收敛的. 控制系统的稳定性是其成功应用的重要因素.对SOLSTM-MPC的稳定性分析如下. 定理2若烟气含氧量可由所提出的SOLSTM神经网络近似,且采用梯度下降方法求解控制律,则提出的SOLSTM-MPC方案的渐近稳定性可以得到保证. 证证明过程由两部分组成: 1)滚动优化目标(t)是递归可行的;2)SOLSTM-MPC是渐进稳定的. 1)设最优控制律在t时刻的变化量为 则t时刻的最优控制序列和最优输出序列为 在t+1时刻,设控制变量增量的可行序列为 则t+1时刻的可行控制序列和可行输出变量序列为 因此,滚动优化目标在t+1时刻是可行的. 2)考虑t时刻引入最优控制序列u*(t)的代价函数为 其中ε*(t+i|t)=r(t+i|t)-(t+i|t)是跟踪误差.根据文献[49],如果预测时域Hp足够大,则可以满足下式: 因此,对于t+1的时刻可行控制序列uf(t+1),代价函数可定义为 根据式(19)的终端约束,即εf(t+1+Hp|t)=0,可得 此外,Δu*(t+1)是t+1时刻最优控制律增量,一定是比上述可行控制变量Δuf(t+1)更优的解.因此,(t+1)≤(t+1)≤(t).该方案的稳定性得证.证毕. 为了验证所提方法在实际MSWI过程烟气含氧量控制过程中的有效性,文中基于某城市固废焚烧处理厂DCS系统存储的历史数据,对所提的建模和控制方法进行验证和分析.文中仅对给料速度和各阶段炉排速度调节量稳定时的一种典型工况进行建模和控制研究.选取干燥炉排下方的一次风流量(PAdry)和燃烧炉排1段下的一次流量(PAicnr1)两个可控变量和二次风流量(可测扰动)作为烟气含氧量预测模型建模的辅助变量.通过调节两个可控变量,实现可测干扰条件下的烟气含氧量变设定值控制. 文中使用的数据来自于现场DCS系统采集的1748组实测数据,采样间隔为2 s.选取前1224组数据(70%)作为训练样本,后524组数据(30%)作为测试样本,建立基于SOLSTM神经网络的离线预测模型.在进行控制之前,选择用于预测的模型输入和输出最大滞后量ny=nu=2. 设置SOLSTM网络的初始神经元个数为30,学习率η1=0.05,初始权值随机设置,采用BPTT算法对该网络进行训练.所设计的自组织机制预设参数大多是通过试错的方法来确定的.SOLSTM神经网络剪枝与增长机制的阈值thres1与thres2分别受参数Φ和β影响,对模型的结构与精度有着重要的影响.β=0.5时,不同Φ值下的均方根误差(root mean square error,RMSE)与隐含层神经元个数如图4 所示,Φ=0.8 时,不同β值下的RMSE与隐含层神经元个数如图5所示.由图4可以看出,β=0.5时Φ取0.8具有相对低的RMSE和相对精简的网络结构.由图5可以看出,Φ=0.8时,β取0.5具有相对低的RMSE和合理的网络结构. 图4 β=0.5时,不同Φ值下的RMSE与隐含层神经元个数Fig.4 RMSE and the number of neurons in hidden layer under different Φ values when β=0.5 图5 Φ=0.8时,不同β值下的RMSE与隐含层神经元个数Fig.5 RMSE and the number of neurons in hidden layer under different β values when Φ=0.8 经过上述分析,结构自组织过程的参数Φ,α,ξ和β分别设置为50%,10%,98%和80%.SOLSTM网络神经元个数变化如图6所示. 图6 隐含层神经元个数变化Fig.6 Number of neurons in hidden layer 为了验证该网络模型的有效性,选取了径向基函数神经网络(RBF)、模糊神经网络(FNN)和LSTM神经网络进行实验对比.表1是不同烟气含氧量预测方法的参数设置.不同方法的具体预测曲线如图7所示,预测误差曲线如图8所示.可以看出,所提SOLSTM模型能够较好地拟合烟气含氧量的真实值曲线,具有较好的预测精度. 表1 不同预测方法的参数设置Table 1 Parameter setting of different prediction methods 图7 不同方法的预测结果Fig.7 Prediction results of different methods 图8 不同方法的预测误差Fig.8 Prediction error of different methods 为了进一步对比不同模型的烟气含氧量预测效果,采用均方根误差(RMSE),平均绝对百分比误差(mean absolute percentage error,MAPE)和平均绝对误差(mean absolute error,MAE)评估预测性能. 式中yd(t),yp(t)和Q分别为真实值、预测值和测试样本数.不同方法预测性能的比较如表2所示.与RBF和FNN相比,LSTM和SOLSTM神经网络的RMSE,MAPE 和MAE值较低,体现了LSTM 网络在解决该类预测问题上的优势.此外,经过增长剪枝过程,最终SOLSTM网络的神经元个数为10.与LSTM网络相比,结构更加紧凑.因此,SOLSTM网络更适合于模拟MSWI过程中烟气含氧量变化的动态特性,为后续模型预测控制方案的设计提供了精准的预测模型. 表2 不同方法预测性能的比较Table 2 Comparison of prediction performance with different methods 基于上述SOLSTM预测模型,采用在线梯度优化方法滚动优化控制目标函数,即可得到控制序列.在控制策略实施前,需要预先设置一些预测控制参数.设置预测时域Hp=5,控制时域Hu=1,参考轨迹调整因子αr为0.1,控制权重因子ρ1和ρ2为5和1,控制律的在线梯度优化学习率η2为0.01. 结合现场专家经验,烟气含氧量参考设定值应设置在5%~6.5%.为了测试所设计SOLSTM-MPC 的控制有效性,对比实验选取了采用RBF,FNN和LSTM神经网络作为预测模型的数据驱动MPC.不同神经网络模型预测控制方案的烟气含氧量跟踪控制效果如图9所示,相关跟踪误差如图10所示,相应控制量变化如图11-12所示.反馈校正误差补偿变化情况如图13所示.从图9-10可以看出,与其它方法相比,基于SOLSTM神经网络的预测控制方案能够更及时地给出准确的控制输出,使系统能够更快地跟踪烟气含氧量的变设定值.从图13可以看出,预测误差err(t)在控制起始阶段、设定值变化阶段的变化比较明显,说明这些阶段中的模型预测结果与实际值存在较大偏差.反馈校正对于减小预测误差,维持系统稳定起着重要的作用. 图9 不同方案的控制结果Fig.9 Control performance of different schemes 图10 不同方案的控制误差Fig.10 Control error of different schemes 图11 干燥炉排一次风流量变化(PAdry)Fig.11 Changes of the primary airflow under the drying grate(PAdry) 图12 燃烧炉排1段一次风流量变化(PAicnr1)Fig.12 Changes of primary airflow under the first incineration grate(PAicnr1) 图13 反馈校正误差补偿变化情况Fig.13 Changes of feedback correction error compensation 此外,采用绝对误差积分(integral of absolute error,IAE),绝对误差与时间乘积积分(integral time absolute error,ITAE)来评价控制效果,具体公式如下: 式中:K是样本总数,eoc代表烟气含氧量参考值与真实输出值之间的误差.表3 给出了不同算法的控制性能比较结果.实验结果表明,所提出的SOLSTMMPC方案具有较好的烟气含氧量变设定值跟踪性能. 表3 不同控制方案的控制性能比较Table 3 Comparison of control performance_with different control schemes 文中提出了一种数据驱动的MSWI过程烟气含氧量模型预测控制策略,基于实际工业数据的实验结果表明,在变设定值和可测干扰条件下,该策略具有较好的控制性能.SOLSTM神经网络模型能够动态地、自适应地调整隐含层神经元个数,得到精简的模型结构和较高的预测精度.相较于LSTM 网络,预测精度性能指标RMSE,MAPE 和MAE 分别降低了34.8%,36.7%和34.6%.此外,采用梯度下降法可以快速求解控制律,并基于李雅普诺夫理论证明了SOLSTMMPC 的稳定性.相较于其它神经网络预测控制方法,SOLSTM-MPC具有响应速度快和性能稳定等优点,可以获得较低的IAE 和ITAE,至少降低了55.1%和53.7%.后续将进一步考虑固废燃烧效率和污染物排放等因素,实现城市固废焚烧过程烟气含氧量的实时优化控制.3 自组织LSTM神经网络
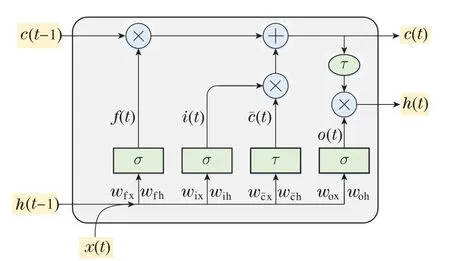
3.1 结构剪枝算法
3.2 结构增长算法
4 烟气含氧量模型预测控制
4.1 烟气含氧量预测控制器设计
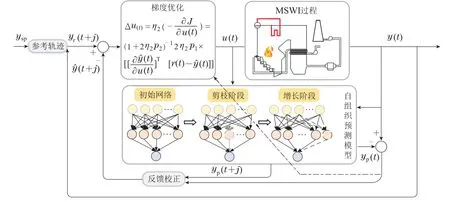
4.2 控制律梯度下降优化
4.3 收敛性分析
4.4 稳定性分析
5 实验分析与结果
5.1 SOLSTM预测性能

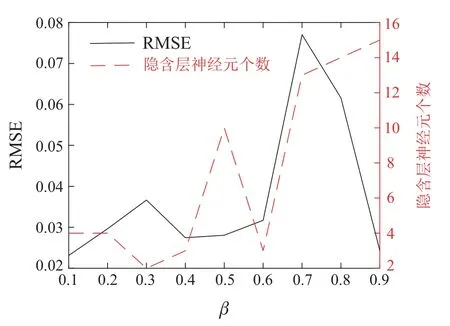
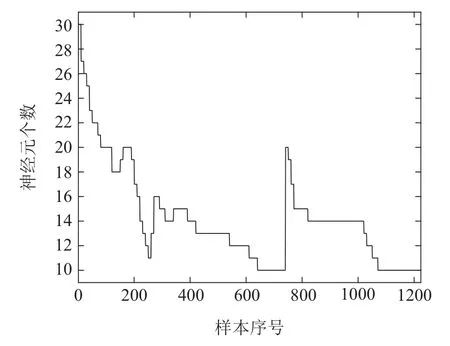


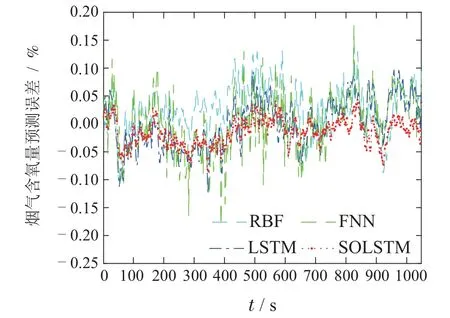

5.2 SOLSTM-MPC控制性能
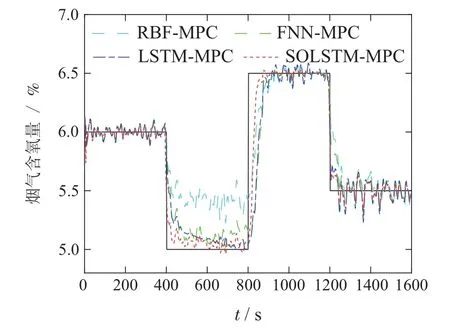





6 结论

