基于改进SFS算法的锚杆钻臂参数整定研究

陶 磊，陈 岳，王宏伟，李 超，姚林虎

(1.太原理工大学 机械与运载工程学院，山西 太原 030024；2.太原理工大学 山西省煤矿智能装备工程研究中心，山西 太原 030024)

“采掘失衡”是当今大型煤矿巷面临的难题，研发煤矿巷道智能支护设备对于解决此类问题，提高煤矿生产效率有着重要意义[1，2]。其中，锚杆钻臂自动定位控制是实现井下自动支护作业的关键，利用锚杆钻臂运送其顶端的自动钻锚机构准确的到达指定锚护位置。相对于传统机械臂自动控制技术，锚杆钻臂在煤矿井下巷道内工作，存在较强的干扰，以及环境不确定性，使得其他行业内的机器人控制技术难以直接应用于煤矿智能机器人控制[3]。因此推进高精度井下锚杆支护机器人智能化控制对加快我国实现井下锚护智能化以及智慧矿山建设有着极为重要的意义。

PID控制因其简单、控制效果好等优点[4]被广泛应用于各种设备的控制中，现将PID控制算法应用于锚杆钻臂控制中。由于井下工作的特殊工况，需要着重考虑PID参数的选择，传统PID参数整定过程采用配凑等方法，不仅耗时长，而且最终PID的控制效果不佳[5，6]。针对PID参数整定存在的困难，大量学者寻找其他方式优化PID参数[7-10]。EMRE Çelik[11]将随机分形搜索算法应用于自动稳压系统的PID控制中，优化了PID增益参数，得出利用随机分形搜索算法整定的PID参数具有较好的鲁棒性。Rahman T A Z[12]等提出4种混沌增强变体，提高了前代算法的收敛速度和搜索结果的准确性。VAN Tran H[13]等提出一种围绕所有现有解决方案探索大区域的方法对扩散过程进行改进，提高了搜索精度。学者们对随机分形搜索算法进行了大量的研究，提高了随机分形搜索算法的搜索精度，但针对复杂参数整定，算法陷入局部最优解、局部搜索能力不足的问题依然需要进一步突破。

综上，专家对随机分形搜索算法整定PID参数的方法及其改进进行了探讨，但针对井下锚杆钻臂控制器参数整定还需要进一步研究。本文针对自主研发的锚杆钻臂进行运动学分析，利用PID搭建各个关节的控制器实现锚杆钻臂自动控制，并对6自由度锚杆钻臂独立关节PID控制参数进行整定。针对整定参数多且存在大量耦合的复杂情况，对随机分形搜索算法进行改进处理。利用混沌初始化较好的随机特性提高初始化性能、融合正余弦策略的震荡变化特性提高局部搜索能力、采用不同变异策略跳出局部最优解。最后利用改进后的随机分析搜索算法整定锚杆钻臂PID控制参数，提高锚杆钻臂的运动控制效果。

1 锚杆钻臂结构分析

1.1 机械臂机械结构

为满足巷道支护智能化需求，实现井下巷道快速支护及保障井下工作人员安全，需要设计并实现智能化巷道支护设备，为此根据实际需求设计了钻锚一体式锚杆钻臂。该机械臂通过底座连接到锚护机器人本体上，由液压系统提供动力输入，锚杆钻臂姿态通过回转运动、大臂伸缩油缸、变幅油缸等液压执行元件配合实现，锚杆钻臂结构如图1所示。

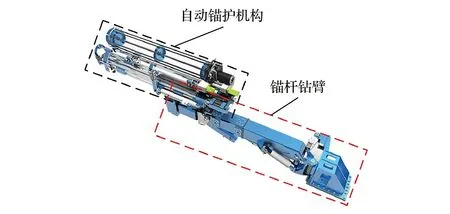
图1 锚杆钻臂结构Fig.1 Drill boom structure of the bolt

1.2 锚杆钻臂运动学分析

通过锚杆钻臂的正逆运动学对机械臂关节空间、操作空间的相互映射关系进行分析计算[14]。首先，利用D-H法求取锚杆钻臂的D-H参数以及齐次坐标变换矩阵，D-H参数见表1。

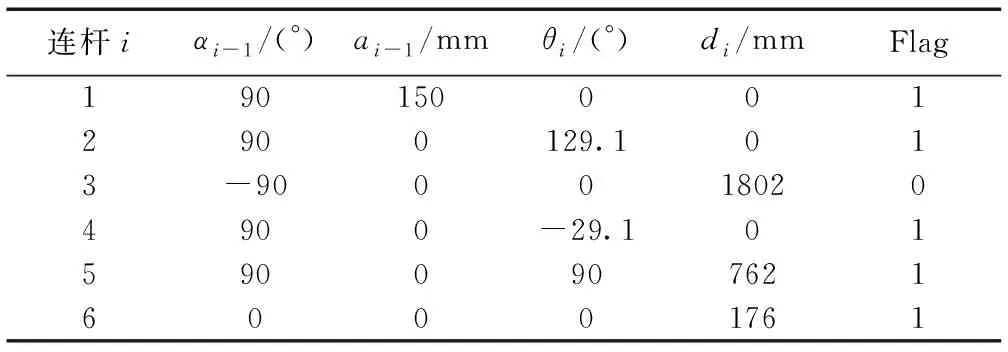
表1 D-H参数表Table 1 D-H parameters list

机械臂齐次变换矩阵见式(1)，带入D-H参数到式(1)可求出齐次坐标变换矩阵。

式中，i-1Ti为齐次变换矩阵。

完成坐标齐次变化矩阵求解后，可利用代数法求取机械臂各关节的逆解，可求解得出各关节所需的运动变量，求解出的关节逆解将赋予控制器进行控制[15]。

2 随机分形搜索算法及其改进

2.1 SFS算法介绍

随机分形搜索算法(SFS)是伊朗德黑兰大学学者Hamid Salimi于2015年提出的一种元启发式算法[16]。SFS算法是基于物质分形增长的特性创造的搜索算法，主要包括扩散过程和更新过程。扩散过程：采用高斯游走、布朗运动等方式对个体进行扩散处理，且最终保存唯一最优个体。扩散过程不仅能够增加寻找到全局最优解的几率，也能限制个体数量的急剧增长。两种高斯游走过程如式(2)(3) 所示。

GW1=Gaussian(μBP，σ)+(ε×BP-ε′×Pi)

(2)

GW2=Gaussian(μP，σ)

(3)

式中，ε与ε′为服从U(0，1)的变量；BP与Pi分别为在种群中最佳个体与第i个个体的位置；式(2)中μBP=|BP|；式(3)中μp=|Pi|。式(2)与式(3)中标准差σ=|log(g)/g×(Pi-BP)|。其中高斯游走的步长随着迭代次数g的改变不断改变，实现自适应步长，提高SFS算法的寻优能力。完成扩散过程并利用适应度函数求解个体的适应度函数值后，通过公式Pai=rank(Pi/N)对个体进行排名，并利用判断条件：Pai≤ε判断是否需要更新个体。若满足判断条件，则根据式(4)更新点Pi的第j个分量，若不满足条件，则保持不变。

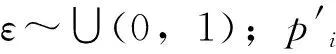
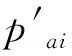
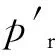
2.2 SFS算法改进

随机分形搜索算法具有较强的搜索能力，但是在后期在面对高维复杂问题时收敛速度慢、寻优精度不高，以及容易陷入局部最优解[17]。在对锚杆钻臂的控制参数进行寻优时，其参数间耦合严重、搜索空间较为复杂且具有较多的局部最优解。为了满足锚杆钻臂参数寻优整定的需求、解决随机分形搜索算法存在的问题，引入混沌初始化、正余弦策略、自适应选择策略、变异策略等操作，分别对初始化过程、扩散过程、更新过程进行优化改进，提高随机分形搜索算法的搜索性能，形成改进随机分形搜索算法NSFS。改进后随机分形搜索算法流程如图2所示。

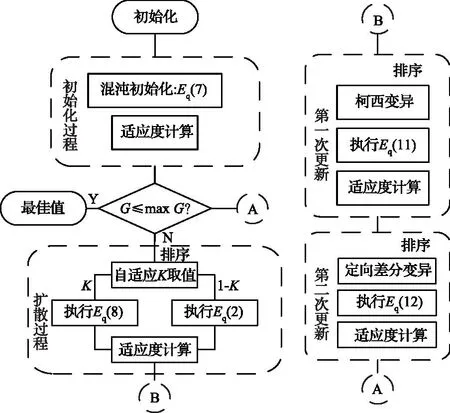
图2 改进随机分形搜索算法流程Fig.2 Flow chart of the improved random fractal search algorithm

1)初始化过程优化。智能算法的初始化过程在起始阶段起到关键的作用，它预先提供的先验知识，能够影响后续的搜索速度和质量。为了提高初始化的质量，采用混沌映射初始化种群。Piecewise混沌映射具有简单、随机性好的特点，将其运用到种群初始化中，能够提高初始化的效果。Piecewise混沌映射原理如式(7)所示。

式中，x(t+1)与x(t)分别为下一代生成的值与当代生成的值；p为(0，1/2)的变量。

2)扩散过程优化。随机分形搜索算法的扩散过程是该算法的核心过程，提高扩散过程的效率能够极大程度的提高随机分形搜索算法的搜索质量。采用高斯游走策略虽然有着较好的局部搜索能力，但是其搜索速度较慢以及依赖较大的采样数目限制了扩散过程的发挥。为了弥补其缺陷，现采用正余弦策略对扩散过程进行优化。正余弦策略利用正余弦函数具有的震荡变化特性，构造了能够实现全局搜索与局部搜素的迭代方程式[18]。在面对多耦合参数寻优时，利用正余弦策略能够提高算法的全局搜索能力及搜索效率。其原理见式(8)。

利用正余弦策略实现扩散过程经过多峰函数测试发现，正余弦策略前期具有较快的搜索速度，但是容易陷入“早熟”，局部搜索能力不足。为了进一步提高搜索能力，将正余弦策略与高斯游走策略进行综合选取，采用自适应K取值方式进行融合两种策略。K值能够随迭代次数进行自适应变化，K∈[0，1]。搜索前期通过取得较大的K值，以较大概率的方式选取正余弦算法实现扩散过程，以获取高效的全局搜索能力；后期则通过较大概率选取高斯游走方式提高局部搜索能力。

3)更新过程优化。为跳出局部最优，提高后期种群中物种多样性，将采用变概率变异策略与更新过程结合。首先引入柯西变异策略实现第一次更新过程[19]，其原理见式(11)。前期适应度较大时，采用较小的变异概率，当迭代到后期，适应度值变化程度小，种群多样性减少时，提高变异概率。

式中，m为0；b为1；u为区间[0，1]上服从均匀分布的随机数。

其次引入融差分定向变异策略的局部搜索实现第二次更新过程[20]，其原理见式(12)：

式中，r～U(0，1)，g为当前迭代次数，j、k为随机整数，ξ=0.9，θ=0.618；式(13)中，gamrnd()为伽马随机数。

2.3 改进算法测试

为验证改进后的随机分形搜索算法较原始搜索算法具有更强的寻优能力，将采用不同的测试函数对两种算法进行验证。采用的测试函数及其寻优结果见表2，寻优算法测试函数及收敛迭代如图3所示。

表2 测试函数及其寻优结果Table 2 Test functions and the optimization results

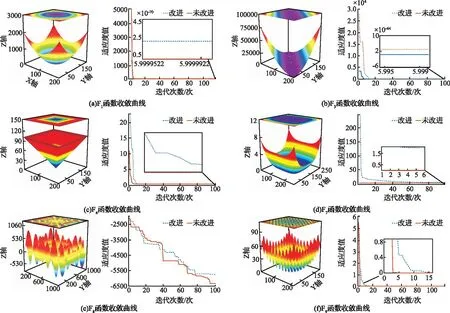
图3 寻优算法测试函数及收敛迭代Fig.3 Test functions and convergence iteration of the search algorithms

对比分析表2可知，改进后的SFS算法在测试函数F1至F8中最终迭代结果均优于原始SFS算法，对于F9测试函数，改进前后的SFS算法均达到最优解0；分析图3可知，改进后的SFS算法对于绝大部分测试函数寻优速度均快于原始SFS算法，对于F8测试函数，改进后的SFS算法，收敛平均速度快于原始SFS算法，且最终寻优结果更优。可以看出改进后的SFS算法在单峰、多峰测试函数的寻优速度以及寻优精度上均高于原始的SFS算法，因此可以认为，改进后的SFS算法具有更强的寻优能力。

3 SFS算法整定机械臂PID仿真分析

3.1 仿真环境搭建

锚杆钻臂是具有六个自由度的机械臂，其各个关节之间的耦合较为严重，求取精确的数学模型较为困难。因此使用Simscape对机械臂的系统模型进行模拟仿真，添加完成质量、关节副等内部参数，并利用Simulink模块搭建机械臂PID控制系统，对仿真机械臂进行控制。最后采用机械臂关节逆运动学求解赋予机械臂六个关节不同的运动变量。

为寻找合理的PID参数，实现机械臂抗干扰且具有较高精度的运动控制。采用SFS、正余弦SFS、混沌变异SFS、NSFS算法对PID控制器进行参数寻优，其原理如图4所示。Matlab通过函数调用Simulink模块，给定控制器阶跃信号，根据Simulink中模型各关节阶跃响应求取适应度值，反馈到Matlab中，通过不断循环迭代进行寻优。

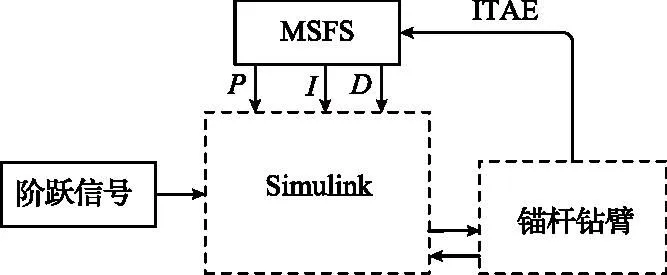
图4 随机分形搜索算法整定PID参数原理Fig.4 Principle diagram of PID parameters tuned by random fractal search algorithm

3.2 参数寻优

首先确定本次仿真的适应度函数，适应度函数见式(14)。

式中，tmax表示阶跃响应结束时间；e(t)为响应误差；t为当前时间。

其次，根据前期配凑法得出PID参数范围，设置寻优参数范围为[30000，100000000]。最后设置种群规模为15，迭代次数为30。分别利用原始SFS算法、改进后的SFS算法、正余弦SFS以及混沌变异SFS算法进行寻优。最终得到适应度值迭代如图5所示。

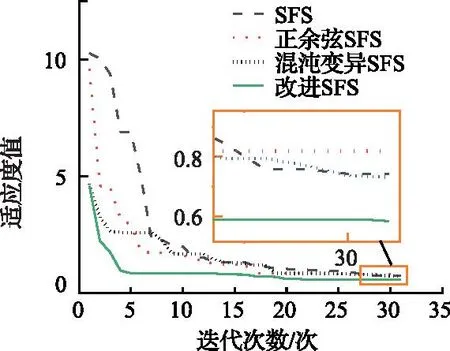
图5 基于改进SFS算法整定PID参数迭代Fig.5 PID parameter iteration adjusted by the improved SFS algorithm

从参数迭代图中可以看出，利用智能算法对锚杆钻臂控制器进行参数寻优，最终适应度值分别为0.74、0.82、0.73、0.58。可以分析得出改进后的随机分形搜索算法在四种智能算法中具有最强的搜索能力，较原始SFS算法搜索精度提高21%，且寻优速度更佳。

调用算法整定得出的关节PID参数到锚杆钻臂控制器中，求解锚杆钻臂各关节阶跃响应，其各关节阶跃响应曲线如图6所示。为便于评价，采用上升时间tr、超调量σ、调整时间ts对各关节阶跃响应曲线进行量化评价。但对于各关节在上升时间、超调量、调整时间上均各有优劣，较难评判其优劣。因此采用公式(15)对各个评价参数进行综合评价。

图6 锚杆钻臂各关节阶跃响应曲线Fig.6 Step response curve of each joint of the bolt drill boom

式中，w1、w2、w3分别为权重。现取w1、w2、w3分别为0.3、0.3、0.4计算各关节综合性能评价值，最终结果见表3。

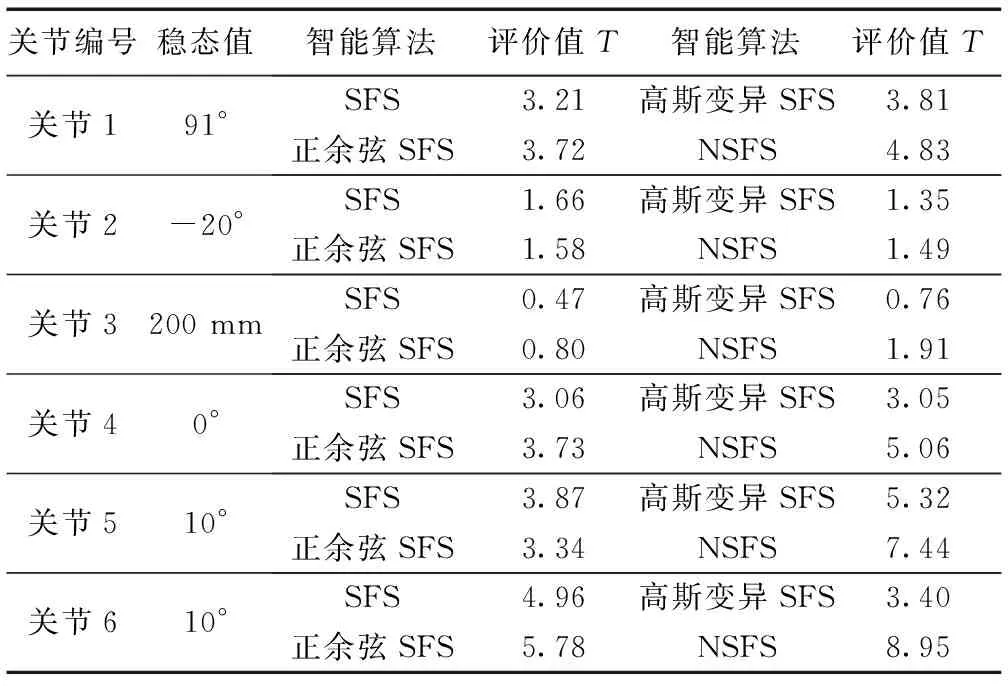
表3 锚杆钻臂各关节阶跃响应Table 3 Step response of each joint of the bolt drill boom

锚杆钻臂关节PID整定参数较多，且各关节之间存在大量耦合，利用智能算法整定的PID参数存在陷入局部最优的情况，即部分关节整定效果较好，其余关节效果不佳的情况。对比如表3可知，改进后的随机分搜索算法整定参数后的锚杆钻臂PID控制器阶跃响应除关节2的评价值T值略低，其余关节均优于其他算法整定的控制器；正余弦SFS仅关节3与5整定效果较好，但其余关节效果较差，算法陷入布局最优解；混沌变异SFS算法全局搜索能力较好，但最终的参数整定精度低于NSFS算法。

最终对比说明利用NSFS算法整定的锚杆钻臂控制器能够更好的跳出局部最优解，提高搜索速度，调整出更佳的控制参数，提高锚杆钻臂的控制效果。

4 结 论

针对随机分形搜索算法存在的搜索能力不足，面对高维复杂问题后期搜索速度慢、精度不足的问题，融合混沌初始化、正余弦策略、自适应K值策略、变异策略对搜索算法进行优化，利用标准测试函数进行对比得出改进后的随机分形搜索算法具有较高的搜索精度和速度；同时针对矿用锚杆钻臂存在的控制器调参数多难以调整且耦合严重的问题，应用改进前后随机分形搜索算法对其进行参数整定，对最终整定结果综合对比适应度值、各关节阶跃响应综合评价指标，发现改进后的随机分形搜索算法适应度值提高21%，关节评价指标除关节2略低于SFS、混沌变异SFS算法，其余关节评价指标T均高于其他算法。验证了改进后的随机分形搜索算法能够提高搜索速度与精度，同时能够跳出局部最优解，寻找各关节控制参数的全局最优值。