大概念驱动数学单元“问思辨”教学的实践与思考——以三年级下册第二单元“两位数乘两位数”教学为例

河北沧州市黄河路小学（061000） 邵英秀

河北沧州市新华区教师发展中心（061000） 王芙蓉

大概念是指学科知识体系之中的核心概念。大概念单元教学是以核心概念统摄单元目标，将零散知识通过概念联结，构建单元知识结构化的思想方法。两位数乘两位数笔算在小学“数与运算”教学中有着极其重要的作用。教师要引领学生在理解算理的基础上了解乘的顺序和积的书写位置，掌握算法，抽象出形式背后的本质——相同计数单位个数的累加，为进一步学习多位数乘法笔算奠定基础。

一、构建单元概念层级结构，使内容结构化

基于课程与教学中长期以来存在知识零散、碎片化和学生对内容缺乏深刻理解等问题，中外研究者从不同角度提出了大概念（或称大观念、核心概念）的观点，虽然视角各不相同，但总体方向、目标趋于一致，指向思想方法、核心目标、本质规律等的联结，更加突出知识的整体性、结构化。

数学大概念不是指向某一知识的具体概念，而是指向具体知识背后更为本质、更为核心的思想方法。大概念是指居于学科知识体系之中的核心概念，能把数学知识构建成一个连贯的整体。

（一）基于主题意义，聚焦本质提炼大概念

“两位数乘两位数”单元属于数与代数领域“数与运算”这一主题。“数与运算”的大主题学习时长跨越1~6 年级三个学段，数的类型涉及整数、小数、分数，因此运算法则有不同的表述，运算形式有横式、竖式。这些看起来零散且各不相同的知识点是否有本质的联系呢？支撑在内部的大概念是什么呢？去其表面，追根溯源。“位值制”是数学学科中可以统摄运算法则的大概念，它抽象概括了不同类型数运算的法则及各种运算法则背后统一遵循的规律：相同计数单位个数的累加。

（二）基于课程标准，依据教材确定概念结构

课程标准与学科教材是教师教学的重要依据与素材。分析课程标准对本知识的要求，以教材知识为载体，梳理提炼不同层次的大概念，是构建学科知识层级结构的另一维度。

“乘法运算”主题的内容要求包括：①能熟练地口算20 以内的表内乘除法，能口算简单的百以内的一位数乘除两位数。②能计算一位数乘两位数和三位数、两位数乘两位数的乘法。③经历与他人交流各自算法的过程。④能运用数及数的运算解决生活中的简单问题，并能对结果的实际意义做出解释。⑤能计算三位数乘两位数的乘法。⑥经历与他人交流各自算法的过程，并能表达自己的想法。

再来梳理教材关于“数与运算”的章节安排（见表1）。

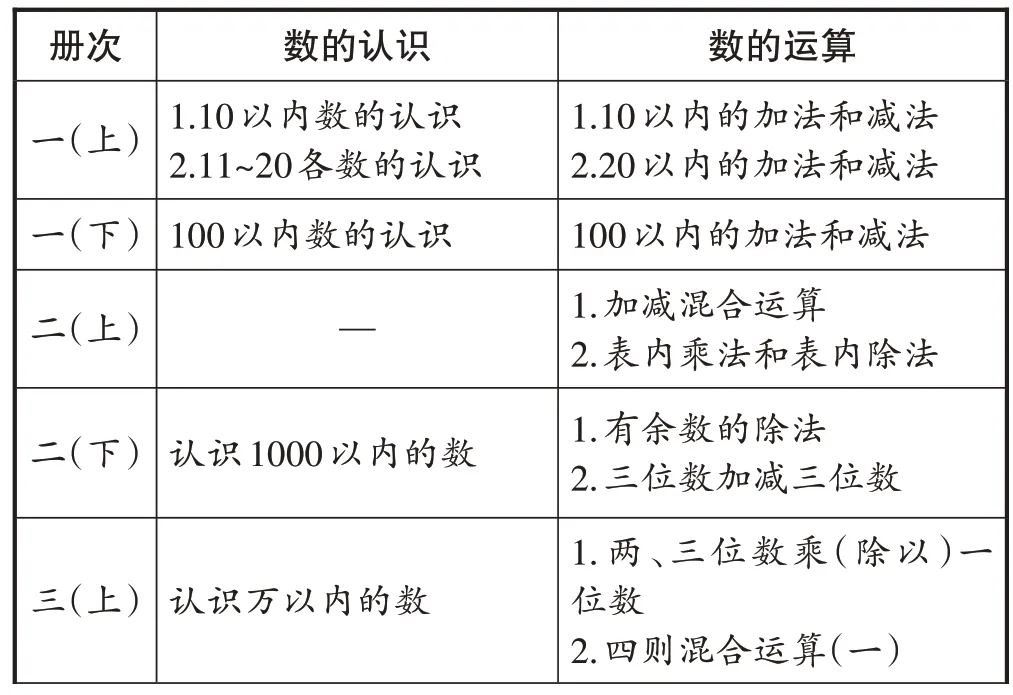
表1 “数与运算”内容分布

不难看出，数的认识与运算可以说是形影不离，那么数的认识与运算有怎样的关系呢？笔者高度认同马云鹏、吴正宪老师提出的“数认识是运算的基础，运算是数认识的再解读”的观点。

基于以上分析及思考，笔者对“两位数乘两位数”单元大概念进行提炼，构建了概念层级结构（如图1），形成了本单元内容的网状结构。

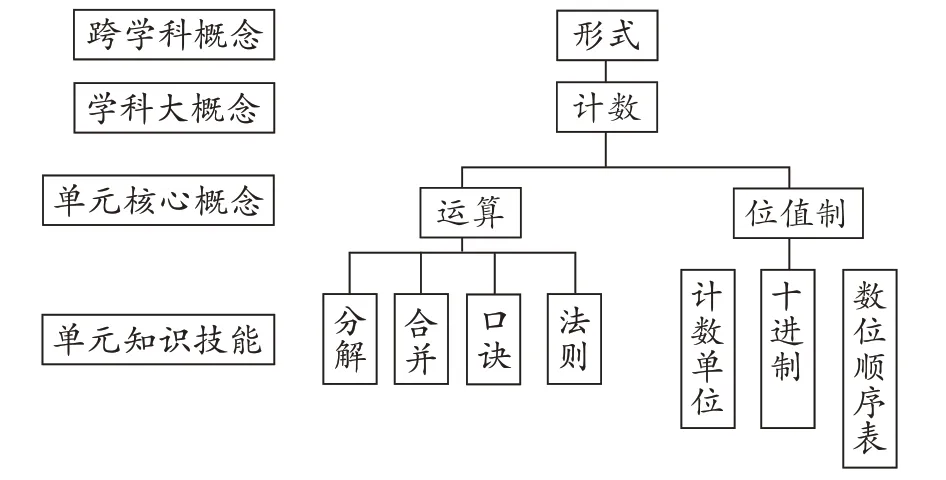
图1 “两位数乘两位数”单元概念的层级结构

二、依据内容结构化，进行单元重构

单元概念层次结构为教师把握核心内容起到了重要的支撑作用，为教学内容建立了由表及里的阶梯顺序。但仅仅有这样的概念层级结构还远远不够，教学时将抽象的概念巧妙植入学生熟悉的情境中进行儿童化处理，是从教师的教转化为学生的学的关键。首先，需要围绕核心概念对单元教学内容进行整体重构。笔者对三年级下册第二单元“两位数乘两位数”进行了单元重构（见表2-1、表2-2）。

表2-1 “两位数乘两位数”单元重构

这样的单元重构始终围绕笔算乘法形式背后的算理展开，增加了单元开启课和单元拓展课。在单元开启课“口诀遇上数位”上，学生围绕多位数乘一位数竖式用到的口诀和位置关系进行思考，明确由“口诀+数位意义”确定竖式。在最后的单元拓展课“竖式辩论会”上，将加、减、乘、除的竖式形式进行对比，找到其本质的关联。这样，学生就从点到面逐层加深了竖式形式背后统一的算理认识，从而将概念落实。单元重构中将两位数乘两位数笔算进位与不进位情况进行了课时合并，这样处理是考虑到两位数乘两位数竖式是笔算乘法的关键课时，其最不寻常的环节并非是否进位，而是把每次乘得的积进行分层记录，因此可以合并。同时在课堂巩固环节引入四年级下册两位数乘三位数笔算，这样学生才能真正感悟分层记录的本质，脱离机械模仿的状态。因此，将乘数末尾是零的竖式单独作为一个课时，是非常必要的。对于“乘数末尾的零不用乘直接写在积的后面”这一知识点，教学重点切勿停留在操作意义上，而是要揪出其背后的道理，从计数单位的意义层面理解直接写的意义，进一步落实位值制的概念，同时为进一步学习小数乘法奠定基础。笔者认为，估算的意义必须在实际问题中才有存在的价值，因此将其与解决实际问题进行了合并处理。

三、搭建“问思辨”课时框架，以大问题统领学习任务

“问思辨”是落实核心概念的儿童真实学习路径，以问题驱动思考发生，以问题追问辨析数学本质。下面以三年级下册第二单元“两位数乘两位数”为例，阐释搭建课时“问思辨”思维构想的意义（见表3）。

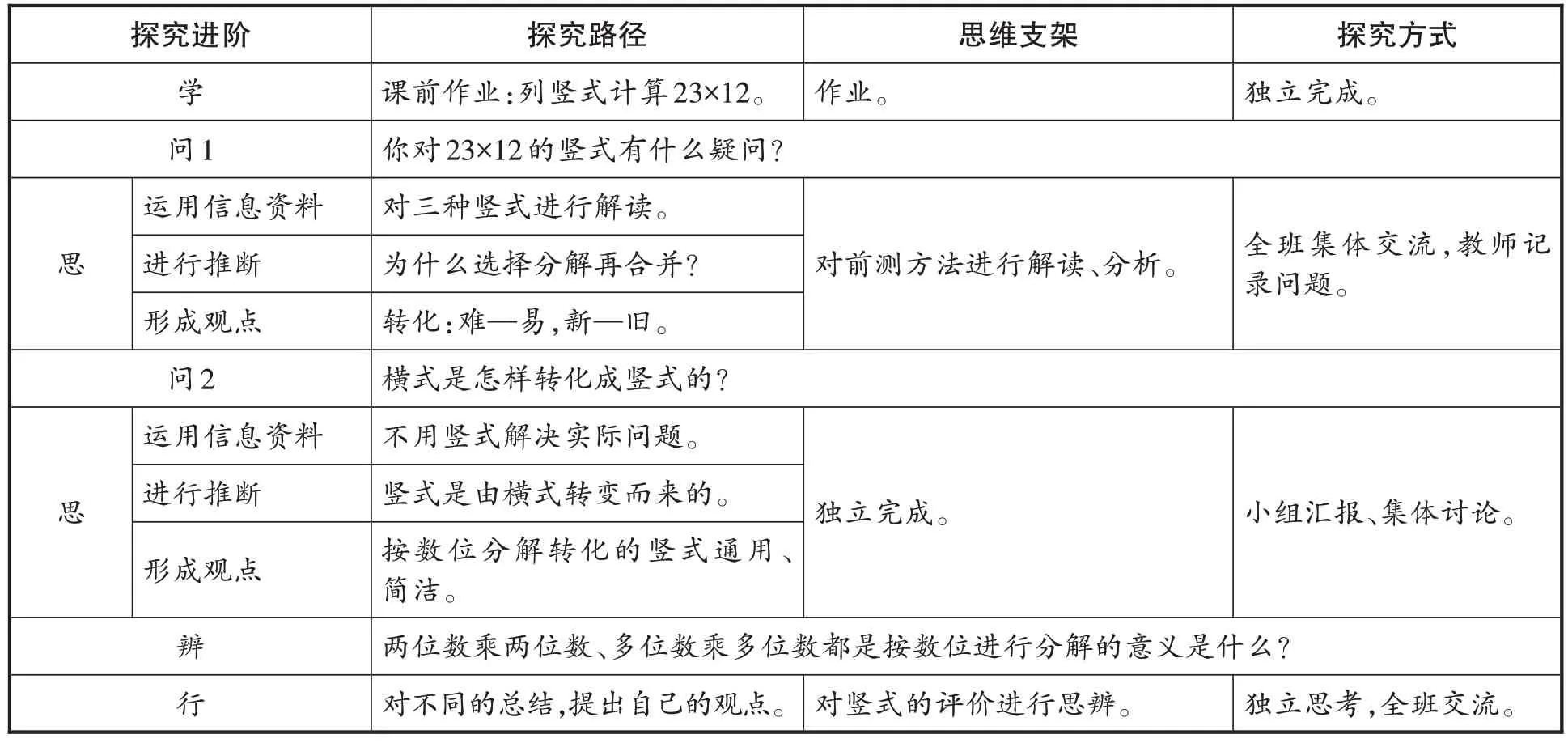
表3 “两位数乘两位数”问思辨概念教学课时构想

“问思辨”课时构想以结构化的形式展开，这节课似一幅画卷展现在学生面前，可以看出其中两个核心问题是“对23×12 的竖式有什么疑问？”“横式是怎样转化成竖式的？”，以此统领学生的学习任务，最后以问题“两位数乘两位数、多位数乘多位数都是按数位进行分解的意义是什么？”将学生的思考推向对竖式形式本质意义的归纳与拓展。整个过程超越知识技能的层面，伴随着思维的进阶提升。课时构想的“探究进阶”项给出了学生学习的方法“运用信息资料—进行推断—形成观点”，这不仅适用于现在的课堂，也是让学生一生受用的学习方法。课时构想中蕴含的独立思考、理性质疑、对比分析、归纳推理、交流分享等学习方式都指向学生核心素养的形成，体现数学课程育人的价值。

四、大概念驱动单元“问思辨”教学的思考

大概念驱动单元教学要求教师从更大范围、更深层次进行教学设计，通过结构化课程内容促进学生深层次理解知识的本质，使学生在“问思辨”中实现高阶思维的发展。

（一）大概念驱动“问思辨”单元教学，促进学生思维生长

数学学习的目的是激发学生思维的生长，而不是识记那些零零散散的知识或者熟练进行程式化运算。以往“两位数乘两位数”的教学常常是教师和学生一问一答把每一步乘的意义说出来，然后背法则，这样学生就只是记住了法则。而大概念“问思辨”单元教学以核心概念为准绳，通过几个核心问题引导学生思辨，让学生在不断思辨中认识到乘法竖式形式背后的大概念支撑，看到按数位分解的规律。课堂总结时，学生这样评价乘法竖式：“这个竖式真简单，以后不管几位数乘法都不怕了！”“竖式中光有口诀还不行，还要知道把积对齐数位，所以必须知道数的意义。”由此我们可以欣喜地看到，学生已经打破多位数乘法形式的壁垒，深入其本质意义，不再纠结程式化的第一步干什么、第二步干什么等。遇到连续进位的情况，学生还会用“替十法”灵活架构竖式形式，让问题变简单。经历本单元最后的拓展课“竖式辩论会”学习后，学生更加明确了加法、减法、乘法、除法的笔算竖式虽然形式各不相同，但都聚焦统一的核心概念，即“在相同单位上进行计算，是相同计数单位个数的累加（或细分）”。由此，学生的思维上升到形式是核心概念外显的认知层面。

大概念“问思辨”单元教学以核心概念统摄单元目标，将零散的知识通过概念进行联结，从表象深入到本质。学生在学习过程中跳出具体的知识来思考其背后的支撑，学习视野更开阔。知识镶嵌于概念层级结构中形成枝繁叶茂的知识树，以结构的力量实现思维的再生长。

（二）大概念驱动“问思辨”教学，促进教师以学科视角思考内容的本质及前后联系

单元大概念往往是比较抽象的，即使教师也是不容易看出的。它需要教师站在学科视角对教材或现实中提供的情境、材料进行抽象，深入解读课程标准定位概念，并对不同课时中的概念进行比对、关联，从而确定不同层级的概念，搭建层级结构，同时思考怎样将抽象的概念变成学生可操作、可思考的问题、任务。“问思辨”课时框架就是要将大概念充分对接学生认知水平设计核心问题，围绕核心问题设计任务，让学生在思辨、交流中理解概念本质。大概念驱动“问思辨”教学让教师从以往关注具体知识点的碎片化教学转变为关注课程的前后联系，实现教师自身的专业提升，促进学生的思维发展。

（三）“问思辨”课时建模是单元结构化教学落实的有效路径

单元结构化教学提炼出的核心概念对学生来说是抽象的，必须转化为学生学习可操作的思维抓手。在课时设计中以“问思辨”模型为思维支架开展学习，以核心问题统领学习任务。“两位数乘多位数”这一课时的核心问题为：多位数乘法竖式为什么是这样的形式？并围绕这个大问题出示三个小问题：（1）你对24×12 的竖式有哪些疑问？（2）横式是怎样转化成竖式的？（3）两位数乘两位数到多位数乘多位数，本质就是按数位分解意义的体现？这样可以有序展开教学，使学生在思辨、交流、实践中巩固知识技能，悟出其形式背后更为本质的学科思想和方法，形成核心素养。

大概念驱动单元“问思辨”教学的思考还有很多，广大教育工作者要在思考中前行，在前行中优化。