大数据系统与企业管理适配度评价指标权重确定研究

黄平根

江西理工大学商学院,江西 赣州 338000

0 引言

是否能够高度适配企业管理需求,是衡量大数据管理系统开发适用性和科学性的重要指标。目前,国内外关于大数据系统与企业管理适配度评价的研究较多,一些成熟的评价模型和算法也随之提出,但已有模型和算法的匹配指标权重仍主要依靠经验法确定,导致评价结果仍存在非线性、时变性和不稳定性问题。为提升大数据系统与企业管理适配度评价指标权重的精确度,本文引入消除非线性、时变性和不稳定性更优的“期望-熵”理论实施研究。

1 “期望-熵”理论概述

“期望-熵”理论由国内学者徐绪堪[1]提出,属于管理学和信息科学交叉领域理论,内涵为:信息系统与管理服务对象之间的适配度评价可用期望值(Ev)、熵(En)和外延熵(Ec)3个数字特征值表示,并通过期望值的浮动规律予以确定。其中,Ev是信息系统与管理服务对象最佳适配的中心值,也是衡量两者适配度的关键数值;En反映了信息系统与管理服务对象适配度的非线性和时变性干扰程度,数值在0.2～0.6时,两者的非线性和时变性干扰程度较低;Ec反映了信息系统与管理服务对象适配度的不稳定性程度,数值在0.05～0.1时,两者的不稳定性程度较低[2]。实际应用时,可通过专家选择、逆向发生器计算指标特征值、获取适配度权重值等步骤,确定信息系统与管理服务对象之间适配度的指标因素、权重等内容。

引入“期望-熵”理论确定大数据系统与企业管理适配度评价指标的权重,能够规避经验法确定指标权重存在的问题,通过Ev、En和Ec数据的加权呈现,得到期望值最优的评价指标权重数值,是大数据系统与企业管理适配度评价指标权重确定可探索和应用的最优方法之一。

2 大数据系统与企业管理适配度评价指标框架

在对已有研究文献进行梳理的基础上,本文创建了大数据系统与企业管理适配度评价指标框架,如表1所示。

表1 大数据系统与企业管理适配度评价指标

2.1 功能匹配度

用于衡量大数据系统开发的功能与企业管理需求之间的匹配度,具体通过功能是否完善及功能是否能够拓展2个二级指标进行测评。

2.2 架构匹配度

用于衡量大数据系统硬件和软件架构与企业管理应用之间的匹配度,具体通过数据架构应用是否适配及管理效果是否能得到显著提升2个二级指标进行测评。

2.3 战略匹配度

用于衡量大数据系统应用对企业管理战略达成辅助效应,具体通过数据系统应用后对企业管理战略达成效果的支持程度及表达性2个二级指标进行测评。

2.4 资源匹配度

用于衡量大数据系统开发配套资源与企业管理的适配度,具体通过数据系统开发现场环境是否优越、企业支持数据系统开发的政策是否到位2个二级指标进行测评。

3 大数据系统与企业管理适配度评价指标权重确定

3.1 权重等级范围设置

本文以“期望-熵”理论为依据,从期望值、熵值语言描述、强度等级、权重范围4个层面入手,编订了大数据系统与企业管理适配度评价指标权重等级范围描述表(见表2)。为了方便量化统计,为每个匹配指标分配“低、较低、一般、较高、高”5个语言描述等级。此外,根据语言描述等级,将权重强度等级范围也分为5个,等级越高说明该指标因素影响强度越强。例如:一级指标“功能匹配度”对应的二级指标“功能完善因子”的权重期望值,可在专家选择过程中从“低、较低、一般、较高、高”5个衡量等级中选取,选取结果也将被定量地映射到[0,1]区间,转换为具体的期望值,供逆向发生器计算指标特征值、获取适配度权重值等步骤参考应用。

表2 大数据系统与企业管理适配度评价指标权重等级范围描述表

3.2 专家选择

进行专家选择是运用“期望-熵”理论确定指标权重的首要步骤,通过专家选择能够确定权重初值,为后期的深度运算提供原始数据。

为了使专家选择确定的指标权重初值趋于科学合理,本文选择20位专家,其中包含5名大数据系统研发的教授级专家、6名高校企业管理专业教授、6名上市公司企业高管、3名大数据系统资深项目经理。以“功能完善因子”指标专家选择评价为例说明确定过程。①邀请专家结合自身对大数据系统、企业管理多年的开发实践经验,给出指标的熵值语言描述等级。②结合表2中的权重等级及范围,将专家定性评价语言转换为量化的权重范围数值,并用统计学方法进行整理,绘制出20位专家关于“功能完善因子”适配度评价权重的散点分布图(见图1)。③根据散点分布图,大致确定“功能完善因子”适配度评价权重数值范围。

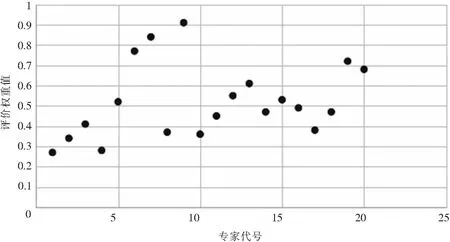
图1 专家选择给出的适配度评价指标权重散点图

3.3 逆向发生器计算指标特征值

通过专家选择获取“功能完善因子”指标的初步权重后,仍需要通过逆向发生器计算指标的特征值,以考证指标权重的Ev、En和Ec,通过这3个特征值的量化表现,综合判断指标权重的非线性、时变性和不稳定性干扰程度,以确保指标权重最优。具体来说,将“功能完善因子”指标专家选择确定的20个权重初值代入MATLAB[3]软件中,再运用软件中的逆向发生器算法进行计算,获得对应的指标权重特征值。具体程序代码如下。

Flag=0;

i=1;m=0;C1=C;D1=D;

While i<=(20-flag)

If D1(1,i)>0.99

D1(:,i)=[];C1(:,i)=[];

Flag=flag+1;

Else

I=i+1;

M=m+1;

End

End

Ex=mean(C1);En1=zeros(1,m);

For i=1:m

En1(1,i)=abs(C1(1,i))/sqrt(-3*log(D1(1,i)));

End

在MATLAB中新建工程项目[4],输入上述程序内容,导入20个专家选择确定的指标权重初值后,经过计算得到Ev为0.632 1、En为0.617 3、Ec为0.063 3。

3.4 获取适配度权重值

由逆向发生器计算结果可知,“功能完善因子”指标的En为0.617 3,不在En值认定的非线性、时变性干扰最优值0.2～0.6;Ec为0.063 3,在Ec认定的不稳定性干扰最优值0.05～0.1,说明得到的指标期望Ev为0.632 1仍有待优化。因此,进一步在MATLAB软件中运用逆向发生器过滤优化算法功能,对指标的特征值进行解析,获取优化后的3个特征值为:Ev为0.641 7,En为0.3557,Ec为0.072 1,符合“期望-熵”理论确定的特征值最优情况,得到“功能完善因子”指标的影响强度为五级[5],其权重为0.64。其他匹配指标的确定采用同样方法,最后得到完整的确定权重的大数据系统与企业管理适配度评价指标体系,如表3所示。

表3 确定权重的大数据系统与企业管理适配度评价指标体系

4 结束语

本文基于“期望-熵”理论确定大数据系统与企业管理适配度评价指标权重值,相较于以往的专家经验确定权重方法,本文采用的方法能够更好地考察指标权重的非线性、时变性和不稳定性,通过期望特征值描述评价指标权重的处理思路也更加科学合理,因此,最终确定出的评价指标权重体系也更为稳健,为企业成功建设和应用大数据管理系统提供了可靠保障。