用好思维导图，提升学生数学学习能力

■杨奇龙

思维导图是一种认知结构与思维图谱的体现，是在人脑发散性的基础上探索的一种结构，中央图形代表着主要焦点，从中央向四周发散，形成层次感较强的分支结构。思维导图在教学中的应用能够使学生形成知识结构体系，将抽象的知识形象化，在绘制思维导图的过程中查漏补缺，加深对所学内容的理解，提高知识迁移运用水平，从而提高教学学习能力。

一、利用思维导图，构建知识体系

在教学过程中，教师应利用思维导图带领学生整理知识点，梳理本章知识脉络，引导学生回忆已学知识，寻找相关主题，整合碎片化的知识点，清楚地展示各个概念之间的关系和层次，建立知识点间的联系，形成完整的知识体系。在绘制思维导图的过程中，不断巩固已学知识点，查漏补缺，加深对重要知识点的理解。

例如，在复习“圆”的相关知识点时，教师可以让学生先回顾本章的相关概念、定理等内容，让学生在回顾性质、位置关系等知识的基础上搭建知识框架，帮助学生在脑海重新建立“圆”的体系，便于后期解决问题时能够运用整体视角切入问题。同时，教师可以分小组绘制本章节的思维导图，让学生对本章知识点进行二次梳理。对于思维导图中缺失或者不足的部分，教师应及时指出或者补充，并且对遗忘的知识点重新巩固。完整的思维导图（如图1），不仅可以帮助学生直观地看出本章节的全部内容，还能进一步提高学生的理解能力。

图1

二、利用思维导图，引导学生深度思考

许多学生在做完题目之后，只在乎答案是否正确，并不在乎题目是否具有更深层次的意义，也没有进行深刻的自我反思，认为只要得到正确答案就万事大吉了，这样会导致数学学习能力停滞不前。为了帮助学生深刻理解问题，探究问题本身，教师应引导学生辩证地分析问题，利用思维导图，通过提出一系列探究性问题，让学生在问题串的引领下实现对问题的深入探究，发散学生思维。

例题 如图2 所示，以AB为直径的圆O分别与BC、AC交于点D、E，BD=CD，过点D作圆O的切线交边AC于点F。（1）求证：DF⊥AC；（2）若圆O的半径为5，∠CDF=30°，求BD的弧长（结果保留π）。

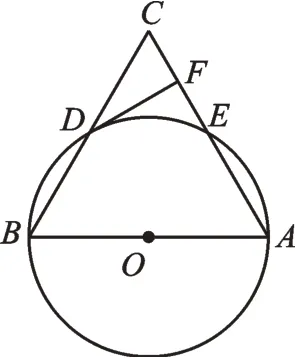
图2

在这道题的讲解中，教师可以让学生根据已知条件“D为切点”出发，连接OD，绘制初步的思维导图，然后根据已知条件，逐步向外发散，寻找未知条件，得到“OD为△ABC的中位线”，即能得到“OD//AC”，再根据“两直线平行，同旁内角互补”得到∠DFA=90°。第（1）问的难度不大，学生能够根据思维导图向外延伸，得到正确答案。第（2）问，教师可以通过提问的方式，让学生自主延伸思维导图，将已知信息的思维导图发展成完整的解题步骤。如，根据∠CDF=30°，你能得到哪些有用的角的度数？△ODB是什么三角形？弧长公式是什么？等等。同时，在解决完本题后，教师可以引导学生发散思维，积极思考，自主衍生第（3）问，“如果让你来出第（3）问，你打算从哪个方向提问，你又将如何解决？”通过这种方式，教师促使学生深入思考，不断前进，进一步掌握数学学习的本质。

三、利用思维导图，提高学生解题效率

在解题过程中，教师可以引导学生根据题目中的关键信息，利用关键词绘制思维导图，由关键词向外发散思维导图，挖掘与题目相关的知识点，寻找解决问题的突破点，利用思维导图呈现完整的解题思路，促进学生数学解题能力的提升。与此同时，教师还可以引导学生利用思维导图记录数学错题，如用“鱼骨状”“刺猬状”等形状的思维导图总结错题，在中心主题部分记录解题方法，末尾部分记录错题，中间部分记录产生错题的原因，使学生能够在解决问题的过程中明确错误的原因，提高学生的解题效率与正确率。利用思维导图记录错题，一是可以让学生自主归纳错题类型，将自己经常出错的题目放在一起，后续可以进行有针对性的复习巩固；二是可以将自己出错的原因整理归纳，看看不同的题目出错点是否重复或者交叉，从而从根本上避免这类情况的再发生。

例如，以错题本为基础，教师引导学生结合个人实际画出思维导图，根据学生的错题类型进行分类，如按照“计算错误”“概念错误”“应用错误”等分类，在此基础上分析做错的原因，是公式不熟悉、思路不清晰，还是理解偏差等，并将原因记录在思维导图的相应层级，最后制定纠错策略。

综上所述，在数学学习过程中，利用思维导图能够充分发挥数学教育功能，使学生串联数学知识点，呈现清晰的解题思路，提高学生解题的准确性。在此基础上，教师要加强对学生的引导，改善传统的教学模式，加强学生对思维导图的了解和应用，让学生能够利用思维导图不断探索数学问题的解决方法，提高学生数学学习能力，促进学生的全面发展。