高强钢筋超高性能混凝土框架结构易损性分析

贺少锋, 邓宗才, 李永梅

(北京工业大学 城市与工程安全减灾省部共建教育部重点实验室, 北京 100124)

超高性能混凝土(ultra-high performance concrete, UHPC)是一种通过添加活性粉末和增强、增韧纤维及优化骨料级配,制备出具有高强度、高韧性及良好的耐久性的水泥基复合材料。纤维的掺入可以延缓试件的开裂,改善试件的裂后工作能力,UHPC的抗裂应变为普通混凝土的7倍[1-2]。截止目前,国内外对UHPC的配合比、材料强度、韧性等方面进行了大量的研究。

在材料层面研究的基础上,学者们也对UHPC构件的力学性能展开了研究。配筋UHPC试件具有良好的延性,文献[3]研究表明在保证不发生纵筋屈曲及剪切破坏的前提下,UHPC结构可以大幅度减小横向钢筋的数量和间距。通过对配筋UHPC梁[4-6]、柱[7-11]进行抗弯、抗剪及抗震性能试验,总结了配筋UHPC构件弯曲、剪切破坏形态,给出了配筋UHPC构件变形、抗弯和抗剪承载力计算方法。此外,文献[12-14]还对约束UHPC的受压性能进行了研究,给出了约束UHPC受压承载力计算方法和约束UHPC本构模型。

然而,作为理论框架中的重要一环,目前对于高强钢筋UHPC结构地震易损性的研究尚属空白,且我国抗震规范[15]仅对普通钢筋混凝土结构的层间位移角限值进行了规定。而相较于普通混凝土构件,UHPC构件具有更好的延性和抵抗开裂的能力,如果以规范中弹性和弹塑性层间位移角限值进行地震风险预测及结构损伤评估,UHPC结构将失去其材料优势。

本文主要的创新点在于以高强钢筋和UHPC在结构中的组合应用为研究对象,在构件试验的基础上,运用增量动力分析(incremental dynamic analysis, IDA)方法,对比研究了普通钢筋混凝土框架结构和高强钢筋UHPC框架结构在不同地震动下的易损性,并利用配筋UHPC柱试验数据给出了适用于本文高强钢筋UHPC框架结构的层间位移角限值及建议性态点。

1 模型参数及材料本构

1.1 模型设计

模型为5层现浇混凝土框架结构办公楼,场地抗震设防烈度为8度(0.2g),地面粗糙度为B类,场地类别为Ⅱ类,设计地震分组为第3组,场地特征周期为Ts=0.75 s。屋面(含自重)恒载为4.96 kN/m2,屋面活荷载为0.5 kN/m2;楼面(含自重)恒载为3.3 kN/m2,房间活荷载为2.0 kN/m2,走廊活荷载为3.0 kN/m2。框架的首层高为3.3 m,上部结构层高均为3.0 m。在轴线上的主梁上设置墙体,内墙和外墙均采用混凝土空心砌块,容重取7.0 kN/m3。基本风压0.35 kN/m2。钢筋混凝土框架结构的阻尼比取0.05。钢筋混凝土容重取2.5 kN/m3。

为了对比研究普通钢筋混凝土结构和高强钢筋UHPC结构的抗震能力,以抗震规范条文为控制条件,选用名义屈服强度标准值不大于400 MPa的钢筋和C40混凝土对框架结构进行设计,根据设计结果在SAP2000中建立分析模型Frame-C;选用600 MPa级的高强钢筋和UHPC利用PKPM进行结构设计,根据设计结果在SAP2000中建立分析模型Frame-UHPC。结构的平面图和三维模型简见图1。

图1 框架结构计算简图Fig.1 Calculation diagram of frame structure

我国的抗震设计规范[15]地震水准需要考虑:小震(frequent earthquake, FE)、中震(moderate earthquake, ME)和大震(maximum considered earthquake, MCE)。其中中震的地震影响系数为小震的地震影响系数的2.8倍,由地震影响系数曲线及模型的自振周期计算得到小震、中震和大震所对应的谱加速度(Sa,FE、Sa,ME和Sa,MCE)如表1所示。

表1 自振周期及小震、中震和大震的谱加速度Table 1 Natural period and spectral acceleration of FE, ME and MCE

1.2 混凝土本构

1.2.1 C40混凝土

模型Frame-C所用混凝土等级为C40,取混凝土的弹性模量Ec为3.25×104MPa,峰值抗压强度fc,p为40 MPa,混凝土单轴抗压峰值应变εc,p为1.79×10-3。C40混凝土单轴受拉强度为3.5 MPa,峰值拉应变为1.28×10-4。受压和受拉本构方程参考《混凝土结构设计规范》[16]。

1.2.2 UHPC

1)UHPC受压本构。

邓宗才等[14]以UHPC单轴受压本构为基础,建立了高强钢筋约束UHPC轴心受压本构模型,曲线上升段和下降段表达式为:

(1)

(2)

2)UHPC受拉本构。

文献[18-19]在高韧性水泥基材料三线型模型的基础上建立了适用于UHPC的直线式的三线型模型,并利用有限元对模型的适用性验证。本文在以往研究基础上对UHPC的轴心抗拉应力-应变行为进行表征为:

y=kx, 0

(3)

(4)

(5)

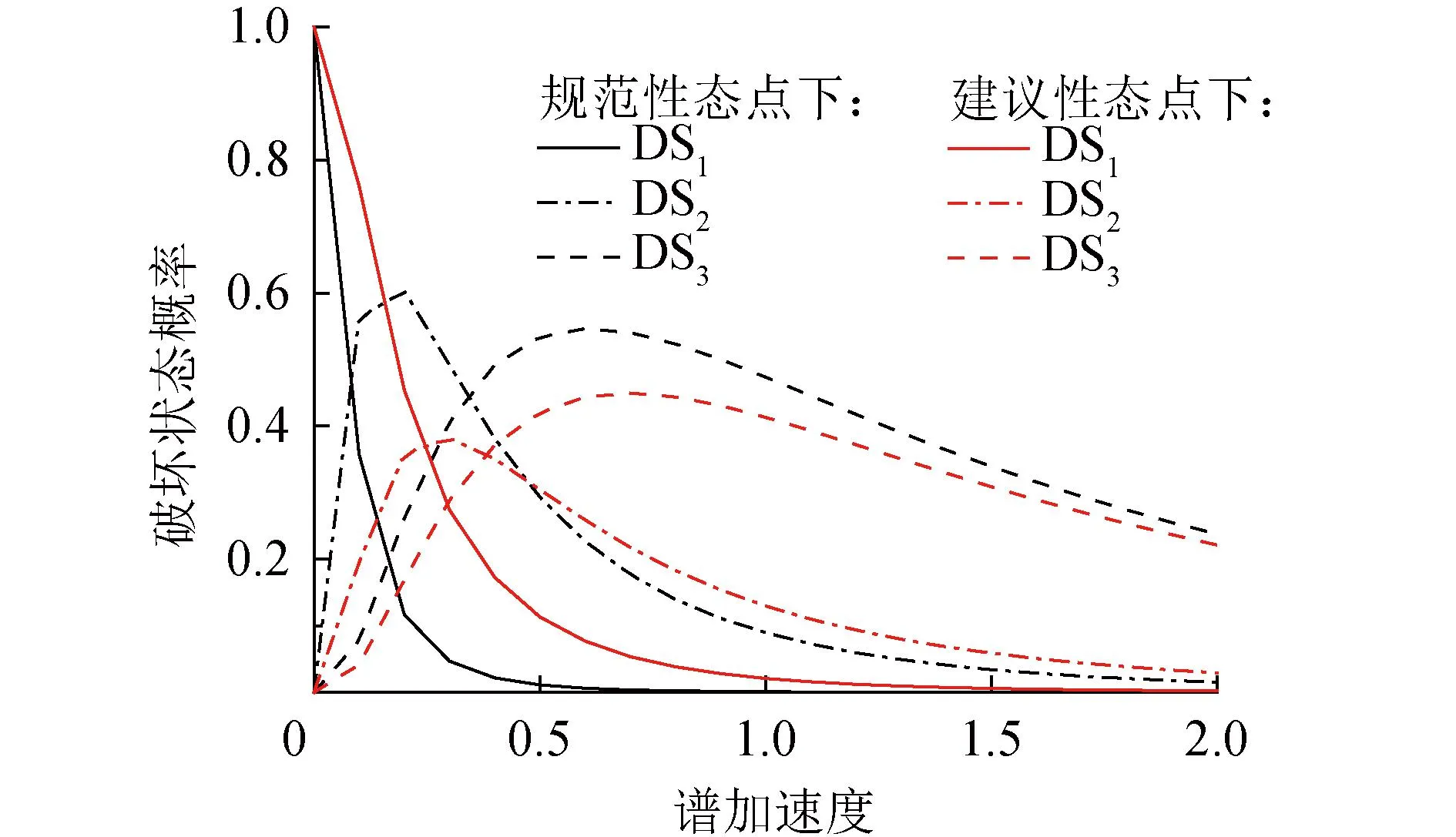
1.3 UHPC本构验证

为了验证UHPC的本构方程,利用有限元软件对文献[10]中的普通钢筋UHPC柱(试件编号LLC)和高强钢筋UHPC柱(试件编号HLC1、HLC2和HLC3)的试验结果进行了拟合,滞回曲线对比见图2,有限元、试验的最大荷载值(Pmax,FE、Pmax,test)如表2所示。

表2 有限元模型和试验柱的最大荷载对比Table 2 Comparison of peak load between finite element models and test columns

图2 试验试件和有限元模型的滞回曲线对比Fig.2 Comparison between the hysteresis curves of the test columns and the finite element models

可以看出有限元模型的滞回曲线与试验结果在加卸载刚度方面拟合良好,承载力衰减幅度与试验结果相近,可以较好反映试验试件的层间位移及延性。

2 概率地震需求分析

2.1 地震波的选取

从ATC-63[20]推荐的50条地震波中挑选震级超过6.5、地震动峰值加速度(peak ground acceleration, PGA)超过0.2g的地震动,其主要地震信息见表3。通过与抗震规范[15]中罕遇地震下的标准加速度反应谱对比(见图3),可知所选用的8条地震动与抗震规范中的标准反应谱误差在20%以内,拟合良好,所选地震动适用于该结构的时程分析。图3中g为重力加速度,取9.8 m/s2。

表3 地震动信息Table 3 Ground motion information

图3 加速度反应谱Fig.3 Response spectrum of ground motion records

2.2 概率地震需求模型

文献[21-22]指出结构需求参数和地震动强度参数一般服从指数回归关系,以谱加速度Sa为地震动强度参数:

(6)

对式(6)两边取对数得:

(7)

选取结构最大层间位移角θmax为结构需求参数,对所选的地震动样本逐一进行IDA分析,并利用式(7)对lnθmax～lnSa的散点图进行线性回归,得到模型Frame-C和模型Frame-UHPC的概率地震需求模型如图4所示。

图4 ln θmax～ln Sa的概率地震需求模型Fig.4 Probabilistic seismic demand model of ln θmax～ln Sa

3 基于规范的易损性分析

3.1 基于规范的地震易损性曲线

地震易损性曲线(极限状态概率曲线)作为结构易损性分析的一种形式,是以某一地震动参数为自变量,建筑物破坏概率为因变量的曲线。由该曲线可获得结构在给定Sa的条件下,结构地震需求达到指定破坏状态下的结构抗震能力参数的极限状态(limit states, LS)概率Pf(LS|Sa)。采用对数正态分布作为地震易损性的数学模型[23],则Pf(LS|Sa)表达式为:

(8)

把式(7)代入式(8)中,得:

(9)

式中:

(10)

根据抗震规范[15]规定,钢筋混凝土结构的弹性层间位移角和弹塑性层间位移角分别为1/550和1/50,据此定义轻微破坏LS1、中等破坏LS2、严重破坏LS3和倒塌LS4所对应的层间位移角中位值分别为:1/550、1/150、1/50和1/25。由式(9)计算4个极限状态的超越概率Pf(LSj|Sa)见图5。可以看出,结构的易损性曲线随着Sa的增加而单调增加。当地震动强度增加到某一范围后,易损性曲线逐渐平缓,结构达到某一极限状态的概率无限趋近于1.0。

图5 地震易损性曲线Fig.5 Seismic fragility curves

3.2 基于规范的破坏状态概率曲线

极限状态是指相邻2个破坏状态(damage state, DS)的界限,而破坏状态是指2个相邻极限状态的区间。我国抗震规范将建筑结构遭遇各种水准的地震影响时,其可能的损坏状况和继续使用的可能性,划分为5个破坏状态:基本完好DS1、轻微破坏DS2、中等破坏DS3、严重破坏DS4和倒塌DS5。根据Pf(LS|Sa),进一步计算可得到结构的破坏状态概率Pf(DS|Sa)为[26]:

P(DSj|Sa)=

(11)

式中N为极限状态个数。根据极限状态和破坏状态的关系,N个极限状态将结构划分为N+1个破坏状态。

根据图5和式(11)计算得Pf(DSj|Sa),见图6。可以看出,由于Pf(DSj|Sa)为结构处于某一震害区间的概率,故Pf(DSj|Sa)并不随Sa的增强而单调变化。对于DS2、DS3、DS4、DS5,当Sa为某一定值时,结构达到Pf(DSj|Sa)max,而后Pf(DSj|Sa)随Sa的增强而减小。

图6 破坏状态概率曲线Fig.6 Damage state probability curves

破坏状态DS2、DS3、DS4下,Pf(DSj|Sa)max所对应的Sa如表4所示。可以看出,当达到Pf(DS2|Sa)max时,模型Frame-C和模型Frame-UHPC的地震动强度均为0.2g,而当达到Pf(DS3|Sa)max和Pf(DS4|Sa)max时,模型Frame-UHPC达到的地震动强度均明显大于模型Frame-C,可见模型Frame-UHPC的抗震能力要优于模型Frame-C。

表4 Pf(DS|Sa)max所对应的谱加速度SaTable 4 Spectral acceleration Sa corresponding to Pf(DS|Sa)max

3.3 基于规范的结构损伤评估

根据Pf(DS|Sa),文献[27]定义结构的易损性指数(vulnerability index, VI)为Pf(DS|Sa)与震害指数(damage index, DI)的乘积:

(12)

式中:DIj(j=1, 2, …, 5)为震害指数,根据文献[28],其与破坏状态的对应关系见表5。

表5 破坏状态及其对应的DITable 5 Damage states and corresponding DI

根据图6、式(12)和表5,得到结构的VI曲线如图7所示。

图7 模型Frame-C和Frame-UHPC易损性指数曲线Fig.7 Vulnerability index curves of Models Frame-C and Frame-UHPC

根据表1中的不同地震水准所对应的Sa及图7,得到模型Frame-C和模型Frame-UHPC所对应的VI如表6所示。可以看出,模型Frame-C在小震作用下的VI差异较明显,而中震和大震时2个模型的VI的差异逐渐减小。结合表1中不同地震水准所对应的Sa可以看出,相较于模型Frame-C,模型Frame-UHPC在小震作用下的VI减少了15.4%,中震时仅减少了2.4%,而大震时2个模型的VI基本相同。可知,在规范性态点下,模型Frame-C和Frame-C的易损性指数差异较小,UHPC结构不能充分发挥其高强、高韧的材料优势,因此有必要提高极限状态所对应的性态点。

表6 模型Frame-C和Frame-UHPC的易损性指数Table 6 Vulnerability indices of models Frame-C and Frame-UHPC

4 基于建议性态点的易损性分析

4.1 建议性态点的确定

为了更好地对UHPC结构进行地震风险预测和损伤评估,充分发挥UHPC的高强、高延性等材料优势。通过对文献[7, 9-10]中的26根配筋UHPC柱进行分析,得到其弹性层间位移角θe和弹塑性层间位移角θp的均值见表7。

表7 配筋UHPC柱的θe和θpTable 7 θe and θp of steel reinforced UHPC columns

表8 不同性态点下极限状态概率对比Table 8 Comparison of limit states probability under different performance points

通过数据分析,得到满足95%保证率的θe和θp分别为1/234和1/45。据此,定义配筋UHPC框架结构的LS1、LS2、LS3、LS4对应的层间位移角中位值分别为:1/250、1/120、1/50、1/25。

4.2 基于建议性态点的极限状态概率

根据式(9)和式(11)可知不同性态点划分下,模型Frame-UHPC的Pf(LS1|Sa)、Pf(LS2|Sa)不同,其对比如图8所示。可以看出,在建议性态点下,模型Frame-UHPC达到极限状态的概率明显更小。与规范性态点相比,使用建议性态点时Sa,FE、Sa,ME和Sa,MCE所对应的Pf(LS1|Sa)分别下降了46.2%、10.7%和2.67%,Pf(LS2|Sa)分别下降了35.0%、8.48%和7.8%。

4.3 基于建议性态点的破坏状态概率

规范性态点和建议性态点下,模型Frame-UHPC的Pf(DS1|Sa)、Pf(DS2|Sa)和Pf(DS3|Sa)对比见图9。可以看出,相较于规范性态点,使用建议性态点评价时模型Frame-UHPC处于DS1状态的概率明显较高,而处于DS2和DS3状态的概率则更低,且Pf(DS2|Sa)max和Pf(DS3|Sa)max所对应的Sa也有所提高。

图9 不同性态点下的破坏状态概率曲线Fig.9 Damage state probability curves under different performance points

4.4 基于建议性态点的结构损伤评估

规范性态点和建议性态点下,模型Frame-UHPC的VI如图10和表6所示。可以看出,由于提高性态点指标后结构达到破坏状态概率减小,使用建议性态点时模型Frame-UHPC的VI更小。相较于规范性态点,建议性态点下模型Frame-UHPC在Sa,FE、Sa,ME和Sa,MCE时所对应的VI分别减少了31.8%、17.5%和3.8%。

图10 不同性态点下模型Frame-UHPC的易损性指数曲线Fig.10 Vulnerability index curves of Model Frame-UHPC under different performance points

相较于规范性态点下的模型Frame-C,建议性态点下模型Frame-UHPC在Sa,FE、Sa,ME和Sa,MCE时所对应的VI分别减少了42.3%、19.5%和5.6%,更符合UHPC良好抗拉、抗压和裂后工作能力对结构抗震性能贡献的预期。

5 结论

1)规范性态点下,相较于模型Frame-C,模型Frame-UHPC达到最大中等破坏或严重破坏状态概率时对应的地震动强度更大,表明模型Frame-UHPC在强震作用下具有更好的抗震能力。

2)规范性态点下,模型Frame-C和模型Frame-UHPC的易损性指数相差在16%以内,不能充分体现UHPC结构的材料优势。

3)通过对文献中配筋UHPC柱试验结果的整理和分析,给出了适用于模型Frame-UHPC的建议性态点。与规范性态点相比,建议性态点下模型Frame-UHPC的达到极限状态的概率更低,小震和中震所对应的极限状态概率分别下降了46.2%和10.7%;易损性指数明显减小,小震和中震所应对的易损性指数分别减小了19.5%和42.3%。因此,建议性态点下模型Frame-UHPC可以更好地发挥其材料优势。