近断层地震下连续梁桥随机振动与易损性分析

周政, 唐光武, 高文军, 陈国海, 杨迪雄

(1.大连理工大学 工程力学系,工业装备结构分析优化与CAE软件全国重点实验室, 辽宁 大连 116024; 2.招商局重庆交通科研设计院有限公司, 重庆 400067)

混凝土连续梁桥结构作为交通运输网络中的关键节点,对于保障交通路网的安全运行与健康发展发挥着至关重要的作用。鉴于连续梁桥在桥梁工程领域的广泛代表性,开展量大面广的连续梁桥随机振动响应和地震易损性分析显得尤为必要,并以此来提升连续梁桥的抗震安全。诸多震后灾害调查表明,相较于普通的远场地震动,近断层地震动具有明显的长周期、大幅值速度脉冲,这会使桥梁产生较大的地震动力响应和结构破坏[1]。因此,开展关于近断层地震动作用下连续梁桥随机动力响应和地震易损性分析具有重要意义。

近年来,国内外一些学者对近断层地震动作用下桥梁结构地震动力响应进行了研究。Li等[2]采用非线性时程分析方法和反应谱分析方法,对近断层地震动作用下连续梁桥开展了全桥地震响应分析,发现近断层脉冲响应显著增强了其地震动力响应。Zhong等[3]同样利用非线性时程分析方法探究了近断层地震动的脉冲效应对简支梁桥的抗震安全性的影响。研究结果表明,近断层地震动的脉冲效应会加大简支梁桥受到的地震破坏,且距断层越近,简支梁桥破坏的风险越高。采用非线性时程分析方法,国巍等[4]考察了考虑桩土相互作用和活动支座摩擦力的高铁桥梁在竖向近断层地震动作用下的破坏特征。研究结果表明,高铁简支梁桥的破坏部位多集中于梁缝处和活动层等上部轨道结构,桥墩破坏并不严重。

因为地震动呈现较强的随机性,研究者开展了桥梁随机振动的研究。Lin等[5]针对大跨斜拉桥三维模型,采用虚拟激励法考察了地震动的空间相干性对随机振动响应的影响,发现地震动的行波效应对于大跨度桥梁的随机地震响应影响显著。然而,虚拟激励法仅适用于线性或弱非线性结构随机振动分析。基于概率密度演化方法,Yu等[6]考察了轨道随机不平顺下车桥耦合系统的随机振动响应,指出随着列车速度的增加,车桥耦合系统的随机振动响应的均值和标准差也随之增大。但概率密度演化方法需要求解广义概率密度积分方程,求解该方程的计算成本高。此外,Yu等[7]基于时域显式方法计算了轨道随机不平顺激励下车桥系统的非平稳随机振动响应。然而时域显式方法难以应用于桥梁非线性随机振动分析。近断层随机地震动作用下连续梁桥的随机振动分析。既有分析方法在处理该问题上存在着或多或少的缺点,限制了大型桥梁结构随机动力学分析效率。因此,构建高效的非线性随机振动分析的理论框架,探究桥梁结构中非线性与随机性耦合机理,仍是十分必要的。

地震易损性分析是基于性能地震工程研究的重要环节。地震易损性是指在某一个场地对于一定的地震动强度指标下结构达到或超过规定的功能水平的概率,其中规定的功能水平对应于结构的破坏状态。而地震易损性分析方法大体上可分为2类[8-13]:1)基于传统的概率地震需求模型,即假设结构地震响应与地震动强度指标之间满足对数正态分布假设,以此来建立易损性曲线。主要包括概率地震需求分析(probabilistic seismic demand analysis, PSDA)、增量动力分析方法、极大似然估计法等方法;2)利用可靠度理论方法来计算不同地震动强度下桥梁结构达到不同破坏状态的超越概率,从而绘制地震易损性曲线。尽管第1类简化的地震易损性分析方法目前在桥梁抗震安全领域应用较为广泛[9-11],但是这类方法忽视结构系统的物理过程和力学行为,基于人为的易损性函数满足累积对数正态分布的假设计算易损性曲线,计算误差大、适应性差。从定义可知,地震易损性分析本质上就是一个动力可靠度计算问题。因此,也有一些学者采用第2类地震易损性分析方法,即利用可靠度分析方法来计算结构的地震易损性。Tsompanakis等[12]利用蒙特卡模拟(Monte Carlo simulation, MCS)方法获得了路堤边坡的地震易损性曲线,并将计算结果同常见的满足对数正态经验分布的易损性模型进行了比较。Huang等[13]基于概率密度演化方法研究了挡土墙结构在随机地震作用下动力可靠度以及地震易损曲线。关于桥梁的地震易损性研究,吴子燕等[14]在考虑地震动以及结构本身的随机性下,采用MCS建立了一座四跨连续梁桥的地震易损性曲线。谢立夫[15]采用基于Kriging模型的响应面方法,计算了不同地震动强度下斜拉桥的可靠度,进而建立了典型斜拉桥模型的地震易损性曲线,提高了传统桥梁地震易损性分析的效率。但是,第2类地震易损性分析方法往往需要在不同地震动强度条件下进行大量的确定性振动分析,计算代价大。值得指出的是,对于桥梁结构的随机振动响应和地震易损性分析,过去通常是采用不同的方法求解的,缺少通用高效的计算方法。

为此,本文利用作者团队近期提出的统一准确的随机动力学分析框架:直接概率积分法(direct probability integral method, DPIM),将其同时应用于近断层随机地震动作用下非线性连续梁桥的随机振动响应与地震易损性分析中。其中针对近断层脉冲型和无脉冲随机地震动作用,利用DPIM准确求解非线性与随机性强相互耦合的连续梁桥非线性随机振动响应的概率密度函数(probability density function, PDF)。然后考虑不同峰值地面加速度(peak ground acceleration, PGA)和4种破坏状态,准确地分析连续梁桥的地震易损性,进而绘制易损性曲线,为桥梁抗震设计安全评价提供新途径。

1 基于DPIM的随机振动响应分析

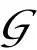
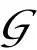
(1)

式(1)表征的映射关系本质上是系统的控制方程,它可以是显式也可以是隐式形式。而本文的控制方程是隐式的连续梁桥结构动力学平衡方程,可采用逐步积分法获得所关心的结构响应。

随机动力系统的随机事件所携带的概率在整个物理演化进程中始终保持不变,此即为概率守恒原理[16-18]。概率守恒原理与能量守恒定律和质量守恒定律一样,是物理系统遵循的基本原理。由此可知,随机输入事件与随机输出事件的概率相等,即:

(2)

式中:pY(y,t)、pΘ(θ)分别为输出随机向量Y和输入随机向量Θ的概率密度函数;ΩY和ΩΘ分别表示输入和输出随机向量所对应的样本空间。

根据概率守恒原理,结合随机输入响应Θ和随机输出向量Y之间的物理映射关系,可以推导出两者的PDF演化关系,即概率密度积分方程(probability density integral equation, PDIE)[17]为:

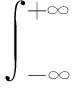
(3)

式(3)刻画了随机动力系统响应概率密度函数pY(y,t)的传播机制。它是一个含狄拉克不光滑函数的多维积分方程。由PDIE可知,一旦表征动力系统物理演化过程的映射关系确定,就可以计算得到不同时刻输出向量Y的概率密度函数,且对于任意时刻随机动力系统总是满足概率守恒原理的。

对于非线性连续梁桥系统而言,借助PDIE可以获知随机地震动激励与随机地震输出响应之间的概率密度函数对应关系。然而考虑了非线性性质的连续梁桥结构所确定的物理映射隐式关系复杂,且概率密度积分方程中包含了不光滑的Dirac函数,上述原因导致了概率密度积分方程解析求解困难。为此Chen等[17-18]提议了2个关键技术来解决上述问题:1)借助于基于广义F偏差选点方法[19]生成代表点,并利用沃罗诺伊剖分对输入概率空间进行剖分;2)利用高斯函数近似代替狄拉克函数,以获得较光滑的概率密度函数曲线,上述具体过程请参见文献[17-19] 。

因此,借助DPIM可以将表征随机性传播的概率演化过程与包含非线性特性的物理方程进行解耦,高效求得受随机近断层地震动激励下非线性连续梁桥系统随机振动响应的概率密度函数、均值、标准差等概率信息。

2 基于直接概率积分法的连续梁桥地震易损性分析

由前文可知,第2类地震易损性分析方法利用可靠度分析技术,以计算不同地震强度条件下达到或超过某种破坏状态的超越概率来建立地震易损性曲线。相关研究所采用的方法虽严格满足基于性能地震工程理论框架的定义,但应用过程中难免会出现计算时间长、计算成本高等问题[13]。为此,本文把DPIM推广用于计算不同地震动强度下结构的动力可靠度,鉴于可靠度数值与结构破坏状态超越概率之和为1,从而可以得到不同地震动强度条件下连续梁桥结构达到或超过不同破坏状态的超越概率(即失效概率),最终得到地震易损性曲线。

2.1 基于DPIM的地震易损性分析

对于受随机近断层地震动作用的非线性连续梁桥系统,基于DPIM进行动力可靠度分析中,需要明确动力可靠度分析的功能函数:

Z(t)=g(Θ,t)=Ythd-Y(Θ,t)

(4)

式中:Ythd为地震易损性分析时不同破坏状态对应的阈值;Y(Θ,t)为随机地震动样本激励作用下连续梁桥系统的非线性时程响应,可利用有限元方法计算获得。

在动力可靠度分析过程中,理论上需要考虑近断层地震动作用下每个时刻连续梁桥非线性随机振动响应值,这无疑会大大增加计算工作量。为此,本文基于首次超越破坏准则,采用等效极值映射的方法计算连续梁桥的动力可靠度,进而得到其地震易损性曲线。

依据DPIM,可构造出时间区间(0,t]内响应的等价极值映射[18]:

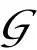
(5)

根据基于首次超越破坏准则[18]的动力可靠度方法,当结构的极值响应超过规定的阈值时,结构就会发生失效。因此连续梁桥结构的动力可靠度表示为:

R(t)=Pr{Yext(Θ,τ)∈Ωs,τ∈(0,t]}

(6)

式中:Yext为连续梁桥系统的极值响应;Ωs为连续梁桥系统的安全域。

同样根据等效极值原理,构造新的功能函数关系为:

Z(t)=g(Θ,t)=Ythd-Yext(Θ,t)

(7)

根据PDIE和式(7),连续梁桥的动力可靠度可以表示为:

(8)

鉴于狄拉克δ函数与海维赛德功能函数之间满足关系式:

δ(z)=dH(z)/dz

(9)

将式(9)代入到式(8)中,最终得到连续梁桥系统的动力可靠度计算公式为:

(10)

式中:θq和Pq分别为基于GF偏差选点方法[19]生成的代表点及其赋得概率。

因此,连续梁桥在不同地震动强度下的失效概率为:

(11)

基于DPIM可以获知在给定地震动强度条件下连续梁桥构件的动力可靠度数值以及失效概率,依据第2类地震易损性分析方法,即不断调整地震动强度参数(intensity measure, IM),获得对应地震动强度条件下达到或超过结构不同破坏状态的失效概率,最终得到非线性连续桥梁系统的地震易损性曲线。

为了利用动力可靠度分析的直接概率积分法进行连续梁桥地震易损性分析,本文采用Yang等[20]提出的包含最强速度脉冲方向的近断层地震动随机模型,基于该模型来生成随机近断层地震动激励。

2.2 连续梁桥地震易损性分析的损伤指标和破坏状态确定

地震易损性分析定义为在规定地震动强度条件下,结构地震需求超过规定破坏状态的概率。而IM的选择会直接影响评价连续梁桥结构抗震能力的准确性。常见的IM有峰值地面加速度、峰值地面速度、谱加速度Sa、谱速度Sv等,根据Padgett等[21]的研究,综合考虑了IM的效率、实用性和充分性等特点,选择PGA作为非线性连续梁桥地震易损性分析的IM参数。而我国需要进行桥梁抗震设计地区的地震烈度一般为6～8度,因此选择设计基本PGA的变化范围为0.1 g～0.6 g。

根据基于性能的抗震设计理论要求,结构在承受不同强度水平的地震时需要达到一组规定的预期性能目标。为区分连续梁桥结构在近断层地震动作用下进入不同的性能损伤状态,选择一个合适的损伤指标显得尤为重要。诸多桥梁地震响应的研究发现,桥梁支座剪切破坏和桥墩弯曲破坏是连续梁桥在地震作用中最容易出现的2种破坏类型,因此在应用DPIM进行连续梁桥的地震易损性分析中,选择支座剪切应变γ、桥墩墩顶的位移延性比μd以及桥墩墩底曲率延性比μφ作为损伤指标。

计算连续梁桥支座剪切应变γ、墩顶位移延性比μd以及墩底曲率延性比μφ的公式为:

γ=Δr/Δt

(12)

μd=Δd/Δcy1

(13)

(14)

在考虑支座的剪切应变γ、桥墩的位移延性比μd和曲率延性比μφ3种损伤指标的基础上,将连续梁桥地震破坏状态划分为:无损坏(LS0)、轻微破坏(LS1)、中等破坏(LS2)、严重破坏(LS3)和完全破坏(LS4)5个不同的等级,以满足区分不同性能破坏状态的要求。根据Alam等[22]的研究,这里给出了连续梁桥支座和桥墩的破坏状态划分的损伤指标数值,如表1所示。

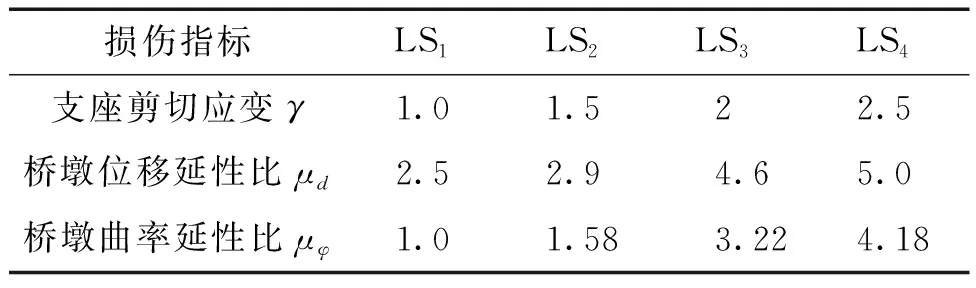
表1 连续梁桥地震破坏状态的量化描述Table 1 Quantitative description of seismic damage states of continuous girder bridge

3 连续梁桥非线性随机振动响应和地震易损性分析数值算例

本文建立了基于DPIM的连续梁桥非线性随机振动响应和地震易损性分析的新框架。本节采用一座典型的四跨非线性连续梁桥算例展示所提出框架的准确性。为了进一步说明近断层脉冲地震动对桥梁抗震性能的影响,还考察了近断层脉冲型和无脉冲地震动作用下连续梁桥的非线性随机振动响应以及地震易损性曲线。

3.1 桥梁结构有限元模型

桥梁算例的原型是一座单幅高速公路混凝土连续梁桥[23],跨径布置为4跨,每跨长30 m,桥宽19 m。算例中连续梁桥的上部结构主梁设置为预应力T梁结构,材料为C40混凝土;下部结构为排架墩结构,每个桥墩由3个直径为1.4 m的圆柱和长宽数据为2 m、1.6 m的矩形盖梁组成,材料均为C30混凝土,桥墩高均为10 m;桥台设置为由桩基支撑的座式桥台,桥台总高为9.7 m,背墙高度为2.2 m。连续梁桥模型立面图如图1所示。

图1 连续梁桥模型立面图Fig.1 Elevation of continuous girder bridge model

本文基于OpenSees有限元平台[24]建立了桥梁的三维非线性有限元模型,总自由度数为1 092,用以模拟算例桥梁模型在近断层地震动作用下的非线性地震响应。在我国抗震设计规范中,主梁和盖梁是基于能力保护构件的设计原则进行设计,为使主梁和盖梁在地震作用下保持弹性状态,因此OpenSees程序中,主梁和盖梁均采用弹性梁柱单元(elastic beam column element)来进行模拟,其弹性模量分别为3.25×104MPa与3×104MPa,泊松比均为0.2。考虑到桥墩的顶部和底部在地震动作用下会出现塑性铰,为此本文采用基于力的梁柱单元(force-based beam-column element)来进行模拟,其中桥墩的保护层混凝土和核心混凝土均是由Concrete04材料定义,表2整理了2种混凝土本构模型的具体参数,包括最大抗压强度fc、混凝土峰值强度下的应变ec、混凝土屈服强度下的应变ecu以及初始刚度Ec,桥墩的纵筋和箍筋均是由Steel02材料定义,其中钢筋的屈服强度和初始弹性模量分别为378 MPa和200 GPa。桥墩墩顶设置板式橡胶支座,桥台台顶设置铅芯橡胶支座,2种支座均采用弹性体支座单元(elastomeric bearing element)进行模拟,其中板式橡胶支座和铅芯橡胶支座的竖向承载刚度分别为2.67×106kN/m和1.69×106kN/m,等效水平刚度分别为2 965 kN/m和9 600 kN/m。本文采用撞击材料(impact material)来模拟地震作用时连续梁桥主梁与桥台之间的碰撞关系,其中碰撞刚度设置为1.94×106kN/m。在算例中由于没有考虑到地震作用中桩土效应的影响,因此桥墩和桥台底部均采用固结处理。

表2 连续梁桥混凝土本构模型材料参数Table 2 Material parameters of concrete constitutive model for continuous beam bridge

3.2 近断层地震动作用下连续梁桥非线性随机振动响应

采用DPIM和MCS方法计算了3种PGA下近断层脉冲型地震动对于连续梁桥主梁跨中节点位移极值响应的PDF。同时,考虑到现有地震易损性分析方法中常假设结构极值响应的PDF满足对数正态分布形式,因此本文还建立了主梁跨中节点极值位移响应满足对数正态分布(lognorm)形式的PDF,并用极大似然估计方法确定了PDF的具体参数。最终得到主梁跨中节点位移极值响应的PDF曲线,结果如图2所示。为进一步量化PDF曲线之间的差异,将MCS方法得到的位移极值响应的PDF曲线设置为基准。采用比较观察频数的卡方检验方法(chi-squared test)对DPIM计算得到的PDF及满足对数正态分布假设的PDF曲线进行检验,其中卡方值(Chi)衡量了计算得到的PDF曲线同基准PDF曲线之间的偏离程度,若卡方值越大则表明两者间的偏离程度越大。相应的计算结果如表3所示。

图2 连续梁桥主梁跨中节点位移极值响应Fig.2 Extreme-value displacement response of mid-span joint of continuous girder bridge

表3 连续梁桥主梁跨中节点极值位移响应PDF曲线的卡方检验统计Table 3 Chi-square test statistics of extreme-value displacement response of mid-span joint of girder bridge

从图2(a)、(b)和(c)可见,无论近断层脉冲型地震动的PGA如何变化,DPIM和MCS方法计算得到的主梁跨中节点位移极值响应的PDF始终吻合较好,这表明DPIM可以准确得到桥梁结构的随机振动响应。而从表3可见,在不同PGA近断层脉冲型地震动作用下,对DPIM进行拟合优度评价的卡方值要明显小于极值响应PDF满足对数正态分布形式的卡方值,这表明基于DPIM计算得到的桥梁极值响应PDF曲线在整体上误差更小,进一步证明了基于DPIM方法解决桥梁随机振动的精确性。

同时注意到,当近断层脉冲型地震动的PGA较小时,满足对数正态分布形式的桥梁位移极值响应PDF曲线同样与MCS结果吻合较好,但随着PGA的不断增加,两者出现了显著的差异。这表明在地震动强度较低的水平下,常用地震易损性分析方法(如PSDA、增量动力分析等)预先设定的假设具有一定的合理性,但随着地震动强度增大,传统地震易损性分析方法所作假设并不能准确预测桥梁极值响应实际真实的PDF,这也会进一步影响基于传统地震易损性分析方法绘制地震易损性曲线的精度。

值得指出的是,在给定近断层脉冲型地震动PGA条件下,采用DPIM方法进行随机振动分析仅用时266 min,而相同条件下采用MCS方法的计算耗时约为DPIM的10倍,这也反映出DPIM在进行桥梁非线性随机振动分析的计算高效的优势。

3.3 近断层地震动作用下连续梁桥地震易损性分析

对连续梁桥模型施加不同PGA大小的近断层脉冲型地震动,其中PGA的变化范围为0.1～0.6g,并在此基础上分别采用DPIM、MCS和PSDA方法建立了4种破坏状态下桥梁中间支座剪切应变的地震易损性曲线,结果如图3所示。同时本文采用便于计算的K-L散度来描述DPIM和PSDA方法建立的地震易损性曲线与MCS得到的地震易损性曲线之间的差异程度,其中较小的K-L散度数值表明2种地震易损性曲线之间的差异性较小,反之亦然,最终将计算结果列于表4。

图3 连续梁桥中间支座剪切应变γ的地震易损性曲线Fig.3 Seismic fragility curves of shear strain γ of middle support of continuous girder bridge

表4 连续梁桥中间支座剪切应变地震易损性曲线的K-L散度检验统计Table 4 K-L divergence test statistics for seismic fragility curves of shear strain of middle support of girder bridge

观察图3可以发现,相比于PSDA方法,DPIM在4种破坏状态下建立的地震易损性曲线与MCS结果吻合更好。从表4中可以发现,4种破坏状态下DPIM计算得到的K-L散度数值均小于PSDA,这说明DPIM建立的地震易损性曲线结果更贴合MCS计算结果。以上结果表明,基于DPIM方法可以获得更加精确的地震易损性曲线。

此外,为探究含速度脉冲的近断层地震动对于桥梁地震易损性曲线的影响。本文基于3.1节中提到的近断层地震动随机模型[20],生成具有不同PGA大小的2种近断层地震动激励。采用DPIM分别计算了近断层脉冲型与无脉冲型地震动对于连续梁桥桥墩构件的地震易损性曲线,结果如图4所示。

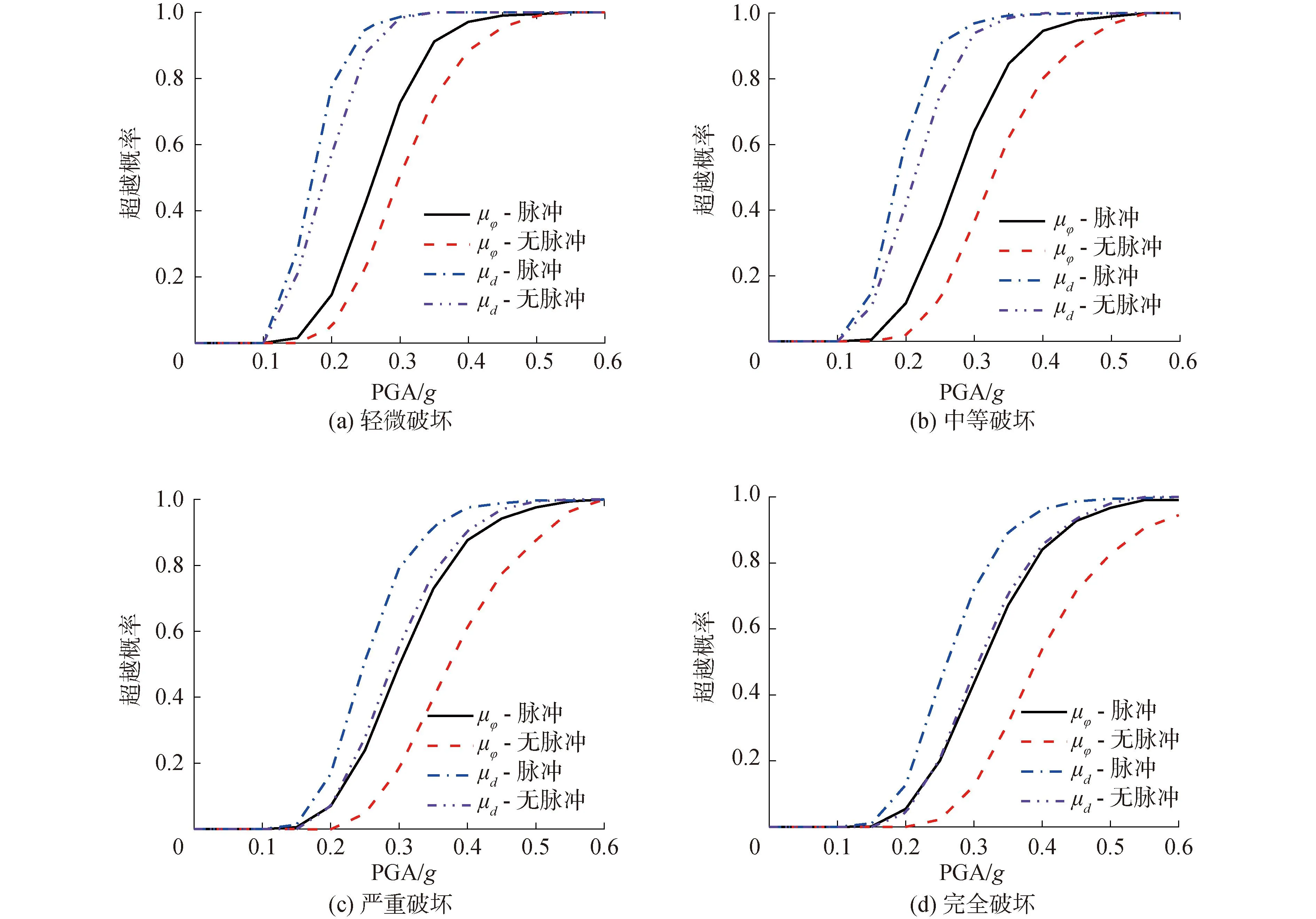
图4 近断层有/无脉冲地震动作用下中间桥墩墩顶位移延性比μd和墩底曲率延性比μφ的地震易损性曲线Fig.4 Seismic fragility curves of pier top displacement ductility ratio μd and pier bottom curvature ductility ratio μφ under near-fault ground motions with and without pulses

观察图4可以清楚发现,近断层脉冲型地震动作用下的桥墩构件地震易损性曲线始终出现在无脉冲型地震动作用下地震易损性曲线的上侧,这表明近断层地震动的速度脉冲会显著增加桥梁结构进入不同破坏状态的超越概率,进一步放大桥梁所受到的地震破坏。同时还发现,当考虑桥梁构件不同损伤指标时,所建立的地震易损性曲线出现了明显差异,其中考虑桥墩墩顶位移延性比损伤指标的超越概率在4种破坏状态下均大于考虑墩底曲率延性比指标的超越概率。因此,在进行桥梁抗震安全分析时,应尽可能多地考虑不同的损伤指标或从桥梁系统的角度上进行地震易损性分析,以达到充分评价桥梁抗震能力和地震安全性的目的。

为进一步量化近断层地震动的速度脉冲对于桥梁结构所受地震破坏的影响,本节筛选了图4所示的严重破坏以及完全破坏状态下桥墩构件损伤超越概率进行了比较分析,结果列于表5、6中。而由表5、6可知,近断层地震动的速度脉冲在不同地震动强度条件下对桥梁破坏超越概率产生不同的影响,其中在地震动强度较弱时会显著放大桥梁的破坏超越概率,但随着地震动强度增加,这种放大现象也逐渐减弱。因此在进行桥梁地震易损性分析中还应考虑不同近断层脉冲型地震动强度的影响,以提高桥梁结构的抗震性能和安全水平。

表5 近断层有/无脉冲地震动作用下中间桥墩严重破坏状态超越概率的比较Table 5 Comparison of exceedance probabilities for severe damage state of middle pier under near-fault ground motions with and without pulses

表6 近断层有/无脉冲地震动作用下中间桥墩完全破坏状态超越概率的比较Table 6 Comparison of exceedance probabilities for complete damage state of middle pier under near-fault ground motions with and without pulses

4 结论

1) 基于DPIM方法可以准确高效地计算出不同地震动强度下连续梁桥结构的随机振动响应,并在此基础上建立了刻画连续梁桥结构进入不同破坏状态的地震易损性曲线,这为桥梁抗震性能安全评价提供一条新的途径。

2) 包含大幅值、长周期速度脉冲的近断层地震动会加剧连续梁桥结构受到的地震破坏,使得连续梁桥构件进入不同破坏状态的超越概率出现明显的增加,并且这种增加幅度受到地震动强度的影响,同时考虑桥梁不同损伤指标所建立的结构地震易损性曲线也有所不同。因此在进行桥梁地震安全分析时,需要格外注意不同强度大小的近断层脉冲型地震动以及相关桥梁损伤指标划定的影响。

3) 参数化地震易损性分析PSDA方法常假设结构的极值响应PDF满足对数正态分布形式,经过验证,这种假设在地震动强度较小的条件下与结构极值响应的真实PDF曲线吻合较好,但随着地震动强度增加,两者出现明显偏差。而在此基础上,参数化地震易损性分析方法建立的易损性曲线并不能充分反映桥梁结构的抗震性能,这也体现了基于DPIM建立桥梁结构地震易损性曲线的优越性。

本文所提出的新框架可高效地获得连续梁桥等大型非线性结构的随机动力响应,并且准确得到其地震易损性曲线。在未来的研究中,可将此框架拓展应用于斜拉桥、悬索桥、拱桥等抗震性能安全评定,为大型基础设施系统地震风险管理与控制提供通用、高效的新方法。