基于ISM法的中英初中数学教材比较研究

吴佳敏　林子植

摘      要 ISM法（解释结构模型）經过修正和实践已经是一种比较成熟的分析教材结构的科学方法。运用ISM法对中国沪教版和英国CCM版初中数学教材中“概率”内容的知识结构进行分析，通过抽取知识要素、确定要素间关系和邻接矩阵、绘制要素层级分布图，对教材的逻辑顺序从起始要素安排、知识要素选取、各要素间关系和最高要素安排四个方面的异同点进行梳理和对比。基于研究结果对教材编写提出知识要素的选取注重知识的深度和联系性；知识结构的编排重视内在逻辑紧密和整体化；知识要素的价值取向加强与跨学科内容融合的建议。对教师教学提出基于知识要素的呈现特点把握教学重难点；基于知识结构的编排优化大单元教学设计；基于知识编排的顺序统筹规划教学序列的建议。

关 键 词 解释结构模型法（ISM法）；初中数学教材；概率；知识要素层级；中英教材比较

引用格式 吴佳敏，林子植.基于ISM法的中英初中数学教材比较研究[J].教学与管理，2024（12）：73-77.

2022年教育部颁布《义务教育数学课程标准（2022年版）》（以下简称《标准（2022版）》），为全面落实立德树人的根本任务和进一步深化课程改革提供了纲领性文件[1]。教材作为课程标准的重要载体，是课程标准的具体化，在基础教育改革中处于基础性、战略性的地位。随着基础教育课程改革的不断推进，中小学教材的研究逐渐成为数学教育研究的热点[2]。教材知识内容的编写质量和顺序结构对课程改革的成败起着举足轻重的作用[3]。国内外教材的对比研究是编写和完善教材的重要途径之一，通过对比我国与不同国家的教材，借鉴他国教材中的长处，从而完善我国教材。

ISM（Interpretive Structural Modeling Method）法，即解释结构模型法，是一种运用于解决较为复杂的社会经济系统问题的理论方法。在当前的教学理念中，ISM法可以将教材内部知识要素凌乱错落的关系，结合自身主观认识和经验整理成客观清晰的结构模型[4]，对教材的结构进行量化分析最终以可视化的方式呈现，构建教材的知识结构模型，促进教师和学生对教材的理解。随着对ISM法研究的不断深入，发现有不少学者将ISM法运用于地理、物理、化学和数学等多个学科领域的教材分析中。原玉娟和徐章韬用ISM法分析人教A版高中数学必修系列5册教科书，指出教科书的教学序列安排[5]；吕超等人结合《抛物线》实例展示将ISM法应用于教材分析的意义[6]；曹月使用ISM法分析人教A版和北师大版指数函数和对数函数，得到两个版本教材关于指对函数的编写特点[7]；杨莉运用ISM法对人教版、英国CIE版以及澳大利亚IB版关于高中数学教材的“复数”内容实际编排顺序进行比较分析，得到各个版本的要素之间的关系[8]；郑金借助修正后的ISM法对人教A版和苏教版数学必修4的各章知识内容进行梳理，得出不同编排顺序的优劣势[9]。

ISM法经过修正和实践已经是一种比较成熟的分析教材结构的科学方法，但从已有的研究中发现涉及数学学科领域的教材分析较少，主要集中在高中数学教材分析，且以国内的各个版本的比较为主。在大数据时代，概率素养是当今公民需要具备的一项不可或缺的数学素养[10]。因此，本文以“概率”内容为例，通过借助ISM法对上海教育出版社出版的初中数学教材和英国剑桥大学出版社出版的《Cambridge Checkpoint Mathematics》（以下简称“沪教版”和“CCM版”）进行比较，以期为新教材编写工作提供理论依据，为教师教学提供一定参考。

一、研究设计

1.研究对象

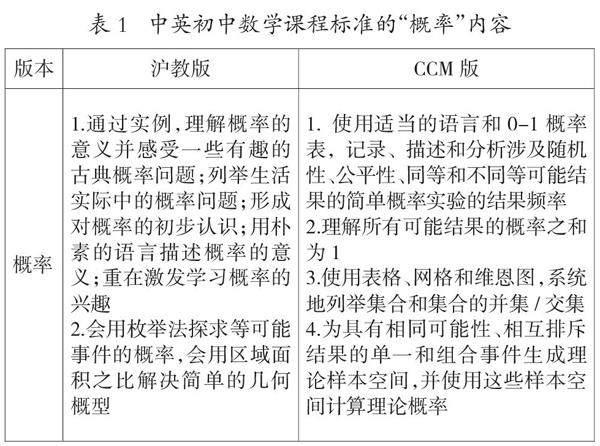
课程标准在各个国家的教育改革中起着纲领性的作用，是教材编写的主要依据。本文选取了2019年出版的中国沪教版初中数学教材和2013年出版的英国CCM版初中数学教材作为研究对象。两个版本的教材是根据各自国家的课程标准编写，中国沪教版依照2004年《上海市中小学数学课程标准（试行稿）》[11]，英国CCM版依照2007年《国家数学课程》进行编写[12]。根据两个版本教材中关于“概率”的内容要求，选取两个版本教材关于“概率”的具体章节内容（见表1），其中沪教版涉及“概率”的章节分布在八年级下册第二十三章“概率初步”，CCM版涉及概率的章节分别分布在七年级Unit16 Probability、八年级Unit15 Probability和九年级Unit16 Probability。

2.研究方法

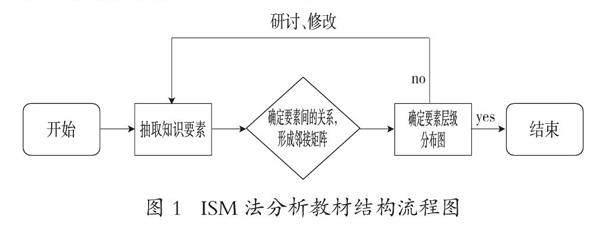
运用ISM法可以将教材内部知识要素间杂乱无章的关系整理成清晰明确的递阶结构模型，对教材进行量化研究形成相应的知识结构图，以此实现教材分析的科学性、严谨性和直观性。ISM法分析教材的具体操作步骤如图1所示。

3.研究过程

（1）抽取知识要素

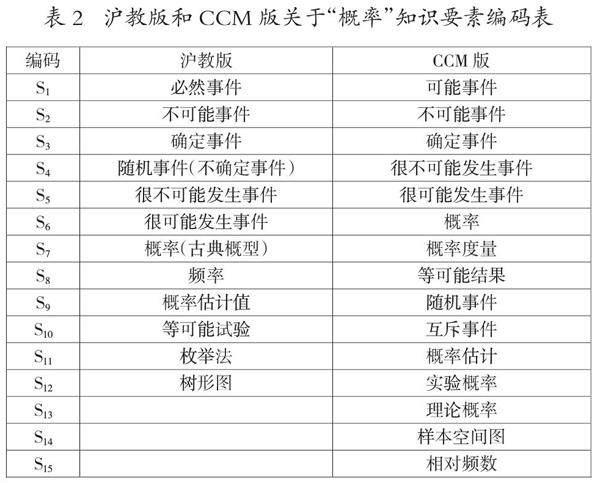
按照研究方法对知识要素进行抽取，结合两国课标中关于“概率”的内容标准整理知识要素，为了保证教材研究的科学性和客观性，知识要素的抽取要满足以下三个条件：①教材明确提出且字体加粗的概念；②教材主要的知识点；③在教材中处于承上启下的地位。结合这三个条件，对沪教版和CCM版“概率”内容主题抽取知识要素，并对其进行编码（见表2）。

（2）确定要素间关系，形成邻接矩阵

根据ISM法的规定，为了最大程度减少确定要素间形成关系的主观判断，明确要素间的关系，需准确把握教材的知识结构，按照教材的实际编排顺序。若学习者想掌握要素S2，则先要学会和掌握要素S1，则称要素S1和S2之间存在“直接关系”，称S1为先行要素，S2为可达要素。根据表2抽取的知识要素和上述定义，对沪教版和CCM版的“概率”知识要素进行“直接关系”分析（见表3）。

根据沪教版和CCM版教材关于“概率”知识要素直接关系表，形成邻接矩阵。对表3进行分析形成双向形成表格，其中纵轴表示“先行要素”，横轴表示“可达要素”，两者若有直接关系，则用“1”标记，若两者不存在关系则用空格表示，其次将沪教版和CCM版的双向形成表格用邻接矩阵表示，根据可达要素的个数（M），绘制一个M*M的矩阵，在矩阵中将双向形成表格中的空格用“0”来表示，表格中“1”不变，将邻接矩阵定义为A，得到邻接矩阵后利用Matlab软件进行编程求出可达矩阵P，其中表示可达要素到要素之间存在直接或间接的关系，0表示可达要素到要素之间不存在直接或间接的形成关系（不考虑两个要素之间链接路径的长度）。

（3）形成要素层级分布图

根据可达矩阵运算要素层级分布并绘制要素层级分布图。首先明确可达和先行集合的概念定义：可达集合P（si）是从要素si出发能到达的全部知识要素的集合；先行集合A（si）是所有能达到的知识要素si的集合。若满足P（si）∩A（si）=P（si），则称要素si为该层级的最高层级。通过以上步骤，对沪教版和CCM版的“概率”知识要素进行处理，得到两个版本知识要素层级分布表（见表4）。

根据表4的两个版本“概率”知识要素层级分布表可以发现，沪教版有10层目标，CCM版有9层目标，从低层到高层绘制要素层级有向图（如图2）。

二、研究结果与讨论

通过上述步骤得到沪教版和CCM版关于“概率”知识要素层级有向图，可以发现沪教版一共涉及10个层级，CCM版涉及9个层级，根据两个版本的层级有向图从起始要素安排、知识要素选取、各要素间关系和最高要素安排四个方面进一步比较。

1.起始要素安排的异同

要素层级有向图中最低层级的要素，只有指出箭头，没有指入箭头。沪教版和CCM版的起始要素略有不同，但均是让学生明确事件发生的可能性。沪教版选取“必然事件”作为起始要素，描述在一定条件下必定会出现的现象。采用4个日常生活例子引出关于不同事件的概念，引导学生从现实生活情境中初步理解概率知识。CCM版以“可能事件”作为起始要素，描述某一事件发生的可能性，直接通过给出事件发生可能性大小的程度副词的相关定义，帮助学生理解在特定条件下某一现象发生的概率大小。可以看出，两个版本教材均在起始要素中渗透事件发生的可能性大小，感悟数据的随机性，初步形成数据意识。

2.知识要素选取的异同

通过对两个版本“概率”知识要素进行比较，发现中英教材对知识要素的选取存在共性与差异。首先从数量上，沪教版一共有12个知识要素，CCM版有15个知识要素，相差不大。其次从具体要素的选择上，两个版本教材关于“事件及其发生的可能性”上涉及知识要素的分类大体一致，其中沪教版的“枚举法”和“树形图”对应CCM版的“样本空间图”，CCM版囊括沪教版其他知识要素，虽命名稍有差异，但所指知识点内容是一致的。然而，CCM版比沪教版多“概率度量”“相对频数”和“互斥事件”等知识要素。“概率度量”用某事件发生的概率作为度量标准，是一个[0，1]之间的实数，等价于沪教版中的“古典概型”，但沪教版未将其进行细分。“相对频数”指相对于总数出现的次数，沪教版将其体现在频率中，未将其单独列出。“互斥事件”是沪教版未涉及的知识要素，是两个版本关于知识要素的主要不同点，国内关于“互斥事件”的知识要素在高中学段才出现明确定义，而CCM版在初中阶段出现。

3.各要素间关系的异同

通过比较两个版本知识要素层级有向图发现，两个版本在层级的分布编排上大体按照“事件及其发生的可能性大小—事件的概率—概率的计算”这一逻辑顺序循序渐进地呈现知识点内容。这种教材的编排方式符合学生认知发展规律，有利于学生由简单到复杂、由具体到抽象，循次而进地加深对于“概率”知识的理解。在具体知识的逻辑编排上，两个版本具有一定区别。沪教版和CCM版对于“事件及其发生的可能性大小”的相关概念采取不同的处理方式，沪教版按照必然事件、不可能事件到确定事件，从随机事件到很可能发生事件再到很不可能发生事件的次序依次展开，既包括归纳顺序也有演绎的逻辑顺序，CCM版主要以归纳的逻辑顺序进行编排知识点内容，从可能事件到不可能事件再到确定事件，让学生明晰事件发生可能性大小的相关概念。

4.最高要素安排的异同

要素层级有向图中最高层级的要素，只有指入箭头，没有指出箭头。沪教版牵涉的两个最高要素分别为“概率估计值”和“树形图”，通过画树状图的方法求出简单随机事件的所有可能结果，借助树状结构的分层特征，对某一事件发生的可能情况进行逐一枚举，从而直观求解，能够领悟在大量重复试验下，随机事件发生的频率具有穩定性，通过频率估计概率，初步构建学习概率内容所需的知识和方法。CCM版涉及四个最高要素分别为“随机事件” “互斥事件”“样本空间图”和“相对频数”，均是学习概率内容的最高要素，明晰“随机事件”和“互斥事件”的概念对计算和理解概率具有重要作用，“样本空间图”让学生学会列举所有可能发生情况，“相对频数”是学生通过列举之后进行统计所有可能发生的数量，巩固先前所学事件发生的可能性大小及概率求解的知识点内容。两个版本均将枚举法作为最高层级的知识要素，说明该知识要素是初中阶段学习概率内容的基本技能。

三、思考与建议

通过ISM法对中英两个版本初中数学教材“概率”内容的知识结构进行比较分析，试图把教材中关于概率内容的知识要素间的实质联系以层级有向图进行直观地展示，有助于研究者和教师更好地把握教材知识结构，为教材的编写和修订，教师的教学提供一定的参考。

1.关于教材编写的建议

（1）知识要素的选取注重知识的深度和联系性

在选取知识要素时，CCM版教材注重初高中内容的衔接，因此需要考虑知识的纵向和横向联系，利用知识间的联系和恰当的数学方法来促进深度学习，有利于学生高阶思维的发展[13]。高中知识的抽象概括性和初中知识具有一定跨度，这需要在初中阶段适当增加某些内容领域的基础知识要素，为之后学习打下基础。概率和统计相辅相成，需以联系的眼光看待。概率是推断统计的理论基础，概率是在特定条件下可收集到的研究数据，而推断统计是根据已有数据进行推测[14]。因此，教材对于概率知识要素的选取要为后阶段学习打下基础，同时注重与统计内容的联系。

（2）知识结构的编排重视内在逻辑紧密和整体化

CCM版在知识要素的逻辑编排上非常紧密，考虑学生现有的认知结构，并妥善地编排了各个知识要素。在充分理解课程标准和学生原有认知结构的基础上，教材的编排应注重知识之间的内在联系，并实现知识之间的相互转化，这有助于提高学生的思维品质，并促进学生构建完整的知识体系[15]。最新研究指出，学生需要先理解样本空间，即通过枚举法列举出试验的所有可能结果，才能量化某个事件发生的概率。因此，教材在概率内容的编排上应基于学生的认知水平，逐步过渡从定性认识到定量认识，从感知随机性到了解简单随机事件中所有可能发生的结果，并逐步感知和描述可能性的大小——事件概率[16]。

（3）知识要素的价值取向加强学科内容融合

两个版本在“概率”内容知识要素的选取上涉及该内容领域的核心概念，而数学具有方法的普适性、应用的广泛性和理性思维的独特性等特点，因此数学与其他学科融合有利于培养学生的数学核心素养[17]，以跨学科思维确定知识要素的价值取向，有助于学生系统地建构知识网络。选择学生熟悉的跨学科知识要素素材，以合适的问题情境创设，不仅能引导学生进行数学地分析、思考和反思，还可以激发学生的创新意识[18]，例如将航空航天、农业、医学、艺术、科学、工程、信息等对国家发展重要的知识素材融入到概率内容中，学生可以积累在未来从事的工作中通过概率知识来解决问题的经验。

2.关于教师教学的建议

（1）基于知识要素的呈现特点把握教学重难点

概率统计的目的是为了解决问题，而概率背后的基本知识要素是教学重难点[19]，对于数据、期望、分布、样本和抽样等思想都应该囊括其中。ISM法呈现知识要素的联系和层级结构有向图，将“概率”内容的知识要点呈层级性排列，教师通过知识要素的结构有向图把握基础要素和要素间的联系以及最高层级的要素，准确把握知识的重难点[20]，通过呈现沪教版和CCM版的层级结构有向图，教师以各要素间的衔接为依据，对教材的层次和脉络整体把握，对知识要素分类和分析，系统地组织教学内容，促进学生概率素养的形成和发展。

（2）基于知识结构的编排优化大单元教学设计

《标准（2022版）》重视数学学科知识的体系化，需要教师结合课标回归教材，关注概率内容的整体性。基于ISM法输出的知识要素层级图帮助教师把握和明晰概率知识的层次和整体结构。随机事件到古典概型再到概率估计值，体现知识生成性和层次性[21]。以ISM法对“概率”内容绘制整个内容领域的结构图，有助于教师对概率有系统和完整的把握，将零散繁杂但又紧密联系的知识要素形成有机整体，而大单元教学同样强调单元知识结构体系的构建，引领前后知识的联系。因此教师可以基于知识层级结构图进行大单元教学设计。

（3）基于知识编排的顺序统筹规划教学序列

利用ISM法对知识要素进行编排，为教师融合不同章节或单元的内容提供参考依据，调整教学序列，提高教学效率，帮助学生系统地把握整个知识内容框架，理清知识要素之间的关系，学生也可以将课堂中所学知识应用于解决现实生活中的问题，实现知行统一[22]。在日常教学中，教师应以ISM法对知识要素的梳理为基础，根据概率与实践的紧密联系，优化教学过程，提升课外实践水平，丰富学生的业余生活。同时，教师还应根据学生的认知规律，统筹规划整个概率内容的教学顺序，选取符合学生实际生活的问题进行教学[23]。

参考文献

[1] 中华人民共和国教育部.教育部印发《义务教育课程方案和课程标准（2022年版）》[EB/OL].（2022-04-08）[2023-02-27].http：//www.moe.gov.cn/srcsite/A26/s8001/202204/t20220420_619921.html.

[2] 邓翰香，吴立宝，曹一鸣.新世纪以来我国中小学数学教材研究热点、演进与展望——基于科学知识图谱的实证分析[J].教育理论与实践，2021，41（08）：38-43.

[3] 李玉琴.基于ISM法的高中数学新旧教材比较研究[D].大理：大理大学，2020.

[4]谭熙.基于ISM分析法的人教版新旧地理教材比较分析——以“地球上的水”为例[J].地理教学，2020（03）：42-45.

[5] 原玉娟，徐章韬.用ISM法确定系列教科书的教学序列——以人教A版高中数学必修系列教科书为例[J].数学教育学报，2017，26（02）：55-59.

[6]吕超，张巨俭.应用ISM法进行数学教材分析[C]//Information En-

gineering Research Institute，USA.Proceedings of 2012 International Conference on Education Reform and Management Innovation（E-

RMI 2012）Volume 5，2012：130-134.

[7] 曹月.基于ISM法的两个版本的数学教材比较——以指数和对数函数为例[J].高中数学教与学，2017（23）：1-4.

[8] 杨莉.基于ISM法的中英澳高中复数比较研究[D].厦门：集美大学，2020.

[9] 郑金.基于ISM法的数学教材比较研究实用性探讨[D].武汉：华中师范大学，2014.

[10][16] 何声清.“等可能性偏见”对初中生古典概率内容学习进阶的影响[J].数学教育学报，2022，31（06）：52-59.

[11] 上海市中小学（幼儿园）课程改革委员会.上海市中小学数学课程标准（2004年版）[S].上海：上海教育出版社，2004：70.

[12] GOV.UK.National curriculum in England：mathematics programmes of study[EB/OL].（2021-09-28）[2023-02-27].https：//www.gov.uk/government/publications/national curriculum in england mathe-

matics programmes of study.

[13]赵世恩，刘子钰.“问题导向”下促进深度学习的教学实践研究——以小学数学为例[J].课程·教材·教法，2023，43（01）：131-

137.

[14] 唐佳丽，李勇.“统计与概率”在小学数学教材中的编排分析[J].数学教育学报，2022，31（01）：59-63.

[15] 姜雨婧，刘小贤.基于ISM法对中美两版物理教材“电路”部分的结构分析[J].物理教师，2022，43（12）：68-71.

[17] 丁益民.用教材教：跨学科融合的数学教学[J].中学数学杂志，2022（11）：16-19.

[18] 孙虎，刘祖希.数学跨学科实践活动：“内涵”“价值”与“实施路径”[J].数学教育学报，2023，32（01）：19-24.

[19] 李亚琼，潘禹辰，徐文彬，等.高考概率与统计试题的统计与分析——以2021年全国课标卷为例[J].数学教育学报，2022，31（03）：20-25.

[20] 黄子珊，邱世藩.ISM法在高中地理大单元教学设计中的应用研究[J].中学地理教学参考，2022（08）：21-24+72.

[21] 李亚琼，徐文彬.高考课标卷概率統计试题的特点及其教学启示——基于2011—2020年全国课标卷的分析[J].数学教育学报，2021，30（06）：13-19.

[22] 谭远泊，黄翔.大单元教学视域下中学数学复习课教学研究[J].教学与管理，2023（06）：87-90

[23] 何勇刚，张立昌.基于结构方程模型的学习策略影响因素探究——以初中生学习“统计与概率”为例[J].数学教育学报，2020，29（01）：40-47.

[作者：吴佳敏（1998-），女，上海人，中南民族大学中华民族共同体研究院，博士生；林子植（1983-），男，江西九江人，江西科技师范大学大数据科学学院， 副教授，硕士生导师，博士。]

【责任编辑   王泽华】

*该文为2022年全国教育科学“十四五”规划教育部重点课题“学业成就测试中的表现标准建构方法研究”（DHA220399）的研究成果