沉井侧摩阻力监测装置设计及应用研究

肖 靖, 曾旭涛, 李嘉成, 陈培帅, 李德杰, 3

(1. 中交第二航务工程局有限公司, 湖北 武汉 430040; 2. 长大桥梁建设施工技术交通行业重点实验室, 湖北 武汉 430040; 3. 河海大学岩土工程科学研究所, 江苏 南京 210098)

0 引言

沉井作为基础形式,具有强度高、稳定性好、承载力高等优点,被广泛应用于桥梁、港口、地铁等工程建设中。沉井下沉过程中侧摩阻力的大小和分布规律是下沉阻力研究中的主要内容之一,同时能够明确侧摩阻力以及端阻力的占比,为沉井结构设计、下沉过程中助沉措施的制定、突沉和翻砂等预警提供可靠依据[1-2]。

目前,沉井侧摩阻力一般参考地质勘查给出的侧摩阻力标准值,或通过获取侧壁土压力,然后由侧壁土压力乘以摩擦因数得到侧摩阻力[3-5]。朱劲松等[6]通过现场监测沉井侧壁土压力求得侧摩阻力,并得出随着入土深度的增加,侧摩阻力与入土深度的关系曲线逐渐由线性变为二次抛物线形式。施洲等[7]开展了沉井侧摩阻力现场试验,发现当入土深度较大时,实测侧摩阻力值大于理论计算值。穆保岗等[8]、朱建民等[9]依托南京长江四桥北锚沉井,通过监测沉井下沉时侧壁土压力、井壁与土层的摩擦因数,得到了沉井侧摩阻力分布规律。在土与混凝土界面摩擦特性方面,Tehrani等[10]通过室内模型试验,得到混凝土表面粗糙度和土体的密实度制约着侧摩阻力的发挥; Llori等[11]研究发现,对于土-混凝土界面,法向压力影响着界面摩擦因数的取值,结构表面形态是影响土-结构界面摩擦因数的重要因素; 李梦瑶等[12]研究了不同含水率条件下粉土与混凝土界面的剪切力学特性,得到其界面剪切强度随着含水率的增大而逐渐减小,随着法向应力的增大呈线性增大的规律。目前关于沉井下沉时侧摩阻力的研究已取得显著成果,然而,地质勘查给出的侧摩阻力标准值是针对某一类土层的,实际工程地质条件复杂,采用此方法无法真实获取沉井下沉侧摩阻力; 另外,由于岩土特性及结构的复杂性,侧摩阻力发挥机制复杂,界面摩擦因数实测难度大[13],导致通过侧壁土压力和摩擦因数获得的侧摩阻力与实际存在一定差异[14-15]。

为此,针对沉井侧摩阻力无法直接获取的问题,本文设计一套新型的侧摩阻力直接监测装置,并在哈尔滨某沉井工程中进行应用,以验证装置的可靠性。

1 侧摩阻力监测装置构造及测试原理

1.1 侧摩阻力监测装置基本构造

在岩土工程试验中,三轴试验、环剪试验及直剪试验等均以特征剪切面的平均剪应力值代表某一点的剪应力。本文基于这个思路研制了侧摩阻力监测装置,其由箱体、基座、传力体、反力柱、拉压传感器、密封体等部分组成,如图1所示。该装置外轮廓尺寸为10 cm(长)×10 cm(宽)×8 cm(高)。箱体、基座、传力体均为硬质金属材料,密封体采用柔性防水密封材料; 传力体与箱体顶部预留一定间隙,防止剪切力作用时传力体与箱体发生接触,对应力值测定产生影响。

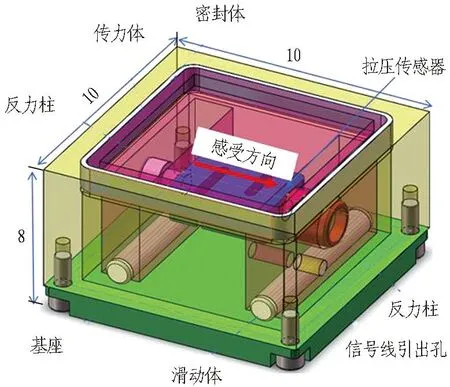
(a) 三维结构示意图(单位: cm)

1.2 拉压传感器工作原理及尺寸选择

1.2.1 拉压传感器工作原理

侧摩阻力装置中的拉压传感器为S形测力单元,应变片的贴片位置与悬臂梁结构相同。为了监测S形测力单元受力后产生的应变,将弹性元件的应变转换为电阻的变化。同时,为了提升传感器的灵敏度,剔除温度影响,粘贴4个应变片构成电阻应变全桥。拉压传感器示意如图2所示。

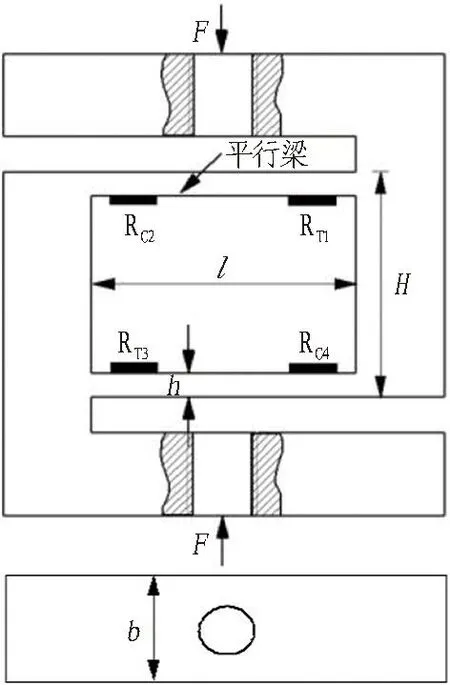
(a) S形测力单元

将S形测力单元等效为一端固定、一端悬臂的闭合框架结构进行受力分析,即在平行梁端部作用1个集中力F和1个逆时针的弯矩1/2Fl。其结构力学模型可简化为单跨超静定刚架,将刚架沿水平方向对称切开,有3对多余未知力,1对剪力X1,1对轴力X2,1对弯矩X3,该超静定结构基本受力体系如图3所示。

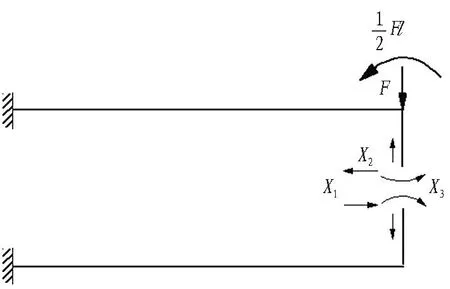
图3 超静定结构基本受力体系

为求解3个未知力,建立方程如式(1)所示。

(1)

式中:δij(i,j=1,2,3)为Xj是单位值时引起的对应于Xi的广义位移;Δip为荷载p引起的对应于Xi的广义位移。

该方程可表示为矩阵方程,如式(2)所示。

(2)

(3)

式中:JS为水平梁截面抗弯系数;JH为垂直梁截面抗弯系数。

(4)

(5)

平行梁端弯矩为:

(6)

式中K=lJH/(HJS)。

当JH比JS大得多时,即K很大,弯矩零点趋于平行梁中心,则有

(7)

式中:εi(i=1,2,3,4)为应变片微应变值;E为弹性模量。

全桥输出电压

(8)

式中:R1=R2=R3=R4=R; ΔRi=R·G·εi(G为应变片的灵敏系数)。

(9)

建立侧摩阻力与输出电压的关系:

(10)

式中:fs为侧摩阻力;α为密封后传感器的修正系数;A为监测装置侧摩阻力感测面面积。

1.2.2 拉压传感器尺寸选择

为了满足大型沉井侧摩阻力监测所需量程,侧摩阻力监测装置最大量程设置为200 kPa,根据侧摩阻力感测面尺寸,拉压传感器所受最大拉压力为980 N。拉压传感器平行梁厚度和长度与梁端应变、最大应力的关系曲线分别如图4和图5所示。由图可知,平行梁的厚度越小、长度越大,弹性元件在荷载作用下微应变越大,即传感器越灵敏,但是最大应力σmax会增大,传感器可能达到屈服状态。为了满足传感器大量程、高精度需求,确定l=14 mm,h=3 mm,b=10 mm,H=19 mm。侧摩阻力监测装置如图6所示。

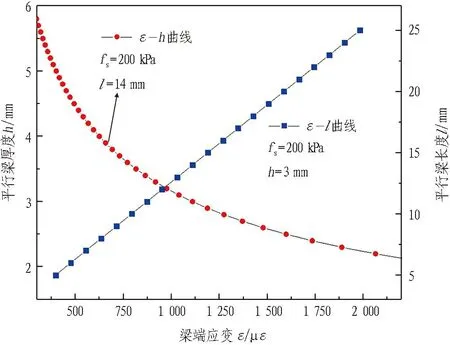
图4 拉压传感器平行梁厚度和长度与梁端应变的关系曲线

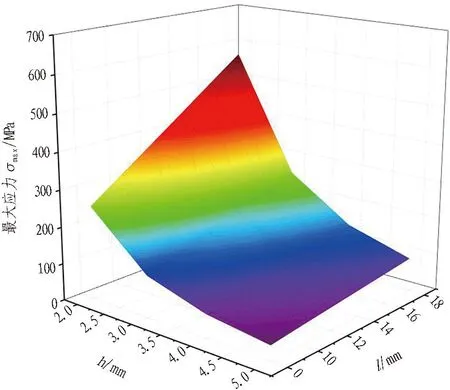
图5 拉压传感器平行梁厚度和长度与最大应力的关系曲线

(a) 内部结构图 (b) 侧摩阻力监测装置

1.3 测试原理

1)在现场监测时,将侧摩阻力传感器埋设于沉井侧壁处,可以根据工程实际情况将其固定于外模或者井壁内钢筋上,待浇筑井壁混凝土后侧摩阻力监测装置与沉井井壁界面平齐,感受侧摩阻力。

2)通过传力体将侧摩阻力传至拉压传感器,由于反力柱约束拉压传感器,导致拉压传感器发生微小弹性变形,引起应变片产生应变,最终引起应变片电阻发生变化。

3)通过解调设备检测的电信号变化解调出对应的侧摩阻力值信号,实现侧摩阻力的测量。

2 密封材料选取

侧摩阻力监测装置经常处于高水土压力环境,为保证侧摩阻力测试结果不受影响,需对传感器进行密封。本文采用有限元软件建立监测装置及密封材料计算模型,研究装置与密封材料组合刚度对传感器应变传递系数的影响。

2.1 模型建立

有限元计算模型如图7所示。传感器中S形测力单元通过反力柱固定在壳体内部,因此弹性体与反力柱均采用固定约束。另外,允许传力体发生切向位移,在传力体底部采用法向约束等效考虑。由于侧摩阻力传递受弹性体和密封材料2种传力介质影响,因此传感器受力特性与密封材料和弹性体的弹性模量比有关(Es/Eg)。其中,传感器弹性体属于弹性结构,采用结构力学来计算弹性体等效模量Eg。为分析不同弹性模量比对传感器应变传递系数的影响,分别对密封材料弹性模量为0.5、1.0、2.0、5.0、10.0 MPa以及传感器未密封时的6种工况进行计算,计算工况如表1所示。

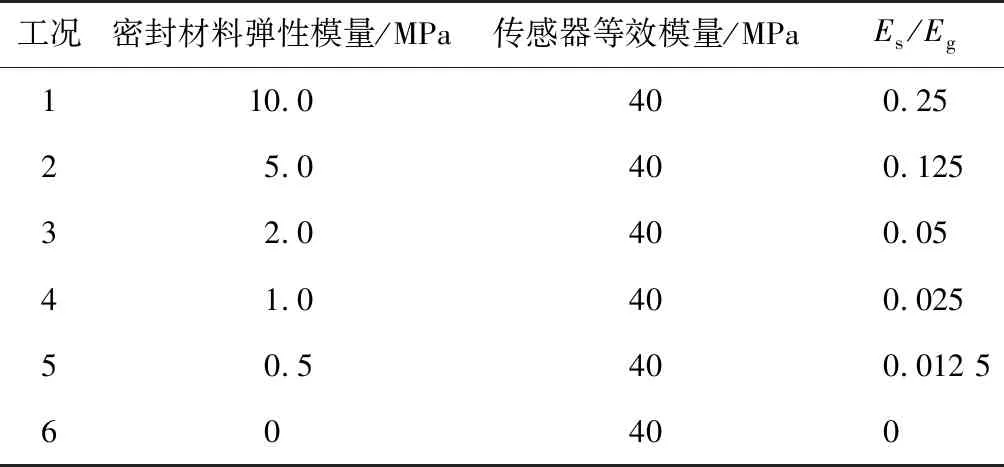
表1 数值计算工况

图7 有限元计算模型

2.2 数值计算结果

密封材料与弹性体弹性模量比与应变的关系曲线如图8所示。由图可知,在没有密封材料时,拉压传感器平行梁端应变为1 336 με,随着密封材料弹性模量的增加,即随着Es/Eg的增加,平行梁端最大应变逐渐减小。当Es/Eg=0.012 5(Es=0.5 MPa)时,平行梁端应变为未密封时应变的90%,即封装后应变损失10%; 当Es/Eg=0.025(Es=1.0 MPa)时,封装后应变损失19%; 当Es/Eg=0.25(Es=10 MPa)时,封装后应变损失达到65%。因此,提升传感器的灵敏度,选择合适的密封材料是关键。

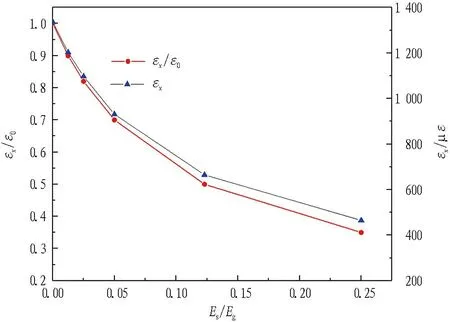
εx为不同密封材料封装后的平行梁端应变; ε0为没有密封材料时的平行梁端应变。

常用的密封材料及参数如表2所示。根据数值计算结果可知: 采用硅酮结构胶密封后应变损失为10%; 采用橡胶密封后应变损失为50%～65%。故选择弹性模量最小的硅酮结构胶作为密封材料,其对传感器灵敏度影响最小。

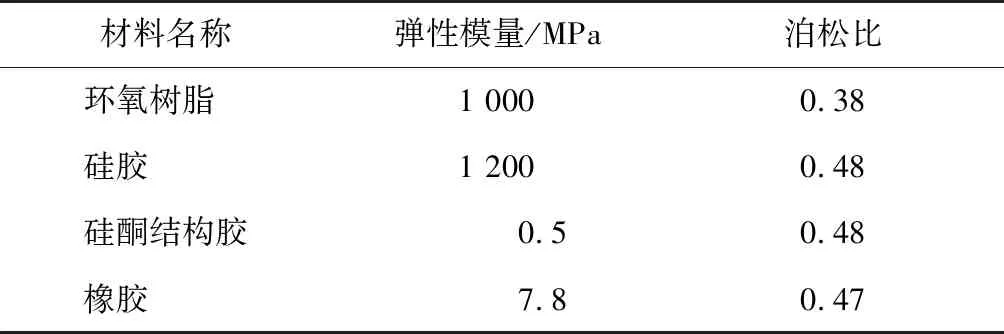
表2 常用的密封材料及参数

2.3 密封材料效果检验

侧摩阻力监测装置采用硅酮结构胶进行密封,如图9所示。

图9 侧摩阻力监测装置密封实物图

为了检验侧摩阻力监测装置的密封效果,采用压力桶对侧摩阻力监测装置密封性能进行试验。将侧摩阻力监测装置浸于压力桶中,采用空压机对压力桶进行增压,使得桶内气压增大至0.7 MPa(等效于70 m水压),在该压力条件下静置1个月。试验结果显示,该装置在高水压条件下可正常监测,具有良好的密封防水性能。

3 侧摩阻力监测装置室内标定试验

3.1 标定装置设计

为验证侧摩阻力监测装置的有效性,在大型直剪仪的基础上进行设计及改装,实现侧摩阻力精准标定,标定系统如图10所示。标定系统由大型直剪仪、大型直剪仪控制系统、变送器、传感器与采集端连接线及侧摩阻力传感器采集软件组成。

图10 侧摩阻力监测装置标定系统

考虑到标定需要验证传感器正压力和侧摩阻力的解耦有效性,采用法向和水平向加载控制系统,利用法向力和水平向力传力机构及侧摩阻力传感器实现法向压力和水平力定量加载,标定系统传力机构如图11所示。加载过程中需要保持剪切力恒定,故采用剪切蠕变模式进行加载。通过大型直剪仪控制系统读取法向加载力和水平向加载力,利用信号采集系统获得传感器电信号,然后以电信号为横坐标,以水平剪切力为纵坐标,进行曲线拟合,得到输出电信号与侧摩阻力的关系,即为侧摩阻力监测装置的标定函数。本次试验分别在法向压力为30、50、100、200、300 kPa的条件下进行3次加载。

图11 标定系统传力机构

3.2 试验结果

不同法向压力加载条件下侧摩阻力监测装置标定曲线如图12所示。

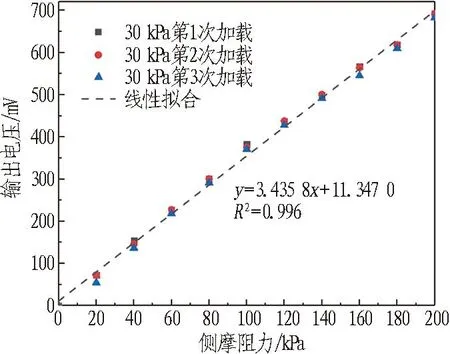
(a) 法向压力30 kPa

由图12可知,侧摩阻力监测装置加载过程表现为明显的线性特性,重复性较好,且不同法向压力加载下曲线的一致性较好,线性拟合系数R2均大于0.99,表现出稳定的传感器特性。法向压力分别为30、50、100、200、300 kPa时监测装置的灵敏系数分别为3.435 8、3.502 4、3.379 5、3.054 2、3.421 5 mV/kPa,说明在不同正压力条件下侧摩阻力监测装置仍具有较好的稳定性,法向压力对侧摩阻力的耦合误差较小。

4 现场应用

4.1 工程概况

哈尔滨某污水处理厂工程1#沉井为顶管接收井,沉井为圆形,直径17 m,井高32.35 m,井壁厚1.5～1.8 m。沉井区域地层分布如表3所示。地下水类型为孔隙潜水,地下水初见水位埋深0.00～0.96 m,静止水位埋深0.00～0.69 m。

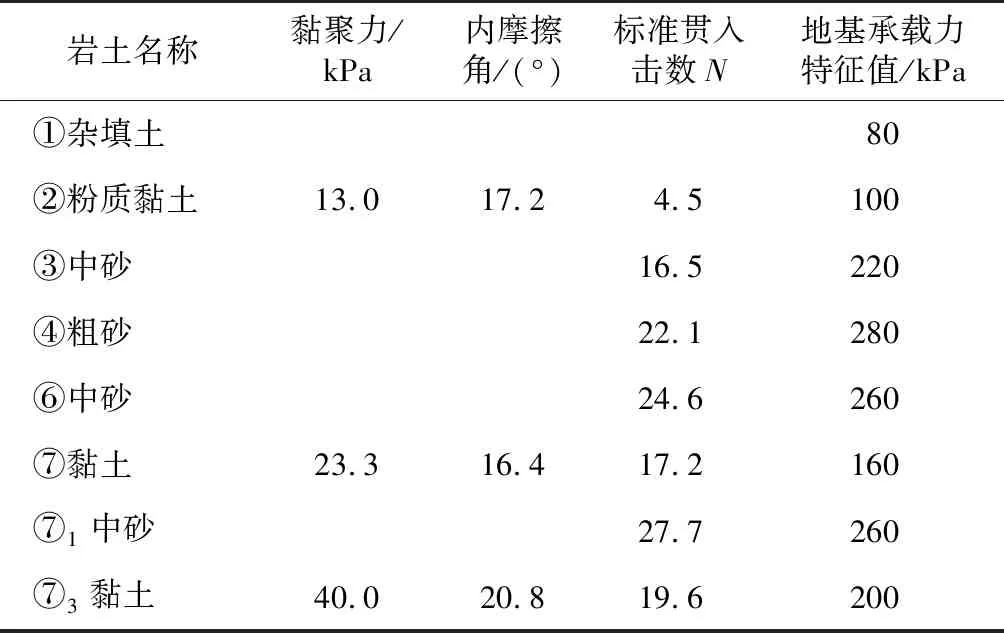
表3 地层分布情况

4.2 传感器安装

沿着沉井壁分别布置3个土压力盒和3个侧摩阻力监测装置,距离沉井刃脚端部分别为1、6、11 m,土压力盒和侧摩阻力监测装置安装在井壁同一高程位置,横向间距为40 cm。监测装置布置示意如图13所示。由于侧摩阻力传感器预埋在沉井外壁,其感测面需与井壁齐平,在下沉前采用水泥砂浆将感测面凹槽填满; 通过布置在井壁内的PVC管将导线引至沉井顶面。现场安装情况如图14所示。

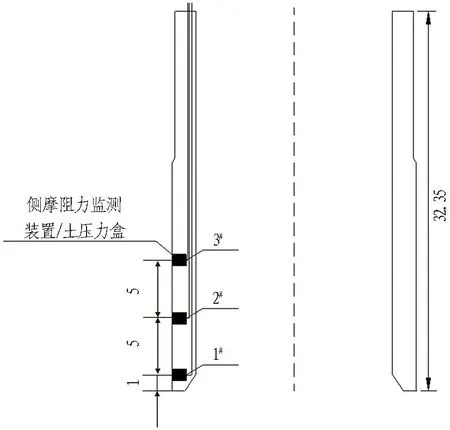
图13 监测装置布置示意图(单位: m)

图14 现场安装情况

4.3 监测结果

4.3.1 侧壁土压力

由现场埋设的土压力盒可以获得沉井侧壁土压力,结果如图15所示。由侧壁土压力实测数据可知,刃脚附近的土压力在下沉前中期整体上随着下沉深度的增加而变大,在下沉后期会出现逐渐减小的趋势; 而离刃脚较远的土压力呈现出一直增大的趋势。侧壁土压力为0～131 kPa。

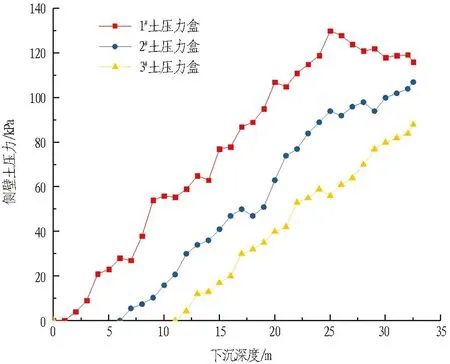
图15 侧壁土压力与下沉深度的关系曲线

4.3.2 侧摩阻力

由现场埋设的侧摩阻力监测装置可以获得沉井侧摩阻力,结果如图16所示。由监测结果可知,沉井侧摩阻力为0～56 kPa,不同下沉深度处侧摩阻力和侧壁土压力的分布规律基本一致,刃脚附近的侧摩阻力随着下沉深度的增加呈现先增大后减小的趋势。这是由于随着沉井下沉深度的增加,刃脚附近土体向井内流动,刃脚附近土压力出现了应力松弛的现象。这与Wang等[16]的研究成果一致。离刃脚较远的井壁侧摩阻力随着沉井下沉深度的增加逐渐增大。由以上分析可知,侧摩阻力监测装置监测结果是合理的。

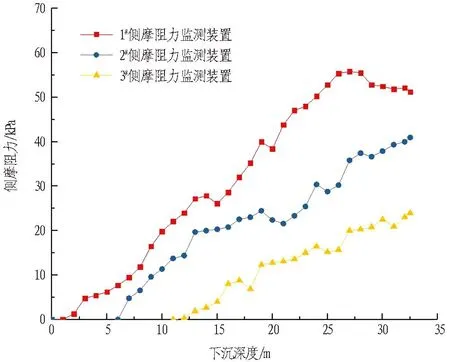
图16 侧摩阻力与下沉深度的关系曲线

5 结论与展望

针对沉井下沉施工过程中侧摩阻力获取难度大、精度低的问题,设计了一种侧摩阻力直接监测装置,并进行现场应用,得到如下结论。

1)通过将拉压传感器简化为闭合框架结构,推导了输出电压与侧摩阻力的理论转化公式,并通过计算分析确定了拉压传感器尺寸。

2)随着密封材料弹性模量的增加,平行梁端最大应变逐渐减小,应变损失逐渐增大。当采用硅酮结构胶进行密封时,应变损失为10%,对传感器灵敏度影响最小。试验表明,监测装置在高水压环境下可正常工作,能够满足工程需求。

3)采用改装的大型直剪仪对侧摩阻力监测装置进行标定,不同法向压力下加载曲线的一致性较好,线性拟合系数均大于0.99,装置稳定性好。

4)随着下沉深度的增加,刃脚附近的侧摩阻力先增大后减小,而离刃脚较远处的井壁侧摩阻力呈现一直增大的趋势,与侧壁土压力的分布规律基本一致,验证了侧摩阻力监测装置监测结果的合理性。

后续可以对侧摩阻力监测装置进行优化设计,进一步缩小其尺寸,扩大应用场景。