基于集对分析理论和数字化平台的山岭隧道塌方风险评价

覃亚伟, 谭 怡, 琚旺来, 陈 斌

(1. 华中科技大学土木与水利工程学院, 湖北 武汉 430074; 2. 武汉华中科大检测科技有限公司, 湖北 武汉 430200; 3. 北京构力科技有限公司武汉研发中心, 湖北 武汉 430223)

0 引言

我国山川广阔,隧道数量众多,随着隧道工程修建经验的积累以及施工技术的不断改进,现代隧道的建设正朝着超长、大跨度、地质环境复杂的方向发展[1-2]。这种趋势增加了施工过程中的不可预见因素和致险因子,加剧了隧道的塌方风险[3-4]。因此,对山岭隧道塌方风险进行准确评价,进一步提高隧道施工安全管理水平尤为重要。

目前,国内外针对隧道风险评估方法的研究已取得了一定的成果,主要有德尔菲法、事故树法、层次分析法、模糊层次分析法、贝叶斯网络法、支持向量机法等。吕擎峰等[5]基于模糊德尔菲法建立隧道施工风险层次模型,得出隧道总体施工风险等级。周小杰等[6]、张楠[7]、詹金武等[8]利用模糊层次分析法,确定指标权重,对隧道施工风险进行评价。南宇宏等[9]利用事故树法,建立隧道塌方事故树模型,对隧道施工塌方事件进行了定性和定量分析。陈钊等[10]结合工程实际,构建隧道塌方贝叶斯网络结构,计算隧道塌方风险等级概率,并进行事故原因诊断。赵雪等[11]建立了基于人工蜂群优化支持向量机回归的隧道塌方风险预测模型。然而,上述研究存在2方面的局限性: 1)主观评价和客观评价没有适当结合。评价方法要么过于依赖专家经验,比较主观;要么需要大量的先验数据,且容易陷入局部最小问题,所确定的边界抗干扰能力差,对噪声和缺失数据敏感。2)当前对隧道施工风险的研究主要集中在对安全影响因素的探讨、评价模型更新和策略建议等方面,对于隧道风险评价和BIM 模型交互的研究较为匮乏,数字化、可视化程度不高。

鉴于此,本文结合主客观综合赋权,运用层次分析法(AHP)和熵值法(Entropy)分别计算2级指标权重,并引入集对分析理论确定指标综合联系度,结合置信度准则对塌方风险的等级进行判定;基于Grasshopper电池组编程模块以及内置的Python二次开发模块,对集对分析理论进行可视化编程程序开发,并将其与隧道-地质BIM交互模型进行耦合,建立基于AHP-Entropy集对分析模型的隧道塌方风险数字化评价平台;最后,结合重庆某隧道实际工程,进行隧道塌方风险评价验证。

1 评价指标体系的建立

通过参考已有山岭隧道评价体系[12-15]并结合工程现场专家经验,将隧道塌方风险因素划分为地质因素、设计因素、施工因素和管理因素,作为塌方风险评价指标体系的准则层;选取12项因素作为塌方风险评价指标体系的指标层,如图1所示。

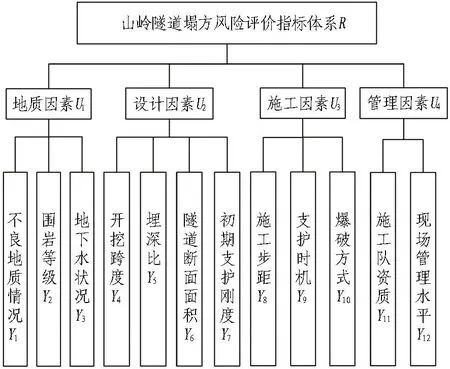
图1 山岭隧道塌方风险评价指标体系

根据《公路隧道风险评价与管理暂行规定》及相关文献研究[16-18],将目标层隧道塌方风险划分为无风险、低风险、中风险、高风险、极高风险5个等级,依次对应Ⅰ—Ⅴ级,并对所有指标进行量化,具体指标分级如表1所示。

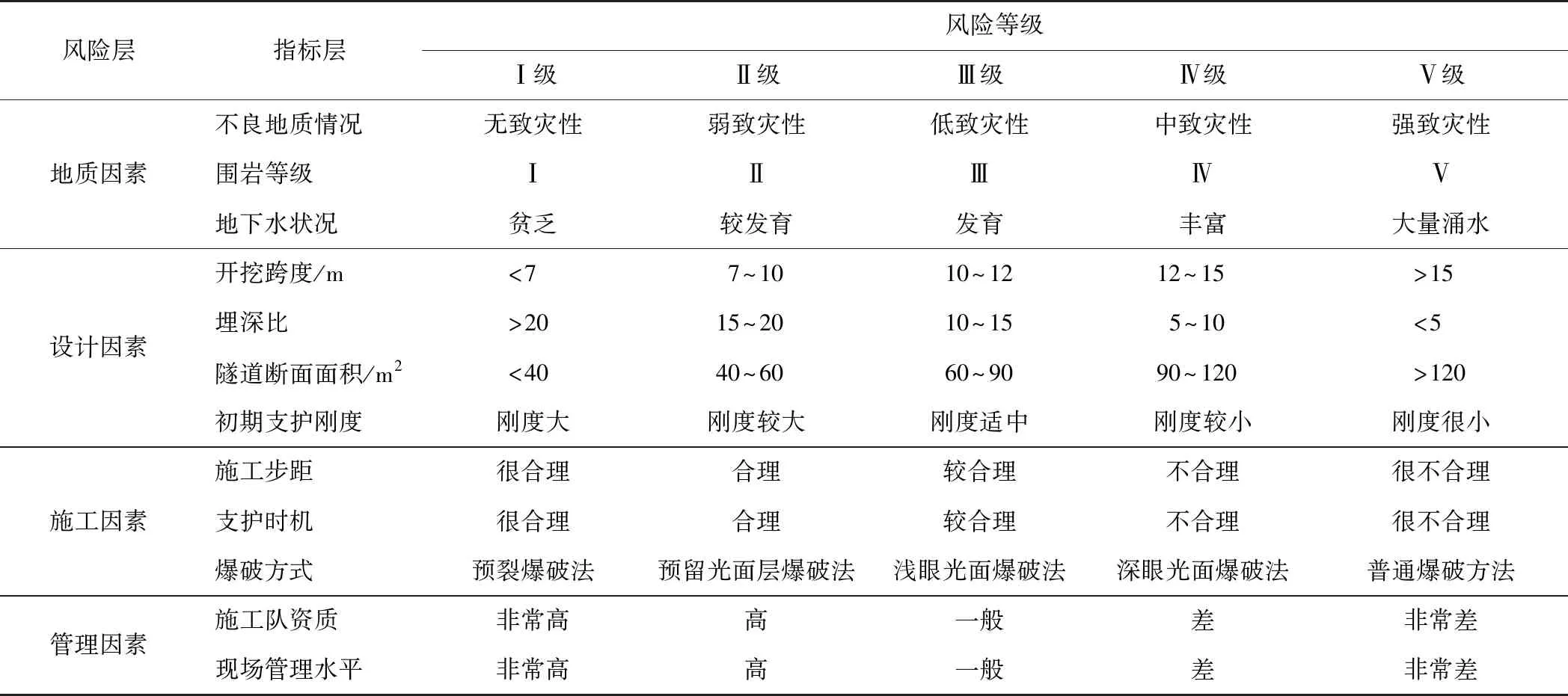
表1 指标等级划分

2 山岭隧道塌方风险集对分析模型

利用AHP-Entropy理论求取指标权重,依据所得权重和集对分析理论,依次确定单指标联系度和多指标综合联系度,最后利用置信度识别准则判别隧道塌方风险等级,从而构建隧道塌方风险评价模型。此外,利用参数化分析软件建立隧道塌方风险评价数字化分析平台。

2.1 基于AHP-Entropy的指标权重

2.1.1 客观权重确定(Entropy法)

熵值法的本质是通过数据熵值的变化来反映该指标的重要程度,数据离散程度越大熵值越小,所包含的信息量越多,从而权重越大。这种方法排除了由于人为评判失误而带来的误差,其熵值Ej计算公式如下。

(1)

式中:m为评价对象个数,本文中为8个隧道区段;ηij用来衡量对象i对指标j的贡献程度,在计算其最小值的过程中会出现ηij=0的情况,此时将存在Ej为无穷的情况,无法进行后续计算。因此,在计算ηij时需要进行修正,修正后的计算公式如下。

(2)

式中bij为对象i的j指标值。

Entropy法最终权重ωj计算公式如下:

(3)

式中n为评价指标数量,本文中为12个评价指标。

2.1.2 主观权重确定(AHP法)

层次分析法是一种主观赋权方法[19-20]。首先,将12项影响因素按照1—9级标度思维方法进行两两比较,构成判断矩阵S,S=(sij)n×n(sij为同层第i个元素与第j个元素的重要性程度,sij∈[1,9]);然后,通过归一化处理得到判断矩阵的特征向量,即每个指标的权重向量P,P=[p1,p2,…,pn];最后,计算判断矩阵的最大特征根λmax和随机一致性比率CR。当随机一致性比率小于0.1时,认为一致性可以接受,即权系数的分配是合理的;否则,需要对判断矩阵进行调整,重新计算。

2.1.3 综合权重计算

Entropy法能够通过熵值的变化发现数据间潜在的联系,但由于缺少主观判断,权重值可能会出现数据失真等与实际不符的情况,而与AHP法相结合能够很好地解决这种问题。复合权重W计算如下:

W=εiωj

。

(4)

式中:εi为一级指标i经过AHP法计算得出的权重;ωj为一级指标i下层二级指标j经过Entropy法计算得出的权重。

2.2 基于集对分析理论的风险综合评价

2.2.1 集对分析理论

隧道塌方风险评价是一个典型的不确定问题,是多因素相互作用的结果。集对分析(set-pair analysis,SPA)理论是一种可以用于定量处理模糊、随机、不确定性问题的数学模型,因此可以用该方法来解决隧道塌方风险的评价问题。集对指的是2个包含不同信息却有一定联系的集合,一般用H=(A,B)来表示。集对的核心是用“相同(identity)”“差异(discrepant)”和“相反(contrary)”3个概念来描述研究对象集对之间的联系状态。

联系度是用来衡量集对H=(A,B)中集合A与集合B之间联系程度(相同、差异、相反)的标准,一般记作μ,其数学模型如式(5)所示。

(5)

式(5)描述的是最基本的三元状态,其集对内部只单独包含一种差异度。而实际工程中2个彼此联系的集合往往有着几种以上不同的差异性质,需要将最基本的三元状态扩展到多元状态,从而更清楚地反映出集对内部的联系状态。多元联系度的数学模型如式(6)所示。

(6)

可简化为:

μ=a+b1i1+b2i2+…+bn-2in-2+cj。

(7)

式(5)—(7)中:N为集对总特征数;S、P分别为集对H=(A,B)内部的相同特征数与相反特征数;F、F1、F2、…、Fn-2为差异特征数;i、i1、i2、…、in-2为其对应的差异程度系数;j为相反程度系数;a、b、b1、b2、…、bn-2、c为各对应特征数与总特征数之比。在隧道施工风险评价中,i1、i2、…、in-2、j的取值没有实际意义,仅作为一种符号用于代表某种风险等级。

2.2.2 模型单指标联系度建立

集对分析理论在隧道塌方风险评价中的应用是一个多元联系的问题,其不仅包含“相同”“差异”和“相反”3种基本状态,而且在“差异”状态中包含多种不同的可能结果。本文将隧道塌方风险Ⅰ级(无风险)定义为“相同”状态;Ⅱ级、Ⅲ级、Ⅳ级定义为“差异状态”;Ⅴ级是最不理想的情况,定义为“相反”状态。结合集对分析原理,单指标Yi的五元联系度μYi的计算公式如式(8)所示。

(8)

式中: 差异程度系数i1、i2、i3以及相反程度系数j分别代表Ⅱ级、Ⅲ级、Ⅳ级、Ⅴ级的风险等级状态;S0—S5分别为表1中Ⅰ—Ⅴ风险等级的界限值;x为当前指标Yi的模型读取值。

2.2.3 模型多指标联系度确定

塌方风险评价是一个多元多指标的复杂综合模型,在单指标联系度求解模型的基础上结合AHP-Entropy权重求解结果,得出综合指标联系度μz的表达式如下:

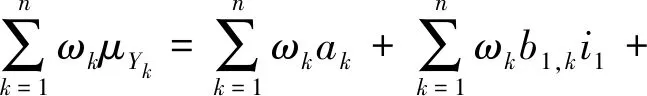
(9)

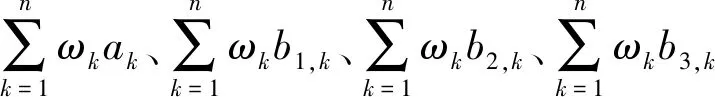
μz=p1+p2i1+p3i2+p4i3+p5j。

(10)

2.2.4 风险评价等级置信度准则判定

在求解出综合指标联系度表达式μz后,用最大隶属度原则来判定隧道塌方风险可能会存在取大运算导致评价结果失真的问题。因此,本文综合考虑各等级概率的影响,引入置信度准则对塌方风险等级进行判定。其判定准则如下。

(11)

式中: 取r=1,2,3,4,5,直至取到满足式(11),则认为待评价风险等级属于r0级别;λ为置信度,取值一般为[0.5,0.7],且越大越偏于保守,本文取λ=0.6[21]。

2.3 数字化分析平台

基于本文建立的风险评价模型和BIM技术,搭建隧道塌方风险评价数字化分析平台。本平台主要是利用隧道模型与地质模型之间的检索、接触等交互操作,实现风险指标体系底层定量指标值的自动抓取;对于定性指标可以利用平台直接读取并保存隧道各区段定性指标评价结果的文本,进而运用集对分析参数化程序自动计算隧道各区段风险等级。数字化分析平台框架示意如图2所示。

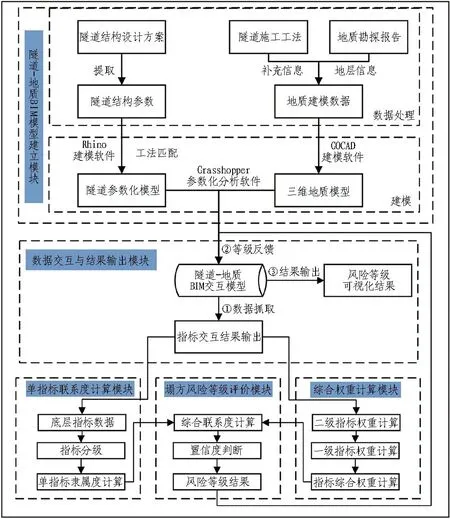
图2 隧道塌方风险评价数字化分析平台框架

数字化分析平台各模块的主要介绍如下:

1) 隧道-地质BIM模型建立模块。该模块基于隧道结构设计方案提取隧道长度、跨度、几何半径等参数,采用参数化建模软件Rhino建立隧道结构参数化模型,并通过额外设计隧道分段长度参数控制风险评价的精细程度。此外,基于隧道施工工法、地质勘探报告,采用SKUA-GOCAD建立三维地质模型,模型中包含地层情况、围岩条件等详细地质信息,并将其导入参数化分析软件中形成隧道-地质BIM交互模型,为后续建立隧道塌方风险评价数字化分析平台以及隧道塌方风险的可视化提供模型数据基础。

2)单指标联系度计算模块、综合权重计算模块以及隧道塌方风险等级评价模块。这3个模块为数字化计算模块,其基于Grasshopper电池组编程模块以及内置的Python二次开发模块,对集对分析理论进行可视化程序开发;并基于风险评价理论的二次开发程序,结合工程数据进行各指标联系度、综合联系度、隶属度的计算,实现了隧道塌方风险全区段精细化求解。

3)数据交互与结果输出模块。该模块利用隧道-地质BIM模型进行数据的自动抓取,并将实际数据与3个计算模块进行交互,实现风险等级的计算和结果可视化输出。该模块利用隧道-地质BIM交互模型自动抓取隧道塌方风险底层指标状态,抓取的参数为隧道塌方风险体系的12个指标值,以埋深比Y5为例,通过计算隧道顶面点集向地表面投影的距离,即可获取隧道埋深情况。将抓取的指标数据输入3个计算模块进行数字化风险评价,获取评价结果;并根据各区段风险等级结果利用不同颜色表示不同的风险等级,将隧道风险等级信息以颜色的形式反馈到隧道-地质BIM交互模型,在对隧道塌方风险精细化评价的基础上实现评价结果的可视化。

3 实例分析

3.1 工程概况

为验证本文所提方法及数字化分析平台的有效性和准确性,以重庆某工程2号隧道右线为背景进行风险评价。该工程2号隧道左线起止桩号为ZK1+986～ZK2+608,全长 622 m;右线起止桩号为YK1+660～YK2+278,全长618 m。隧道限界宽度为17 m,限界高度为5 m,左线隧道为2.75%单向纵坡,右线隧道为2.9%单向纵坡。

该段原为构造剥蚀浅丘地貌,场内上覆土层为第四系全新统素填土、淤泥质粉质黏土、粉质黏土,下伏基岩为侏罗系上统蓬莱组、遂宁组砂质泥岩、砂岩;中统沙溪庙组页岩、砂质泥岩、砂岩;中统新田沟组页岩、灰岩、砂质泥岩、砂岩。勘察区原始地貌为丘陵地貌,地下水主要赋存于场地原始地形谷心地带的覆土层和强风化带岩层中,本工程地下水主要为松散岩类孔隙水、基岩裂隙水,2号隧道洞口范围内无地下水。根据现场勘察以及室内试验可知,2号隧道主要岩土体物理力学参数标准值如表2所示。

表2 2号隧道主要岩土体物理力学参数标准值

3.2 多源数据集成建模

在本次工程中,地质情况较为复杂,存在破碎带等不良地质,根据图2所示的数据处理及建模流程建立隧道-地质BIM交互模型,具体过程如图3所示。

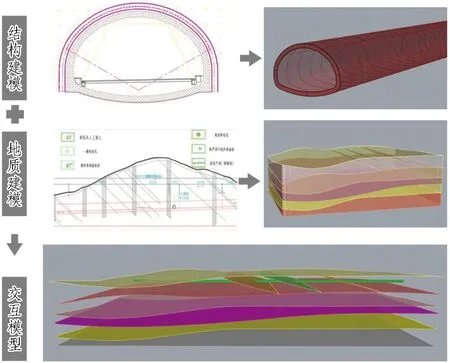
图3 隧道-地质BIM交互模型

3.3 基于数字化分析平台的塌方风险评价

1)指标权重确定。AHP-Entropy法权重计算程序如图4所示。调用图中所示的权重计算模块计算指标权重。首先,将模型参数传入熵值法数学模型,计算各二级指标的熵值并输出;其次,通过专家评分法对隧道塌方风险评价指标体系一级指标进行打分,并输入到AHP计算程序中构建AHP判断矩阵,得到一级指标权重结果,如表3所示。将判断矩阵输入数字化分析平台AHP-Entropy权重计算模块,其输出随机一致性比率CR=0.015 265<0.10,认为该判断矩阵符合一致性检验要求,可以作为隧道塌方风险一级指标权重。最终利用式(4)构建综合权重计算程序。各级指标综合权重计算结果如表4所示。

表3 一级指标权重

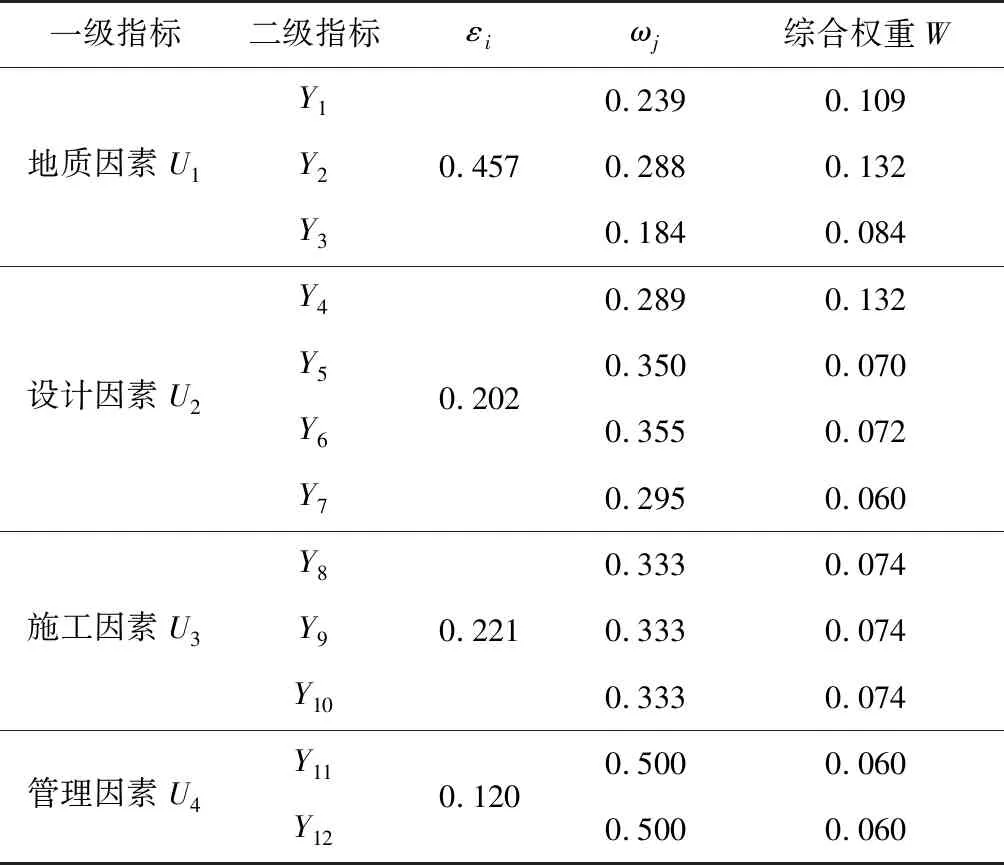
表4 各级指标综合权重计算结果

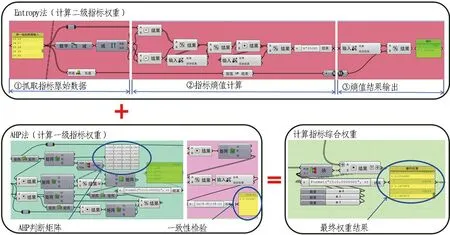
图4 AHP-Entropy法权重计算程序

2)指标数据读取。根据隧道-地质BIM交互模型自动计算定量指标,而对于定性指标需要读取外部输入的数据(Excel文件)进行计算,并按照表1进行打分,转化为数字1～5(代表隶属等级Ⅰ～Ⅴ),结果如表5所示。将表5中的数据接入如图5所示的数字化分析平台,并转换为各指标的数值矩阵,根据读取的各区段隧道长度矩阵值,将对应定性指标数据映射到BIM交互模型中,完成定性指标数据的准备工作。

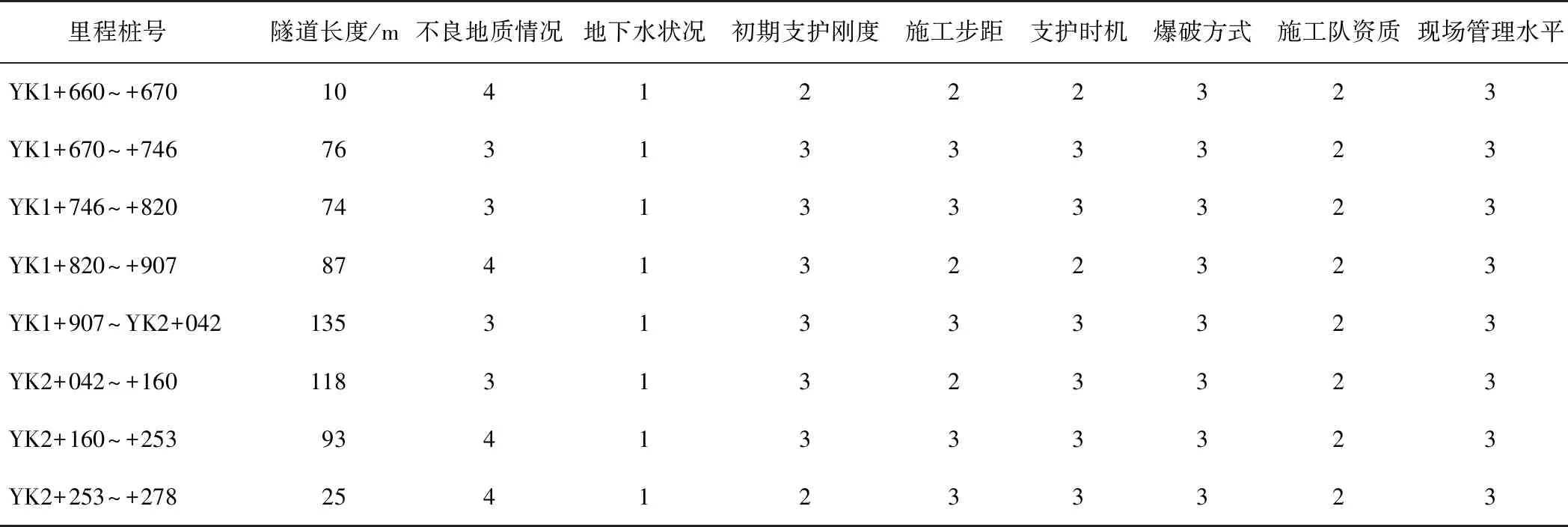
表5 定性指标数据

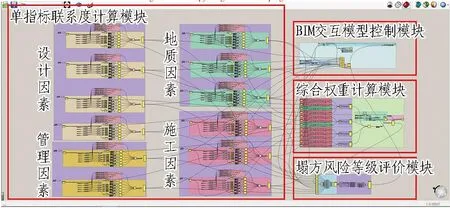
图5 隧道塌方风险评价数字化分析平台界面

3)数字化分析平台计算。利用Grasshopper程序将隧道-地质交互参数化模型接入到平台中完成模型准备工作。模型接入后,数字化分析平台自动抓取风险指标体系各指标值,使用AHP-Entropy集对分析程序自动对各隧道区段数据进行计算。首先,利用模块进行单指标联系度计算;然后,利用求得的综合权重处理单指标联系度系数阵列得到综合联系度;最后,根据置信度准则进行处理,输出各区段塌方风险等级的数值,并进行可视化。

以 K31+799～+809段隧道为例,利用集对分析方法计算各评价指标的单指标联系度,结果如表6所示。计算得综合指标联系度μz=0+0.168i1+0.666i2+0.166i3+0j。

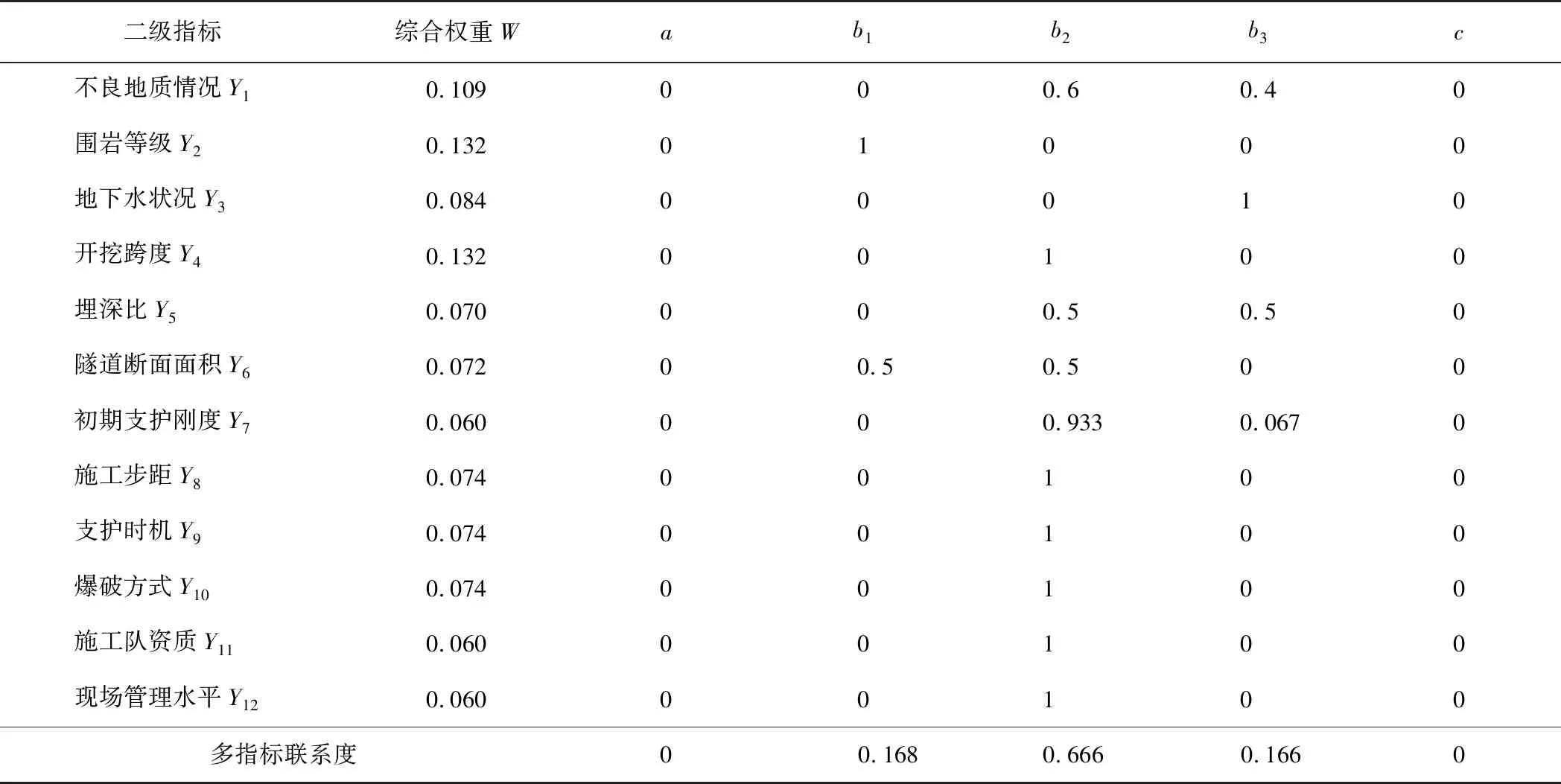
表6 单指标联系度

因为0+0.168+0.666>0.6,根据式(11)可知该段为Ⅲ级风险。

隧道前250 m的区段可视化结果如图6所示,整个平台运行时间约为2 s。由图6可以看出,隧道塌方风险主要以Ⅲ级风险(中风险)为主,属于可接受的风险范围。最高风险等级为Ⅳ级(高风险)主要集中在围岩破碎带,根据隧道风险接受准则可知,Ⅳ级风险为不期望,需要采取风险规避手段降低其风险等级。

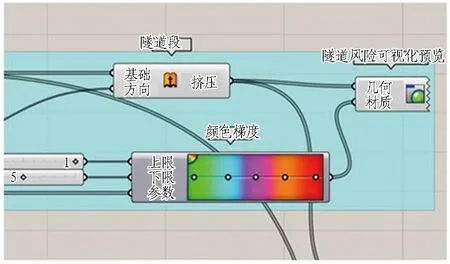
(a) Gradient染色模块

4 结论与展望

1)基于AHP-Entropy法确定评价指标权重,一方面可以减少专家主观因素干扰,另一方面解决了数据失真等与实际不符的问题。将集对分析理论引入山岭隧道塌方风险评价中,较好地解决了评价过程中的多指标和不确定性等问题。

2)将评价方法与数字化分析平台耦合用于重庆某隧道塌方风险评价中,建立隧道-地质模型,在此基础上实现模型与平台的数据交互,利用数字化分析平台各模块间的协作,实现隧道塌方风险的精细化、可视化评价,为山岭隧道塌方风险评价提供参考。

3)在本文建立的数字化分析平台中,用于交互的数据基本为静态数据,未考虑隧道施工的动态过程。在未来的研究中,可以利用动态监测数据、传感器数据等优化数字化分析平台,以进行隧道全生命周期各个阶段的隧道动态风险可视化评价。