基于混合强化学习的主动配电网故障恢复方法

徐 岩，陈嘉岳，马天祥

（1.华北电力大学电气与电子工程学院，保定 071003；2.国网河北省电力有限公司电力科学研究院，石家庄 050021）

配电网连接电网和终端用户，直接影响用户的供电可靠性，如果发生故障，会对用户产生较大的影响。而在配电网自动化故障管理系统中，故障恢复占据重要地位[1-2]。随着经济发展和技术水平提升，对配电网可靠性的要求越来越高，而分布式电源接入比例的提升，也给配电网故障恢复带来了巨大挑战。

配电网故障恢复作为电力系统的重要研究方法，受到了研究人员的广泛关注。目前主要是使用经典算法或智能算法进行恢复。文献[3]采用鲁棒优化理论建立故障恢复方法，将风光出力和故障恢复方案分别作为自然决策者和系统决策者，令两者进行博弈，具有较好的鲁棒性；文献[4]利用网络拓扑分层划分特定网络的自愈单元组，再根据自愈单元的基本环路矩阵确定非故障失电区范围和复电方式，显著减少了拓扑遍历的复杂度，加快了运算速度；文献[5]提出了一种基于生物体免疫机制的故障恢复方法，通过模拟生物体对外部微生物的免疫行为，能快速获得恢复方案，对配电网故障进行有效恢复，这种方法在分布式电源接入的情况下有显著优势；文献[6]使用二进制粒子群算法对交直流混合配电网故障进行恢复，对所建立的模型设计两阶段优化求解流程，能有效降低求解难度、提高求解效率。

强化学习作为一种新兴的机器学习方法，近年来受到了广泛关注。不同于监督学习和非监督学习，强化学习不需要事先给定数据，而是通过智能体接受环境反馈，并利用反馈学习信息更新模型参数。目前，已有学者使用强化学习方法来解决电力系统相关问题。针对故障检测和恢复问题，也有学者提出了相关解决方法。文献[7]通过提取孤岛微电网的故障特征，基于深度强化学习方法，深度跟踪电网故障信息，通过三端行波测距法，判定孤岛微电网故障区域；文献[8]把恢复问题转化为一个顺序决策问题，在电源侧和负载侧实现了双重最优控制策略，提高了系统的恢复能力；文献[9]提出了一种基于改进深度确定性策略梯度DDPG（deep deterministic policy gradient）算法的服务恢复方法，来辅助孤岛微电网的服务恢复，该方法能可靠收敛，学习性能较高。但目前已有研究较少涉及主动配电网的故障恢复，同时针对高比例新能源配电网，故障恢复时较少考虑分布式电源的调控问题。

基于此，本文提出一种基于混合强化学习的主动配电网故障恢复方法。将配电网故障恢复问题转化为规划问题，以故障损失最小为目标、电网安全运行条件为约束，建立马尔可夫模型，构建智能体和配电网交互环境。恢复模型中动作空间既有离散动作又有连续动作，现有方法是将连续动作转化为离散动作，再进行处理，该方法会增加恢复过程的计算量，减慢恢复速度。因此，本文将竞争架构双深度Q 网络D3QN（dueling double deep Q network）和DDPG算法进行混合，使用D3QN算法处理离散部分、DDPG算法处理连续部分，很好地解决了计算量大、恢复速度慢的问题。通过仿真实验验证了本文方法比传统算法或单一强化学习算法能显著减少恢复时间，提升恢复效果。

1 主动配电网故障恢复模型

在配电网故障发生时，应尽可能使损失最小，并将停电对用户的影响降到最低。故障恢复过程中，应保证各项参数在允许范围内，确保配电网安全有序恢复。本文由此构造目标函数和约束条件，建立恢复模型。

1.1 目标函数

以故障综合损失最小为目标，构建主动配电网恢复模型，定义恢复目标函数为

式中：g1为总失电负荷；g2为开关动作次数；g3为恢复成本；g4为网络损耗；g5为电压波动；g6为用户总停电时长；k1、k2、k3、k4、k5、k6分别为子函数对应的权重；g1、g2、g3为恢复效果目标；g4、g5、g6为电能质量目标。g1、g2、g3、g4、g5、g6可分别表示为

式中：ωi为节点i的负荷重要度系数；Di,t为节点i在t时刻的负荷时变需求系数；Li,t为节点i在t时刻负荷需求量；N为节点总数；xi,t和si,t分别为节点和支路的接入状态，其为0-1变量，当取值为1时表示节点或支路接入；Δsi,t=si,t-si,t-1；cG、cDESS、cPV、cWT分别为火电机组、储能设备、分布式光伏和风电机组的运行成本；NG、NDESS、NPV、NWT分别为配电网中火电机组、储能设备、分布式光伏和风电机组的数量；T为故障恢复总时间；M为支路集合；Rs为支路s的阻抗；Ps、Qs、Us分别为支路s末端节点的有功功率、无功功率和电压幅值；为节点i在t时刻的电压幅值；为节点i的电压额定幅值；α为停电时间损失系数，取a>1。

1.2 约束条件

本文模型考虑潮流约束、储能约束、分布式电源约束和恢复时间约束。运行的电力系统应满足基本的有功功率和无功功率平衡约束，即

式中：Pi,t、Qi,t分别为t时刻节点i流入的有功、无功功率；、分别为t时刻节点i发电机有功、无功功率；、分别为t时刻节点i储能装置的充、放电功率；、分别为t时刻节点i光伏设备的有功、无功输出；、分别为t时刻节点i风力发电机的有功、无功输出；、分别为t时刻节点i负荷消耗的有功、无功功率。

故障恢复过程中，为保证电能质量，配电网各节点电压和功率不应超出允许的最大范围，即

式中：Ui,t为t时刻节点i处的电压；Ui_min和Ui_max为节点i处的电压下限和上限；Pi_min、Pi_max、Qi_min、Qi_max分别为节点i处的有功功率和无功功率的下限和上限。

储能设备工作时，应满足如下功率约束条件：

式中：为t时刻节点i储能设备的总功率；ηDESS为储能设备的充放电效率；和分别为储能设备总功率的下限和上限；和分别为充电功率的下限和上限；和分别为放电功率的下限和上限。

同时，储能设备应满足如下容量约束条件：

式中：为t时刻节点i储能设备的容量，kW·h；和分别为储能设备容量的下限和上限。

新能源配电网通常有高比例分布式电源接入，接入的分布式光伏电站和风力发电机组应满足如下约束条件：

式中：η为光电转化效率；APV为光伏组件受光面积；I为辐照强度；vt为t时刻的风速；vci、vfi、vrate分别为风电机组的切入、切出、额定风速；b1、b2为常系数；Pr为风电机组额定功率；为光伏设备的最大有功功率；为风电机组的最大有功功率。

为确保终端用户的供电质量，需要对恢复时长进行约束。设用户可接受的最大停电时长为Tmax，则恢复时间T应满足

配电网恢复过程应充分考虑以上约束条件。以式（11）为目标函数、式（8）～（22）为约束条件，将主动配电网故障恢复问题构建为一个混合整数二次规划MIQP（mixed integer quadratic programming）问题。

2 用于配电网恢复的强化学习过程

强化学习的本质是构建一个智能体，令智能体和环境进行交互。在这一过程中，智能体会得到环境的反馈，并通过反馈调整下一步的动作，进而完成对环境的最优响应。强化学习解决的实际问题规模较大，在解决问题过程中，通常假设状态转化过程具有马尔可夫性，故这种决策过程被称为马尔科夫决策过程。该决策过程可把配电网故障恢复问题拆分成一系列单阶段问题进行求解。马尔可夫决策过程可以描述为五元组形式，即

式中：S为状态空间，st为状态空间集中的某一个状态；A为动作空间，at为动作空间集中某一个动作；R为环境奖励，rt为其中某一个奖励；γ为奖励衰减因子，表示当前延时奖励和后续状态奖励之间的权重关系，γ∈[0,1]；π为个体策略，表示个体采取动作的依据，即个体会依据策略概率π来选择动作。通常采用条件概率分布π(a|s)=p(A=at|S=st)来表示个体策略，即在状态st时采取动作at的概率。

在智能体和环境的交互过程中，智能体会根据t时刻环境状态st、接收奖励rt及个体策略π来选择合适的动作at；然后将环境状态从st转换到st+1，智能体获得动作at的延时奖励rt+1=r(st,at,st+1)。马尔可夫决策过程如图1所示。

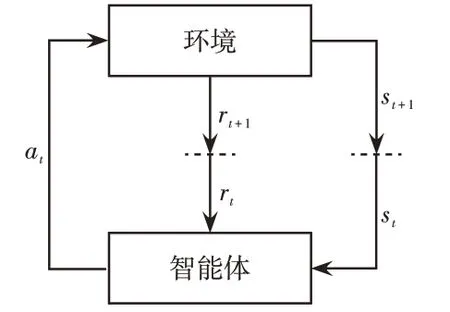
图1 马尔可夫决策过程Fig.1 Markov decision process

在马尔可夫决策过程中，智能体会通过迭代学习过程获得决策能力，决策目标为给定状态和动作(s,a)时，动作价值函数Qπ(s,a)的期望值最大，即

式中：Eπ为智能体依据π选择动作at所获得的期望价值函数；RT为截至到T时刻累计的奖励总和。

2.1 用于故障恢复的强化学习模型

根据第1 节所述的目标函数和约束条件，构建配电网恢复问题的马尔可夫模型。

2.1.1 动作空间

配电网故障恢复过程中，需要同时操作断路器和调节电源出力。断路器的状态只有打开和闭合两种状态且动作空间离散，而电源出力是一个连续调节的过程且动作空间连续。因此，分别将这两个动作空间记为Ad和Ac，即

设断路器t时刻的动作为0-1 状态变量os，其中os=0 表示未对断路器进行操作，保持t-1 时刻状态；os=1 表示对断路器进行操作，与t-1 时刻开关状态相反。将离散状态空间Ad用os表示，即

式中：Np为配电网中可操作断路器的数量；os,i为第i个断路器的动作状态；τ为断路器集合。

将恢复过程的电源出力以连续状态表示，即

式中：Nq为配电网中可控电源的数量；Ps,i和Qs,i分别为节点i处可控电源的有功和无功功率；σ为可控电源集合。

2.1.2 状态空间

在配电网模型中，任意时刻系统的状态S可由系统观测状态和系统运行约束两部分组成。分别构建观测状态空间SO和约束状态空间SC，即

在配电网运行时，若配电网的约束条件不变，则状态空间可以简化为SO，而SC作为已知常量输入智能体。

2.1.3 奖励空间

奖励函数的设计直接影响智能体的决策，设计过程中需充分考虑目标函数和约束条件。智能体在动作集A中选择任一动作后，环境会根据智能体的完成情况给予不同的奖励值。在本文中，若配电网故障得到恢复，则智能体获得正向奖励；反之，若故障恢复失败，则对智能体进行惩罚。

由于配电网不同约束条件对应不同的重要程度，设置惩罚函数包括软约束惩罚和硬约束惩罚，则奖励函数和惩罚函数分别为

式中：rk1为奖励函数；rk2和rk3分别为软约束惩罚和硬约束惩罚；N1为收到奖励的动作数；N2和N3分别为收到软约束惩罚和硬约束惩罚的动作数；ξ0、ξ1、ξ2为奖惩常数，可根据电网恢复需求设定；ξ′为很大的惩罚系数，代表违反硬约束的惩罚；ai为智能体动作；k1、k2、k3为智能体所属的动作空间；ci为常系数。这里软约束条件可以被突破，智能体会被施加惩罚；而若硬约束条件被违反，则恢复过程终止。

2.2 混合强化学习算法

由式（26）～（31）可知，本文拟解决的问题为状态空间连续且动作空间兼具离散与连续的混合问题。目前，常用的解决方法是将动作空间中连续部分转换成离散部分，使用深度Q网络DQN（deep Q-learning network）等算法加以求解，但会增加计算量，减慢计算速度。为解决此问题，本文提出了一种混合强化学习算法，将D3QN和DDPG算法相结合，使用D3QN 算法处理动作空间离散部分，DDPG 算法处理动作空间连续部分，达到精简动作空间的目的。

2.2.1 双深度Q 网络

Q-learning方法是一种常用的强化学习方法，适用于解决配电网中离散变量的决策问题，是一种广泛应用的强化学习方法。此方法根据当前状态st由智能体决策得到动作at。Q值函数可以表示为

式中：μ为折扣因子；st和ad,t分别为t时刻状态值和离散动作值；Q(st,ad,t)为当前状态和动作对应的Q 值；Q′(st,ad,t)为上次迭代获得的Q 值；r(st,ad,t)为智能体在当前状态和动作获得的奖励。为解决高维度运算存在的内存溢出问题，采用神经网络逼近Q值的DQN算法。

在DQN算法中，定义Q值函数为

式中，θ为神经网络的训练权值。DQN有两个结构相同的神经网络，其中一个用于计算目标Q 值，另一个用于估计当前状态的Q 值。DQN 算法的目标是训练合适的权重，使得目标Q值相对于当前状态Q值的损失最小化。yd,t为DQN算法中离散动作目标网络的Q值，可表示为

式中，θ′为目标网络的权值。

DQN算法普遍存在高估问题，会导致训练结果偏离期望值。为解决这一问题，文献[10]提出了Double DQN算法，对目标网络的动作选择和评估进行解耦，从估计网络中选择Q值最大的动作。Double DQN 与DQN 算法的区别仅在于目标Q 值的计算。Double DQN 算法中离散动作目标网络的Q 值可表示为

为了保证动作选择在特定状态下的支配性，文献[11]提出了Dueling DQN 算法。Dueling 网络的结构如图2 所示。Dueling 神经网络的状态输出为状态值函数V(st)和动作优势度函数A(st,ad,t)的组合，然后将两者耦合到每个动作的Q 值函数。此时Q值函数可以表示为

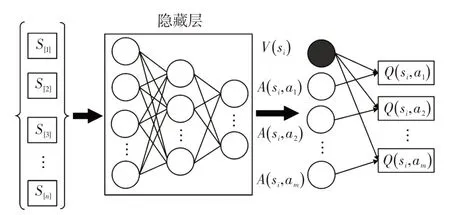
图2 Dueling 神经网络结构Fig.2 Structure of dueling neural network

式中：|A|为可执行动作的数量；为动作优势度函数中的离散动作值。

D3QN 算法在Double DQN 的基础上改进了网络结构，其余部分并无差异。在将D3QN 算法应用于故障恢复模型时，V(st)仅与配电网状态有关，A(st,ad,t)与配电网状态和断路器动作状态有关。这种处理减少了训练中错误动作对Q值计算的影响，能有效提升收敛速度。

2.2.2 深度确定性策略梯度

DDPG 是一种基于行动者-批评家架构的强化学习算法，适用于解决配电网中连续变量的决策问题，本文使用DDPG 算法来调节各节点上的电源功率。在DDPG 算法中，使用两个网络对智能体进行训练，行动者估计网络β用来近似策略函数，神经网络参数为θβ；批评家估计网络ψ用于评价当前状态下动作效果，神经网络参数为θψ。为了提高训练的稳定性和收敛性，DDPG 算法还引入了行动者目标网络β′和批评家目标网络ψ′，对应的参数分别为θβ′和θψ′。

行动者估计网络参数θβ的更新是沿着使Q 值更大的方向进行的，即

式中：∇θJ为在优化目标函数J中对θ的梯度；∇acQ和∇θββ分别为对θψ和θβ的梯度；ac为连续动作值。

批评家估计网络参数θψ使用最小化损失函数来更新，即

式中：yc,t为连续动作目标网络的Q值；ac,t为第t次循环对应的连续动作值；rc,t为第t次循环连续动作获得的奖励值。

2.2.3 基于混合强化学习的恢复方法

本文提出的混合强化学习算法采用D3QN 控制离散动作、DDPG控制连续动作，来实现故障的快速恢复。两种算法在训练过程中独立与环境交互，并从环境中更新同一状态，当其中一个算法在训练时，将另一个算法参数固定，作为训练环境的一部分。本文提出的算法流程如图3 所示。其中，ad,i和ac,i分别为数组中第i个离散动作和连续动作，rd,i和rc,i分别为数组中第i个离散动作奖励值和连续动作奖励值。

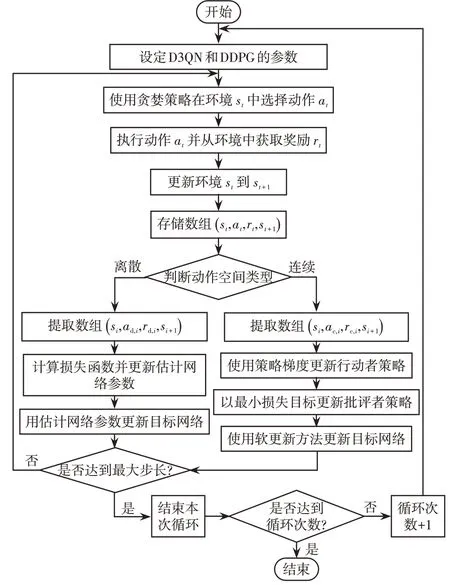
图3 混合强化学习算法流程Fig.3 Flow chart of hybrid reinforcement learning algorithm

以图3所示的流程在给定的配电网拓扑结构中进行训练，训练完成的智能体可用于配电网故障恢复。

3 算例分析

通过IEEE33节点配电网系统，验证本文算法的有效性。本文计算机配置为Intel Core i5-1130 CPU，16 GB RAM，软件采用python 3.10.6。分别使用D3QN算法、DQN+DDPG混合算法、D3QN+DDPG混合算法（本文算法）及传统粒子群算法对系统进行故障恢复。

仿真所用IEEE33节点配电网如图4所示，首段基准电压取12.66 kV，在节点12和节点23节点接入分布式光伏，节点7接入风电机，节点29接入储能装置。

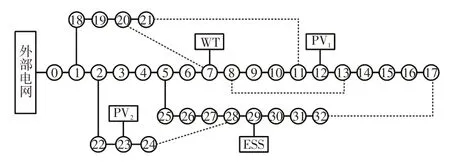
图4 算例用IEEE33 节点配电网示意Fig.4 Schematic of IEEE33-node distribution network in example

3.1 模型训练

模型训练过程中的相关参数设置如表1 所示。训练奖励-步长曲线如图5所示。由图5可知，3 种算法均能有效收敛，其中本文算法比D3QN 算法收敛速度更快，比DQN+DDPG 算法在收敛稳定性上更具优势。这表明Double DQN 和Dueling network的引入能提升收敛稳定性，本文算法在训练效果上优于其他强化学习方法。

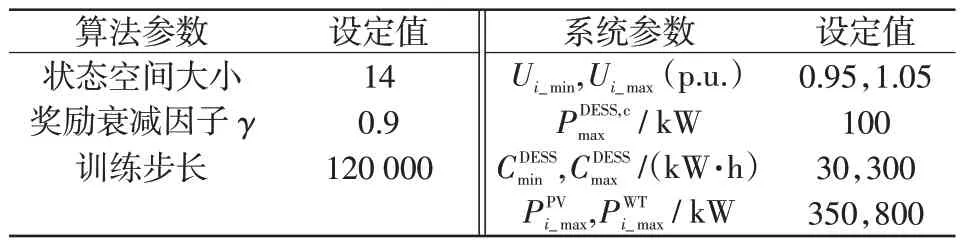
表1 算例参数设置Tab.1 Parameter setting for example

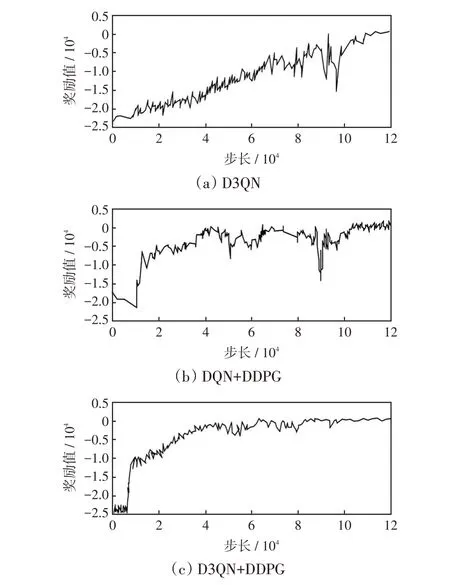
图5 训练奖励-步长曲线Fig.5 Curve of training reward vs step length

3.2 恢复效果

将训练好的模型进行保存，并对IEEE33节点配电网进行恢复，分别设定4种情况的仿真参数如下。情况1：恢复步长为20、离散变量数为420、连续变量数为400；情况2：恢复步长为40、离散变量数为840、连续变量数为800；情况3：恢复步长为60、离散变量数为1 260、连续变量数为1 200；情况4：恢复步长为80、离散变量数为1 680、连续变量数为1 600。将本文算法与D3QN 算法、DQN+DDPG 混合算法、粒子群算法进行对比，恢复效果如图6和表2所示。

表2 恢复效果对比Tab.2 Comparison of recovery result

图6 恢复过程相关参数Fig.6 Related parameters of recovery process

图6 给出了恢复过程失负荷量、网络损耗、储能装置功率、光伏功率和风机功率的变化情况。可以看出，对于失负荷量，本文算法的曲线前段下降迅速，在恢复速度上优于其他算法，同时3 种强化学习算法恢复后的失负荷量均优于粒子群算法，其中本文算法略优于D3QN算法和DQN+DDPG算法；对于网络损耗，本文算法优于DQN+DDPG 算法和粒子群算法，这是因为D3QN 算法在网络损耗控制方面表现更好，降低了恢复过程的网络损耗；对于储能装置功率，本文算法中储能装置的平均功率最小，功率波动平缓，有些时段还可利用盈余功率进行充电，这样可有效减少储能设备的装机容量，延长装置寿命，降低装设成本；对于光伏和风机功率，本文算法中光伏和风机的平均功率高于其他算法，功率曲线更为平缓，这表明本文算法在分布式电源调控方面具有优势。

表2给出了恢复过程中4种算法的最优目标函数值和恢复时间的对比。可以看出，对于最优目标函数值，4 种仿真情况下本文算法的最优目标函数值均最小，恢复效果最优，而且随着离散变量和连续变量数量及步长的增加，本文算法的恢复效果的优势更为明显。此外，3 种强化学习算法的恢复效果均优于粒子群算法且优势明显。对于恢复时间，3种强化学习算法的恢复速度均明显优于粒子群算法，这是因为强化学习算法在训练完成后，保存的智能体可以直接用于恢复，在同一拓扑结构下无需重新训练。本文算法的恢复时间最短，同时随着离散变量和连续变量数量及步长的增加，几乎没有造成恢复时间的延长。而粒子群算法随着离散变量和连续变量数量及步长的增加，恢复时间会明显延长，在步长为80 时粒子群算法恢复时间是本文算法的2 300倍。上述结果验证了本文算法在恢复速度方面也优于传统算法。

4 结 论

本文提出了一种基于混合强化学习的主动配电网故障恢复方法，主要结论如下。

（1）本文针对主动配电网故障恢复问题，构建了配电网故障恢复模型，同时模型中还考虑了高比例新能源接入的情况。

（2）选取D3QN+DDPG 混合算法作为训练算法，解决了传统强化学习方法只能处理单一动作空间的问题。结果表明，本文算法在训练时收敛稳定性高，恢复过程网络损耗控制良好，分布式电源出力平稳，对储能装置依赖也较小，同时在恢复速度和恢复效果上优势明显，验证了本文算法的有效性和优越性。