基于SEPIC 的新型高增益DC-DC 变换器及衍生拓扑分析

魏业文，李 明，李俊波，宁鑫淼，白文静

（1.三峡大学电气与新能源学院，宜昌 443002；2.三峡大学智慧能源技术湖北省工程研究中心，宜昌 443002）

近年来，由于对环境的日益关注、可再生能源基础设施成本的降低以及其技术的进步，全球可再生能源的发电能力大幅提高。在这种背景下，电力电子技术的升级至关重要[1]。电力电子变换器通常用于可再生能源系统中，以调节可再生电源的输出电压。然而，由于光伏组件的输出电压较低（20～40 V），需要高升压DC-DC 变换器将光伏系统的低直流电压提升至400 V，然后通过功率逆变器将其转换为交流电压[2-3]。

传统的Boost变换器由于其操作简单和元件数量低而被广泛应用。理论上，它的电压增益可以从1（占空比为0）扩展到无穷大（占空比为1）。然而，当其以较高的占空比运行时，由于寄生元件的存在，其电压增益会急剧下降。此外，其半导体器件上的电压应力很高，等于输出电压[4]。为了克服其上述缺点，国内外学者提出了各种变换器拓扑结构，包括开关元件技术（开关电感和开关电容）、级联技术（输出串联和变换器串联）和磁耦合技术[5-9]。除上述传统升压技术，研究人员提出了多种新型升压结构。文献[10]提出了一种电容箝位型双开关高增益DC-DC变换器，将电容箝位结构应用在交错并联结构上，推导出4类新型高增益DC-DC变换器。尽管实现了高电压增益和低电流纹波，但其功率器件的电压应力箝位于输出电压的2/3处。文献[11-12]分别在Boost 变换器的输出端和输入端添加了电感-电容-二极管L-C-D（inductance-capacitance-diode）升压网络，尽管降低了半导体器件的电压应力，但增益提升有限。文献[12]在输入端分接了电容元件，造成输入电流纹波相对较高。文献[13]提出了一族具有零纹波结构的有源开关电感升压变换器，实现了输入电流的零纹波，但其功率器件电压应力较高，且使用了额外的有源开关。

单端初级电感变换器SEPIC（single ended primary inductor converter）具有输入电流连续和输入输出电压同极性的优点，得到了广泛的应用。文献[14]介绍了一种改进型的SEPIC变换器，将SEPIC的第二电感器用电感-电容L-C（inductance-capacitance）网络代替，但其电压增益并未得到有效提升。文献[15]提出了一种新型的SEPIC 变换器，在其输出端添加了L-C-D 升压网络，在提升SEPIC 变换器的电压增益的同时降低了半导体器件的电压应力。文献[16-17]提出了两种增强增益型SEPIC变换器，通过增加额外的开关-电感升压回路以提升电压增益，但使用两个开关，控制复杂度高，且输入电流纹波大。此外，文献[18-21]中将耦合电感集成SEPIC转换器中，利用隔离变压器和耦合电感技术来实现高电压增益，但存储在磁耦合元件漏电感中的能量可能会导致功率开关两端的高电压尖峰、高开关损耗。

综上所述，这些变换器存在的共同问题是电压增益普遍低且半导体器件上承受了较高的电压应力，限制了高增益变换器效率和成本的进一步优化。为解决上述问题，本文提出了一类外部升压型高增益DC-DC变换器，所提变换器利用阻抗网络和开关电容网络组成的外部网络实现了高电压增益和低半导体器件应力，同时保留了原变换器连续输入电流的优势并降低了输入电流纹波。以SEPIC变换器为基础，对构成的变换器各模式下的原理和特性进行了分析，并就电压增益和半导体器件电压应力关系与其他变换器做了对比研究。另外给出了利用所提外部网络构成的衍生拓扑，并对其进行了分析和仿真验证。最后，通过一台200 W的实验样机，验证了理论分析的正确性。

1 稳态工作原理

1.1 变换器拓扑结构及稳态假设

如图1（a）所示，为了实现更高的电压增益，本文首先在文献[15]所提变换器基础上添加了开关电容单元，形成如图1（b）所示拓扑结构。

图1 所提变换器拓扑结构推导过程Fig.1 Derivation process of the topology of proposed converter

由于电容C1、C3和C5在各个模态的充放电工作方式一致，进一步将电容图1（b）中所示L-C-D升压单元的C1、C3和C5采用串联方式连接，升压单元被改造成为阻抗网络。流过C4的电流IC4，会途径CS流入b点，因此可以将电容C4的a点与b点直接相连接，推导出本文拓扑结构，如图1（c）所示。

为了更加直观表示各个单元，将电路图改画，形成本文所提拓扑结构，如图2所示。所提变换器拓扑由1个功率开关( S1) 、5个二极管(D1～D5)、4个电感(L1～L4)、8个电容器（C1～C7和CS）组成，Vin表示直流输入源，R表示负载。可以将其分为内外两部分，阻抗网络（L2、L3、C2、C3和D2）和开关电容（C5～C7和D3～D5）网络共同构成了所提变换器的外部，内部电路为基本SEPIC变换器的输入级（L1、L2、S1和CS），外部网络增强了SEPIC 变换器的电压增益，并使得半导体器件上的电压应力显著降低，同时保留了低的输入电流纹波。

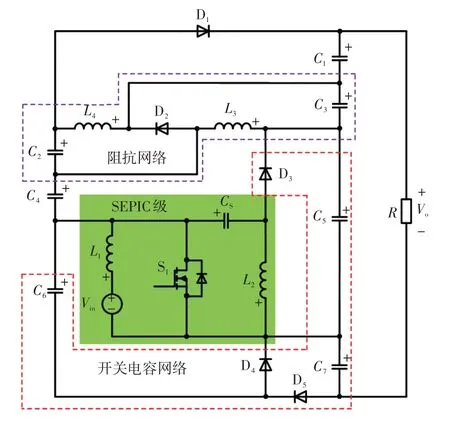
图2 所提变换器拓扑结构Fig.2 Topology of proposed converter

为便于对所提变换器进分析，做如下假设：

（1）忽略功率MOSFET 的导通电阻ron、二极管的导通压降VFD和导通电阻rD；

（2）电感和电容均为理想元件，即忽略电感元件和电容元件的等效串联电阻ESR（equivalent series resistance）rL、rC；

（3）所提变换器的电容和电感都足够大，因此假设电容电压和电感电流是恒定的。

1.2 开关模态分析

1.2.1 连续导通模式分析

所提变换器工作在连续导通模式CCM（continuous conduction mode）和断续导通模式DCM（discontinuous conduction mode）时主要工作波形如图3所示。从图3（a）可以看出，CCM下变换器有2种工作模态。模态1 的时间为DTS，模态2 的时间为(1-D)TS，其中TS为开关周期，D是占空比，Vin和Vo是输入和输出电压，VGS为功率开关触发脉冲幅值。

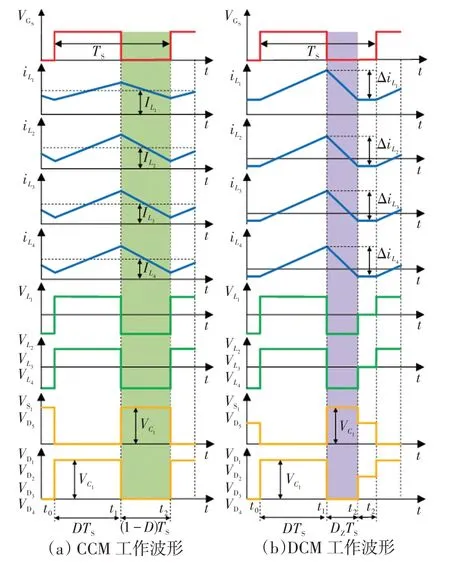
图3 所提变换器的主要工作波形Fig.3 Main working waveforms of proposed converter

1）模态1

[t0～t1]：在t0时刻，功率开关S1导通，二极管D1～D4关断，D5导通，等效电路如图4（a）所示。此时，电感电流线性上升，C1、C5、C6、CS放电，C2和C4充电，并且电容C7由C6充电。在模态1下，通过在图4（a）所示电路上应用基尔霍夫电压定律KVL（Kirchhoff voltage law），可以推导出以下关系：

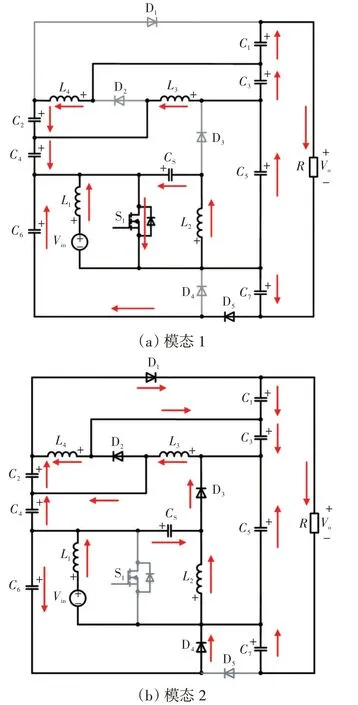
图4 各模态等效电路Fig.4 Equivalent circuit in each mode

式中：VL1～VL4分别为电感L1～L4的电压；VC2、VC3、VC4、VC5和VCS分别为电容C2、C3、C4、C5和CS的电压。

2）模态2

[t1～t2]：在t1时刻，功率开关S1断开，二极管D1～D4导通，D5关断，等效电路如图4（b）所示。此时，电感电流线性下降，C1、C5、C6、CS充电，而C2、C4、C7放电。在模态2 下，通过在图4（b）所示电路上应用KVL定律，可以推导出以下关系：

式中，VC1为电容C1的电压。

此外，根据图4 所示模态1 和2等效电路，可以通过KVL定律推导出以下关系：

式中，VC6和VC7分别为电容C6、C7的电压。

1.2.2 断续导通模式分析

当变换器工作在DCM 时，会存在3 种工作模态，其中前两个模态与CCM 下的工作模态1和2相同，DCM下第3个工作模态等效电路如图5所示，此时，功率开关S1维持关断，电感电流线性下降至模态3，此时电感L1电流不再发生变化，电感L2～L4电流反向流动，且大小不发生变化，电感两端的电压为零。因此二极管D4～D5电流为零，处于关断状态。C1、C2、C3、C4、C7处于放电状态，C5处于充电状态。变换器处于DCM下的主要波形如图3（b）所示。

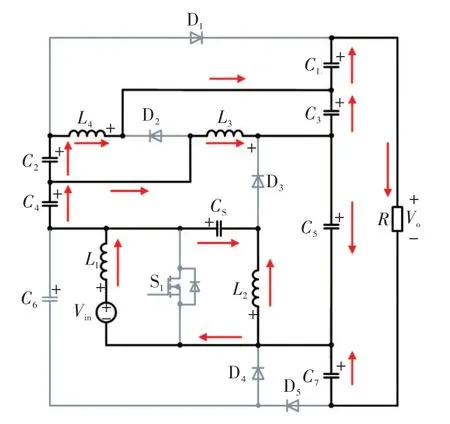
图5 DCM 下模态3 的等效电路Fig.5 Equivalent circuit in Mode 3 of DCM

1.3 电压增益分析

（1）CCM：通过在电感L1～L4上应用伏秒平衡规则，联立式（1）～（3）可得

由式（4）可以推导出所提变换器输入电压Vin和输出电压Vo的关系为

由此可得变换器的电压增益MCCM为

（2）DCM：由各模态等效电路图可得，电感L1～L4电流和二极管的平均电流(ID1-avg,ID2-avg,ID3-avg,ID4-avg)的总和有如下关系，因此

式中：iD1、iD2、iD3、iD4分别为二极管D1～D4的电流；IL1、IL2、IL3、IL4分别为电感L1～L4的平均电流；Io为输出电流，且Io=VoR。

由图4可得，定义二极管D1～D4平均电流之和为

式中：DZ为DCM下占空比；ID-peak为电感L1～L4的峰值电流之和，其计算公式为

式中：ILn-peak（n=1，2，3，4）为电感L1～L4电流峰值；Ln（n=1，2，3，4）为电感值。等效电感Leq的计算公式为

联立式（7）～（9）可计算出DCM下的占空比DZ为

式中：K为比例系数；R为负载电阻；fS为开关频率（fS=1TS）。由式（11）可得

通过图4 和图5 并对4 个电感应用伏秒平衡规则，可得到

求解式（13），可得DCM 下电压增益MDCM表达式为

当变换器工作在边界导通模式BCM（boundary conduction mode）时，此时MCCM=MDCM，可得到归一化的电感时间常数Kcritical为

当K>Kcritical时，变换器工作在CCM，反之则处于DCM。图6绘制了Kcritical与D的关系曲线。

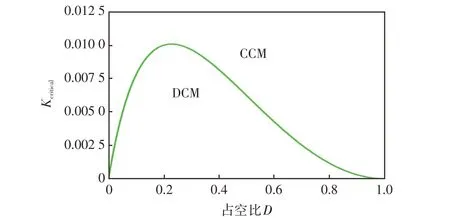
图6 所提变换器在CCM 和DCM 工作之间的边界条件Fig.6 Boundary condition between CCM and DCM operations for proposed converter

1.4 电压应力和电流应力分析

由图4所示CCM下各模态等效电路，可以推导出半导体器件的电压应力表达式为

式中：VS1为功率开关S1的电压；VD1、VD2、VD3、VD4和VD5分别为二极管D1～D5的电压。

根据式（6）和式（16），可以将上述半导体器件的电压应力用归一化形式表示为Vo和M的函数，即

假设变换器工作在无损耗状态，即VinIin=VoIo，Iin为输入电流。因此，电感电流IL1和IL2～IL4计算式分别为

与第1.3 节公式推导相似，通过在图4 所示CCM 下等效电路上应用基尔霍夫电流定律KCL（Kirchhoff current law），其功率开关和二极管上的电流应力可推导为

式中：iS1为功率开关S1的平均电流；iD5为二极管D5的电流。

1.5 非理想状态下的电压增益

在实际工作过程中，变换器中的各器件会存在寄生参数，从对变换器的电压增益产生影响。为了探究其考虑器件寄生参数时的电压增益，建立了变换器的非理想模型，如图7所示。

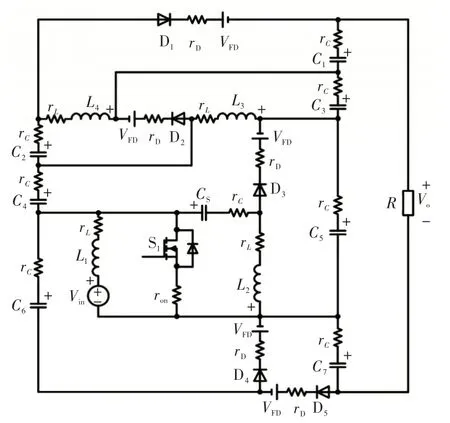
图7 带寄生参数的变换器拓扑结构Fig.7 Topology of converter with parasitic parameters

在变换器的非理想模型中，电感器等效串联电阻ESR 由电阻rL表示。功率开关的导通电阻由电阻ron表示。二极管导通电阻和正向电压分别由电阻rD和电压VFD表示。电容的ESR 由rC表示。在考虑了这些寄生参数后，所提出的变换器在其非理想模型中的电压增益M′为

式中，ki（i=1，2，3，4，5）为比例系数。

图8 绘制了所提变换器的理想和非理想状态的电压增益曲线对比，根据器件手册，选取元件寄生参数值如下：Vin=40 V，rL=35 mΩ，rC=200 mΩ，rD=80 mΩ ，ron=25 mΩ ，VFD=1.3 V ，R= 800 Ω。结果表明，当D在0～0.7区间时，M′≈10，变换器的非理想状态的电压增益接近理想状态的增益，这表明所提出的变换器具有高升压能力。

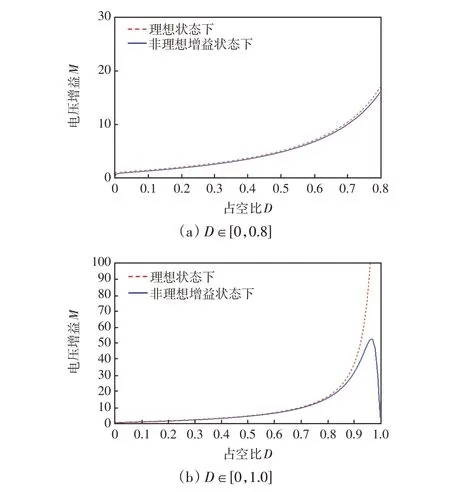
图8 理想状态与非理想状态电压增益曲线Fig.8 Voltage gain curves in ideal and non-ideal states

2 变换器性能对比

将所提变换器与其他非隔离升压变换器进行比较。表1总结了这些变换器的电压增益、半导体器件上的归一化电压应力（VSVo）和（VDVo）、器件数量和输入电流纹波大小。图9（a）显示了表1 中变换器的M与占空比D的关系，而图9（b）和（c）分别显示了表1 中变换器的开关管和二极管的最大归一化电压应力。

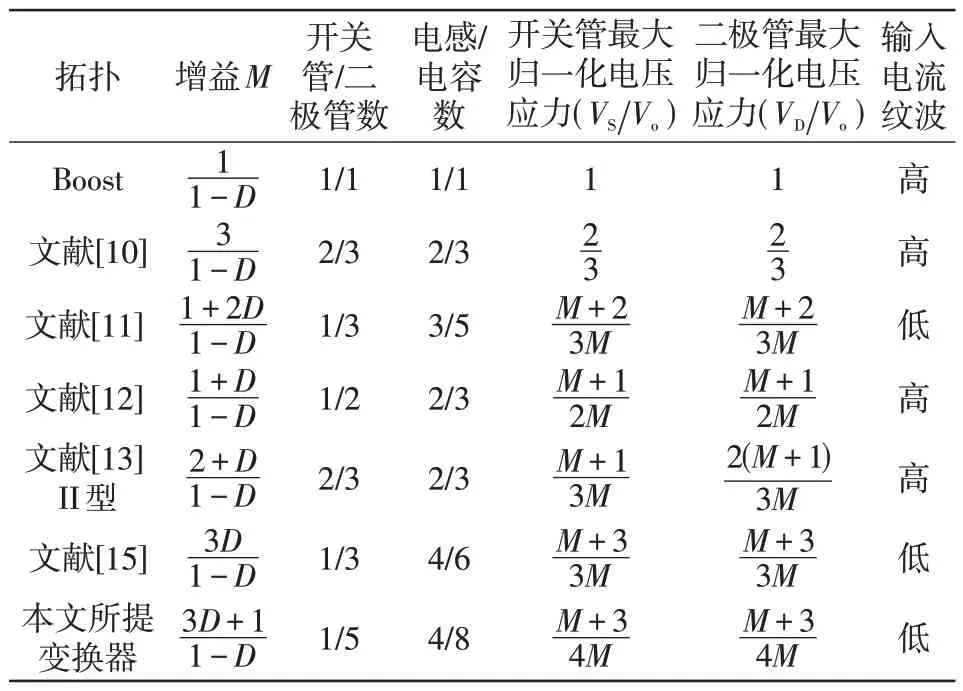
表1 变换器性能总结Tab.1 Summary of performance of different converters

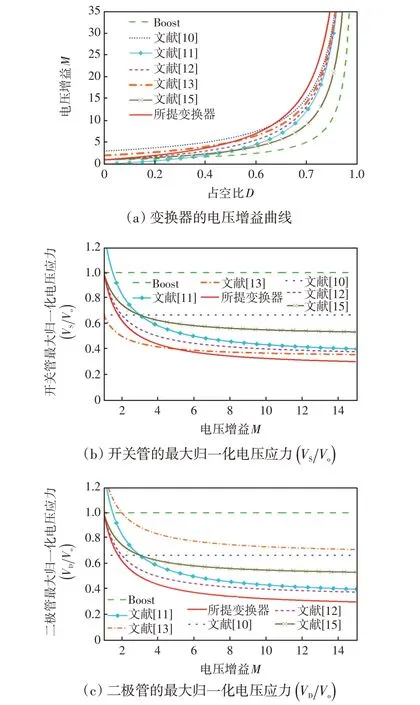
图9 变换器性能比较Fig.9 Comparison of performance among converters

从图9（a）可以看出，所提变换器电压增益范围更宽，且当D<0.5时，除文献[10，13]外，所提变换器电压增益明显高于另外4种变换器。但文献[10，13]引入了额外的功率开关，且输入电流纹波较大。当D>0.5时，所提变换器电压增益最高。

图9（b）表明，将半导体器件电压应力进行归一化处理后进行对比，当电压增益处于较高水平时，所提变换器功率开关电压应力明显小于Boost变换器及文献[10-13，15]中所提变换器的功率开关所受电压应力。图9（c）显示，在全增益范围内，与其他6种变换器相比，所提变换器的二极管电压应力最小，且始终处于较低的水平。从上述对比中可以明显看出，所提变换器集成了许多优点：高电压增益、宽电压增益范围、半导体器件上的低电压应力、低输入电流纹波，并且使用单个功率开关，这使其更适合应用在光伏发电并网系统中。

3 变换器衍生拓扑分析

3.1 衍生拓扑结构

由上述分析，可以根据所提变换器拓扑结构提取出一种外部升压电路，如图10所示。

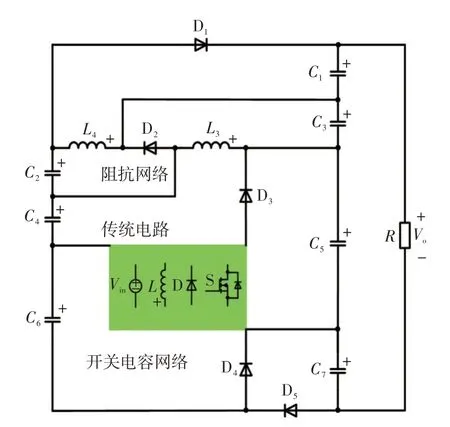
图10 所提变换器外部结构Fig.10 External structure of the proposed converter

阻抗网络与开关电容网络构成的外部升压结构，共同作用提升内部电路增益，此外由于输出电容采用多电容堆叠方式，降低了单个电容承受的电压应力。同时利用二极管和电容电压的箝位作用降低了半导体器件的电压应力。内层电路为传统单开关升压变换器，其输入源与电感直接连接，未在输入端分接其他升压结构，实现了较低的输入电流纹波。

表2 给出了以传统单开关升压变换器为内部电路而形成的一类新型升压DC-DC 变换器的衍生拓扑结构分别为Boost 变换器、准Z 源变换器、二次型变换器。同时列出了衍生拓扑的主要性能指标，经仿真验证和理论分析，该类变换器均具有升压能力强、半导体器件电压应力低的特点。同时，内部电路为单开关升压变换器，控制简单，且输入电流纹波较小。

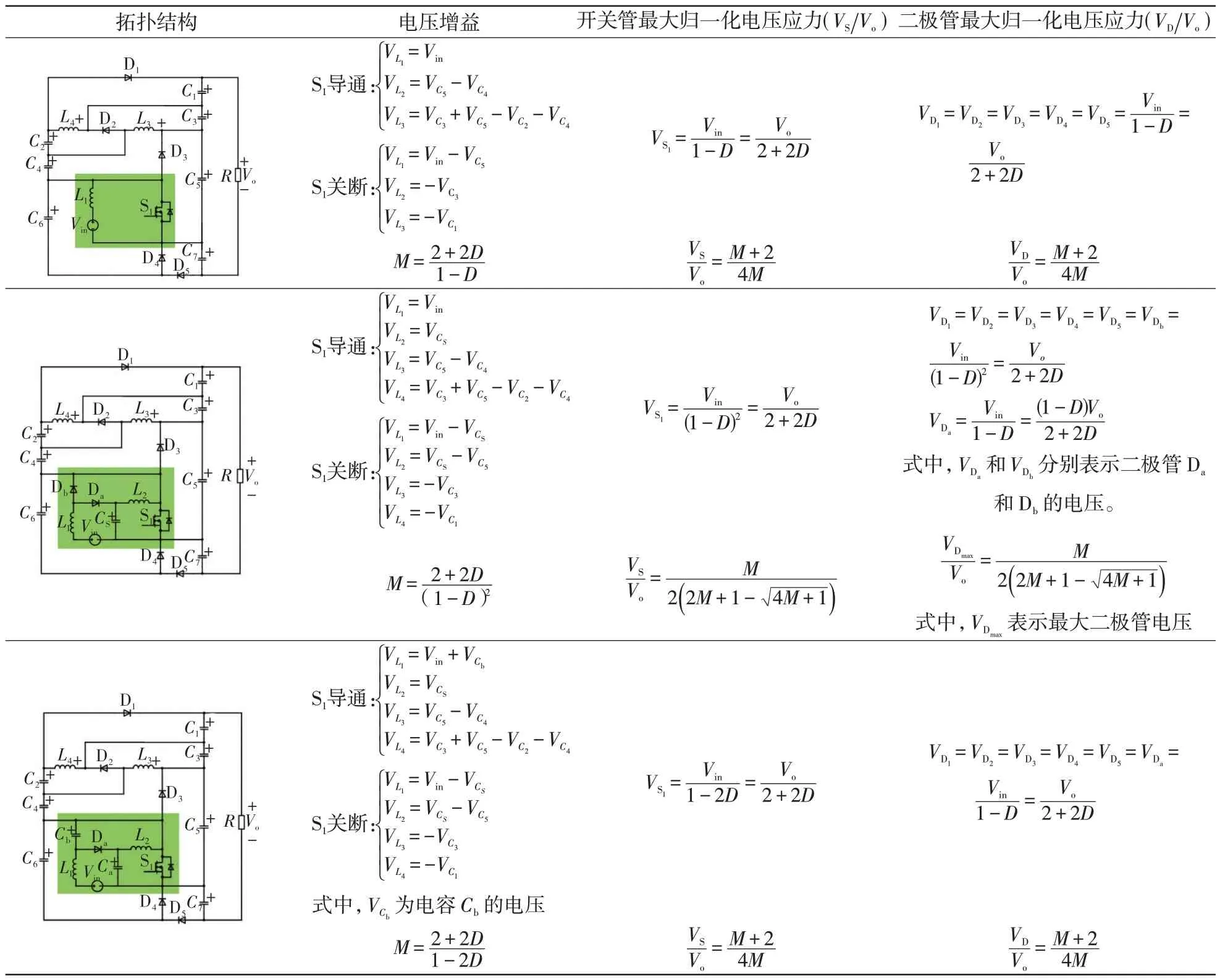
表2 衍生拓扑性能分析Tab.2 Performance analysis of derived topologies

3.2 仿真验证

为了验证上述分析的有效性，在PSIM 软件中搭建了所提3个变换器的仿真模型，并对结果进行了比较。所有变换器的输入电压和开关频率分别设置为40 V 和100 kHz。为了便于比较，调整输出电压为400 V，3个变换器各自的功率开关和二极管的电压应力仿真结果如图11所示。

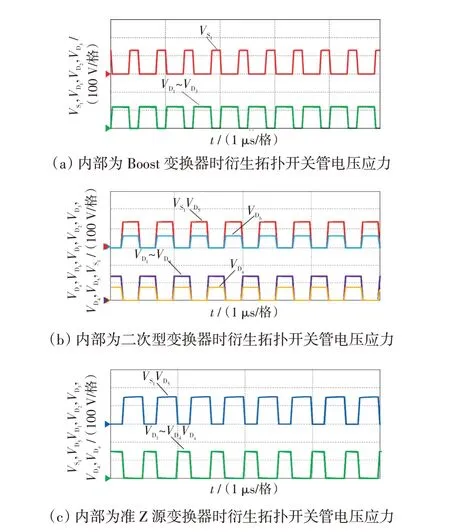
图11 衍生拓扑仿真结果对比Fig.11 Comparison of simulation result among derived topologies

4 元件关键参数设计

在开关管VS1导通时，通过式（18）可以计算出4个电感的电流。假设已知最大纹波电流为ΔiL1～ΔiL4，则有

由此可以得到所需的最小电感的表达式为

式中，ΔiLi（i=1，2，3，4，5）可以根据变换器在实际应用中的设计指标选取。

类似地，通过确定电容的最大纹波电压ΔVC1～ΔVC7及ΔVCS的大小，并由式（3）和（4）可得到所需的最小电容表达式为

式中，ΔVC通常取VC的5%[22]。通过确定变换器所需的最大电压增益和最大输出负载电流，可以根据式（17）计算出功率开关和二极管的最大电压应力，同时根据式（19）计算出流经功率开关和二极管的峰值电流。由半导体器件的最大电压应力和峰值电流来确定功率开关和二极管的具体型号。

5 实验验证

5.1 实验结果分析

为了验证所提出拓扑的可行性及其理论分析的正确性，搭建了1 个200 W/400 V 实验样机。样机设计指标为：输入电压Vin=40 V ，输出电压Vo=400 V，占空比D=0.7，开关频率fS=100 kHz。另外由式（22）和（23）可计算得：L1≥270 μH，L2、L3、L4≥500 μH；C1≥1.15 μF，C2、C6≥0.384 μF，C3≥0.77 μF，C4≥1.384 μF，C5≥1.15 μF，C7≥0.12 μF，CS≥0.865 μF。因此，电感L1取330 μH、L2、L3、L4均取510 μH，电容C1、C3、C5、C7取20 μF，C2、C4、C6、CS取5 μF。表3 中给出了样机的具体工作参数。实验测试结果如图12所示。

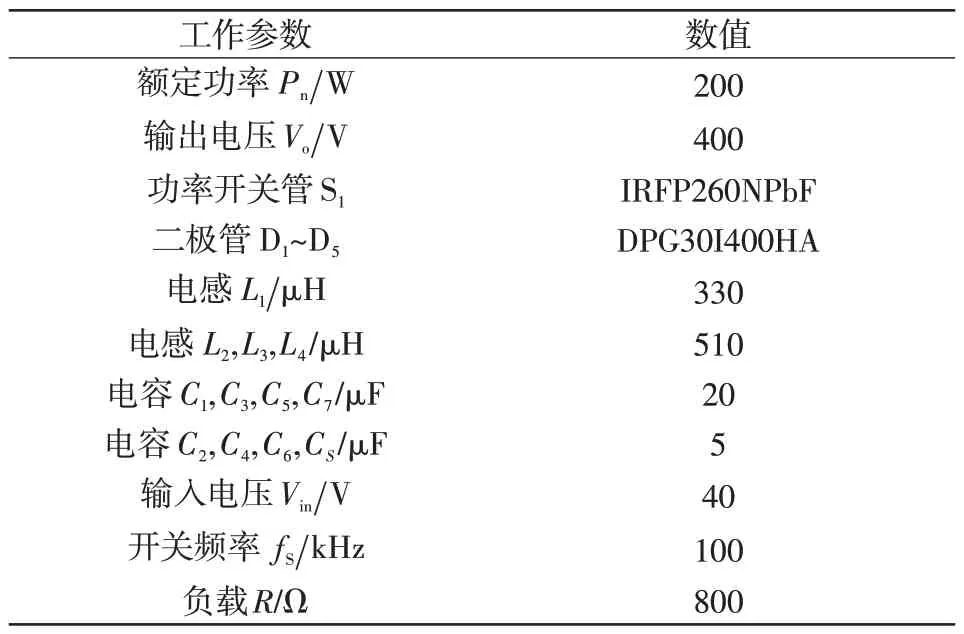
表3 样机工作参数Tab.3 Operating parameters of prototype

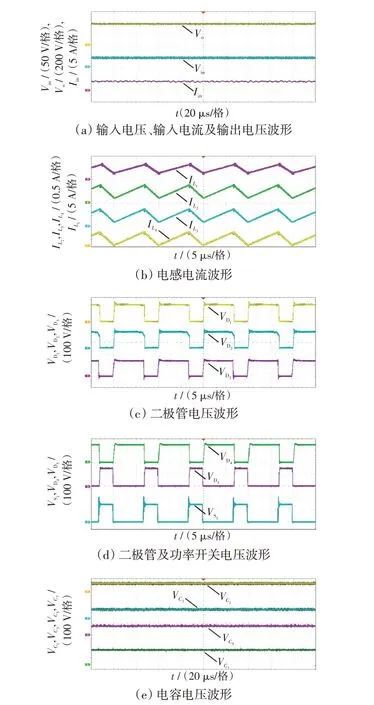
图12 实验结果Fig.12 Experimental results

输出电压Vo与输入电压Vin波形如图12（a）所示，其中Vo实测值为399.3 V，Vin为40.3 V。根据实验结果，实际电压增益为M≈9.9，此时样机效率为94.4%。结果表明该变换器具备高增益的特性。图12（b）为电感L1～L4的电流波形，实验结果显示，4个电感在1 个周期内同时充放电，且均连续，其中IL1的平均值为4.7 A，IL2=IL3=IL4≈0.45 A。这与式（18）的理论分析一致。图12（c）和（d）为功率开关和二极管的电压波形。半导体器件电压应力可以通过式（16）计算为133 V，这与图12（c）和（d）中所示的结果基本一致。图12（e）所示的输出端电容C1、C3、C5、C7的实测电压应力分别为VC1=89.9 V，VC3=90.1 V，VC5=90.0 V，VC7=129.3 V，与式（13）的理论分析一致。

5.2 效率和功率损耗分析

本节分析了所提拓扑结构的效率和功率损耗特性。首先基于考虑器件寄生参数的电路仿真和理论计算得到了功率损耗的详细分布。其次，结合理论计算和硬件实验绘制了样机的效率曲线，分析了影响效率的因素。

图13 为输出功率200 W 时所提变换器的各部分损耗分布。总损耗为10.812 W，其中，开关管损耗最大，占比为52.3%，其次是二极管损耗，占比26.6%，电感损耗占比19.2%。由图13 可以看出电容损耗占比最小，为1.9%。

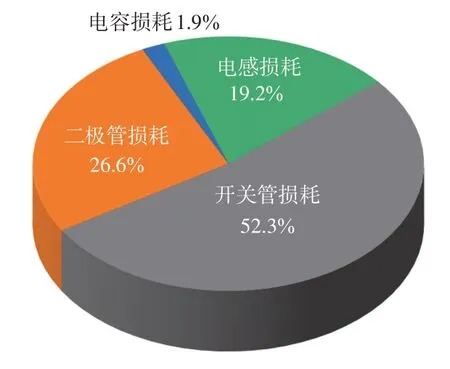
图13 所提变换器功率损耗分布Fig.13 Power loss distribution of the proposed converter

根据理论计算和硬件实验，绘制了样机工作在输入40 V，输出400 V，输出功率从60 W 升至200 W 的效率曲线，如图14（a）所示。可以看出，随着输出功率的增加，变换器效率呈现先增加后下降的趋势，其最大效率为94.75%，满载效率为93.80%。图14（b）绘制了样机工作在200 W，输出电压维持在400 V的情况下，输入电压从40 V增加到100 V 时，效率随输入电压变化的曲线。从图中可以看出，效率随输入电压增大而增大，即增益越高效率越低。输入为40 V 时效率最低为93.80%；输入电压为100 V 时效率最高为96.54%。当输入电压较高时，变换器工作在较低的占空比下，导通损耗相应有所下降，因此效率增加。

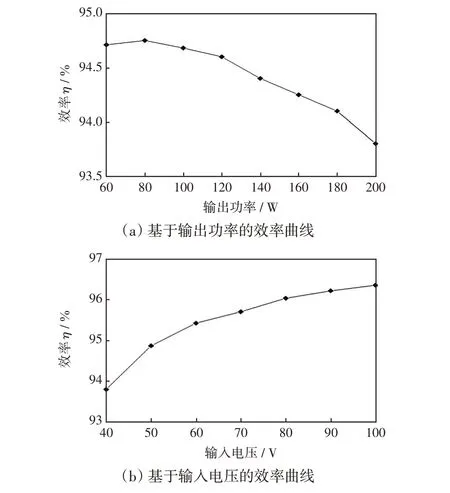
图14 所提变换器效率曲线Fig.14 Efficiency curves of the proposed converter

图15 为所提变换器与文献[15-16]效率对比。由图可知，相较于文献[15-16]所提的2 种改进型SEPIC 变换器相比，本文所提变换器具有更高的效率。因为对于相同的电压增益，文献[15]中的变换器需要在更高的占空比下工作，因此增加了导通损耗。而文献[16]由于采用了2 个开关管，其开关管损耗有所增大，进而影响了效率。

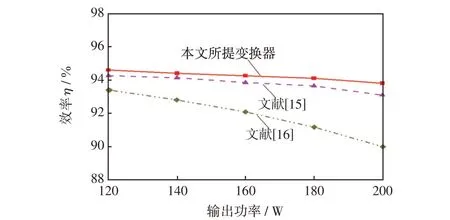
图15 所提变换器与文献[15-16]效率曲线对比Fig.15 Comparison of efficiency curve between the proposed converter and those in Refs[15-16]

6 结 论

经过对现有高增益变换器电压增益低、半导体器件应力较高等问题的分析，文中提出了一种基于SEPIC的高升压DC-DC变换器，并对其稳态特性和原理进行了研究。在此基础上，进一步探究了基于所提变换器外部升压网络的衍生拓扑结构及其主要性能指标。最终，通过1 台400 V/200 W 的实验样机对所提变换器进行了可行性验证。研究表明，所提拓扑结构具有如下特点：

（1）其外部阻抗网络和开关电容网络的组合可以有效提升内部变换器电压增益至（2+2D）倍；

（2）整体半导体器件的电压应力远低于输出电压值的一半，有利于降低器件损耗和提升效率；

（3）仅使用单个开关，控制简单方便，易于设计驱动电路；

（4）基于可嵌套的外部升压结构，可根据实际应用需求进行内部变换器的选择，具有很高的灵活性和实用价值；

（5）所提变换器在器件数量上增加，对变换器整体效率和成本有一定影响，由功率损耗分析，电容损耗占比较小，因此电容数量增加未对变换器效率造成明显影响。

本文所提变换器开关器件电压应力较低，可以选用低导通电阻和更快开关速度的开关器件，在一定程度上可以减少损耗。除此以外，由于较低的电压应力，在变换器设计过程中可以选择低耐压、低成本的器件。综上所述，本文所提变换器具有较好的应用前景。