基于VMD 和改进聚类算法的配电网故障选线方法

王远川，李泽文，夏翊翔，毛紫玲，郭欣玉

（长沙理工大学电气与信息工程学院，长沙 410114）

目前我国中低压配电网普遍采用小电流接地方式，大数据统计显示，一年中单相接地故障发生的次数达到配电网所有发生故障的80%左右[1]，故障可能会引起系统局部电压过高，进而对电气设备造成破坏[2]，严重时甚至会危及人员的生命安全，因此需及时找出故障线路并予以切除。

基于主动注入法[3-5]和被动检测法的故障选线方法是目前常用的两种方法。通常，主动注入法易受过渡电阻的影响，且成本相对较高，适用性不强；被动检测法可分为基于稳态信息[6-7]和基于暂态信息的故障选线法[8-10]。实际运行中，诸多因素都会对传统的基于稳态信息的故障分析法造成干扰[11]，使得该方法很不可靠[12]。相比之下，基于暂态信息的故障分析法，凭借自身诸多优点[13-14]，被广泛应用于电力系统故障选线、行波定位等电网保护领域。许多故障特性，例如信号的相位、幅值、极性变化等，都存在于高频暂态信号中[15-17]，如果能被有效地分解、提取出来，就能够为选线提供思路。例如，文献[18]采用小波分解将故障零序电流分解后，通过比较各线路在特征频带中的幅值和极性来鉴别故障线路。但在特定分解尺度下，小波变换不能同时在时间和频率上都具有很高的精度，以及小波变换是非自适应性的，基函数选定了之后就不能在分解过程中改变，其选择可能会对分解结果产生影响。针对这些问题，经验模态分解EMD（empirical mode decomposition）算法被运用在故障选线领域，其能依据数据自身的时间尺度特征来将信号分解为若干模态分量，如文献[19]使用EMD算法对各线路导纳进行分解，提取出特征分量，通过比较故障线路和非故障线路的特征分量符号进行选线。但是EMD 分解存在端点效应和频率混叠等问题。此后，又相继诞生了集合经验模态分解EEMD（ensemble empirical mode decomposition）和互补集合经验模态分解CEEMD（complementary ensemble empirical mode decomposition）等改进型算法，但始终存在分解效果不理想的问题。

有一类利用形态学选线的方法，其对分解后的零序电流采用相关性聚类算法来鉴别故障线路，如文献[20]使用凝聚层次聚类HAC（hierarchical agglomerative clustering）算法来计算不同线路零序电流相似性测度并聚类，但HAC 算法时间复杂度高，且具有贪心算法的缺点。又如，文献[21]使用的基于划分算法的K-means 聚类算法具有步骤简单、时间复杂度、空间复杂度低的优点，但该算法易受初始聚类中心选取的影响[22]，且运算效率不及在其基础之上改进的一系列算法。

针对上述情况，为了高效、准确地选出故障线路，本文提出了一种基于变分模态分解VMD 和Kmeans++聚类算法的故障选线方法。首先对提取到的零序电流信号进行VMD 分解，得到有限个自适应频带特征的本征模态函数IMF（intrinsic mode function）；而后通过对其中的低频分量作相关性计算，对高频分量测算其初始极性，从而确定代表各出线零序电流信号的散点在二维平面内的横、纵坐标；最后通过K-means++聚类算法检测点集的分布情况，将故障线路筛选出来。

1 故障零序电流的分析计算

1.1 小电流接地系统解析

配电网发生单相接地故障示意如图1 所示。图1 中，rp、Lp分别为消弧线圈的等效电阻和等效电感值；Rf为接地过渡电阻；C0j为第j条线路Lj的对地电容大小；i0j为线路Lj上流过的零序电流；iL为消弧线圈上流过的感性电流；U0f为零序电压源。

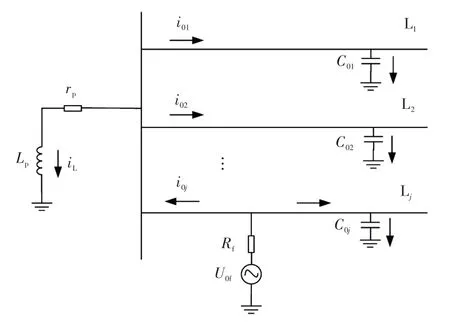
图1 零序电流分布Fig.1 Zero-sequence current distribution

由图1 可知，发生单相接地故障后，系统中各条健全线路首端流过其本身产生的容性电流，这些电流都将经过接地点流入故障线路中。因此，零序电流在故障和健全线路中的流向刚好相反，在非故障线路中为出线端向线路末端，而在故障线路中则为线路末端向出线端，这也导致故障线路中的容性电流与健全线路中的容性电流初始极性理论上也是相反的。值得注意的是，消弧线圈中此时将产生一个与接地点处容性电流相位相反的感性电流，该电流经电感线圈注入大地再经接地故障点流入故障线路中。

1.2 故障零序电流的分析

建立单相接地故障时的暂态分析等值电路模型，该电路如图2所示。

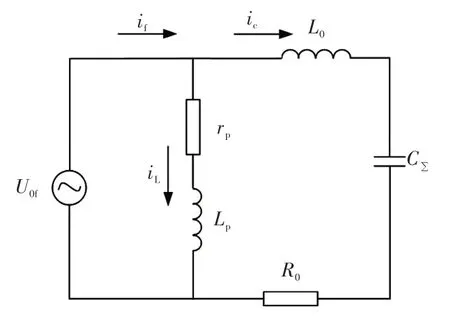
图2 系统暂态分析等值电路Fig.2 Equivalent circuit of transient analysis of system

图2 中，R0、L0分别为配电网的等值电阻、电感；C∑为系统零序电容之和；if为总故障电流；ic为暂态电容电流。

根据基尔霍夫电压定理列写图2 中等效电路回路的微分方程为

式中：φ为故障时刻电压初始相角；Um为系统相对地的电压幅值；ω为工频角频率；t为时间。

对上述微分方程求解，可得故障点处流过的容性电流和感性电流的计算公式为

式中：、分别为容性电流的高频振荡与工频交流分量；为感性电流的工频交流分量；iLdc为感性电流的衰减直流分量；Icm、ILm分别为容性电流、感性电流的幅值大小；ωf为暂态自由振荡分量的角频率；β为自由振荡分量的衰减系数；τL为回路的时间常数。

容性电流和感性电流相加可得故障点处流过的总电流if，即

由于衰减直流分量只存在于感性电流中，因此其只会随着感性电流从接地故障点流入故障线路。根据接地故障点电流表达式可以看出，故障零序电流的特征不仅与配电线路本身一系列固有参数相关，其各组成部分的幅值也会随着故障初相角取值大小的改变而变化。根据容性电流高频振荡分量的表达式可知，其波形振幅很大程度上取决于sinφ的大小；而对于感性电流中的衰减直流分量，其波形振幅大小取决于cosφ的大小。因此当故障电流直流分量数值较大时，高频振荡分量一般较小；反之，当高频振荡分量数值较大时，衰减直流分量一般较小。

例如，当φ=0°时，故障电流表达式可化简为

从式（6）可以看出，接地故障点处零序电流含有全部的3 个分量，且衰减直流分量幅值较大，而高频分量幅值较小。

当φ=90°时，故障电流表达式可化简为

从式（7）可以看出，此时故障零序电流主要由高频分量与工频分量所组成，且高频分量有着较大的幅值，而几乎不含有直流分量。

2 变分模态分解基本原理

VMD算法具有自适应和完全非递归性[23]，其将信号的分解问题转化为构建变分问题并求解，寻找变分问题的最优解，保证分解后得到的序列为具有中心频率和有限带宽的模态分量，实现各频率下本征模态函数IMF（intrinsic mode function）的有效分离，得到预设分级层数下的K个模态分量。其核心步骤由变分约束问题的构造和求解构成。

首先，构造变分约束问题，其数学表达式为

式中：f为待分解的原始信号；∂t为梯度运算；δ(t)为单位脉冲；j为虚数单位；{uk} ={u1,u2,…,uK} 为分解后得到的K个本征模态函数；{ωk} ={ω1,ω2,…,ωK} 为各模态分量的中心频率。通过引入惩罚因子α和拉格朗日算子λ，构造增广拉格朗日表达式，即

通过使用交替乘法算子迭代、计算式（9），得到其鞍点即为变分约束问题的最优解。各个模态分量和其中心频率的迭代公式为

如果满足，则将目前得到的各IMF作为输出量输出；若不满足，则回到式（10）和（11）继续进行迭代更新。

3 选线相关算法原理及判据构造

结合第1.2节对发生单相接地故障时故障零序电流组成及其相关特征的解析可知，含有衰减直流分量的感性电流只流入故障线路中，这将使故障发生初期故障线路零序电流低频分量的幅值远大于健全线路，从而产生波形上的差异；又由于零序电流在故障和健全线路上的流向相反，故障线路与健全线路零序电流信号高频分量的初始极性也应当是相反的，因此无论是低频分量还是高频暂态分量，故障线路相比于非故障线路均存在着明显的差异，如果能将这种差异投射到二维平面或者三维空间中，将有利于筛选出故障线路。

第1.2 节提到，故障电流衰减直流分量数值较大时，高频振荡分量往往较小；反之当高频振荡分量较大时，衰减直流分量往往较小。换言之，一方差异较为明显时，另一方差异有可能难以辨识。因此，本文选择综合考虑二者的差异，将其投射到二维平面中，通过对电流信号低频分量相关系数与高频分量初始极性差异构造的二维平面点集进行聚类，从而准确选出故障线路。

3.1 VMD 分解相关参数取值的确定

对采样信号做VMD 分解之前，需要提前设定好分解层数K、惩罚因子α以及预设精度ε[24-25]。

故障零序电流信号经过VMD 分解后将得到K个子模态分量，每个子模态都有各自的中心频率。VMD算法与EMD等其他分解方法的一个很大的不同点在于，其需要人为预先设定K的取值。

零序电流信号中的高频振荡分量的振荡频率浮动区间大致为1 000～3 000 Hz，与工频分量和直流分量相差巨大；而工频分量与直流分量之间频率相差不大。考虑到实际采集的信号往往含有噪声，因此本文所有的仿真信号都将注入25 dB的噪声作为干扰。

本文最终采取的分解方式为：先使用FIR 滤波器滤去频率过高的噪声信号（在仿真实验时取5 500 Hz 作为滤波界线），而后截取故障发生时刻后2 个信号周期（40 ms）的零序电流信号先做2 层分解，得到的模态分量分别记为IMF1和IMF2。高频振荡分量与过滤后剩下的噪声信号将全部分解到IMF2中，而衰减直流、工频交流分量和低次谐波则全部存在于IMF1中。将得到的IMF1分量再次做2层分解，得到的模态分量分别记为IMF1-1与IMF1-2，这样衰减直流分量和工频分量被全部分解到IMF1-1中，低次谐波分量则被分解到了IMF1-2中。由此各模态分量根据频率由低到高（IMF1-1、IMF1-2、IMF2）的主要成分如表1所示。

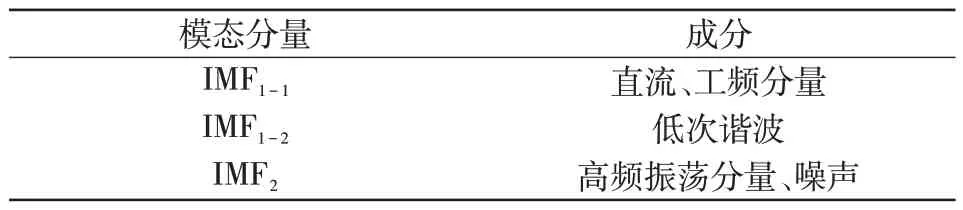
表1 各模态分量的主要成分Tab.1 Main components of each modal component

惩罚因子α的取值会对模态分量的带宽产生影响，研究表明α值的大小与模态分量的带宽成反比例关系。α的值越小，信号带宽越大，各模态分量的函数会有很大一部分频率重叠部分，即模态混叠；α的值越大，信号带宽越窄，模态分量向中心频率收敛速度越快，故障波形中的重要信息存在丢失的可能性。根据以往的VMD分解经验，α的取值范围通常在2 000～4 000。本文经过多次实验，结合电网实际运行中的工况，选择α的取值为4 000，预设精度ε的值取为1×10-6。图3 是某条件下的故障线路信号波形，其分解结果如图4所示。

图3 某条件下的故障线路信号波形Fig.3 Fault line signal waveform under certain conditions

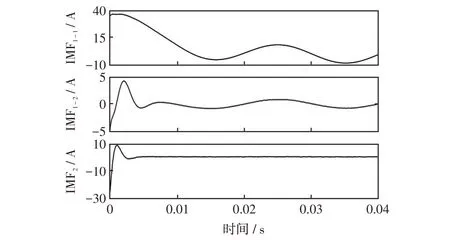
图4 信号分解结果Fig.4 Signal decomposition results

3.2 二维平面散点图的构造

选择采用数学形态学中皮尔逊相关系数来反映不同出线上零序电流低频分量IMF1-1的相关性，其公式为

式中：ai、bi分别为a、b两个信号的第i个采样点的值；n为采样点个数；ρ表示两者的相关性，-1≤ρ≤1。ρ越趋近于-1，两波形之间相关性越低；ρ越趋近1，两波形之间的相关性越高。假设配电网共有m回出线，对各出线首个信号周期（20 ms）内的IMF1-1分量进行相关性计算，得到它们之间的相关系数{ρij} ={ρ11,ρ12,…,ρmm} ，ρij表示出线Li与Lj低频信号分量IMF1-1之间的相关系数。将每一个出线看作二维平面的一个散点，各散点横坐标为该点所代表的出线IMF1-1分量与其他出线（包括其自身）的IMF1-1分量相关系数之和。例如，代表线路Li的点的横坐标xi表达式为

各散点纵坐标构造方法如下。首先对各线路IMF2分量做一阶差分计算，即

式中：diff为一阶差分计算符号；IMFi-2表示出线Li的高频分量；n为采样点个数，当n=1时，式（15）为信号的一阶差分初值。

然后使用符号函数计算其一阶差分初值的极性，确定各线路高频分量的极性，以表示其纵坐标。例如，代表线路Li的点的纵坐标yi表达式为

式中，sgn为符号函数，当信号初始极性为正时，sgn的值为1；当信号极性为负时，其值为-1。

故障特征较为明显时，故障线路零序电流低频IMF1-1分量波形与健全线路存在明显差异，因此它们之间的相关系数也将较小，而健全线路之间的波形差异则相对较小，相关系数较大并趋近于1。根据式（14），做相加运算后，故障线路的散点横坐标值会较小，而健全线路的散点横坐标值则较大，且数值比较接近；又由于高频IMF2分量初始极性存在差异，故障线路与健全线路散点的纵坐标值将为相反数。即使某一频段下故障特征不明显导致单一坐标无法区分故障线路，在二维平面中代表故障线路的散点依然是一个离群点。

3.3 K-means++聚类算法

基于划分聚类的K-means++算法的原理简单来说就是对一堆散点进行聚类，首先确定将这些散点聚成几类，然后挑选几个点作为初始中心点，并根据一定规则迭代重置聚类中心点，直到达到类中的点都足够近、类间的点都足够远的目标效果。传统的K-means 聚类算法采取随机选取的方式确定初始聚类中心，但最终的聚类结果可能会受到不同初始聚类中心选取的影响，从而对选线结果产生影响。K-means++的改进之处在于，其在选取初始聚类中心时可以确保初始聚类中心之间的距离尽可能地远，从而更高效、准确地进行聚类分析。

在本文中故障线路和非故障线路各自的散点分别形成一个簇（记为故障线路簇和健康线路簇），因此需要将所有散点划分为2类。由于故障线路所属的散点理论上属于离群点，K-means++聚类算法在首轮分类时即可将代表故障线路的散点单独划分出来，从而大大提高了运算速度和选线准确率。

该算法通过对各出线零序电流信号IMF1-1分量相关系数和IMF2分量初始极性差异构造的点集P={P1,P2,…,Pm} 进行聚类时的具体步骤为如下。

步骤1从输入的数据点集P中随机选一个点作为故障线路簇Q1和健康线路簇Q2的首个初始聚类中心c1。

步骤2分别计算点集中其他的点到该聚类中心的欧氏距离，根据距离尽可能远地原则选择一个点作为另一个初始聚类中心c2。用xci、yci表示聚类中心ci的横、纵坐标，第i个点到其的欧氏距离dis表示为

步骤3根据点集中所有点与这两个聚类中心的距离最短原则将它们划分到相应的线路簇。

步骤4重新计算两个簇各自的聚类中心，即

式中：z表示单个样本向量；|Qi|表示簇的大小。

步骤5将点集P中全部点根据与聚类中心欧氏距离最小原则进行划分。

步骤6计算标准测度函数，当满足收敛条件时，函数停止迭代，算法终止；如不满足则重复步骤3～步骤5。

3.4 选线流程

选线流程如图5所示，具体步骤如下。

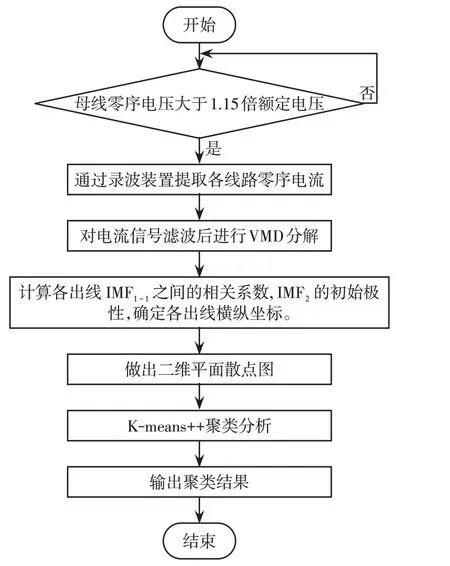
图5 故障选线流程Fig.5 Flaw chart of fault line selection

步骤1利用检测装置持续监测系统母线零序电压U0是否超过额定电压UN的115%，符合条件即启动故障选线装置，提取各出线在故障发生时刻后2个信号周期（40 ms）内的零序电流信号波形。

步骤2将提取到的各出线上的零序电流信号用VMD 算法按照前文所述方法先过滤后再进行3层分解，得到预设个数的本征模态函数。

步骤3根据式（13）和（16），通过对故障发生时刻后首个信号周期（20 ms）内的低频分量做相关性计算，对高频分量测算初始极性，进而确定各点横、纵坐标，作出二维平面散点分布图。

步骤4使用K-means++算法进行聚类分析，筛选出故障线路。

4 仿真分析

4.1 仿真模型

本节将在仿真的基础上分析验证本文所提算法的实用性。通过仿真软件Pscad 建立配电网模型，获得各出线单相接地条件下的零序电流信号波形；将零序电流信号导入Matlab工作区中进行VMD算法分解，获得故障信号不同频段下的模态分量；使用本文所提出的方法进行模拟选线，得到最终结果数据。

在Pscad中搭建一个6条出线6个负荷的10 kV配电网模型，其结构如图6所示。系统中，线路L1、L3、L4、L6为架空线路，除L1长度为15 km之外，其余长度均为12 km；线路L2为电缆线路，长度8 km；线路L5为缆线混合线路，电缆长4 km，架空线长12 km。各出线相关参数如表2所示，各负荷功率均设为2 MW，消弧线圈电感值采用过补偿10%进行设置。

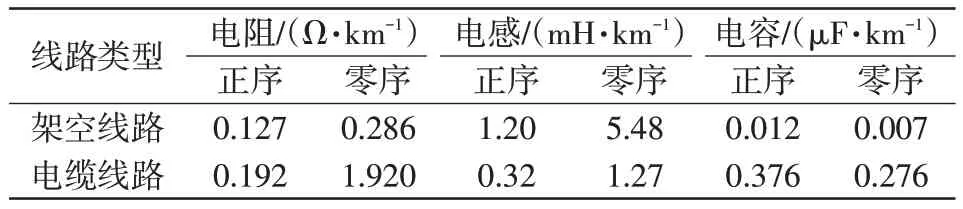
表2 线路参数Tab.2 Parameters of lines

图6 仿真电路模型Fig.6 Simulation circuit model

4.2 不同初始条件下的仿真

仿真实验选定的3 个变量分别是故障距离、故障初相角和接地过渡电阻。首先选取一个典型案例进行详细分析，随后在选定两个变量而不断对剩余的单一变量做出改变的情况下进行仿真实验，以验证本文所提出选线方法的适用性。

4.2.1 典型案例分析

假设距离出线L2始端4 km处发生A相单相接地短路故障，故障时刻为0.04 s，故障初相角设置为90°，接地过渡电阻大小设置为2 kΩ，通过故障录波装置提取出各出线上故障发生时刻后2 个信号周期（40 ms）的零序电流波形如图7所示。

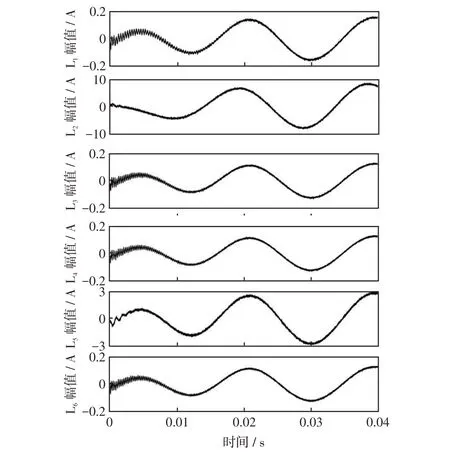
图7 零序电流波形Fig.7 Zero-sequence current waveforms

将提取到的电流进行滤波处理后，按照前文所述方式进行3层VMD分解，提取故障条件下各出线零序电流分解结果中的IMF1-1分量和IMF2分量分别如图8和图9所示。

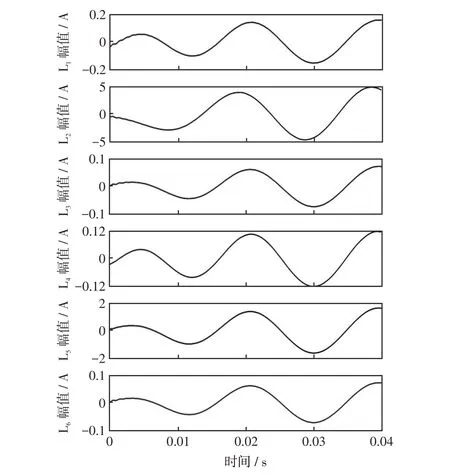
图8 各出线IMF1-1波形Fig.8 IMF1-1 waveform of each line

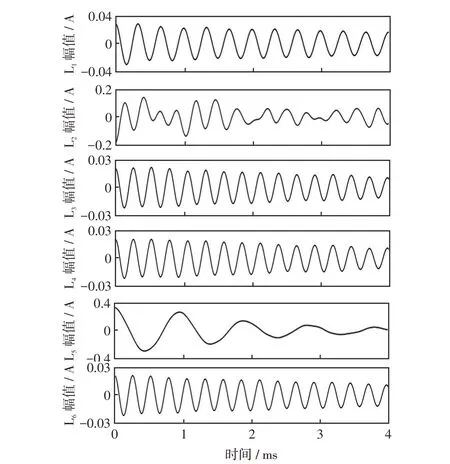
图9 各线路IMF2波形Fig.9 IMF2 waveform of each line

观察图8和图9中各出线上零序电流分解后得到的低频分量IMF1-1和高频分量IMF2可知，在故障初相角为90°的情况下，故障线路与非故障线路低频分量之间的波形差异不大，说明故障线路L2上流过的零序电流低频分量中几乎不含衰减直流分量；除故障线路L2的高频分量初始极性为正外，其余各线路中零序电流高频分量的初始极性全部为负。

算例的分解结果与本文第1 节中关于零序电流的成分及特性分析相吻合。

计算各出线IMF1-1分量之间的相关系数，所得结果如表3所示。

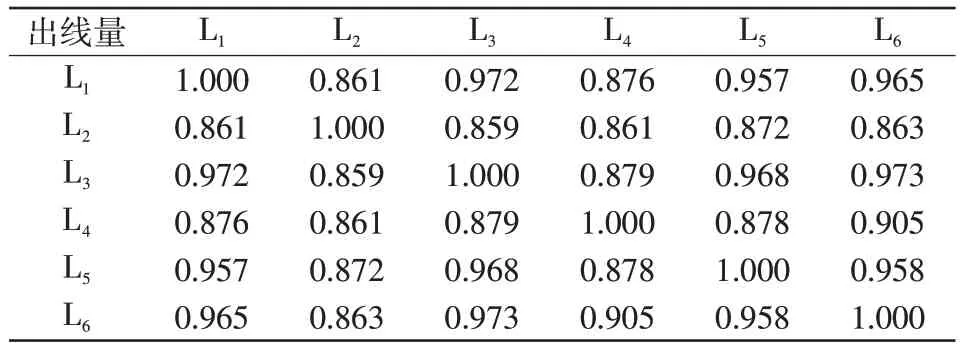
表3 各线路IMF1-1之间的相关系数Tab.3 Correlation coefficient between IMF1-1 of each line

计算各出线IMF2分量的初始极性，所得结果如表4所示。

表4 各线路IMF2的初始极性Tab.4 Initial polarity of IMF2 of each line

计算代表各出线的散点的横、纵坐标，并做出所有散点在二维平面分布，结果如图10所示。

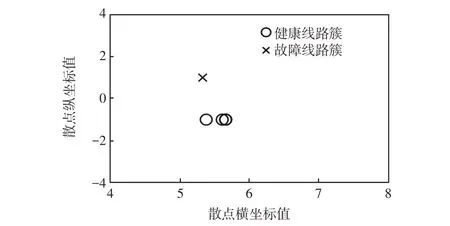
图10 二维平面的散点分布Fig.10 Scatter distribution on two-dimensional plane

从图中可以看到各散点的横坐标值均较为接近，代表仅通过低频分量之间的波形相关性并不足以使故障线路的散点成为离群点，必须通过纵坐标代表的高频分量初始极性之间的差异构造离群点。由于初相角φ=90°，高频分量初始极性差异较为明显，保证了故障线路与健全线路散点的纵坐标值为相反数，因此故障线路L2的点在平面中仍然成为了一个离群点。

使用K-means++聚类算法对图10 中的点集进行聚类分析，得到输出聚类标签为[2 1 2 2 2 2]，表示出线L2与其他线路不同，单独划分为了一类，因此可以得出结论为出线L2发生了单相接地故障。

4.2.2 适用性分析

选取故障初相角、故障距离以及过渡电阻为3个变量，在选定两个变量而不断对剩余的单一变量做出改变的情况下进行仿真实验。受限于篇幅不再详细分析，仿真结果如表5所示。

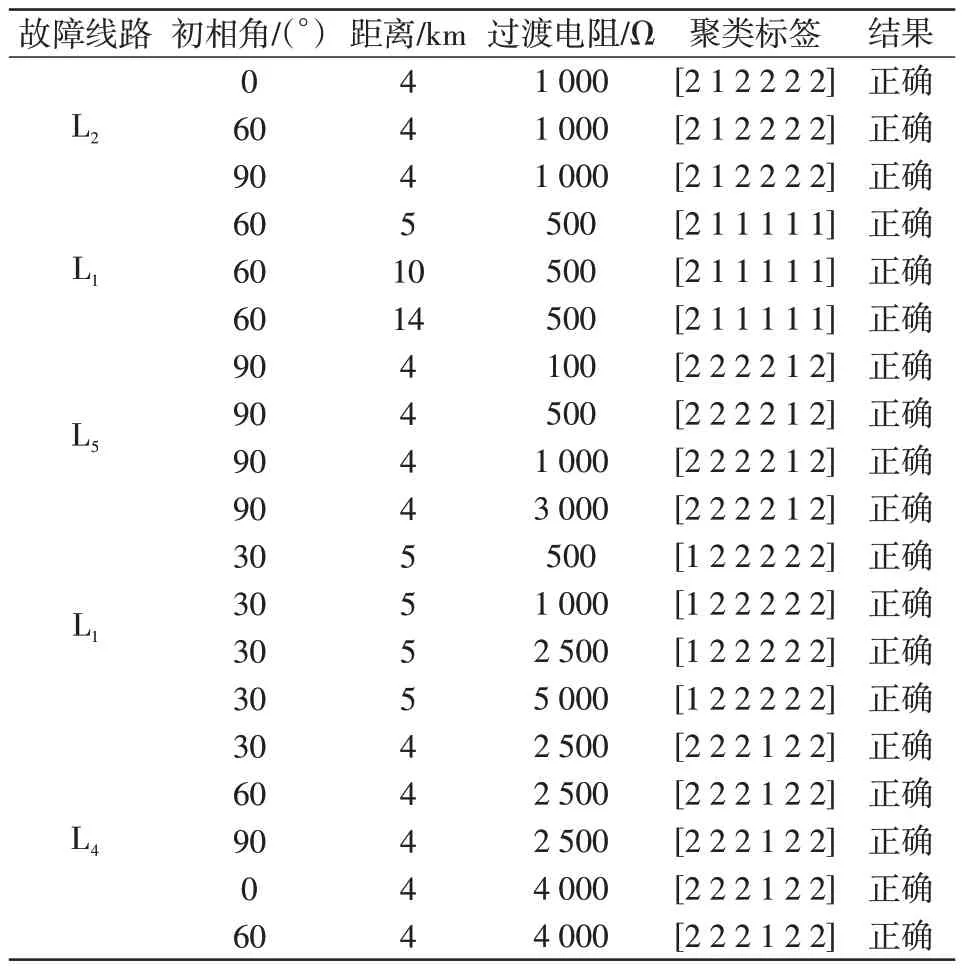
表5 仿真结果Tab.5 Results of simulation

从表5 中可以看出，不论故障初始条件如何改变，包括过渡电阻超过2 kΩ 等对选线不利的工况下，本文提出的算法依然能够准确地选择出故障线路。除表5中列举的情况，还进行了大量的仿真实验，包括改变噪声强度等，本文提出的算法均能正确地选出故障线路，表明该选线方法不受条件改变的影响，具有较强的适用性。

4.2.3 方法优越性比较

为验证本文所提出的方法的优越性，现假设在距离出线L5始端4 km 处发生单相接地故障，故障初相角设为60°，过渡电阻依次设置为100 Ω、500 Ω、1 000 Ω。分别用本文的方法和进行EMD分解再使用K-means++聚类（方法2）以及进行VMD分解再使用K-means聚类（方法3）进行比较，结果如表6所示。

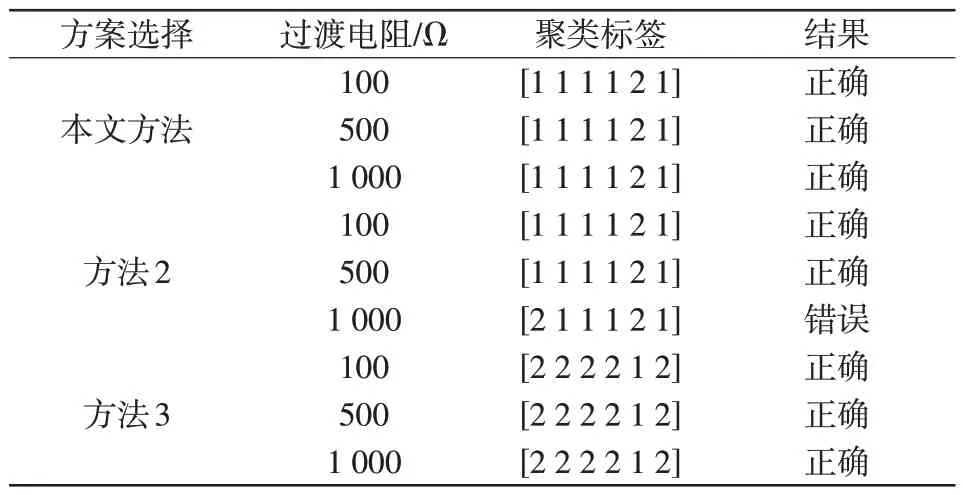
表6 不同方案的选线结果Tab.6 Line selection results under different schemes

通过对比3 种方法的结果可以看出，随着过渡电阻的增大，高频分量幅值的减小，本文的算法均正确地选择出了故障线路，而方法2 有错误记录。方法3 虽然也能正确选线，但是相较本文算法，Kmeans 算法在执行聚类任务时运行更加耗时（约为40 ms），约为K-means++算法（约为10 ms）的4 倍，因此本文设计的选线方法优于基于EMD分解或Kmeans聚类的相关性分析方法。

5 结 论

通过对谐振接地系统单相接地短路故障时故障零序电流组成特性的分析，本文提出了一种基于VMD 分解和改进K-means++相关性聚类的故障选线方法，实现了精确故障选线的目的。主要结论如下。

（1）本文将VMD分解和K-means++聚类算法相结合，利用在构造的散点图中，故障线路信号所属的散点属于离群点的特点，使用由K-means 聚类算法改进而来的K-means++聚类算法进行分析，相比于K-means算法，提高了选线速率。

（2）本文将故障零序电流信号不同模态分量之间的差异投射到二维平面中，从两个维度进行聚类分析，极大提高了选线准确率和保护裕度。

（3）加入噪声进行仿真实验，结果表明本文方法对噪声具有一定的鲁棒性。