双泵分腔调控电液负载模拟系统复合滑模控制

张俊琪，汪成文，2，赵二辉

(1.太原理工大学机械与运载工程学院，山西太原 030024；2.太原理工大学新型传感器与智能控制教育部重点实验室，山西太原 030024)

0 前言

电液负载模拟器是一款半实物仿真装置，它能够模拟舵机在现场条件中所承受的载荷，从而能检测舵机中的机械系统和控制系统的性能，为舵机的运行提供科学的参考根据，它主要起节约成本、降低实物实验中风险以及缩短研发周期的作用[1-3]。但只有实现高精度加载，电液负载模拟器才能具有以上作用，这样的半实物仿真装置数据才是有意义的。然而，电液负载模拟器的加载精度主要受舵机运动以及加载作动器摩擦力等干扰所影响。为提升电液负载模拟器的加载精度，国内外学者进行了深入的研究。

李阁强等[4]提出了一种新的加载执行元件设计方案，采用复式双层结构，其中外层结构用于跟踪舵机，从根本上解决了舵机运动的干扰问题。刘晓琳等[5]设计了一种复合式缓冲液压缸结构，能够缓解舵机主动运动造成的强迫流量，以及有效地抑制舵机运动干扰。LI等[6]提出了一种新的控制方案，该方案采用流量伺服阀和压力伺服阀并发控制电液负载模拟器，其中流量伺服阀对舵机运动引起的强迫流量进行补偿，能够有效地降低舵机运动带来的干扰，提高了电液负载模拟器的加载精度。

JIAO等[7]对采用结构不变形原理的电液负载模拟系统进行了分析，发现该方法具有不足之处，因此提出了一种新的方法，即采用舵机伺服阀的控制信号作为前馈补偿，实现速度同步控制，以达到更好的控制效果，使它具备相当好的消扰能力和鲁棒性。焦宗夏、华清[8]旨在解决传统控制器鲁棒性差、参数调节复杂和舵机运动干扰的问题，设计了基于RBF神经网络的PID控制器与神经网络补偿器相结合，能够有效地提高电液负载模拟器跟踪精度，并且使系统具有较好的鲁棒性。WANG等[9]提出了一种自适应反步控制器，不仅考虑了抑制舵机运动扰动，而且还考虑了电液负载模拟系统中的非线性特性和参数不确定性，提升了负载模拟精度。JING等[10]提出一种新的鲁棒控制方法，该方法采用奇异扰动理论，实现了电液负载模拟系统的高精度和强鲁棒性。KANG等[11]针对电液负载模拟系统的非线性摩擦和不确定干扰，提出一种基于精确系统模型的有限时间自适应滑模控制方法，提高了加载力的精度和系统的响应速度。何龙飞等[12]提出了一种基于双幂次趋近律的变增益滑模控制，可以有效地降低滑模控制器中抖振问题，从而提高了电液负载模拟器的跟踪精度和系统的响应速度。

滑模变结构控制对参数摄动和外部干扰不灵敏，使系统具有良好的鲁棒性，但这是通过控制量的高频抖动换来的，而这种抖振会影响系统的跟踪精度，所以研究如何消除抖振是滑模变结构控制中一大重点，而模糊控制与滑模控制相结合就是其中一种方法[13]。YANG等[14]为了保证四自由度机器人稳定运动，提出基于递推神经网络的模糊滑模控制，其中采用模糊逻辑系统作为传统滑模控制的切换项，用来降低系统的抖振。SUI 和ZHAO[15]采用自适应模糊滑模控制对光电平台的未知部分进行了估计，并有效地降低了系统的抖振。

从电液负载模拟系统构成的角度来看，目前大多数电液负载模拟器是基于伺服阀工作的。而阀控系统存在节流损耗大、能量效率低等问题[16]。单液压泵控系统虽然可以提高能量效率、降低系统的能耗，但系统的动态特性不如阀控系统。针对以上问题，权龙等人[17-18]提出了双泵分腔调控电液位置驱动方案，并为此设计了双变转速泵的总压力控制策略，以提升系统的刚度和动态性能。

本文作者提出双泵分腔协调控制电液负载的模拟方案，该方案的思路来源于双泵分腔调控电液位置驱动液压缸。围绕该方案建立新型电液负载模拟系统的数学模型、分析系统特性，并采用滑模控制技术设计高性能负载模拟控制器。此外，本文作者还提出一种基于模糊趋近律的等效滑模控制，以解决传统滑模控制中的抖振所引起的跟踪效果不好的问题，并采用李雅普诺夫稳定性分析方法讨论算法的稳定性。最后通过MATLAB/Simulink和AMESim联合仿真手段，验证所提方案和算法的可行性和有效性。

1 系统描述

1.1 双泵分腔调控电液负载模拟原理

双泵分腔调控电液负载模拟系统构成如图1所示。双泵分腔调控电液负载模拟系统通过2个独立的伺服电机控制2个定量泵的转速，以此来控制液压缸两腔的压力和流量。

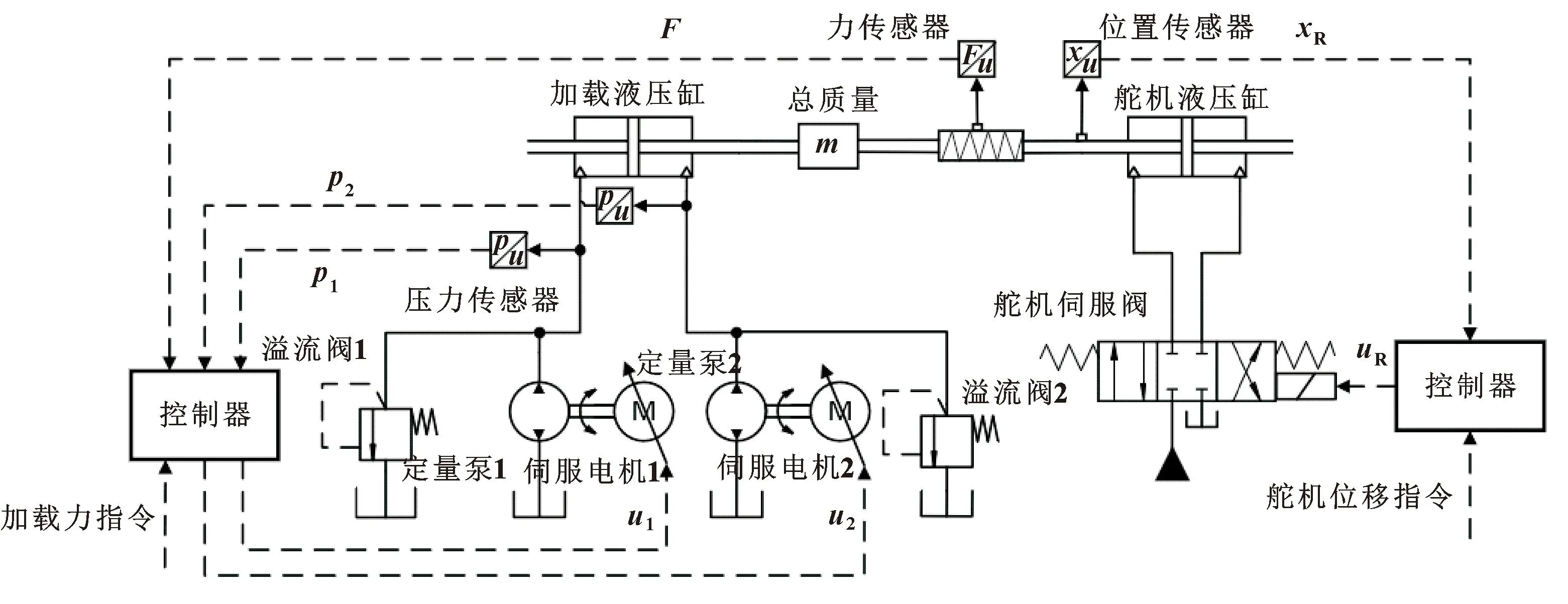
图1 双泵分腔调控电液负载模拟系统构成

1.2 双泵分腔调控电液负载模拟系统数学模型

数学模型的建立基于如下假设：

(1)定量泵与加载液压缸之间的连接管道具有对称性，其管道短而粗，因此能够忽略管道中的压力损失和管道动态；

(2)加载液压缸中每个工作腔内各处压力相等，且加载液压缸的内泄漏为层流流动；

(3)油温和油液体积弹性模量为常数，加载液压缸只有内泄漏，而没有外泄漏；

(4)伺服电机的动态特性远高于液压动力元件(文中为泵控液压缸)的动态特性，可将伺服电机的动态简化成比例环节。

由以上假设，则得伺服电机的转速为

n1=Kau1

(1)

n2=Kau2

(2)

式中：n1、n2分别为伺服电机1、2的转速；Ka为伺服电机的速度增益；u1、u2分别为伺服电机1、2的控制输入电压。

变转速定量泵的流量方程为

(3)

(4)

式中：Q1、Q2分别为流过加载液压缸左、右腔的流量；Dp1、Dp2分别为定量泵1、2的排量；xp为加载液压缸活塞的位移；Cp1、Cp2为定量泵1、2的泄漏系数；p1、p2分别为加载液压缸左、右腔的压力。

加载液压缸两腔流量连续性方程为

(5)

(6)

式中：Ap为加载液压缸活塞的有效面积；Cip为加载液压缸的内泄漏系数；βe为油液体积弹性模量；V1为加载液压缸左腔的容积；V2为加载液压缸右腔的容积，且V1=V2=Vt/2，Vt为加载液压缸总容积。

加载液压缸的力平衡方程为

(7)

式中：m为加载液压缸活塞和舵机液压缸活塞折算到活塞杆上的总质量；Bp为加载液压缸黏性阻尼系数；F为加载力；fF为未建模的摩擦力。

加载力的表达式为

F=K(xp-xR)

(8)

式中：K为力传感器的弹簧刚度；xR为舵机液压缸活塞的位移。

sgn(x)为一个不连续的符号函数：

(9)

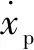
(10)

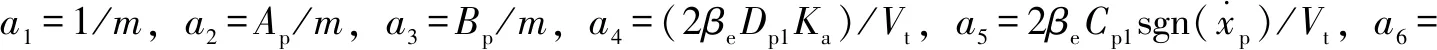
2 控制策略和控制器设计

控制策略和控制器设计过程基于以下假设：

(1) 参数βe、Cp1、Cp2在系统运行过程中不变；

(2)加载力参考指令和舵机位移参考指令3阶可导。

2.1 控制策略的设计

为了提高泵控系统特性，使双泵分腔调控电液负载模拟系统能够和阀控系统有类似的特性，文中借鉴阀控缸系统中液压缸两腔压力和为定值，且在工作时两腔压力反向变化，产生压差驱动液压缸活塞运动的原理，在双泵分腔调控电液负载模拟系统中采用力-总压力复合控制策略如图2所示。

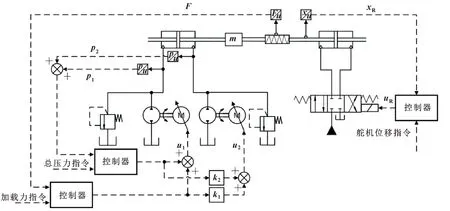
图2 力-总压力复合控制策略

该策略的原理是2个变转速定量泵的转速信号均由1个力控制环中控制器输出信号和1个总压力控制环中控制器输出信号2部分组成，2个变转速定量泵的转速信号为

n1=n1F+n1p

(11)

n2=n2F+n2p

(12)

式中：n1F和n2F分别为加载力指令和力传感器信号经过控制器后得到的变转速定量泵1、2的转速信号；n1p和n2p分别为总压力指令和压力传感器信号经过控制器后得到的变转速定量泵1、2的转速信号。

在不考虑液压泵泄漏、加载液压缸泄漏和油液压缩时，结合式(3)—(6)和式(11)(12)可得：

(13)

(14)

联立式(13)(14)可得：

(15)

由于加载液压缸工作时，1个腔室进油，另1个腔室出油，这会导致加载液压缸2个腔室的体积朝相反方向变化，则2个变转速定量泵的转速始终相反，故力控制环中k1为

(16)

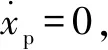
Dp1n1p=Cp1p1

(17)

Dp2n2p=Cp2p2

(18)

定义负载压力为

pL=p1-p2

(19)

设置加载液压缸两腔的压力和p∑为定值，则：

p∑=p1+p2

(20)

联立式(19)(20)可解得：

(21)

(22)

将式(21)(22)代入式(17)(18)得：

(23)

(24)

联立式(23)(24)，并将条件pL=0代入可得总压力控制环中的k2为

(25)

由于2个变转速定量泵的参数相同，则将式(1)(2)(16)(25)代入式(11)(12)可得：

(26)

2.2 力控制环中控制器设计

2.2.1 基于指数趋近律的等效滑模控制器的设计

定义加载力指令信号为x1d，则加载力跟踪误差e为

e=x1-x1d

(27)

针对系统的状态空间方程，定义滑模函数s为

(28)

式中：c1、c2必须满足Hurwitz条件，即c1=λ2，c2=2λ，λ>0。

文中设计的滑模控制器由等效控制u1eq和趋近律控制u1zs两部分组成，即：

u1F=u1eq+u1zs

(29)

(30)

其中，干扰d为

(31)

式中：|d|≤D，D∈(0,+∞)。

当不考虑干扰，即d=0时，则等效控制u1eq为

(32)

文中采用指数趋近律，则趋近律控制为

(33)

式中：ks1>0；ks2>0。

2.2.2 模糊控制控制律的设计

指数趋近律中的指数趋近项可以使系统状态以较快的速度趋近于滑模动态，提高系统的响应速度；而指数趋近律中的等速趋近项能保证滑模控制的鲁棒性，但滑模控制的抖振也是由等速趋近项造成。因此，可采用模糊规则对等速趋近项进行模糊化，降低系统的抖振。

基于模糊趋近律的等效滑模控制律设计如下：

(34)

通过模糊系数μ将指数趋近律中的等速趋近控制模糊化，这样既能保证系统具有较高的响应速度，又能有效地降低抖振。

定义模糊滑模控制器输入输出的模糊集均对应负(N)、零(Z)、正(P)。模糊滑模控制输入s的论域为：s=[-2×108，2×108]，模糊输出μ的论域为：μ=[-1，1]。

模糊系统的输入和输出隶属函数如图3所示。

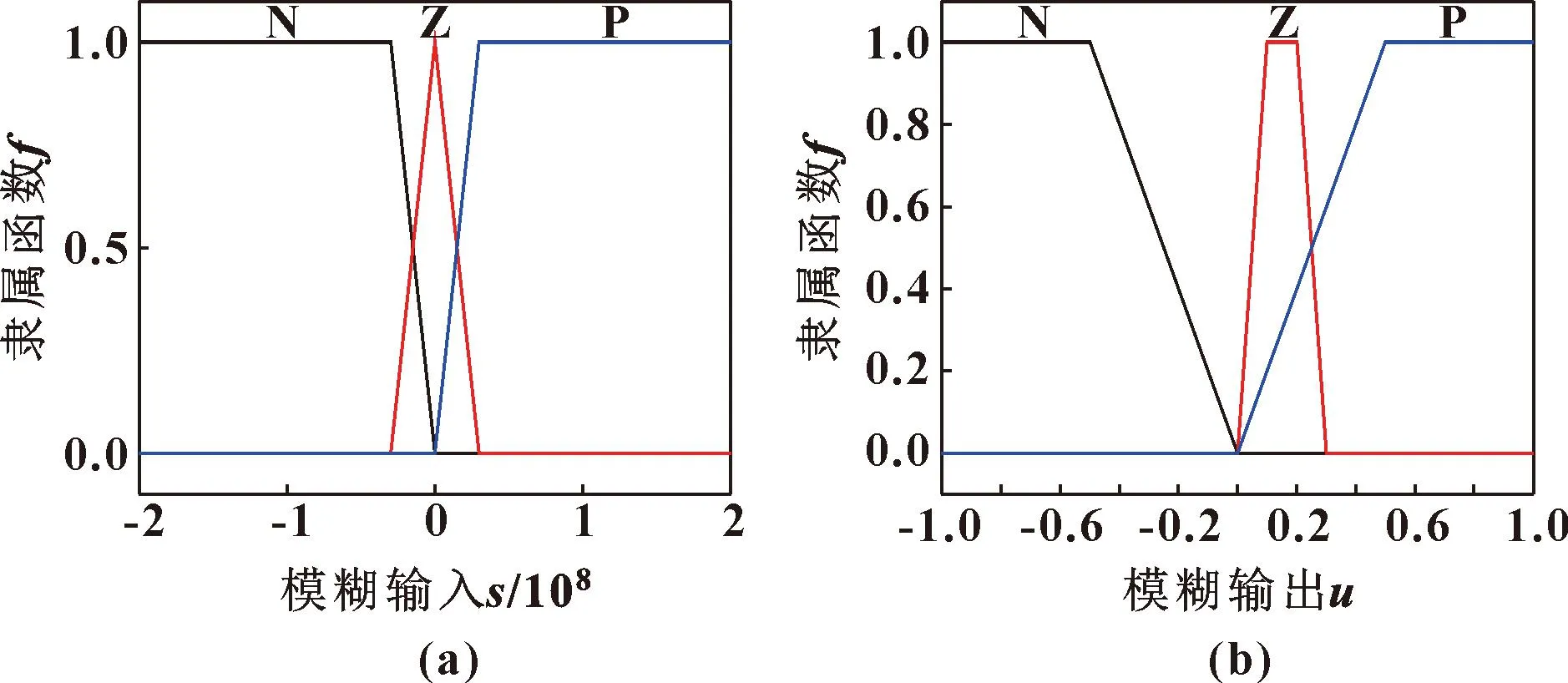
图3 模糊输入s (a)和模糊输出μ(b)的隶属函数

其模糊规则表示为

Ifs(t) is N thenμis P

(35)

Ifs(t) is Z thenμis Z

(36)

Ifs(t) is P thenμis P

(37)

式(35)(37)中“当μ≠0时，表示系统有干扰，且μ始终大于0”，此时控制律由等效控制项、等速趋近项和指数趋近项构成。当模糊输入s较小时，可通过模糊输出μ实现等速趋近项中ks1的模糊化，保证在补偿干扰的同时，能有效地降低由于等速趋近项过大而引起的抖振。

模糊系统采用重心法进行反模糊化。模糊输入、输出的隶属函数如图3所示。

定义Lyapunov函数为

(38)

结合式(28)(29)(34)可得：

-s(μks1sgn(s)+d)-ks2s2

(39)

则式(39)为

(40)

因此，文中设计的基于模糊趋近律的等效滑模控制器下的系统是稳定的。

3 仿真研究

通过MATLAB/Simulink和AMESim联合仿真平台，搭建一个基于双泵分腔调控电液负载模拟系统的联合仿真模型。其中，在AMESim仿真软件中搭建液压系统模型，在MATLAB/Simulink仿真软件中搭建基于模糊趋近律的等效滑模控制器模型。在仿真模型中，文中考虑了泵的泄漏、液压缸的内泄、静摩擦、库仑摩擦、黏性摩擦等对系统的影响。联合仿真模型如图4所示。

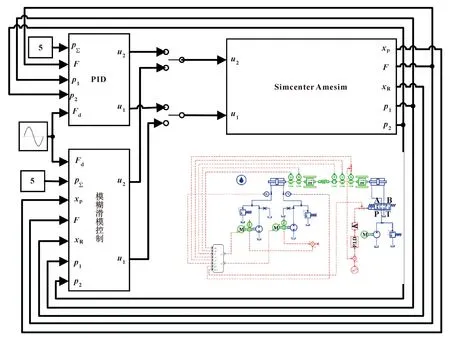
图4 联合仿真模型

表1为液压仿真模型的主要参数，而联合仿真的采样时间设置为0.01 s。总压力的参考指令为：pΣ=5 MPa，且总压力控制环中控制器采用PID控制器。

表1 液压仿真模型参数

为了验证所设计的力-总压力复合控制策略的可行性和有效性，将所设计的双泵分腔调控电液负载模拟系统(后续简称“双泵”)与单伺服阀控制电液负载模拟系统(后续简称“单阀”)和单闭式变转速泵控制电液负载模拟系统(后续简称“单泵”)做对比；仿真过程中，液压仿真模型参数都是一致的。

所设置的加载力参考指令为Fd=10 000×sin(2πt)N，舵机位移参考指令为xR=0.01×sin(2πt) m。3个系统中的控制器均采用PID控制器，其中单泵系统中PID控制器参数为：KP=1，KI=40，KD=0；双泵系统中PID控制器参数为：KP=2，KI=80，KD=0；单阀系统中PID控制器参数为：KP=0.01，KI=0.35，KD=0。3个系统的加载力跟踪效果以及加载力跟踪误差如图5、6所示。为了更清晰地了解单阀系统能耗高的问题，与双泵系统进行对比，如图7所示。

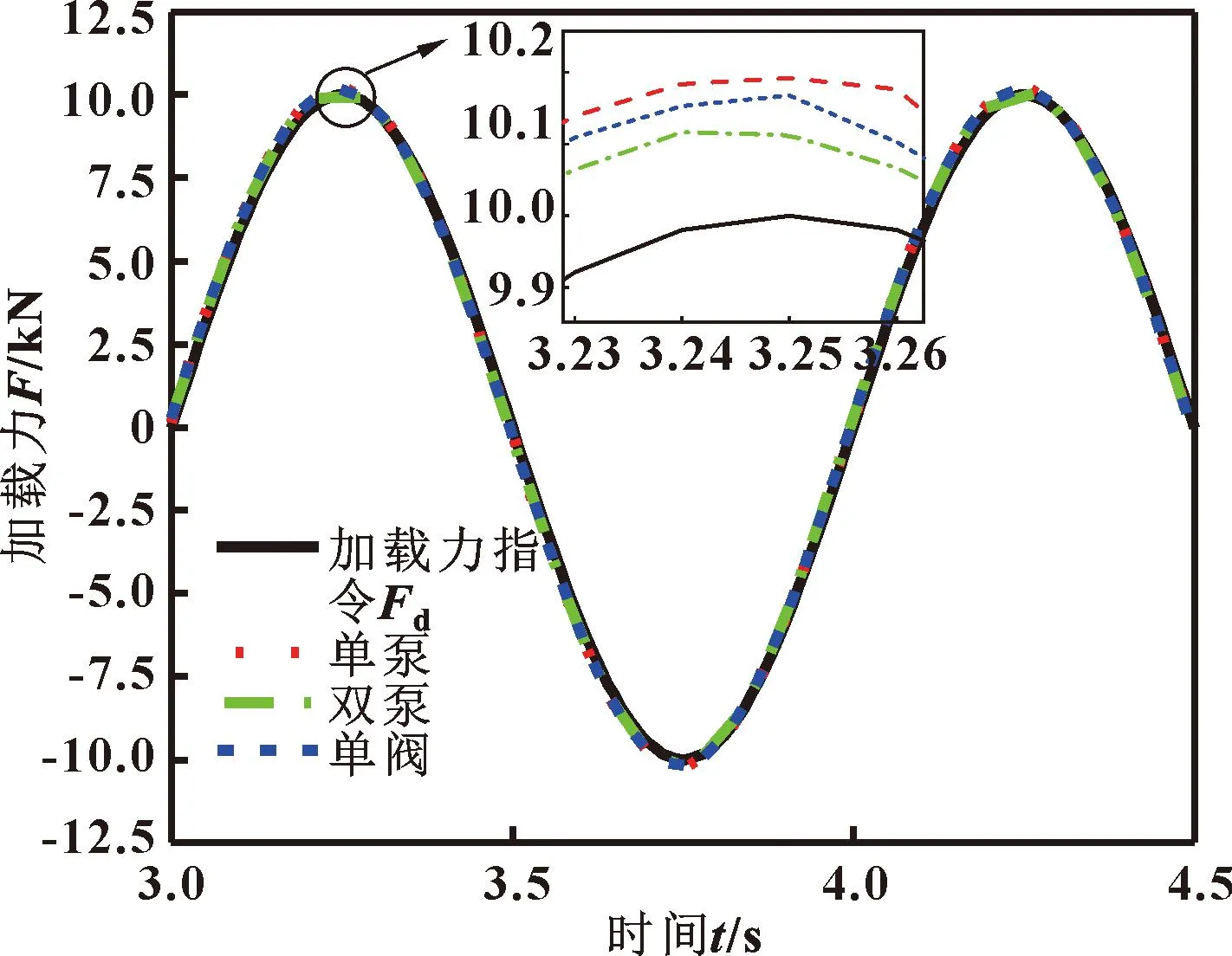
图5 不同系统加载力跟踪效果对比

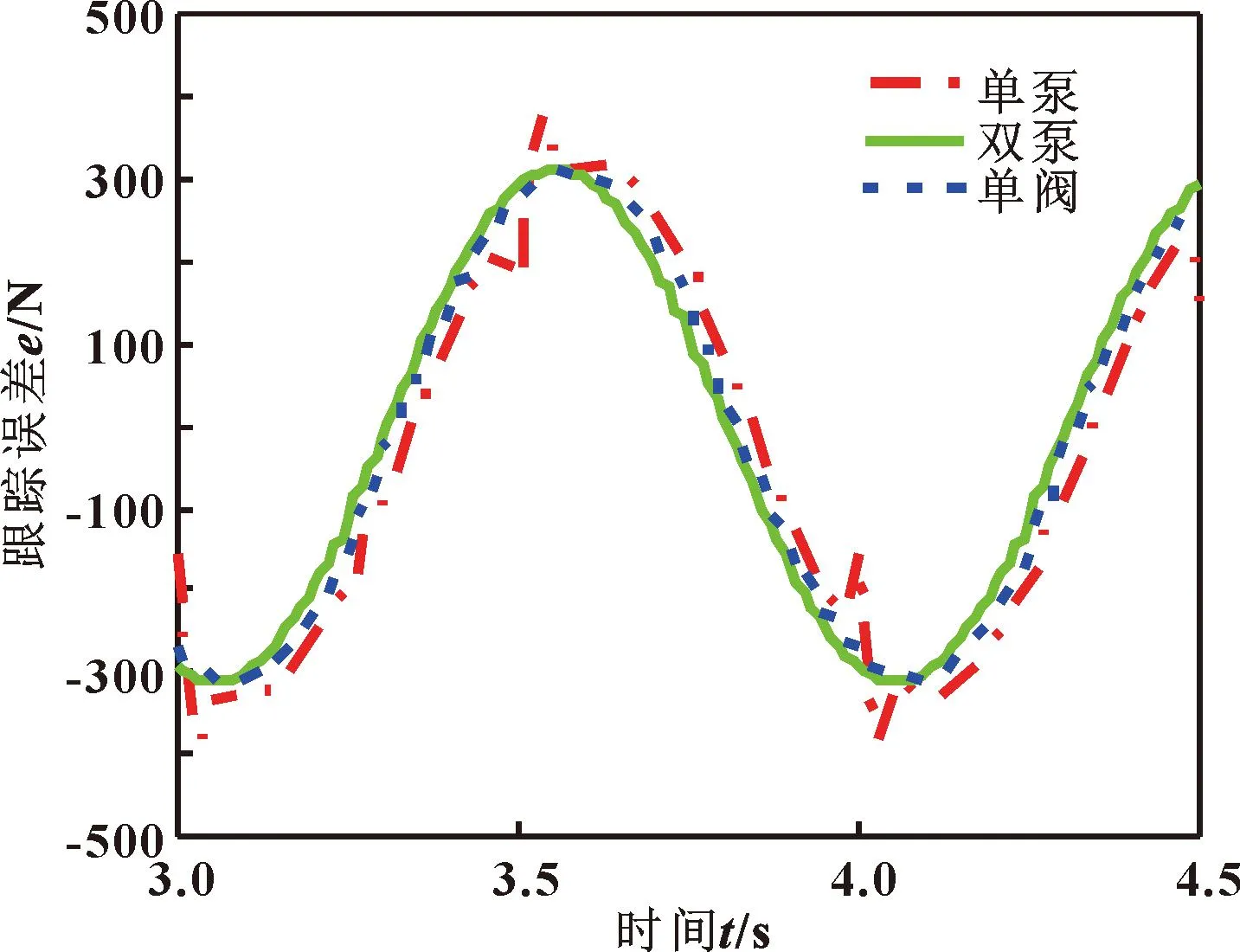
图6 不同系统加载力跟踪误差对比

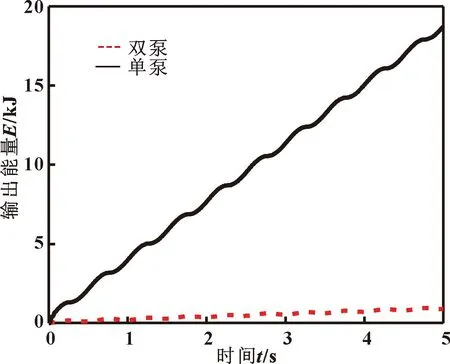
图7 双泵系统和单阀系统能耗对比

由图5、6可知：在仿真过程中，双泵系统和单阀系统的加载力跟踪效果较好，单泵系统的加载力跟踪效果较差，表明设计的力-总压力复合控制策略具有可行性，且效果良好。由图7可知：双泵系统在5 s内能量总消耗876.8 J，相比于单阀系统在5 s内能量消耗18 725.8 J，减小了95.3%。

为了定量分析控制器的控制性能，定义以下3个参数：

(41)

(42)

(43)

式中：e(i)为第i次采样时的加载力跟踪误差；N为总的采样数据个数；u(i)为第i次采样时的控制输出；IAPE为稳态时最大跟踪误差绝对值，IAPE越小，控制器的控制性能越好；IRMSE为稳态时跟踪误差的均方根值，反映加载力信号偏离加载力参考指令的程度，IRMSE越小，控制器的控制性能越好；IRMSU为稳态时控制输出的均方根值，IRMSU能反映控制器的输出强度。

根据所定义的参数，3个系统的控制器性能指标如表2所示。

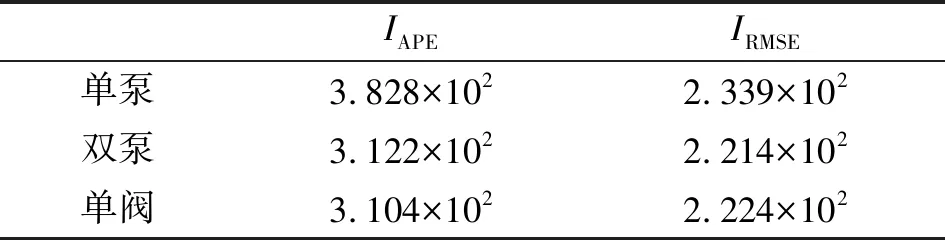
表2 三个系统的控制器性能指标

由表2可知：3个系统中双泵系统加载精度最高，单阀系统加载精度次之，单泵系统加载精度最差。相比单泵系统的加载精度，双泵系统和单阀系统加载精度相近，而双泵系统的总能耗远低于单阀系统的能耗，所以双泵分腔调控电液负载模拟系统结合阀控系统和泵控系统的优点，使系统在长时间的加载工况下，不仅能保证良好的跟踪精度，也能节约大量的能量消耗。

针对式(34)中的参数ks2和μ，分3种情况进行仿真对比：

(1)当ks2=0且μ=1时，此时力控制环中控制器为传统的等效滑模控制，记控制器为u1A=u1eq-ks1sgn(s)/Ka2a4。

(2)当ks2=0且μ≠1时，此时力控制环中控制器为基于等效控制的模糊滑模控制，记控制器为u1B=u1eq-μks1sgn(s)/Ka2a4。

(3)当ks2≠0且μ≠1时，此时力控制环中控制器为基于模糊趋近律的等效滑模控制，记控制器为u1C=u1eq-ks2s/Ka2a4-μks1sgn(s)/Ka2a4。

为了验证基于模糊趋近律的等效滑模控制器的可行性和有效性，对3个控制器进行对比分析，如图8、9所示。

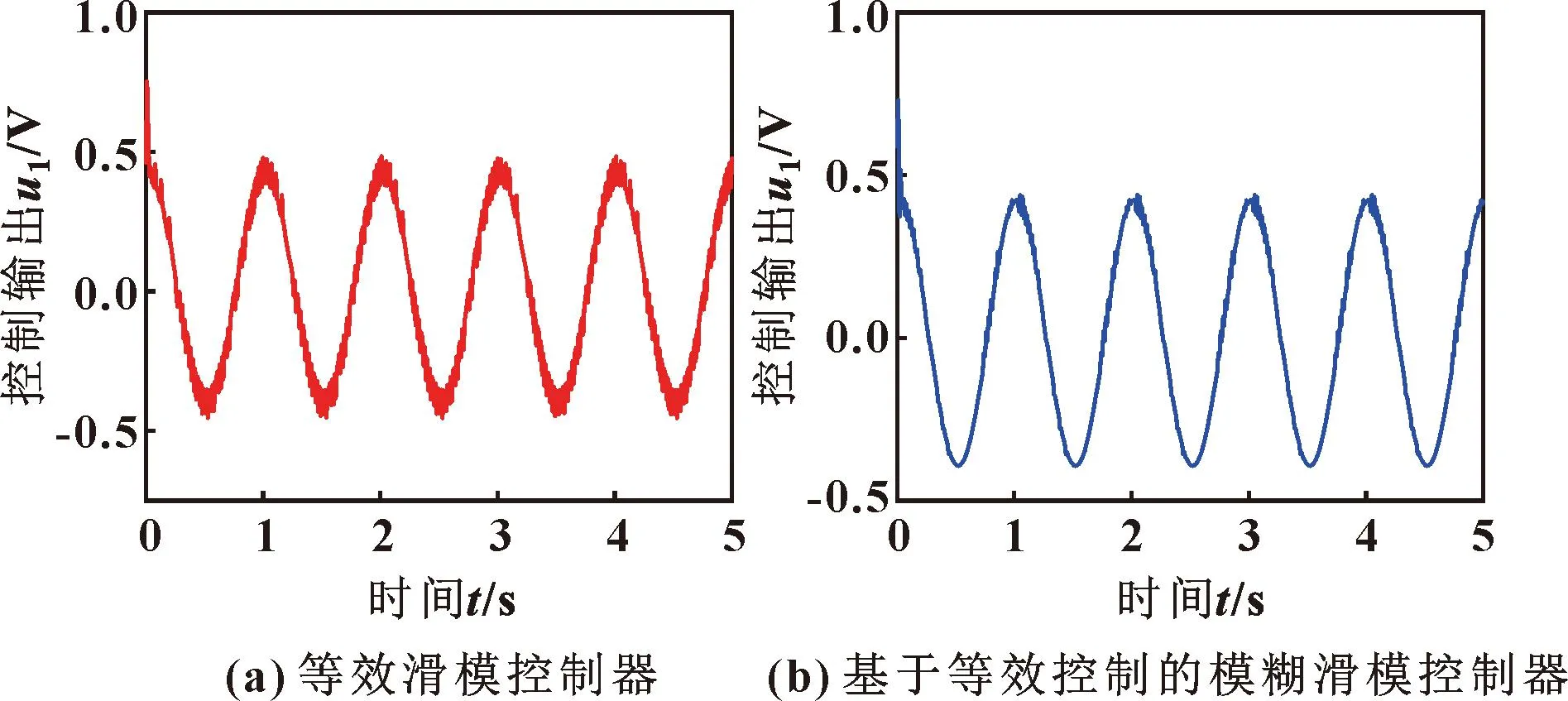
图8 控制输出曲线

由图8可知：当加载力参考指令为Fd=10 000×sin(2πt)N、舵机位移参考指令为xR=0.01sin(2πt)m、双泵系统分别采用控制器u1A和u1B时，对比2条控制输出曲线可得，系统采用基于等效控制的模糊滑模控制器u1B能有效地抑制系统抖振。

由图9可知：当加载力参考指令为Fd=10 000 N、舵机位移参考指令为xR=0.01sin(2πt) m时，双泵系统采用控制器u1B时，其上升时间为0.269 s；而采用控制器u1C时，其上升时间为0.046 s，与控制器u1B相比，上升时间减小了82.9%。可见，加入指数趋近项的基于模糊趋近律的等效滑模控制器u1C显著提高了系统的响应速度，特别适合用于大阶跃的加载指令。

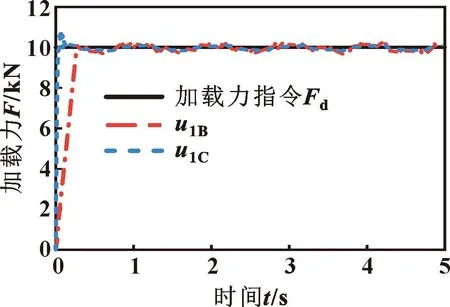
图9 不同控制器跟踪结果对比

设置加载力参考指令为Fd=10 000sin(2πt)N、舵机位移参考指令为xR=0.01sin(2πt)m，2个控制器的加载力跟踪对比与控制输出对比分别如图10—12所示。可知：在考虑了系统的非线性摩擦和舵机运动等干扰情况下，双泵系统采用控制器u1A时，虽然能很好地跟踪加载指令，但由于等速趋近项中ks1值过大，从而造成系统抖振，会影响系统的加载精度；而双泵系统采用控制器u1C时，由于模糊输出μ对等速趋近项进行了模糊化，显著降低了系统的抖振。

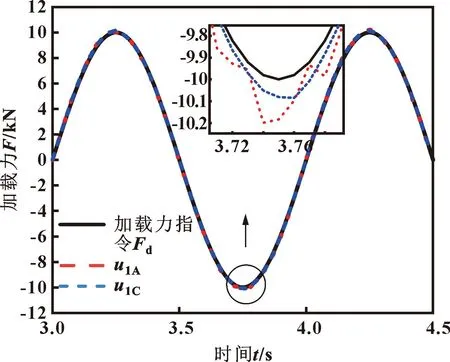
图10 不同控制器加载力跟踪对比

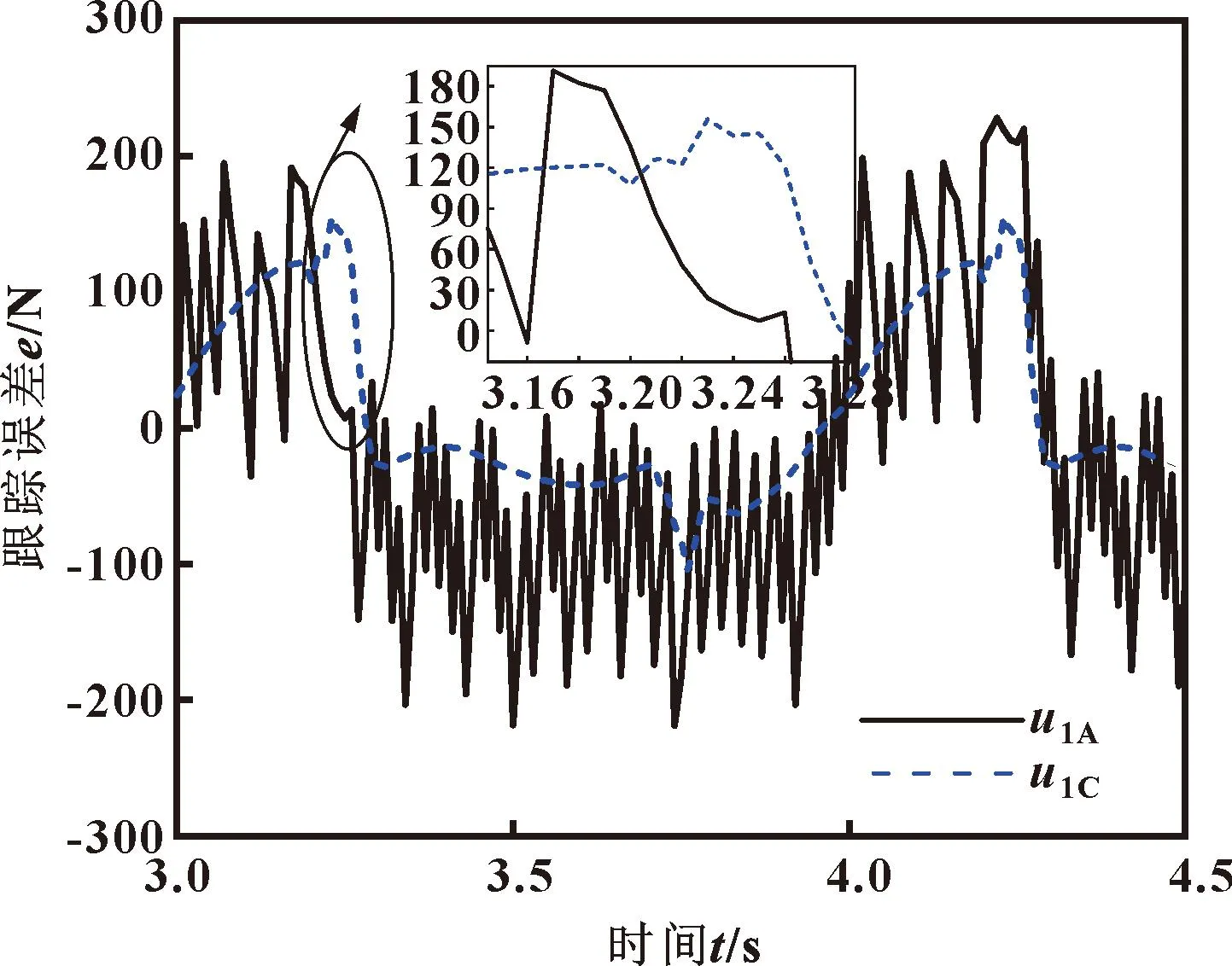
图11 不同控制器跟踪误差对比

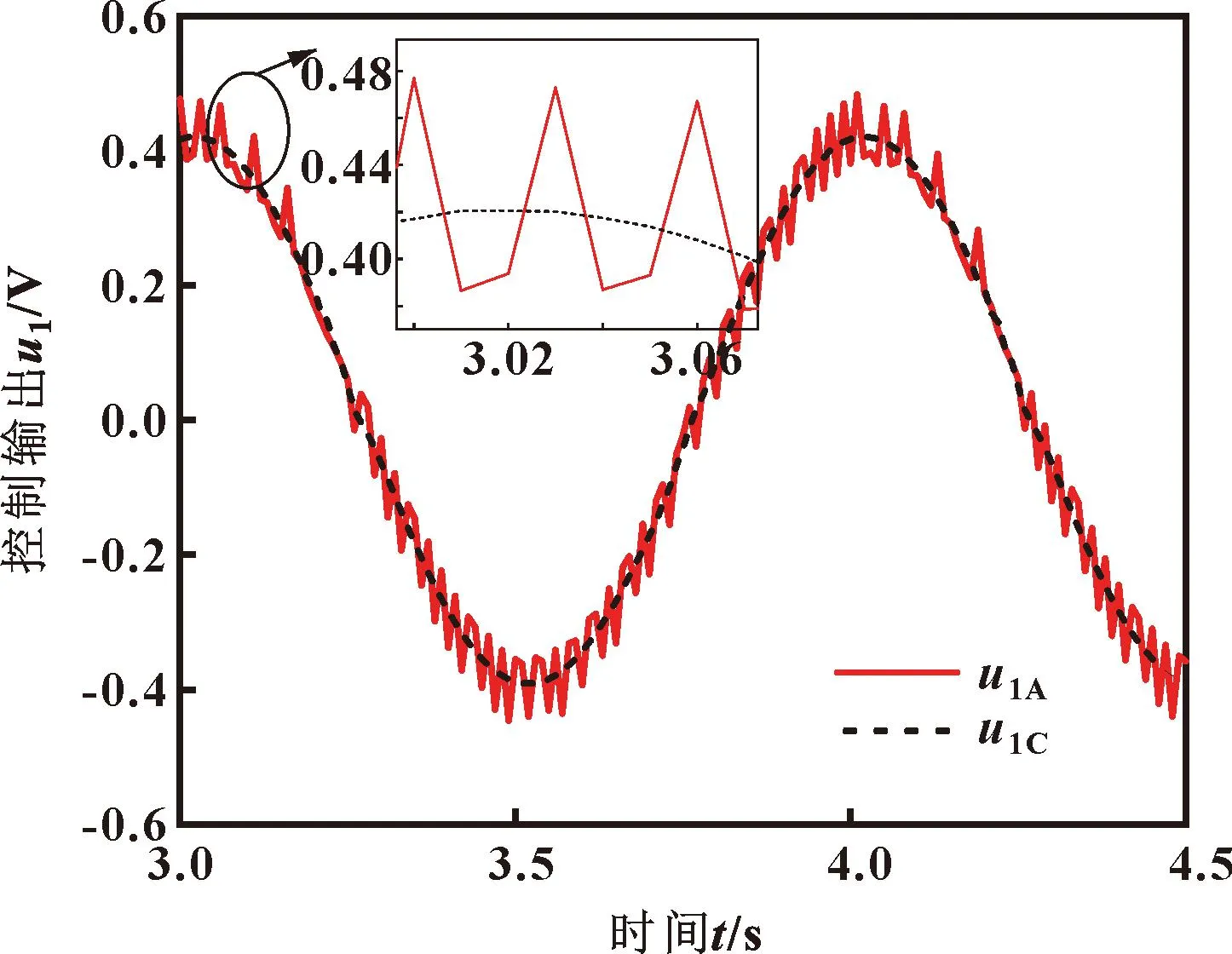
图12 不同控制器控制输出对比

根据所定义的参数，2个控制器的控制性能指标如表3所示，可定量地分析双泵系统的加载精度。

表3 不同控制器的控制性能比较

由表3可知：控制器u1C的IAPE和IRMSE参数值明显比控制器u1A的小，其参数值分别降低了31.8%和41.0%，同时控制器u1C的IRMSE参数值是2个控制器中的最小值。因此，在控制器输出强度相近时，基于模糊趋近律的等效滑模控制器u1C的控制性能显著优于等效滑模控制器u1A，即当双泵分腔调控电液负载模拟系统中的控制器采用基于等效控制的模糊滑模控制器u1C时，能显著地提高系统的加载精度。

4 结论

(1)与单泵控电液负载模拟系统和单阀控电液负载模拟系统相比，双泵分腔调控负载模拟系统中采用力-总压力控制策略，不仅可以保证较高的加载精度，也能显著降低系统能耗。

(2)与传统的等效滑模控制器相比，基于模糊趋近律的等效滑模控制器能有效地降低抖振，且采用该控制器的双泵分腔调控负载模拟系统响应速度提高了82.9%。

(3)与传统的等效滑模控制器相比，基于模糊趋近律的等效滑模控制器的控制效果提升了41.0%。