多维注意力机制神经网络在电力工程数据中的应用研究
王琼,吕征宇,薛礼月
(国网上海市电力公司经济技术研究院,上海 200233)
电力工程建设具有投资金额大、建设周期长的特点,而造价管理是相关工程管理工作中的重点内容[1-4]。电力工程造价数据具有多变量及非线性等特征,但传统的电力工程造价仅依靠人工核算的方法,管理人员通常根据工程平面图和相关报价进行计算,数字化程度较低。同时,现代电力工程的发展也使得人工核算方法的局限性被不断放大[5-6]。因此,使用数字化与自动化的手段对相关投资行为进行合理、科学的管理及预测是未来的发展趋势。
在其他领域,例如电力负荷预测、电力系统故障预测中,通常采用人工智能的相关算法,预测准确度较高。而电力造价数据从属性的角度来看与这些领域基本一致,均具有高维度、非线性及时序性等特征。因此,文中使用多维注意力神经网络对电力工程数据进行分析,并提取数据的多维度特征,进而实现对数据的分析与预测。
1 电力工程数据处理模型设计
1.1 多尺度卷积神经网络结构设计
卷积神经网络(Convolutional Neural Networks,CNN)[7-9]是一种前馈多层神经网络,一维卷积神经网络由输入层、卷积层、池化层、全连接层和输出层组成。其中,输入层与输出层完成数据的输入、输出,卷积层及池化层对输入信号进行卷积和池化运算,最终通过全连接层获取数据的分类结果。CNN 网络的结构如图1 所示。

图1 CNN网络结构
文中所采用的卷积层由一维卷积核组成,每个卷积核均对输入信号的域进行卷积运算。卷积运算的过程如下所示:
式中,l为卷积核数;Xi为第i层的特征向量;wij表示第i层卷积的第j个卷积权重值;bj表示第j个偏置值;f(·)为激活函数;Xj为卷积输出值。激活函数的作用是将输入数据完成从非线性到线性的映射。常用的激活函数为tanh 函数,其计算公式为:
该文将池化层部署在多个卷积层之间,主要作用是对卷积层的高维数据进行降维,并对卷积得到的结果加以简化,进而减少计算参数。池化过程可表示为:
式中,βj表示权重值;bj表示偏置值;D(·)表示采样函数。
全连接层可以将本层神经元与前一层神经元相连接,进而实现从特征数据到最终输出的映射,再通过分类函数完成最终的输出。文中通过用Softmax函数获得分类结果,该函数可表征为:
式中,zi为第i个卷积核的输出值;C为输出卷积核的个数,其对应的数据即为分类类别的数量。
输入数据经过卷积神经网络的各层最终输出,随着通道数的增加,特征向量不断变小,而不同尺寸的卷积核对数据的筛选能力也有所不同。因此,对多种不同尺寸的卷积核进行合理组合可以全面提升CNN网络的特征提取能力。在多尺度CNN中,每个层的卷积层均由不同大小的卷积模块组成,如图2 所示。
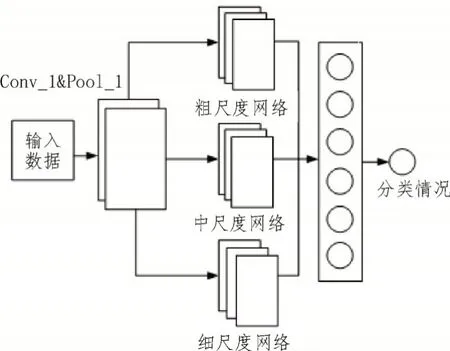
图2 多尺度卷积神经网络
该文采用的多尺度网络主要参数如表1 所示。
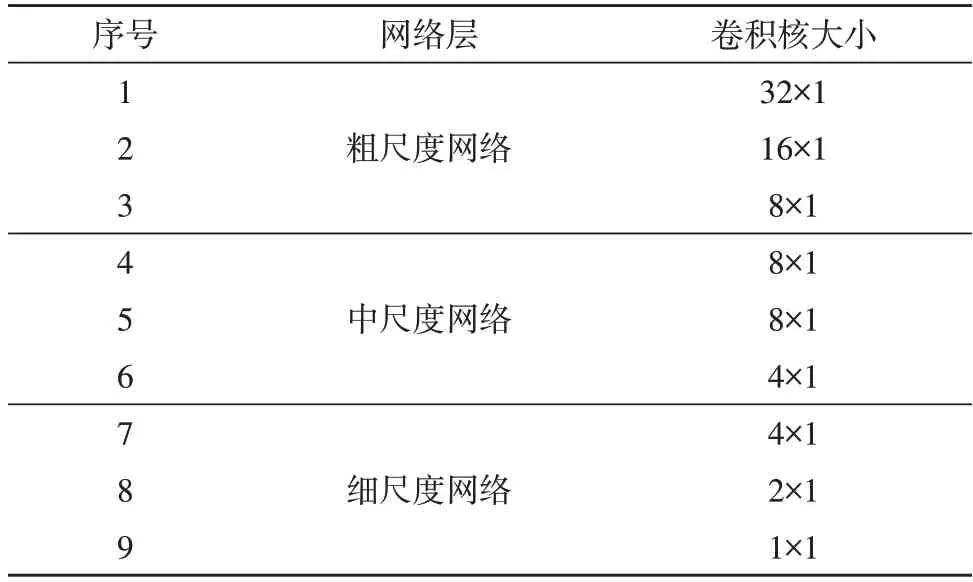
表1 多尺度卷积神经网络主要参数
1.2 残差网络优化
虽然多尺度卷积网络相较于一维神经网络在训练准确度方面有所提高,但随着网络层数的不断增加,训练的计算开销也会持续提升,而模型的鲁棒性和抗噪性则会进一步下降。因此,需要对多尺度卷积网络加以改进,文中选择残差网络(Residual Network,ResNet)[10-13]来进行改进。
残差网络是一种多层次网络间的快速链接方式,该网络并未对多个网络的映射关系进行分析,而是直接映射残差网络自身与网络的关系,使原始输入信息可以无损传递到后续的输出层中,且通过层与层之间相连,进而有效解决网络收敛及梯度消失等问题。该文采用的ResNet 网络结构如图3 所示。

图3 ResNet网络结构
可以看到,ResNet 网络以残差单元为主要组成结构,可将多个残差结构进行堆叠。当输入数据为x时,残差结构的输出则为F(x)+x,F(x)则为原网络的输出。
虽然ResNet 网络可以在一定程度上解决一维卷积网络存在的问题,但其存在参数过大的弊端,因此仍需对ResNet 网络进行简化,以降低数据过拟合的风险。文中将原始的二维ResNet 网络降为一维网络,从而达到简化网络、实现特征网络重复利用的目的。更改后的ResNet 网络与多尺度网络结合的简化结构如图4 所示。

图4 优化ResNet网络结构
从图4 可知,优化后的ResNet 网络被放置在大尺度卷积中。由于小尺度卷积核提取的多为局部特征,其所包含的时序特性是短期的;而深层网络使用的大尺度卷积全局性较强,包含的时序特征则是长期的。因此将局部和全局特征相连接,并将残差网络放置在大尺度卷积中,进而使模型获得更为全面的特征信息,同时还可提升模型的运算速度。
1.3 卷积块多头注意力机制
多头注意力机制(Multi-Head Attention)[14-16]是一种并行注意力机制,其可使输入数据的编码能力大幅提升。该机制使用矩阵对原始注意力机制中的Q、K、V三种向量进行映射,同时对原始数据完成多次注意力操作,之后再进行合并。执行过程如下:
式中,Wi表示权重矩阵,fattention表示注意力拼接函数。
输入数据经由残差网络后,会得到海量的数据特征,为了对这些特征进行分类,在残差网络后加入多头注意力模块,该模块是对单个卷积中注意力模块的拼接。设计的单个卷积注意力模块的结构如图5所示。
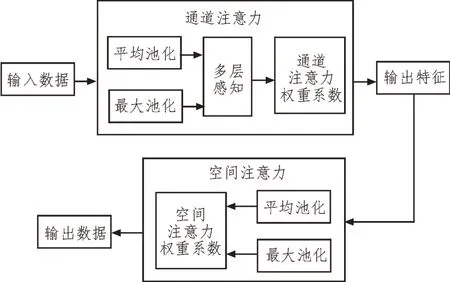
图5 单个卷积块注意力模块的结构
图5 中,注意力机制分为通道注意力模块和空间注意力模块。假定输入特征向量为X,则卷积块注意力机制会沿着通道和空间构建两种不同的输出特征,如下所示:
式中,X″为最终输出结果,⊗为张量积运算。通道注意力的计算方式为最大池化和平均池化,计算公式为:
式中,使用ReLU 作为总的激活函数,σ则表示Sigmoid 函数。
空间注意力也是通过两个池化来完成的运算过程:
1.4 MultiATT-CNN模型设计
文中最终模型由上述改进的多尺度卷积神经网络、残差网络以及多头卷积注意力机制组成。该模型首先通过大尺度的卷积核获取数据的全局特征,进而得到多尺度的残差网络;然后,将残差网络结构放置于粗尺度网络与细尺度网络之间;最后再放置多头注意力机制,并通过全连接层得到最后的预测结果。MultiATT-CNN 算法模型结构如图6 所示。

图6 MultiATT-CNN算法模型结构
2 实验测试
2.1 算例数据及运行环境
文中算例数据集来源于国家电网中的电力基建工程数据,数据获取软件为D-Grid 基建管理平台。数据可分为5 个类型,具体如表2 所示。同时使用Python3.7 编写算法代码,并将TensorFlow 作为深度学习框架。硬件配置如表3 所示。

表2 数据分类信息

表3 实验配置信息
2.2 仿真结果分析与对比
在仿真测试前,还需要对模型的仿真参数进行确定。对深度学习而言,迭代次数的选择极为关键,次数过多容易使模型陷入梯度消失的风险,次数过少则会导致准确度降低。因此,首先对迭代次数进行了仿真,实验结果如图7 所示,设定迭代次数为11 次。

图7 迭代次数仿真结果
在仿真测试中,首先进行消融实验,验证所提改进模型与原始模型的差异。对比算法为CNN、多尺度CNN、多尺度CNN-ResNet。算法数据中的训练集选择2016—2020 年的基建投资数据,验证集为2021年的数据,评价指标则为平均预测准确率及运行时间。消融实验测试结果如表4 所示。

表4 消融实验测试结果
由表4 可知,在添加了残差网络以及注意力机制后,算法的预测准确度会逐渐提升。而多尺度CNN 算法由于采用了多个尺度和数量的卷积核,相较原始算法其运行时间有所增加,但在加入残差结构后,运行时间减少了约4 s。
在横向算法测试中,文中使用同类型算法进行了对比仿真测试。对比算法选择LSTM、XGBoost、BP 神经网络和随机森林算法,评价指标为平均预测准确率及算法运行时间。最终的测试结果如表5所示。
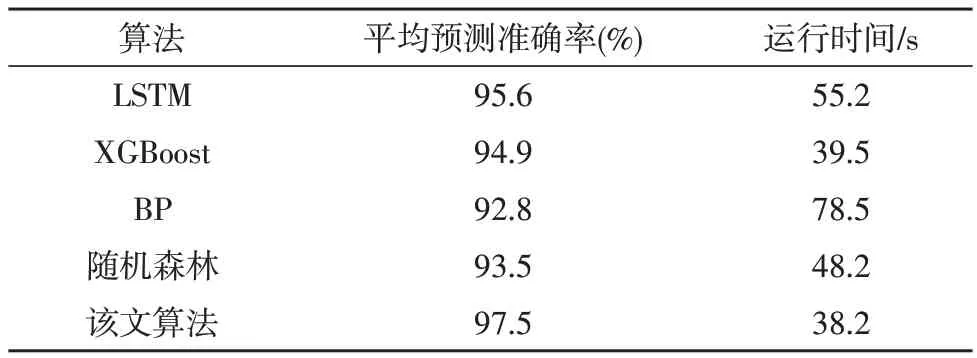
表5 横向算法测试结果
从表5 中可以看出,该文算法的平均预测准确率在所有算法中最高,同时由于算法中加入了可以缩短运行时间的残差网络,因此其在对比算法中的运行时间也最低。这说明该文算法具有良好的性能及效率,鲁棒性及工程适用性均较高。
3 结束语
文中基于改进神经网络提出了一种电力工程造价数据的分析算法。在对CNN 进行改进的基础上,采用多尺度卷积核提升模型的全局感知能力,同时使用残差网络增加模型的训练速度,利用多头注意力机制增强了模型的编码能力。测试结果表明,该文算法相较于对比算法具有更高的准确率及更快的运行速度,说明其工程应用能力较优。

