基于自然驾驶数据的驾驶换道风格分析与辨识
刘志强,马进
(江苏大学汽车与交通工程学院,江苏镇江 212013)
近年来有许多通过采集驾驶数据并通过处理后用于驾驶风格的分析与识别。李经纬等[1]运用K-means 算法对驾驶员风格进行识别。吴振昕等[1]利用K 均值和D-S 证据理论决策融合分析搭建了驾驶人识别模型。彭金栓等[2]选取风险感知因子与临界安全系数为参数构建行人风格识别模型。李立治等[3]基于神经网络建立的驾驶识别模型。刘志强等[4]基于驾驶人数据建立起随机森林模型对跟车行为和识别。然而,通过以上建立模型方法对数据的特征提取和分析来确定换道过程中的关键特征却很少,且缺少相似模型的验证和对比。
该文通过统计分析和时频分析各驾驶员的换道因素,得到输入参数并建立基于改进的PSO-SVM 的驾驶人风格辨识模型。为驾驶辅助系统的发展提供有力支持。
1 数据采集与处理
1.1 数据集介绍
该文使用下代仿真(Next Generation Simulation,NGSIM)[5]数据集。NGSIM 的子集US-101 数据集是来自于美国101 号高速公路的车辆轨迹数据,路段车辆轨迹数据的采集间隔时间精度为0.1 s。路段由5条主路车道、1 条集散车道构成,为避免堵塞,选取US-101 路段08:05-08:35 时轨迹数据为宜。
1.2 数据预处理
1.2.1 数据清洗和处理
通过Kalman 滤波[6]对采集数据进行清洗处理,主要对车辆横向位置、速度以及加速度等换道数据进行处理,以1391 号车辆为例,车辆滤波降频后对比如图1 所示。

图1 1391号车辆滤波降频后对比
1.2.2 数据提取
实验所提取数据为车辆行驶过程中轨迹数据,具体包括:换道时间、速度、加速度、跟车时距、与前车相对距离等[7];上述提取参数能较为全面地反映驾驶人换道驾驶行为特性,换道特征参数如表1 所示。

表1 换道特征参数
2 驾驶员风格分类
2.1 聚类结果
该研究运用K-means 聚类[8]对每位驾驶人换道特征参数进行聚类,可将数据中所采集驾驶员分为激进型、一般型和谨慎型三种风格。激进型、一般型和谨慎型的比例约为2∶7∶5,结果如表2 和图2 所示。

表2 K-means聚类结果
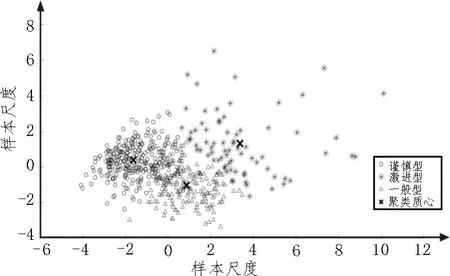
图2 聚类结果
2.2 聚类参数分析
1)统计分析
对聚类参数进行统计分析,参数为换道时间、速度、加速度、跟车时距、与前车相对距离的均值,标准差,最大、最小值,其中对有明显差异的参数进行方差检验,对无显著差异的使用K-W 进行检验。统计分析的均值,标准差,最大、最小值的计算公式如下:
其中,i为单独样本;xi为换道各样本参数,n为总样本数。
K-W 检验公式如下:
其中,N是样本量;Rj是秩和;nj是其测量值;J是样本组数。
换道时间、速度、加速度、跟车时距、与前车相对距离的均值(95%置信区间内)如表3 所示。
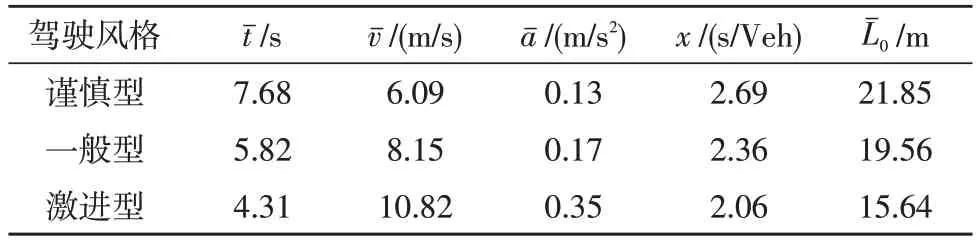
表3 聚类后换道参数分析
从表3 中得到,驾驶人从谨慎型到激进型的平均换道频次逐渐下降,其中,激进型驾驶员换道行为更趋于快速完成,且换道时间更短,而谨慎型驾驶人换道时的行为数据相反;再者,驾驶人的平均速度与平均加速度呈上升趋势,可以说明激进型驾驶员的操稳因子和加速因子较大,谨慎型驾驶员反之。最后,驾驶人的平均车头时距和平均初始与前车相对距离逐渐下降,说明激进型驾驶员更迫切地提前换道,安全性低,谨慎型驾驶员则反之。将统计结果进行K-W检验,发现v和x0的中位数差异显著,各是0.023 和0.532,大于0.01,没有明显差异,其他指标都小于0.01,存在差异性,可以看出不同驾驶人的驾驶风格有明显不同并且符合客观事实,可用于下一步驾驶风格辨识模型的建立。
2)小波时频分析
小波变换[9]可对信号的时频进行精细化处理,如信号f(t),r0为被测小波起点,则其级数展开如下:
其中,r是尺度;t是时间;s是位移,cr0(s)是近似系数、dr(s)是细节系数。是尺度函数,是小波函数。
在三种类型的所有驾驶人中各随机选取一名驾驶人的速度数据进行小波分析,分别为7 号(谨慎型)、32 号(一般型),50 号(激进型)。采用db4 小波基进行4 层离散小波变换,小波系数重构后,d1-d4分别表示每层的细节系数,a4 为第五层近似系数,重构后的速度小波系数如图3 所示。

图3 重构后的速度小波系数
从图3 中可以看出,三名驾驶人的小波系数存在明显的差异,体现在不同时段下的振幅具有不同的特点。7 号驾驶人的d1 层细节系数的振幅大小在-0.05~0.05 之间,换道过程速度变化较小,符合谨慎型习性;32 号驾驶人的d1 层细节系数在0~5 s 和35~40 s 过程中变化较大,其他时段相对稳定;50 号驾驶人的d1 层细节系数的振幅大小在-0.4~0.4 之间,换道过程变化较大,符合激进型习性。为深入分析小波系数,现将各驾驶人的小波各层系数绘制为直方图以便分析,三名驾驶人的近似系数与细节系数的直方图分布也有所差异,且p为频数。7 号驾驶人呈现为三峰,32 号驾驶人为中偏双峰,50 号驾驶人为右偏双峰状态。并且各驾驶人的细节系数直方图分布也存在差异,如图4-6 所示。
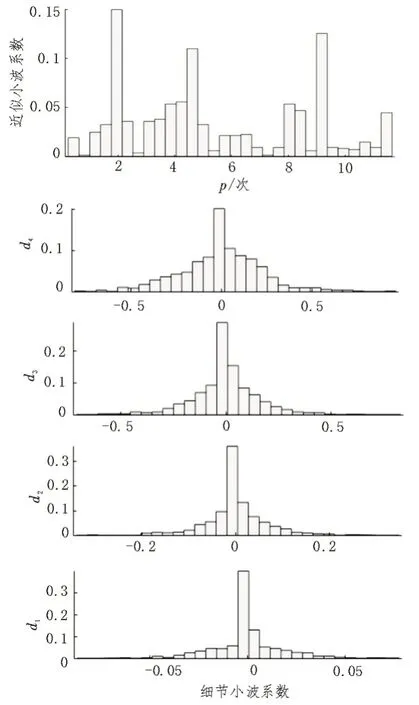
图4 7号驾驶人频域分布

图5 32号驾驶人频域分布
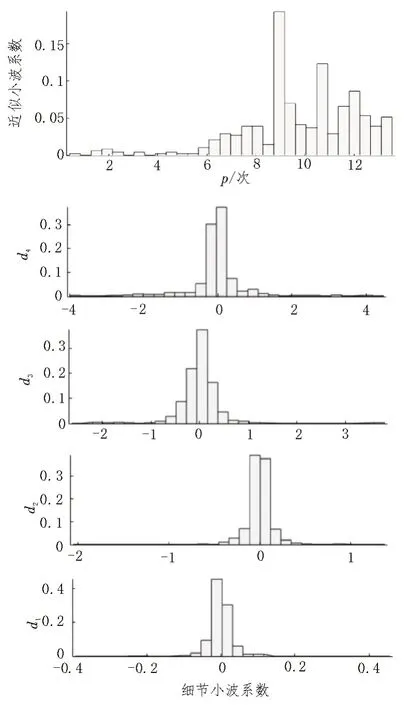
图6 50号驾驶人频域分布
3 驾驶员风格辨识模型
3.1 支持向量机
利用SVM[10-11]方法在训练集上寻找最优分类函数时,将最优函数转化为寻找超平面之间的最大分类区间问题。且分类问题可以转化为下列方程:
其中,ω为权重向量和b为偏移向量,训练样本为(xi,yi),ξi均表示松弛变量,n表示训练样本数量。参数C是可调参数,也称为惩罚系数,最后得到:
利用粒子群算法寻找最优参数C和内核参数g,得到最优SVM 模型。
3.2 粒子群算法及其改进
在PSO 算法中,该文提出以下策略对粒子的速度和新位置进行更新。
基于惯性权重非线性变化策略,可表达为:
其中,t是迭代数,T是总迭代数,K是权重因子。
基于粒子的最大速度非线性递减的方法,可表达为:
其中,Vmax与Vmin是最大速度的最大最小值。
3.3 改进PSO-SVM模型的建立与结果
改进PSO-SVM 识别模型[12-13]关键在于优化两个关键参数,训练集与测试集取7∶3。构建PSO-SVM模型的具体步骤如图7 所示。
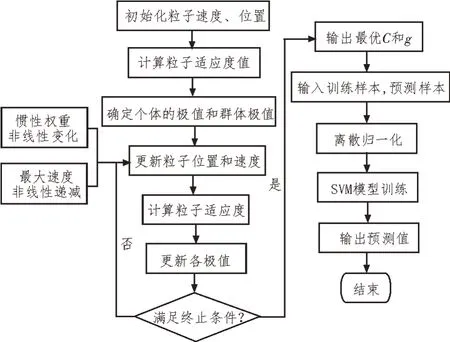
图7 算法流程
学习因子设置为c1=1.5和c2=1.7。设置粒子群优化算法的最大迭代次数为50 次。参数的最优适应度和迭代数如图8 所示。
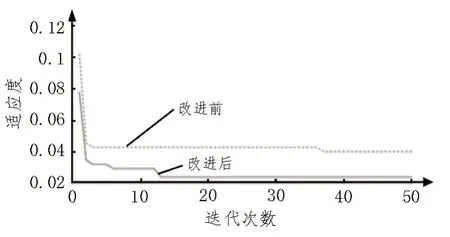
图8 迭代曲线
与PSO-SVM 相比,改进后的收敛精度和收敛性能得到了提升。最终训练得到最优参数C=81.644 8,核参数g=0.1。然后,利用测试集样本获得模型的预测精度。训练集准确率达97.580 6%,测试集准确率达96.25%,说明该模型的准确率较高,如图9 和图10 所示。
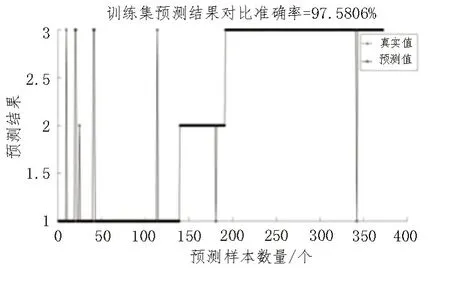
图9 训练集准确率

图10 测试集准确率
为进一步验证模型识别预测的效果,引入精确率PPV、召回率TPR 两个指标来描述该模型[14]。可以看出精确率可达94.5%,召回率可达92.83%,达到了较高的辨识预测效果,混淆矩阵如表4 所示。

表4 混淆矩阵
3.4 辨识模型的对比分析
以不同的换道参数组合作为模型输入来验证改进PSO-SVM 模型的识别准确率,并且确定驾驶风格识别模型的最优主成分组合输入,经过10 折交叉验证后进行准确率评估。与此同时,将不同参数组合输入到BP 神经网络[15]、PSO-SVM、随机森林[16]、KNN[17-18]中进行训练,来对比验证该模型的识别效果。结果如表5 所示。
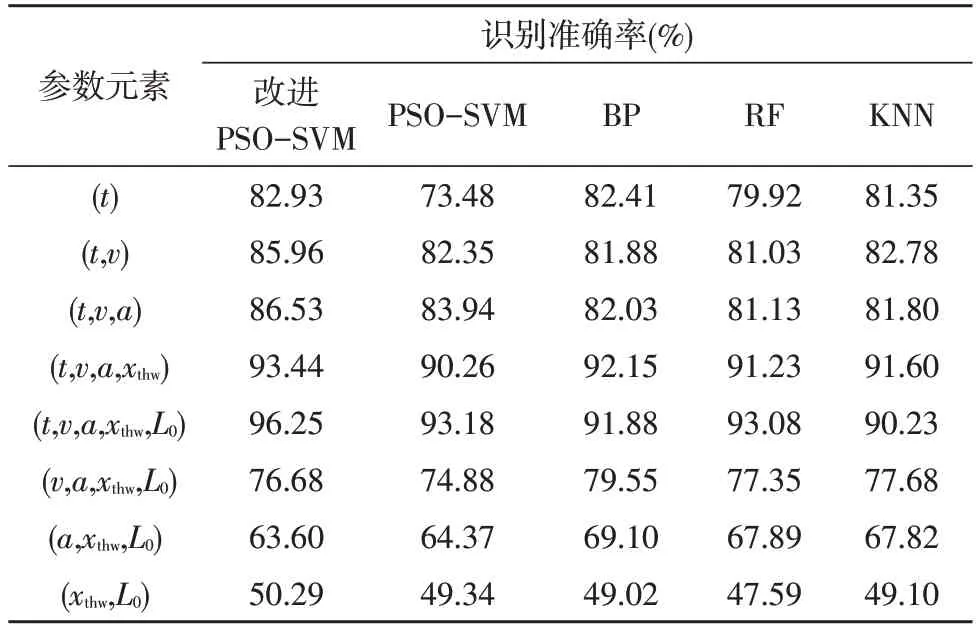
表5 各参数输入的模型识别准确率
从表5 中可见,单独选择(xthw,L0)组合或者(a,xthw,L0)组合作为模型输入,识别准确率都不佳,而加入(t,v)或者(t,v,a)组合之后模型的识别准确率明显提高。因此单一的(t)或者(t,v,a)组合并不能明显反映驾驶人的换道特性。随着(t,v)或者(t,v,a,xthw)组合的增加,模型识别准确率也随之增加。总体上粒子群优化的支持向量机和所选机器学习算法,以(t,v,a,xthw,L0)组合作为输入时,其模型效果和准确率最高。
4 结论
基于NGSIM 数据集子集US-101 路段所采集的车辆轨迹数据[19-20],通过聚类后得到谨慎型、一般型、激进型三类驾驶人。通过统计分析和时频分析可知,所提取的换道特征参数可在不同程度上表征驾驶员的换道特性,符合客观事实要求。
将不同的换道参数作为特征参数作为输入,建立基于PSO-SVM 的驾驶人风格辨识模型,精确度可达94.5%,召回率可达92.83%,并且和一些机器学习算法相比较,以(t,v,a,xthw,L0)组合作为特征参数输入的模型具有更好的辨识精度,准确率可达到96.25%。然而该文在驾驶的换道指标的采集上仍有一定的不足之处,由于数据集的限制,未考虑周围环境信息与驾驶人等特征指标。对于驾驶人辨识的敏感度还需要进行一步的分析。但是,可以说明在换道工况下借助改进PSO-SVM 模型可以识别驾驶员的风格差异,可以为驾驶人的换道风格识别以及驾驶人的非常态行为辨识的研究提供支持。

