基于CNN 与Bi-LSTM 的异常用电行为甄别算法研究

余向前，张磊，胡晓祥

（国网甘肃省电力公司张掖供电公司，甘肃张掖 734000）

随着我国电网规模的不断扩大，电能成为了重要的二次能源。由于电力的使用与生产生活密切相关，因此电网的安全、平稳运行对促进社会稳定及经济发展均具有重要意义。近年来用户窃电、欺诈用电等行为时有发生，不仅增加了电力的非技术性损耗及系统负荷，也给电网运维部门造成了一定的经济损失，还引发了诸多的社会性安全问题[1-4]。

深度学习(Deep Learning，DL)技术的发展提升了对电力用户数据隐含特征的挖掘效率，并为分析其用电行为提供了理论基础[5-7]。该文基于电力系统的数字化转型开展了对用电行为甄别技术的研究。基于用户的用电数据，结合深度学习技术建立了行为甄别模型。该模型可以有效提高窃电稽查的效率，准确判断用户的非正常用电行为，进而降低非技术性损耗给电网带来的经济损失。

1 理论设计

1.1 网络单元设计

该文采用的卷积神经网络(Convolutional Neural Networks，CNN)[8-12]是一种基于卷积运算的深度学习算法，其可提取训练数据中的原始特征。在卷积神经网络中，主要包括卷积单元与池化单元。其中卷积单元的运算如图1 所示。

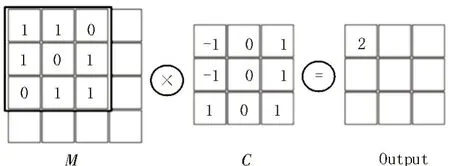
图1 卷积运算过程

图1 中，M是卷积矩阵，C为卷积核。卷积核的引入能够增强网络对于局部特征的提取能力，而卷积核的尺寸可以定义“局部”的大小。设每层卷积后获得的特征矩阵为Hi，则卷积层的输出可表示为：

式中，⊗为叉乘运算；Wi为卷积层中的卷积核权重；bi为偏置矩阵；f(·)为卷积层使用的偏置函数。该文卷积网络选择了ReLU 函数作为偏置，该函数的计算方式为：

在实际应用中，卷积层后通常紧跟一层池化层，其可对特征进行二次提取，同时减少因卷积运算而产生的参数，进而降低网络的训练代价。

最大值池化的运算过程如图2 所示。该运算在池化区域内选择最大值作为该区域的特征值。通过最大值池化，能有效降低特征维度。CNN 网络在经过多次卷积、池化计算后，通常使用全连接层来处理分离结果。

图2 池化运算过程

1.2 改进循环网络

CNN 网络虽具有较强的非线性拟合能力，但由于本次在进行电力行为甄别时主要处理的是时间序列，其无法提取该序列的时间关联特征。因此，文中引入了一种基于长短时记忆(Long Short-Term Memory，LSTM) 单元的改进循环神经网络(Recurrent Neural Network，RNN)算法。

LSTM 单元中信号的传递示意图如图3 所示。传统的RNN 网络[13-14]在提取长时间序列时，会产生梯度消失的现象。在LSTM[15-16]中，通过使用输入门it、输出门ot及遗忘门ft对信号传递进行智能控制，可以有效提升网络的训练效率。

图3 LSTM单元信号传递示意图

记w(·)、b(·)分别为每个门的传递权重与偏置量，ht为隐藏层的输出，σ为核函数，⊙为逻辑同或运算，则可得到LSTM 中各个门的信号更新方式如下：

由于用户的用电数据是与时间强相关的序列信息，因此，文中采用了双向LSTM (Bi-LSTM) 模型。该模型的结构示意图如图4 所示。

图4 双向LSTM结构示意图

对于t个时刻的用电数据，其序列化后可表征为：

Bi-LSTM 能够同时提取前后两个方向的数据特征，对于当前时刻，该模型的输出向量为：

1.3 网络过拟合方法

由于文中使用了CNN 与Bi-LSTM 相结合的网络架构，使得所提模型的整体结构相对复杂。因此为了防止网络在识别用电行为的过程中出现过拟合现象，还引入了一种基于Dropout 和自适应矩估计(Adaptive Moment Estimate，Adam)的网络防过拟合方法。

而在网络训练过程中，并非每个神经元均对网络分类起正向作用，所以对于网络中的所有计算单元，还需引入p来表示该单元被弃置的概率：

其中，pa为样本a分类结果为1 的概率；Ba为样本a所属类别样本中对于网络起负向作用的样本。使用交叉熵作为定义方式，则有：

式中，θ为训练样本经网络预测后的概率分布；θ′为训练样本的实际概率分布。

此外，在进行模型训练时，该文使用了Adam优化器。相较于传统梯度下降算法(Gradient Descent，GD)，该优化器采用损失函数梯度的一阶矩、二阶矩对参数学习率进行动态估计。在每次矫正后，学习率均处于一个确定范围内，从而保证了参数的稳定性。

在优化时，Adam 首先要计算损失函数J在t时刻的梯度：

式中，ξ为网络中的训练参数。记mt为梯度的一阶动量，vt为梯度的二阶动量，将t=0 时刻的m0置为0。此时，可以得到一阶、二阶动量的更新方式为：

式中，β1与β2分别为一阶、二阶动量的衰减系数。

在动量的更新过程中，需要及时纠正偏差对于优化初期的动量影响。将、记为纠正后的一阶、二阶动量，并引入偏差纠正方法如式（11）所示：

最终，获得网络中参数ξ的更新方法如下：

式中，α为Adam 算法的学习率，文中将其初始值设为0.001；ε为分母的外置因子，通常取ε=10-8，从而避免训练过程中分母为0 的情况。

2 测试与数值分析

2.1 实验设计

基于上述理论基础，该文使用CNN 网络提取数据中的深层特征，同时利用Bi-LSTM 网络评估用电数据的时间序列特性，进而构建了CNN-Bi-LSTM复合模型。基于该模型的用电行为甄别流程如图5所示。

图5 该文模型的用电行为甄别流程

为了验证所提算法的有效性，首先确定甄别用电行为的用户范围，并对其用电数据进行采集和标注。文中采集了某市供电公司4 237 个电力用户两个月内智能电表的三相电流数据，并基于电力大数据分析、现场稽查及专家研判的综合结果，对用户是否存在窃电的行为进行了人工标注，以获得实验所需的数据集参数。具体参数如表1 所示。

表1 算法仿真使用的数据集参数

然后根据上文所述的理论基础与数据集参数，确定CNN 网络的结构参数，具体如表2 所示。CNN在提取数据特征后，再将该特征输入至双向LSTM 网络中。此外，Bi-LSTM 网络的隐藏层单元个数为100个，CNN 和Bi-LSTM 的复合网络的输出层则为Softmax 层。

表2 CNN结构参数

根据网络结构，可得到CNN 及Bi-LSTM 网络的训练参数分别如表3-4 所示。

表3 CNN训练参数

表4 Bi-LSTM训练参数

为了合理评估该文算法的性能，文中对其进行了训练和测试实验。实验所采用的硬件平台如表5所示。

表5 算法仿真硬件平台

2.2 实验结果

算法的测试可抽象为二分类问题，即行为甄别的结果只有两类：存在窃电行为与不存在窃电行为。因此文中使用二分类问题常用的评价指标体系，即精确率(Precision)、召回率(Recall)和F1 值来对算法性能进行评估。三个指标的定义方式如下：

该文在评估所提算法(CNN-Bi-LSTM)的性能时，选择了CNN、Bi-LSTM 以及CNN-LSTM 网络作为对比算法。四种算法的训练鲁棒性以及相关测试指标对比结果如表6-7 所示。

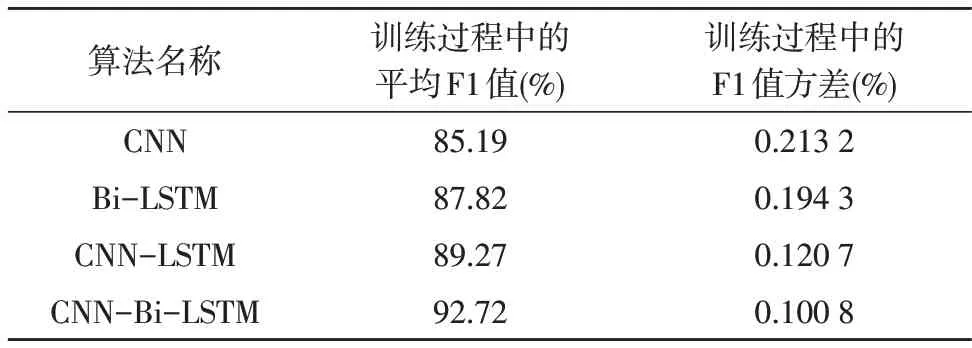
表6 不同算法的训练鲁棒性对比结果

表6 显示了不同算法的训练稳定性，由表6 可知，CNN 网络的F1 值方差为0.213 2%，该文算法则为0.100 8%，与前者相比降低了52.72%。由此说明，该文算法的鲁棒性明显提升。而从表7 中可以看出，所提算法的准确率、召回率及F1 值均有显著提升。且相较于CNN、Bi-LSTM 网络，该文算法的F1 值分别提升了10.04%和8.32%。对比表6-7 的结果可看出，该文算法在训练与测试时的F1 值较为接近，仅相差0.03%，而三种对比算法分别相差了2.48%、3.39%和0.96%。由此说明，改进后算法的泛化性能与训练结果更为接近，因此不易出现过拟合现象。

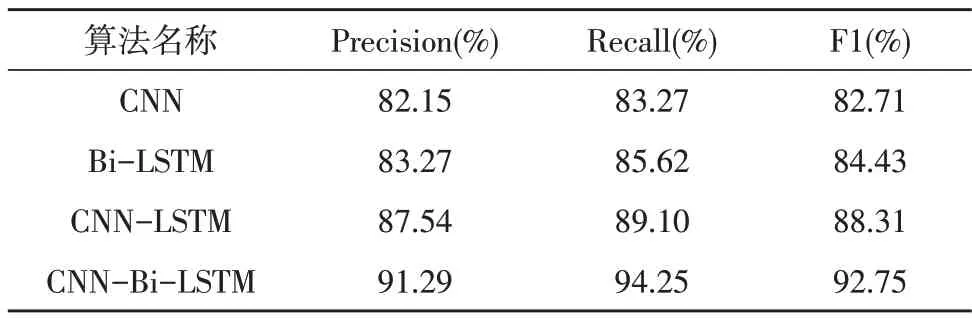
表7 不同算法的评价指标对比结果

3 结束语

该文结合CNN 及LSTM 这两个主流深度学习框架中的优势，建立了基于CNN-Bi-LSTM 的异常用电行为的甄别模型。仿真结果表明，所提算法的识别精度、鲁棒性等指标较现有算法有了显著改善。未来，随着电力系统数字化进程的加速，可将该文算法应用于各类反窃电场景中，以期为电力系统的安全、平稳运行保驾护航。