基于模型预测控制的水电站系统运行控制策略

刘旭东，黄虎军，冷国华，李夏，施兆荣

（广西桂冠电力股份有限公司（红水河）集控中心，广西南宁 530000）

随着全球变暖成为一个严重的问题，各国一直在努力减少化石燃料的使用。水力发电在绿色转型中发挥着重要作用，这是因为水力发电是唯一可以按需提供能源的可再生技术[1-2]。复杂的运行要求使模型预测控制(Model Predictive Control，MPC)成为一种有吸引力的水电运行控制方法[3]。MPC 是一种基于系统当前状态和给定信息作为初始点，通过求解有限视界开环最优控制问题(Optimal Control Problem，OCP)来计算未来控制输入序列的控制方法[4]。应用控制序列中的第一个控制输入，并在每个采样时刻重复此过程。换句话说，MPC 具有处理具有多个输入、输出和约束的动态系统的能力[5-6]。文中提出了基于模型预测控制的水电站系统运行控制策略系统模型，并制定了参考跟踪OCP，使水位保持在特定范围内。通过在储层中保留缓冲空间，该MPC 方法获得了处理系统不确定性的能力。此外，文中还对模型进行了参数更新。为了在进水预测不确定的情况下更好地运行，采用参考区域跟踪OCP 实现了多目标优化MPC。在此基础上，提出了一种能最大限度提高库区水位的新型OCP 方案，并与常规OCP 方案进行了比较。尽管新的OCP 具有不浪费水库水的优点，但在系统不确定性的情况下，其鲁棒性较弱，因此，采用多级MPC 解决这一鲁棒性问题。

虽然已经有了一系列关于MPC 用于水电站运行的研究[7-8]，但尚未进行严格的参数调整。因此，文中旨在调整MPC，使其在最小化计算需求的情况下安全、环保地运行水电系统。为了确定MPC 在严格操作下的适当调整，使用了不同的测试集和预测视界长度进行模拟。通过对仿真结果的比较，得出了合适的权值参数调整和合适的预测视界长度。

1 系统描述

1.1 系统模型

为了保证水电站有效、高效运行，水库水位的控制至关重要。将水库分为两部分，水库的上部称为M区域，下部称为D 区域，D 区域靠近大坝和工厂。流入水库的水（水速为Vi）有各种来源，如降水和融冰。其中，一定比例的水流入D 区域，其余的流入M 区域。水通过闸门（水速为Vg）和水轮机（水速为Vt）排出。

系统中有两种状态的水位，一个为M 区域的水位，另一个为D 区域的水位，分别记为h1和h2，这两种状态都是可测量和可观察的。xM和xD分别表示M区域和D 区域海平面以上的水位，其计算方式为：

系统中的两个控制输入是水库两个闸门的开启高度[9]。水闸结构如图1 所示，水闸向上打开。因此，通过D 区域水位的最小值h2或闸门的开启高度hgi来计算通过闸门的流量。防洪闸门位于水位的低调节值以上。当D 区域水位h2低于水位的低调节值时，水不从闸门流出。水闸的两个开启高度分别记为hg1和hg2。水闸的开度和D 区域水位决定了通过水闸排出的水速Vg，即:

图1 水闸结构

其中，Cd为流量系数，g为重力加速度。闸门宽度记为w，闸门最大开启高度限制为5.6 m。

发电量计划记为We，由水位、价格、需求等多种因素优化确定[10-11]。水轮机的水速Vt由发电计划所需的发电量决定，如下:

式中，xq表示放水的码头水位。a和b表示通过数据拟合方法得到的参数。码头水位由以下三次方程计算:

其中，c1、c2、c3、c4、c5为多项式数据拟合方法得到的系数。

文中使用了D 区域水电站历史存储的数据。D区域水电站下游水速Vo计算为：

1.2 操作约束

在实际生产过程中，会设定一些操作限制，用于确保操作安全，保护生态动物群，避免对水道和水电站周围财产造成破坏。主要限制因素如下：

1）下游水速Vo的突变会危及河道的性质和生态系统，因此，下游流量必须尽可能保持恒定。在每个时间步长，下游流量的变化应小于50 m3/s。

2）下游水速Vo必须大于4 m3/s，这一约束是为了保证下游的鱼类能够沿河道自由移动。

3）M 区域的水位xM必须保持在一定范围内：

式中，xLRV和xHRV分别表示水位的低、高调节值。

4）通过水轮机的最大水速Vt被限制为36 m3/s。

1.3 最佳控制问题

在水电站运行过程中，在考虑运行约束的情况下，尽量减少不必要的闸门使用，最大限度地提高水库水位[12]，否则，会导致水的损失，而这些水本来可以用来发电。因此，为了在满足运行约束的情况下实现预期的运行，将OCP 中的目标函数设为:

式中，右侧第一项旨在将M区域水位升高至HRV值，表示为：

式（8）中的第二项和第三项分别是最小化水闸开口的使用和最小化水闸开口的变化。uc表示在开环优化中通过预测视界所采取的控制动作。可以表示为(uc,t+i-1-uc,t+i-2)2。p2wp是对违反关卡约束的惩罚。变量p是由优化器自动决定的松弛变量。wR、wu、wΔu和wp是OCP 目标函数的权重参数。如果在某个权重参数上设置较高的值，则在求解OCP 时更重视具有该权重参数的项，因此，可以实现预期的操作[13]。

2 仿真设置

下面介绍在D 区域水电站运行基于模型预测控制的水电站系统运行控制策略系统模型的参数测试集和模拟条件。

2.1 参数测试集

水电站的理想运行方式是尽量减少闸门的使用，使水库的水位保持在尽可能高的水平，从而不浪费水库内的水。然而，为了安全、环保地运行，下游的流量与闸门开口的变化有关，尽可能保持恒定流量是很重要的。

考虑到最大化水位的重要性，将wR设为10，将wp设置为10 000。在所有的测试集中设定wu为1。因此，测试集上的唯一变量是wΔu。wΔu越高，越能抑制闸门开度的变化。为了显示模拟中的差异，将测试参数分别设置为1、10、100 和1 000。

在D 区域水电站实施MPC 时，通常将预测视界长度设定为13 天。文中对权重参数的每个测试集进行测试，如表1 所示，并对七种不同的预测视界长度（1,3,5,7,9,11,13）进行测试，以找到一组适合D 区域水电站严格运行的参数。

表1 测试集参数

2.2 模拟条件

为了获得真实的模拟结果，采用了历史存储的入水量和发电量计划数据。图2 所示为D 区域水电站2023年4月15日至2023年5月15日的历史发电量。

图2 历史发电量计划

入水量预报每24 小时更新一次，其包含未来13天可能流入水库的水量。采用历史数据进行模拟，选择其中一个集合运行确定性基于模型预测控制的水电站系统运行控制策略。

模拟遵循图3 框图中所示的顺序，MPC 根据给定的测量状态、入水量预测数据Vi和发电计划We信息优化最优控制序列。最优控制序列的第一个输入u*应用于具有第一个入水量预测值的系统。在此仿真中，假定模型与系统之间不存在不匹配[14]。

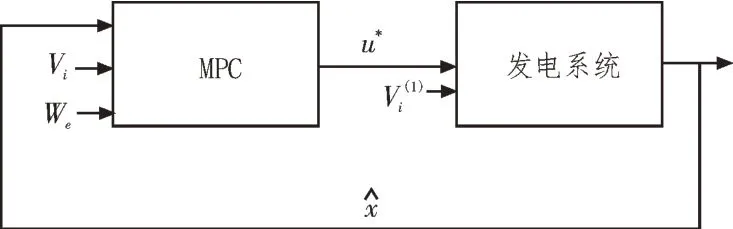
图3 MPC框图

3 仿真结果

下面研究不同权重参数测试集和预测视界长度的组合。图4 所示为在不同预测视界长度下，模拟过程中M 区域水位xM和水位界xHRV的变化情况。在图4 中，Np:i表示将预测视界的长度设置为i天。图4(a)所示为当权重参数设置为测试集1（常规设置）时，M 区域水位随预测视界长度的变化情况。图4(b)所示为设置权重参数为试验集4(wΔu=1 000)时，水位随预测层长度的变化。

图4 模拟过程中M区域水位的变化

在图4（a）中，wΔu设为1，wR设为10，其操作的目的是使水库水位最大化。除预测视界长度设置为1天（Np:1），其他数模拟结果都是根据入水量预测、发电量计划和水位需求变化的最大化水量。当预测视界长度设为1 天（Np:1）时，预测视界较短，无法充分预测水位需求变化。因此，可以观察到一个剧烈的水位下降。

在图4（b）中，wΔu设为1 000，wR设为10，其目的是使闸门开度的变化最小。因此，没有优先考虑最大限度地提高水库的水位，不同预测视界长度下的模拟结果显示出相似的水位性能[15]。而当预测视界长度设为1 天（Np:1），在最大水位需求发生变化的400 h 左右，水位明显下降。

图4 中的两幅图表明，当预测视界长度设置得较小（24 小时）时，MPC 无法经准控制系统。而当设置的预测视界长度为13 天时，整个模拟时间内的水位变化基本一致。

M 区域的平均水位、预测视界长度在不同参数测试集的模拟结果如表2 所示。当预测视界长度大于7 天时，各权重参数测试集的平均水位趋于一致，平均水位随着预测范围的缩短而偏离。

表2 整个模拟过程中水位的平均值

图5 显示了预测视界长度为3 天时，水电厂权重参数试验集的总流量Vo。随着wΔu值的增大，流量变化更为微妙。这是因为当wΔu较高时，优化器会对高值进行补偿，使闸门开口的变化最小化。设置较高的wΔu值有利于保持下游流量尽可能恒定。因此，测试集4 的下游流量变化最为平稳。

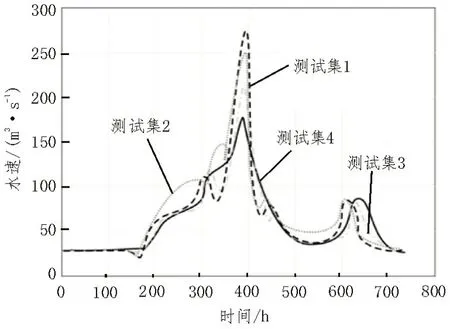
图5 当预测视界长度Np为3天时，不同参数组的下游水流流量Vo

图6 所示为每个循环的平均计算时间。随着预测视界长度的延长，计算量也随之增加。这是由于预测视界长度越短，OCP 越小。因此，将预测范围设置得更短，以预见未来并生成适当的控制序列是有益的，因为这样可以保持OCP 的大小紧凑。

图6 平均计算时间

4 结论

文中对不同权重参数和预测视界长度的模拟结果进行了对比，以找到一组合适的参数来实现水电站的严格运行。常规MPC 不仅计算效率低，而且不满足下游恒定流量的约束。当对比其他模拟结果时，无论预测视界长度如何，由于下游流量变化的操作限制，测试集1 和测试集2 均不理想。当预测视界长度为1 天(24 h)时，MPC 在水位控制方面的性能会变得很差。这是因为预测范围不够长，无法预测水位需求的变化。因此，参数的适当组合为测试集3和测试集4，且预测视界长度大于3 天。然而，预测视界长度较大时增加了计算需求。综上所述，如果预测视界长度为3 天或5 天时，可能导致OCP 更快地收敛，则使用测试集3 是正确的。如果期望下游流量的变化更平稳，则使用预测视界长度大于7 天的测试集4 是合适的。