露天爆破中炸药单耗对岩石破碎块度的数值模拟研究

黄永辉，李永杰，杨 阳，熊卫国，张智宇

1) 昆明理工大学电力工程学院，昆明 650500 2) 北京科技大学土木与资源工程学院，北京 100083 3) 香格里拉市云矿红牛矿业有限公司，迪庆 674400 4) 昆明理工大学国土资源工程学院，昆明 6500931

随着现代工业技术的高速发展、设备的更新迭代，露天爆破技术也在朝向精细化、数字化和智能化方向快速发展，爆破破碎块度作为影响二次装铲运输、破碎加工、熔炼提纯等后续工艺环节的最为重要指标之一，其影响因素包括炸药单耗、孔网参数、微差时间等，爆破破岩块度的现场统计和预测方法一直是相关领域的研究热点和痛点，该问题在数值仿真方法分析爆破破岩过程中尤为突出.

目前国内外关于爆破块度分析和预测研究主要集中在现场统计、模型试验和数值仿真三个方面，现场统计方面：洪叶荣等[1]为了提高岩石的破碎率，利用理论推导和现场试验相结合对压碴厚度进行研究，提出采用压碴爆破技术控制大块率的技术方案；刘强等[2]采用三维激光扫描仪对爆堆整体进行扫描, 建立点云模型提出爆破块度统计预测方法(3DPCFM)；骆浩浩等[3]、王韶辉[4]采用数字图像识别技术，对爆堆矿岩块度分布进行处理，计算分形维数达到优化爆破参数、降低破碎块度的目的；Strelec等[5]总结爆破岩体破碎的预测和分析，对岩石破碎块度进行预测；Kiliç等[6]、杨洋和吕文伟[7]利用标准力学试验测试岩石物理力学特性，对岩体特性与块体破碎度之间进行统计分析，明确爆破作用下块度的分布特征；杨仁树等[8]研究三种不同炸药对铁矿石破碎效果的影响，结果表明炸药的爆热越大、炸药与矿石波阻抗越匹配，矿石的破碎越充分.模型试验方面：用于研究爆破块度的方法主要是模型试验法，众多学者通过几何相似、材料相似和动力相似理论对缩比例的模型材料进行研究[9-13].李祥龙等[14]、胡涛[15]确定相似模型的单值条件及相似准则，利用爆破漏斗模型试验验证了相似准则，对台阶抛掷爆破进行研究.张智宇等[16]对在一定程度上反应原型特征的相似材料试件进行试验，自由面鼓包破裂后，岩体抛掷速度达到最大.周继国等[17]、雷振等[18]浇筑相似台阶模型并进行爆破试验，根据块度和破碎能变化规律，确定了最小抵抗线的范围.翟小鹏等[19]提出一种基于应变率变化的爆破块度预测模型,来研究露天台阶爆破岩石块度在炮孔近区的分布规律.Jug等[20]利用Kuz-Ram模型结合自己编写程序对爆破后的破碎块度进行估计，对破碎的体积进行预测.数值模拟方面：赵毅波等[21]建立二维有限元数值计算模型，对自由面数量和延迟时间对爆破破碎块度的影响进行研究，得到自由面数量越多，岩石中产生的裂纹数量越多破碎效果越好.冯春等[22]模拟从炸药起爆到岩体损伤破裂以及爆堆形成的全过程，验证了CDEM开展三维露天台阶爆破全过程模拟的可行性.范勇等[23]采用连续-非连续单元法(CDEM)模拟爆破漏斗形态和岩石破碎块度，得出破碎岩块的平均尺寸以药包质量的19/30次方减小的结论.Torbica和Lapcevic[24]构建了一种估算爆破岩石破碎度的理论模型，使估计岩石破碎时的的张力及裂缝半径成为可能.张宪堂等[25]、张阳光[26]利用ANSYS/LS-DYNA软件基于模型实验，研究延时和空孔直径对爆破破碎块度的影响，量化分析了碎块破碎程度，获得块度尺寸分布规律.王璐等[27]、唐洪祥[28]、刘启新[29]对运用SPH法的边界、变形、耦合等因素对实验结果的影响进行研究；王凯[30]使用SPH法对爆破漏斗的形成过程进行三维数值模拟的计算与模拟，研究药径埋深对爆破漏斗的影响.孙博等[31]利用SPH法对盲天井掏槽爆破进行数值模拟，研究爆破周边空孔、补偿系数对爆腔岩石损伤范围影响研究.

综上所述，数值模拟方面能够有效进行爆破破碎块度的统计分析和预测的相关成果很少，尤其是采用SPH法的更罕见，亟待提出有效解决方法.论文以露天铁矿工程爆破为背景，在缩比例模型试验的前期研究前提下，提出一种采用SPH法构建缩比例抛掷爆破模型，从爆破块度分布、累计质量通过率、评价指标和分形维数等方面开展了系统分析，获得了爆破破碎块度随单耗的变化规律.

1 力学试验及材料本构参数

1.1 模型材料力学试验

本研究依托于露天铁矿爆破工程，现场的矿岩静态力学性能参数如表1所示.根据表1中矿岩材料力学性能，从后续跟现场构建关联角度考虑，运用模型相似理论设计出符合上述条件的模拟材料（混凝土）配合比如表2所示.具体浇筑材料为山砂、瓜子石（粒径＜7 mm）、东极牌C32.5的水泥，如图1所示.运用基础力学测试设备对模型材料进行了单轴抗压、弹性模量、断裂韧度等测试，标定RHT本构模型参数来实现爆破的精准模拟.

图1 浇筑材料Fig.1 Pouring materials

表1 工程岩样力学性能参数表Table 1 Table of mechanical properties of engineering rock samples

表2 模拟材料配合比（质量比）Table 2 Simulation material coordination ratio (mass ratio)

分别浇筑3个尺寸为100 mm×100 mm×100 mm的正方体用于材料密度测试，3个尺寸为150 mm×150 mm×150 mm的正方体用于抗压强度测试，3个直径为150 mm、高度为300 mm的圆柱体用于单轴抗压强度测试，自然养护28 d，测试过程如图2所示，测试结果如表3所示.

图2 试件常规力学性能测试.(a) 抗压强度测试; (b)弹模和单轴抗压测试Fig.2 General mechanical properties testing of specimens: (a) compressive strength test; (b) elastic mold and uniaxial compression test

表3 力学性能测试结果汇总（平均值）Table 3 Summary of mechanical performance test result (average)

1.2 RHT本构材料参数

此次数值模拟所用的模型材料为RHT混凝土本构，其中密度、抗压强度、弹性模量如表3所示，以力学参数为基础，根据理论推导可以确定参数：混凝土材料密度ρ混；初始孔隙度ɑ0；单轴抗压强度ƒc；雨贡纽多项式系数A1、A2和A3；状态方程参数F0、F1、T1和T2；孔隙开始压碎时的压力pel；剪切模量G；压缩应变率指数βc；拉伸应变率指数βt.剩余RHT所需参数计算参考李洪超等[32]的研究成果，材料的部分RHT本构参数计算结果见表4.

表4 相似材料RHT模型本构计算参数Table 4 Similar material RHT constitutive model calculation

1.3 炸药本构材料参数

模拟采用使用DDNP起爆药作为炸药，模型材料为*MAT_HIGH_EXPLOSIVE_BURN高爆炸药，模型状态方程为*EOS_JWL，状态方程见公式(1)所示，炸药的密度ρ炸和爆速等本构参数见表5.

表5 DDNP炸药JWL状态方程参数Table 5 DDNP Explosives JWL equation of state parameters

其中：P为爆破峰压；V为单位体积炸药爆后的产物体积；A、B、R1、R2、ω为炸药特征参数；E为单位初始体积的内能.

2 爆破模型数值模拟

2.1 模拟方案

选择通过数值仿真软件ANSYS/LS-DYNA中SPH的方法来模拟模型试验的爆破过程，通过进行4组8个炸药单耗爆破模型试验，来研究炸药单耗对岩石破碎块度的影响规律.考虑现场爆破中的钻孔孔径、炸药类型，确定模拟中的炸药最小药径10 mm，最大药径35 mm，露天爆破参数见表6，炸药单耗设计结果见表7，最终通过数值软件进行建模计算.

表6 露天爆破参数表Table 6 Open-pit blasting parameters

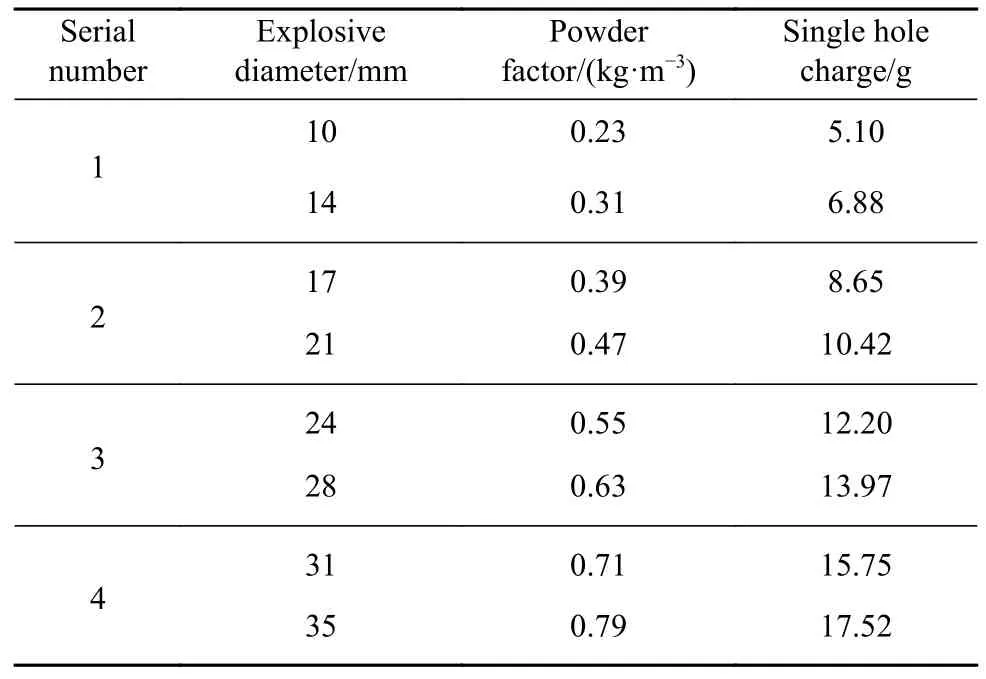
表7 炸药单耗计算成果表Table 7 Results of explosive powder factor calculations

2.2 模型尺寸

以铁矿露天爆破为研究背景，前期模型试验研究成果为依据，主要是研究新型的粒子流的块度统计方法和结果分析，为了节省成本，模型采用“背靠背”建模方式，模型试验和数值仿真模拟中均未出现相互影响现象.根据几何相似比（取值16）设计的缩比例模型尺寸如图3所示.对模型的底板台阶面设置约束，其余面均为自由边界，模拟露天矿山抛掷爆破.

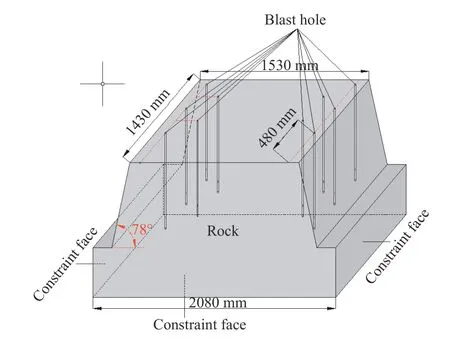
图3 数值模型Fig.3 Numerical model

2.3 模拟块度结果统计

运用LS-Prepost软件对计算结果进行处理，使用体积内能单位查看功能，根据颜色和图例可区分能量情况，给出各炸药单耗q下的模型爆破破碎情况和内能情况，如图4所示.

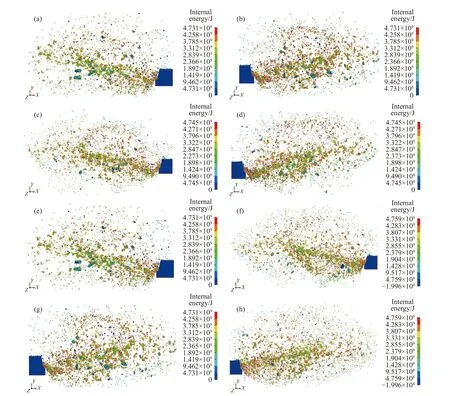
图4 块度单位体积内能情况图.(a) q=0.23 kg·m-3; (b) q=0.31 kg·m-3; (c) q=0.39 kg·m-3; (d) q=0.47 kg·m-3; (e) q=0.55 kg·m-3; (f) q=0.63 kg·m-3;(g) q=0.71 kg·m-3; (h) q=0.79 kg·m-3Fig.4 Diagram of the internal energy per unit volume of the block: (a) q = 0.23 kg·m-3; (b) q = 0.31 kg·m-3;(c) q = 0.39 kg·m-3; (d) q = 0.47 kg·m-3;(e) q = 0.55 kg·m-3; (f) q = 0.63 kg·m-3; (g) q = 0.71 kg·m-3; (h) q = 0.79 kg·m-3

根据爆堆总粒子数、粒子间距、损伤程度等判断依据，将每个块体的粒子数乘以单个粒子质量获得该块体的质量，统计计算每一个块体的体积，计算每个块体的等效长度即块度，块度小于20 mm视为完全损伤松散粒子，每隔20 mm为梯级进行划分，每个梯级的爆堆质量比总爆堆质量称为块度质量百分比，对块度数据进行排列，即可获得模拟爆破块度的分布情况，最终对应炸药单耗的块度分布如表8所示.

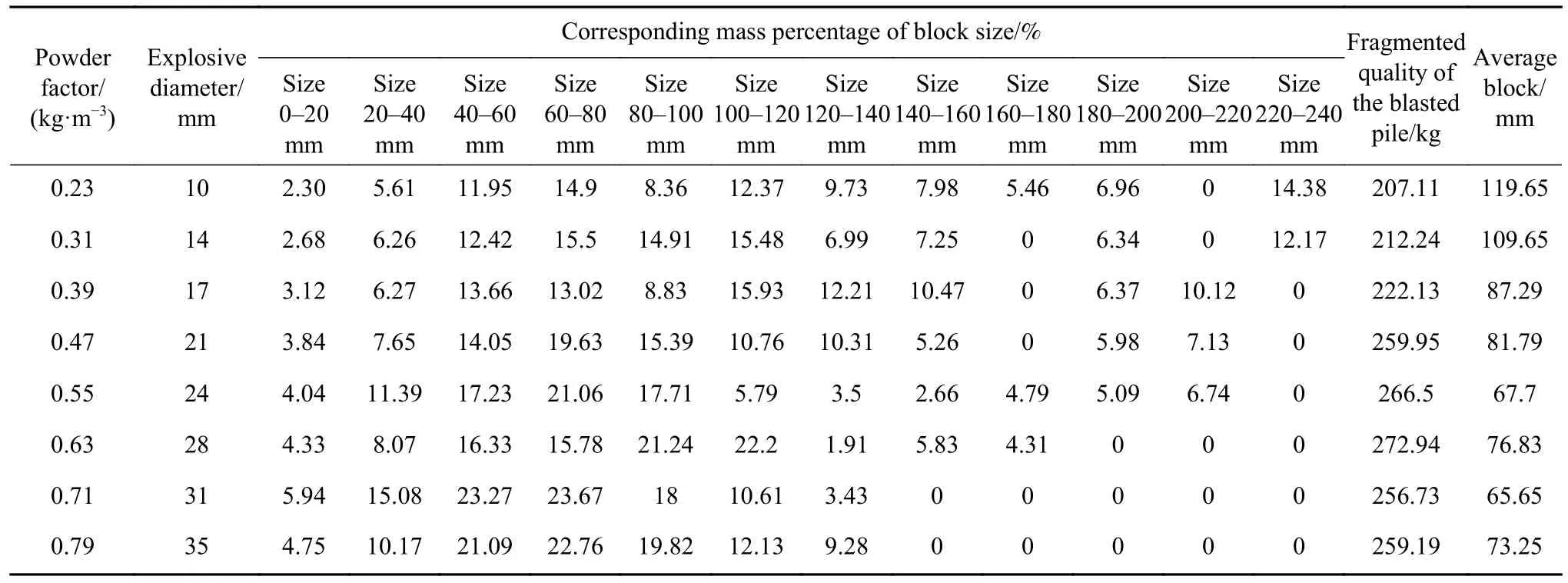
表8 对应炸药单耗的块度质量百分比统计结果表Table 8 Statistical results for the percentage of mass of blocks corresponding to the powder factor

3 爆破块度分布规律

3.1 最大块度和平均块度分布规律

炸药量影响岩块的最大尺寸与平均尺寸，炸药单耗和装药直径直接影响岩块的最大块度以及平均块度，最大块度和平均块度尺寸随炸药单耗和装药直径变化曲线见图5.

图5 最大块度和平均块度随炸药单耗分布图Fig.5 Distribution of maximum and average block sizes with powder factor

由表7和图5可得，单耗在0.23 kg·m-3～0.79 kg·m-3范围内，岩块最大尺寸dmax均小于240 mm，随着炸药单耗的增加，最大尺寸岩块总占比降低.块度最大尺寸在240、220、140 mm三个梯级分布明显，在0.23～0.31 kg·m-3、0.39～0.55 kg·m-3、0.71～0.79 kg·m-3单耗区间内最大块度尺寸变化缓慢，在0.31～0.39 kg·m-3、0.55～0.71 kg·m-3单耗区间，岩块的最大尺寸迅速减小.

岩块的平均块度davg随着炸药单耗的增加整体呈现减小趋势，炸药单耗在0.23～0.55 kg·m-3范围内，平均块度尺寸从120 mm快速减小至67.7 mm；单耗在0.55～0.79 kg·m-3范围内，平均块度尺寸上下波动，最大值和最小值分别为76.83 mm和65.65 mm.该数值模拟结果和统计得出的大尺寸分布、平均块度分布规律与实际工程现场反馈基本一致.

3.2 单耗对块度通过率的影响规律

为了定量研究炸药单耗对块度的影响，选择分形几何法，对岩块进行筛分、质量统计来体现岩石破碎程度的差异，为后续分形维数的计算提供依据.引入盖茨-高丁-舒曼（Gates-Gaudin-Schuman）分布函数（G-G-S分布），对表7中的块度数据进行拟合分析，拟合情况如图6所示，拟合得到的均匀指数n和相关系数如表9所示.G-G-S分布函数的形式为：

图6 不同单耗G-G-S函数拟合曲线Fig.6 Fitting curves with different powder factor G-G-S functions

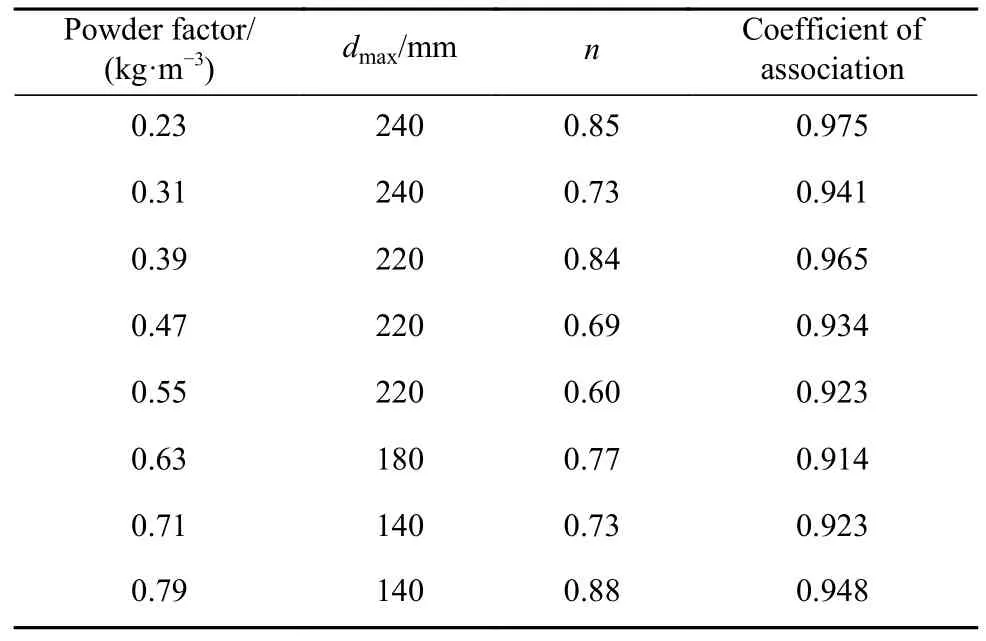
表9 爆破块度的G-G-S函数拟合结果Table 9 Fitting results for blast block size

式中：yi为等效长度（块度）小于等于代表块度的岩块累计质量比；di为各级别岩石块度；dmax为最大岩石块度；n为均匀分布参数，越小表示级配越均匀.

拟合曲线的交叉表示不同单耗通过率的变化，根据曲线交点划分区域及上述影响因素，把块度拟合曲线分为三个区III、II、I.把通过率在0.61～1.0内划分为大块度区域，在0.42～0.61内划分为中块度区域，在0～0.42划分为小块度区域.根据矿产地质勘查规范(DZ/T 0200—2020）中对于原矿石块度的规定较小，现场爆破后块度往往远大于需求尺寸，从而给中间的破碎环节产生较大成本，本着以爆代破的新理念和方法，重点研究平均块度随单耗的变化规律，以求达到资源利用最大化.

通过SPH法模拟得出的块度分布能较好的服从G-G-S分布，相关系数均大于0.9以上.从图6中可以知道，在大块区域时，通过率随着单耗的增加而递增.在中块度区域时，变化规律基本和大块区域一致，单耗为0.55 kg·m-3和单耗为0.63 kg·m-3的块度在通过率为0.56时发生交叉，在交叉点以下，出现小单耗通过率大于大单耗通过率的现象.在小块度区域，出现了拟合曲线密集相交的情况，在同一块度条件下，多处出现了小单耗超过大单耗通过率的现象.

对爆堆块度分布进行研究，利用4个常用的块度指标，最大块度、大块尺寸、平均块度尺寸和小块尺寸，分别代表：（1）爆堆中质量最大岩块的等效长度用dmax；（2）块度拟合曲线通过率为0.9时的块度用d0.9表示；（3）块度拟合曲线通过率为0.5时的块度用d0.5表示；（4）块度拟合曲线通过率为0.1时的块度用d0.1表示.提取图6中的数据，汇总出上述的4个参数，绘制成图，如图7所示.

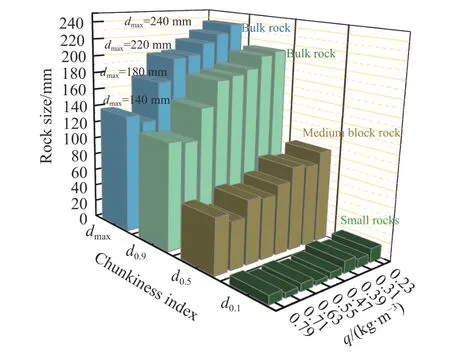
图7 块度评价指标分布情况图Fig.7 Distribution of indicators for the evaluation of block size

从图7可知，当单耗从0.55 kg·m-3升至0.71 kg·m-3时，dmax从200 mm迅速减小至130 mm，d0.9同样迅速减小.爆堆块度分布的4个常用的块度指标随着炸药单耗的增加，整体呈现波浪式降低的趋势.

3.3 单耗对分形维数的影响规律

块度分布的经验公式服从分形维数分布规律，且均匀指数n和分形维数D有以下关系：

其中，分形维数D越大，爆破破碎的裂纹发展越充分，平均块度越小.为了清晰观察炸药单耗对均匀指数和分形维数的影响规律，利用表9中的均匀指数计算分形维数并绘制图8.

图8 单耗、均匀指数和分形维数曲线图Fig.8 Uniformity index and fractal dimension curves as a function of powder factor

由图8可得，单耗从0.23 kg·m-3增加到0.79 kg·m-3的过程中，分形维数D整体呈现波浪式增加的趋势，在单耗为0.31 kg·m-3和0.55 kg·m-3出现波峰，且值分别为2.27 kg·m-3和2.4 kg·m-3；在单耗为0.39 kg·m-3和0.63 kg·m-3出现波谷，且值分别为2.16和2.23.均匀指数n的整体变化趋势与分形维数D的变化趋势相反，在单耗为0.31 kg·m-3和0.55 kg·m-3出现波谷，且值分别为0.73和0.60；在单耗为0.39 kg·m-3和0.63 kg·m-3出现波峰，且值分别为0.84和0.77.

4 结论

(1) 炸药单耗由0.23 kg·m-3增至0.79 kg·m-3的过程中，岩块最大块度均小于240 mm并呈现不同趋势的下降，主要分为三个最大块度相近和两个明显下降区，对应的最大块度尺寸梯级为240、220、140 mm；最大块度迅速下降的两个区间其对应的单耗分别为：0.31～0.39 kg·m-3、0.55～0.71 kg·m-3.

(2) 平均块度随着炸药单耗的增加整体呈现减小趋势，炸药单耗在0.23～0.55 kg·m-3范围内，平均块度尺寸从120 mm快速减小至67.7 mm，均匀指数n从0.85降至最小值0.60，分形维数D从2.15上升至最大值2.40；单耗在0.55～0.79 kg·m-3范围内，平均块度尺寸上下波动，最大值和最小值分别为76.83 mm和65.65 mm，均匀指数n先增加后减小，分形维数D先减小后增大.

(3) 爆破破岩后块度分布规律与参照实际工程现场反馈基本一致，炸药单耗的块度分布拟合曲线采用G-G-S函数拟合，相关系数均在0.91～0.97间，验证了SPH 法爆破模拟结果的岩石破碎块度统计具有可行性和准确性，从而有效克服传统模型试验成本高、试验误差等问题.