基于SIMP-安定的高速列车组合式座椅底架轻量化设计与分析

黄昌雄，陈 耕，黄松华，张乐乐

1) 北京交通大学机械与电子控制工程学院，北京 100044 2) 北京交通大学轨道车辆运用工程国家国际科技合作基地，北京 100044 3) 西交利物浦大学智能工程学院，苏州 215123

高速列车座椅底架轻量化设计不仅要满足座椅的实际承载要求，同时还需保证在列车长期服役中的交变载荷作用下不会发生显著的变形.传统座椅结构设计大多是基于现有构型进行尺寸优化，受限于构型本身的约束，无法充分发挥结构的承载潜能，同时并未考虑交变载荷引起的失效[1-3].虽然拓扑优化技术已相当成熟，且作为传统设计方法可以不受限于现有构型[4]，但其普遍以静力载荷条件下的结构刚度或局部应力水平为目标，无法得到交变载荷作用下效率最高的结构构型.因此，如何同时兼顾这两个设计需求成为列车座椅轻量化设计的关键.

不同于采用高强度的轻质新材料设计 (如碳纤维复合材料[5])，拓扑优化是指在给定边界条件、满足某种约束下寻求材料在设计域内达到某种目标的最优分布.早期发展的拓扑优化方法主要包括均质化方法、变密度法、双向渐进结构优化法、水平集方法以及相位场拓扑优化法.拓扑优化的均质化方法最初由Bendsøe和Kikuchi[6]在1988年提出，自此拓扑优化成为结构优化设计中重要的一个分支.在变密度法领域，Bendsøe和Sigmund[7]最早基于均质化原理进一步开发了基于固体各向同性惩罚微结构插值模型 (SIMP)；而Stolpe和Svanberg[8]提出的材料属性有理近似模型 (RAMP)作为变密度法另一个重要的分支，能够在零密度条件下得到非零灵敏度，并被证实可用于解决低密度值问题中的数值困难.不同于变密度法的优化准则 (OC准则)，基于启发式算法的渐进结构优化方法 (ESO) 仅能够在初始设计域较为理想的前提下获得高质量构型，为此双向渐进结构优化方法[9](BESO) 将高灵敏度的“空单元”重新恢复，对低灵敏度的“实单元”进行消除，并以此实现了对ESO算法的改进.最初用于捕捉线弹性结构自由边界的水平集方法[10]，被Osher和Sethian[11]用于开展对物理中移动界面“水平集”问题的研究，其最大优势是所得到的设计可直接用于制造，但也存在如高维水平集方程难于获得、进入非线性领域后灵敏度难以求解等困难.此外，“相位场”方法由Bourdin和Chambolle[12]首次提出，Wang和Zhou[13]的研究进一步将其扩展至固体双相/三相材料问题；由于这一优化方法同样采用了体积约束而并非严格意义上的“相位场”，因此“相位场”拓扑优化方法与SIMP法之间存在密切关联.在这些常用方法之外，近十几年来出现的新型拓扑优化方法还主要有Kobayashi[14]提出的基于细胞分裂理论的仿生布局拓扑优化法，以及Luo和Bao等[15]提出的基于材料场拓扑算法.前者由遗传算法驱动、能够以相对较少的设计变量生成一组多样化的设计.后者采用材料场级数展开技术将结构拓扑在特征映射空间进行降维表征，能够大幅度减少设计变量.在上述算法中，SIMP算法相较于其他算法，在灵敏度计算相对简易的同时还具有良好的收敛性而被广泛采用.SIMP算法最具代表性的应用之一[16]是空客A380机翼结构的轻量化设计，通过该方法设计的前缘肋板在满足了所有机械性能的同时重量显著减少.此外，在航天领域Orme等[17]也基于SIMP法以第一频率和应力水平作为设计约束，对以色列月球着陆器计划 (GLPX) 的登月飞船发动机支架质量进行了优化.拓扑优化在工程中获得了广泛的应用，即使在对结构承载安全要求极为严苛的航空航天领域，结构轻量化设计同样可以通过拓扑优化来实现[18-19].

目前的强度拓扑优化方法多以结构的应力水平不导致屈服为依据[20]，即局限于弹性设计.但大量的工程实践[21-23]表明针对承受交变载荷作用的结构，其在弹性极限之上仍存在较大的载荷裕度.基于局部应力水平的优化因未能充分利用结构的后屈服强度而无法有效实现结构减重.对结构承受交变载荷能力进行解析的常用方法之一是直接法 (DM) 安定分析[24-26]，该方法的优势主要有两点：一是具有整体性，突破了对局部应力必须小于屈服强度的苛刻要求；二是具有路径无关性[27]，可以不通过增量有限元迭代计算直接获得结构的载荷域.在诸多工程领域中，安定理论和在其基础上提出的直接法均得到了广泛应用.例如，在压力容器领域[28]，安定理论常被用于结构安全规范的制订，现已成为多个国家设计规范中的重要判据[29-31].在铁路轨道领域，安定理论也逐渐开始受到关注，并被用于研究材料的性能和厚度对多个载荷作用下无砟轨道强度的影响[32-33].

数值方法是安定理论实现工程应用的重要条件，近年来关于安定问题的求解算法也出现了诸多研究进展.如Chen和Ponter[34]、以及Chen和Chen[35]基于弹性补偿法开发了更具普适性的线性匹配算法 (LMM)；Spiliopoulos和Panagiotou[36-37]应用傅里叶级数开发了残余应力分解法 (RSDM)；Peng等[38]提出了一种通过多次求解弹性问题获得自平衡残余应力场的应力补偿法 (SCM)，等等.此外，Qin等[39]运用均匀化理论，将安定性理论进一步扩展至复合材料领域.

将安定分析与参数、拓扑等优化算法结合，实现以安定强度为目标的结构优化是近年来的研究重点[40-43]，但相关的数值问题致使安定优化在工程实际结构的应用普遍存在困难.为此，Huang[44]提出了一种安定性参数优化数值法，即以安定极限来衡量结构强度，并充分利用遗传算法的并行计算能力[45]，为密封舱结构少数关键设计参数的确定提供新方案；Chen等[46]又将安定分析方法成功应用于航天器密封舱舱体的大型可重复使用结构设计评估，研究表明所设计结构的安定强度为弹性极限的近两倍，并通过水压实验验证了其设计的正确性.

针对传统设计方法受限于已有构型约束以及未考虑交变载荷作用的不足，围绕高速列车座椅底架轻量化设计需求，依据TB/T 3263—2011[47]标准，对某型组合式座椅底架主结构进行了以刚度为目标的SIMP拓扑优化，并采用前序研究[44]中提出的方法以结构承受交变载荷作用时的强度为目标对关键部件进行了安定参数优化，通过将二者相结合形成了轻量化底架的完整设计方案.

1 面向刚度与强度的优化设计方法

1.1 基于最小柔度的SIMP法

由于具有较高的迭代效率，SIMP方法在连续体拓扑优化中受到广泛关注.在对拓扑优化设计域进行有限元网格离散后，基于最小柔度的SIMP法关于目标函数 (最小应变能) 和约束条件 (体积约束) 的拓扑优化问题构造如式 (1) 所示，问题求解需要找到满足优化条件的单元相对密度场.值得注意的是，SIMP方法对于中间灰度单元的材料属性由均质实体插值而得，如式 (2) 所示.

式 (1) 中，f(x)表示优化问题的目标方程 (即最小化结构的应变能)，x表示结构的单元相对密度场，e表示单元编号，xe表示单元e的相对密度，xmin表示单元相对密度的最小值；U、F和K分别代表总位移、力载荷和总体刚度矩阵，ue和ke分别代表单元位移矢量和单元刚度矩阵，V0和V(x)分别代表结构初始时刻的体积和优化过程中的体积，以及参数N、c和p分别代表单元数量、体积分数和惩罚因子.Bendsøe和Sigmund[7]证明当p≥ 3时插值模型时数值效率较高，因此文中采用参数p= 3.同时，限制单元最小值密度xmin为0.001，以避免数值问题.

式 (2)中，E0为均质实体单元的弹性模量；E为单元e的插值弹性模量.

如图1所示，基于最小柔度的SIMP法在计算灵敏度之后，对灵敏度进行修正，以避免棋盘格问题和使算法具有网格无关性.算法在确定灵敏度之后，采用OC优化准则对设计变量进行更新，在结构单元相对密度场xnew与前一步迭代结果xold之间的最大误差小于或等于给定容差值 (tol) 时，算法终止.

图1 SIMP算法流程Fig.1 Flowchart for the solid isotropic microstructure with penalization algorithm

1.2 基于结构安定性参数优化

为结构优化开发的安定性参数优化数值算法由内外嵌套循环组成，其中内循环采用内点法计算结构设计参数给定时的安定载荷因子，而外循环基于遗传算法寻找在满足约束条件时使安定载荷因子达到最大值的设计参数.

基于Melan下限定理[27]进行安定问题的构造.根据该定理，一旦结构经有限元方法离散后，其安定极限必须满足如优化问题 (3) 所示的条件.对该优化问题的求解，本质是寻找与时间无关的自平衡残余应力场和最大安定载荷因子α，使得经α放大后的弹性应力场在与叠加后处处满足屈服条件.

式 (3) 中，i为高斯点编号，Ci为高斯点i的残余应力场自平衡矩阵，σEik为弹性外载荷产生的弹性应力场，σYi为屈服强度，以及F(·) 为von Mises屈服函数；NG、NV分别代表有限元模型中的高斯点总数和载荷空间的载荷角点个数.

由 (3) 得到的安定极限标志着结构承受交变载荷的强度.因此，在前期研究[44]中提出了将设计参数向量γ作为变量，用于构造以表征结构承受交变载荷作用的安定强度为目标的参数优化算法.将设计对象视为以γ表征的集合B={B1,B2, ···,Bn}，则该参数优化问题如式(4)所示.

式 (4) 中，γmax和γmin分别代表设计参数向量γ的上下限；αB表示含参数的安定载荷因子.该优化问题的本质是寻找使安定载荷取最大值的参数组合.由于目标函数和自变量之间存在的高度非线性关系，为了避免传统的梯度算法易导致求解陷入局部最优的缺点，将该问题重新进行构造并基于遗传算法进行求解，其计算流程如图2所示.

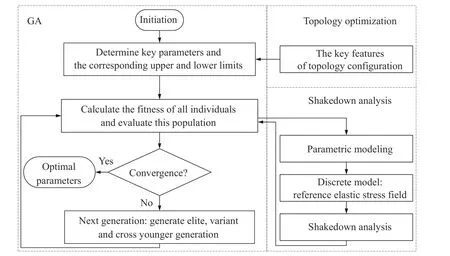
图2 安定参数优化流程Fig.2 Flowchart for the shakedown-based parameter optimization

2 座椅底架优化设计

在满足承载要求的前提下，拓扑优化技术能够在对复杂结构进行优化时节省大量设计材料.然而，在结构本身存在交变载荷作用时，传统的设计方法通常更注重局部薄弱位置的强度状态，用最薄弱位置的局部强度来代表整体结构的承载能力，这往往无法满足轻量化和可靠性的共同要求.相比之下，安定参数优化则能够充分发挥安定分析不允许结构发生持续塑形变形的特点，利用整体结构强度评估承载性能的优势，这对于作用载荷复杂的结构连接件优化显得格外的重要.

考虑到安定参数优化对大型复杂结构的多参数优化存在数值困难，座椅底架优化设计中考虑主体结构拓扑优化设计与关键部件安定参数优化设计相结合，以达到在满足承载性能前提下轻量化的设计需求.

2.1 现有座椅底架模型

高速列车座椅底架是连接座椅和车体的主要承载结构，其优化设计需要在减少结构材料的同时满足结构刚度和强度的需求.首先以结构刚度为目标对底架主结构进行拓扑优化和再设计，确保底架整体具有足够的刚度性能.其中，座椅模型依托于中车青岛四方某型列车现有座椅结构，其几何模型和相应的载荷条件如图3所示.座椅模型的下半部分为座椅底架模型，其长宽高尺寸为972 mm×346 mm×226 mm，总质量约为14.72 kg，如图3(b) 所示.

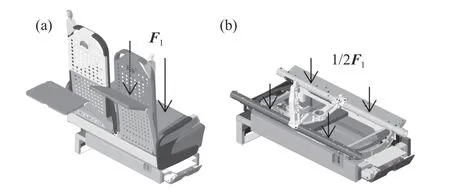
图3 某型列车座椅模型.(a) 座椅载荷; (b) 底架载荷Fig.3 Train seat model: (a) loaded on seat model; (b) loaded on seat bracket

依据座椅设计规范TB/T 3263—2011，高速列车座椅坐垫强度设计需要满足：在集中载荷F1(方向为垂直向下、大小为980 N) 的作用下，结构不出现裂痕及永久变形等缺陷并保持一定的刚度(图3(a)).将该标准规定的载荷工况转换至座椅底架结构中，确定均布载荷P1大小为0.15 MPa(图4(a)).如图4(b) 所示，进一步通过对整个底架解析计算得到L型连接件上的均布载荷P2大小为0.06 MPa.底架材料为碳钢DP590，材料模型为理想弹塑性模型，相关参数如表1所示.

表1 碳钢DP590材料参数Table 1 Material parameters of carbon steel DP590

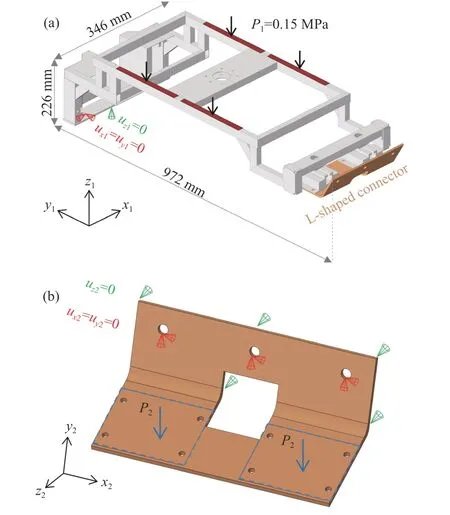
图4 现有座椅底架几何模型.(a) 座椅底架简化模型; (b) L型连接件Fig.4 Geometric model of the current seat bracket: (a) simplified seat bracket; (b) L-shaped connector

对座椅底架与车体连接边界的有限元模型进行简化: (1) 如图4(a) 所示，在全局坐标系下，对底架与底板接触面节点的位移分量uz1、螺栓孔圆周节点的位移分量ux1、uy1进行约束；(2) 如图4(b) 所示，在L型连接件局部坐标系下，对底架与侧墙接触面节点的位移分量uz2、螺栓孔圆周节点的位移分量ux2、uy2进行约束.

2.2 基于SIMP的主结构拓扑优化设计

基于现有座椅底架结构的几何形式及边界条件对称性的特征，以底架几何模型的最大外轮廓为基准，建立拓扑优化设计域1/2有限元模型，采用八节点六面体线性缩减积分单元，模型如图5所示.

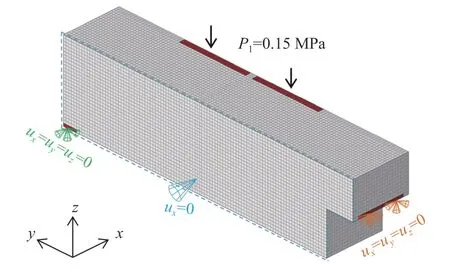
图5 拓扑优化设计域Fig.5 Design domain of topology optimization

为得到有效传力路径最优的承载结构，基于现有座椅底架的最大外轮廓建立了与设计域相对应的有限元模型.由于以设计域体积2%作为约束条件时需要大量迭代计算而SIMP算法具有迭代效率高的优势，因此选用该方法对主结构进行以柔度最小化为目标的拓扑优化.优化的目标函数及约束条件表述如式 (5) 所示.

如图6(a) 所示，主结构刚度及体积在优化进行5个迭代步后缓慢收敛，并在37步迭代停止时同时满足约束与最优条件.

图6 主结构拓扑优化.(a) 拓扑优化历程; (b)相对密度分布Fig.6 Topology optimization configuration of the main structure:(a) History of topology optimization; (b) Elemental density distribution

主结构拓扑优化收敛结果模型的相对密度分布如图6(b) 所示，结果表明：存在xe∈[0.001,1)的灰度单元；同时，在半径R为690 mm的圆弧周围分布的实单元(xe=1)占比最大.为此，将{xe=1}定义为主传力路径，并基于该路径进行几何重构设计.再设计后的构型如图7所示，与图4(a) 中现有底架主结构相比质量减小了17%.

图7 主结构几何重构Fig.7 Reconfiguration model of the main structure

2.3 L型连接件的安定参数优化

在确保座椅底架主结构刚度设计的前提下，以表征结构交变载荷下的安定强度作为依据针对座椅底架关键部件L型连接件展开参数优化，以实现结构轻量化设计并保证其关键区域的承载安全.

首先采用四节点四面体线性积分单元 (C3D4)对现有L型连接件进行建模分析，其应力及位移分布如图8所示.结构弯角处出现应力集中，位移最大发生在L型连接件下部结构的边缘.此外，L型连接件与车体侧墙作用的上部结构的应力和位移均较小，存在较大的优化裕度，因此选取该区域进行参数优化.

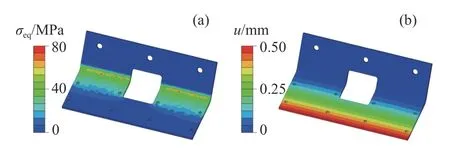
图8 L型连接件应力及位移分布.(a) 应力分布；(b) 位移分布Fig.8 Stress and displacement distribution of the L-shaped connector:(a) von Mises stress distribution; (b) displacement distribution

为此，以设计参数a和b驱动参数A、M和Q(如表2，表中的常数是与结构相关的尺寸参数)，对L型连接件进行参数化建模 (图9(a)).以该模型为基础构造安定性双参数优化问题，进而基于遗传算法采用Matlab-Abaqus联合仿真策略求解此问题.如图9(b) 所示，考虑交变载荷的角点NV=2 (即载荷域为[0,P2]).如图10所示，以a、b为7.5 mm(a、b∈[0,15] mm) 作为搜索起点进行安定双参数优化.

表2 L型连接件优化参数Table 2 Some optimization parameters of the L-shaped connector

图9 L型连接件几何和载荷条件.(a) 参数化建模; (b) 交变载荷和载荷域Fig.9 Geometry and loads of the L-shaped connector: (a) parametric model; (b) cycled loads and load domain

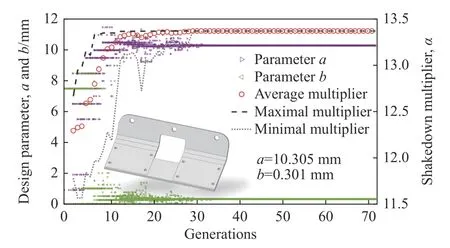
图10 L型连接件参数优化Fig.10 Optimization process of L-connector parameters

可以发现随着算法迭代，离散的样本逐渐收敛至最优解.为对该过程进行深入分析，以设计参数a、b为输入绘制了L型连接件的安定响应面.如图11所示，该响应面呈现高度非线性，因此进一步证实了选用遗传算法进行参数优化的合理性和必要性.在响应面上可以观察到样本群的收敛过程，且迭代最终得到的结构安定载荷因子α为13.40.

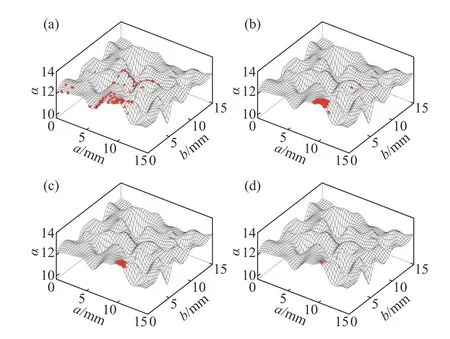
图11 L型连接件安定响应面.(a) 第10代; (b) 第20代; (c) 第40代;(d) 第72代Fig.11 Shakedown response surface of the L-shaped connector: (a) 10th generation; (b) 20th generation; (c) 40th generation; (d) 72th generation

为了进一步证明结构安定性参数优化算法的有效性，采用如图12(a) 所示的加载路径，基于增量有限元法对优化后的L型连接件进行安定承载模拟验证.图12(b) 表明在幅值PSD为0.804 MPa的安定载荷作用下，塑性耗散功导数p˙逐渐收敛至零；第二个载荷周期开始不再有新的塑性变形发生，即塑性耗散功p维持不变.因此，增量法模拟证实L型连接件在PSD作用下发生安定行为.

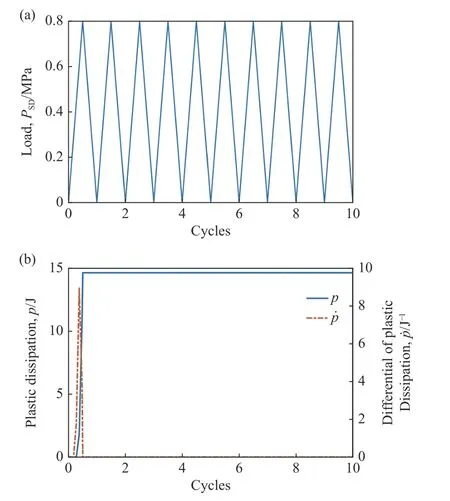
图12 优化设计结构循环加载.(a) 加载路径; (b) 塑性耗散功Fig.12 Cyclic loading of the optimization configuration: (a) evolution of cycle loading and unloading; (b) plastic dissipation

表3详细对比了L型连接件优化前后承载性能.与优化前相比，优化后的L型连接件在结构质量减小12.5%的前提下，安定承载极限和结构效率分别提高了7.8%和23%.这表明，以结构安定强度为目标的参数优化算法能够有效地提高L型连接件的承载性能，同时减轻结构重量.

表3 L型连接件优化前后的承载性能Table 3 Bearing capacity of the L-shaped connector before and after optimization

3 优化设计结果与讨论

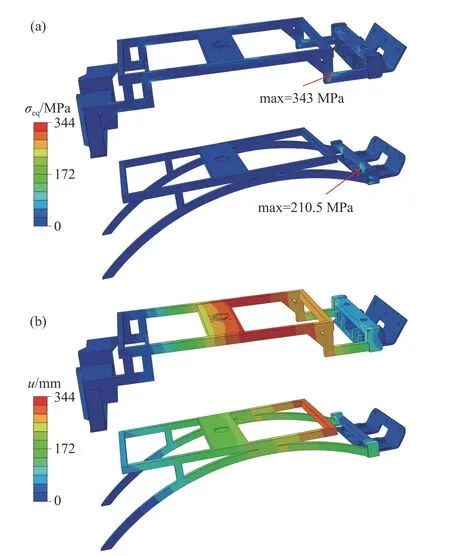
图13 座椅底架应力、位移分布对比.(a)应力分布; (b)位移分布
Fig.13 Comparison of the stress and displacement distributions of the seat bracket: (a) von Mises stress distribution; (b) displacement distribution

将优化设计后的底架主结构与L型连接件进行组合，对其整体性能进行研究.在有限元仿真计算结果中提取二者间的接触力P*2，其大小为2.4P2，并未超出L型连接件的安定承载极限13.4P2，证明了结构安定性参数优化算法对L型连接件进行优化设计的可行性.

优化前后座椅底架应力、位移分布结果如图13所示，以结构刚度和安定强度为目标的座椅底架优化设计，整体相比于现有座椅底架结构重量减少17% (表4).同时，在最大等效位移不增加的前提下，优化后构型中的关键应力水平得到了一定程度的降低，从而提高了结构的承载性能.

表4 座椅底架优化前后Table 4 Some parameters of the original and optimized structures

列车车体设计通常采用模态分析对结构进行评价.座椅底架采用机械连接方式安装到车体上，其作用主要有两个：一是作为乘客在旅途中休息的场所；二是起到加强车体刚度的作用.为了评价座椅底架的模态指标，可以采用模态分析的固有频率，特别是一阶固有频率.为此，对优化前后的底架结构进行了模态分析，相应的模态频率详细对比如表5所示.

表5 座椅底架优化前后模态频率Table 5 Modal frequencies of the original and optimized structuresHz

由于减少了材料，优化设计的底架一阶固有频率降至67.4 Hz，但其随后的5阶模态频率，相比于现有座椅底架提升6% ～ 23%.虽然优化设计的底架一阶固有频率不可避免地出现了下降，但其仍满足车体一阶固有频率高于15 Hz的设计要求，同样起到加强车体刚度的作用.而且，从图14所示的Ⅰ阶振形来看，相比于现有座椅底架，优化设计的底架位移分布更为均匀.这表明优化设计的底架可以更好地传导结构受力，承载性能更优.

4 结论

(1) 针对高速列车座椅底架传统轻量化设计方法的局限，提出了一种基于SIMP-安定的设计与分析方法，即对座椅底架主结构进行以结构刚度为目标的拓扑优化设计，同时为了避免结构轻量化导致的强度下降问题，对关键部件L型连接件进行安定性参数优化的设计方法.

(2) 在满足TB/T 3263—2011行业设计要求的基础上，高速列车组合式座椅底架优化设计实现主结构减重17%，同时使L型连接件承载交变载荷的结构效率提高23%，为同类结构优化设计提供参考.

(3) 为避免实际数值困难，综合运用整体拓扑优化设计和局部安定参数优化的方法，能够实现复杂工程结构的轻量化设计，同时保持整体结构的良好承载性能.