电火花加工用磁悬浮驱动器控制系统

赵芳　张健　孙凤　徐方超　栾博然　刘洋　张晓友

摘要：针对传统电火花加工时，主轴不能及时调整极间间隙导致加工效率低下的问题，提出了一种多自由度磁悬浮驱动器代替传统电火花主轴运动。分析了该磁悬浮驱动器的结构及原理并建立了磁悬浮驱动器的动力学模型，运用有限元仿真软件对该驱动器所产生的电磁力进行仿真分析，通过设计传统PID控制系统及模糊PID控制系统对磁悬浮驱动器的控制效果进行仿真与实验验证。结果表明，该磁悬浮驱动器具有较好的跟随特性和快速的响应速度及符合要求的电磁力，满足微细电火花加工要求。

关键词：电火花加工；磁悬浮驱动器；动力学模型；电磁力；模糊PID控制；有限元仿真；响应速度；跟随特性

中图分类号：TG661 文献标志码：A 文章编号：1000-1646（2024）01-0082-09

微细电火花加工是一种非接触电热加工工艺，对某些金属的加工具备若干优点。微细电火花加工技术不仅可以加工特殊和复杂形状的零件，而且在加工过程中无任何宏观切削力，但在传统电火花加工机床上调整工件和电极之间的极间间隙多数采用电机与滚珠丝杠配合而成，受其自身条件影响，在加工过程中难以避免地产生时间滞后、效率低下等问题。对此国内外学者就提高电火花加工效率方面做出了一定的研究。电火花加工效率提升的主要方法包括：电火花放电频率的增加，针对控制器的使用以及机械结构的改进，还有一部分学者通过改进加工方法来提升电火花加工效率。刘广民等通过减小电火花加工极间放电脉冲、增大放电间隙探索了一种基于电路共振原理的频率在30-300MHz的脉冲电源，通过改进电源放电频次达到提高加工效率的目的。胡波等建立了一种基于极间阻抗特性的微细电火花放电状态检测系统，该系统建立在极间阻抗变化特性的基础上，利用单片机芯片设计检测系统，使用串口与电源控制模块通信，实时检测极间放电状态并进行反馈，经过测试后，通过建立电火花放電状态检测控制系统达到了提高加工效率的目的。FENG等提出了一种具有高响应频率特性的磁悬浮主轴系统替代原有的机械连接结构，通过在高温合金上进行钻孔加工实验，与传统加工方式相比，其放电百分比增加30%，进一步提升了加工效率。ZHANG提出了一种在复合能量场下利用旋转短弧进行高速电火花加工的新方法。通过洛伦兹力、电场力以及工具电极的高速旋转间共同作用，在电极与工件间产生旋转的短电弧，以此提升了材料去除率和加工效率。SINGH等验证了磁场和超声振动对加工区的联合作用，使半圆形微特征的材料去除率更高，锥度更小，提升了加工效率。XU等提出了雾化放电加工法，使用氩气和氧气雾化介质进行比较实验，验证了雾化电火花烧蚀加工效率是传统电火花加工效率的8倍。NI等研发了一种结合电极振动、旋转、泵冲洗三种方式的混合旋转超声电火花加工系统，实现了更稳定的材料去除率。磁悬浮驱动器作为一种将电磁力转化为机械力的典型机电系统，具有无机械磨损、无需定期润滑、减小使用空间等优点，被应用在精密加工、密闭阀体、航空航天等领域。磁悬浮技术是利用悬浮磁力使物体处于一个无摩擦、无接触悬浮的平衡状态，通常可控的电磁力不可取代，电磁悬浮是目前市场上应用最广的一种磁力悬浮方式。

综上所述，学者们为了提升电火花加工效率，基本都是在改变机械结构或者设计不同的控制器等某一方面来提升电火花加工效率，本文提出了一种多自由度磁悬浮驱动器结构，在此基础上运用PID和模糊PID控制器设计了磁悬浮驱动器的控制系统，对磁悬浮驱动器进行仿真和实验研究，分析在不同控制策略下的控制效果。

1 多自由度磁悬浮驱动器装置

1.1 磁悬浮驱动器工作原理

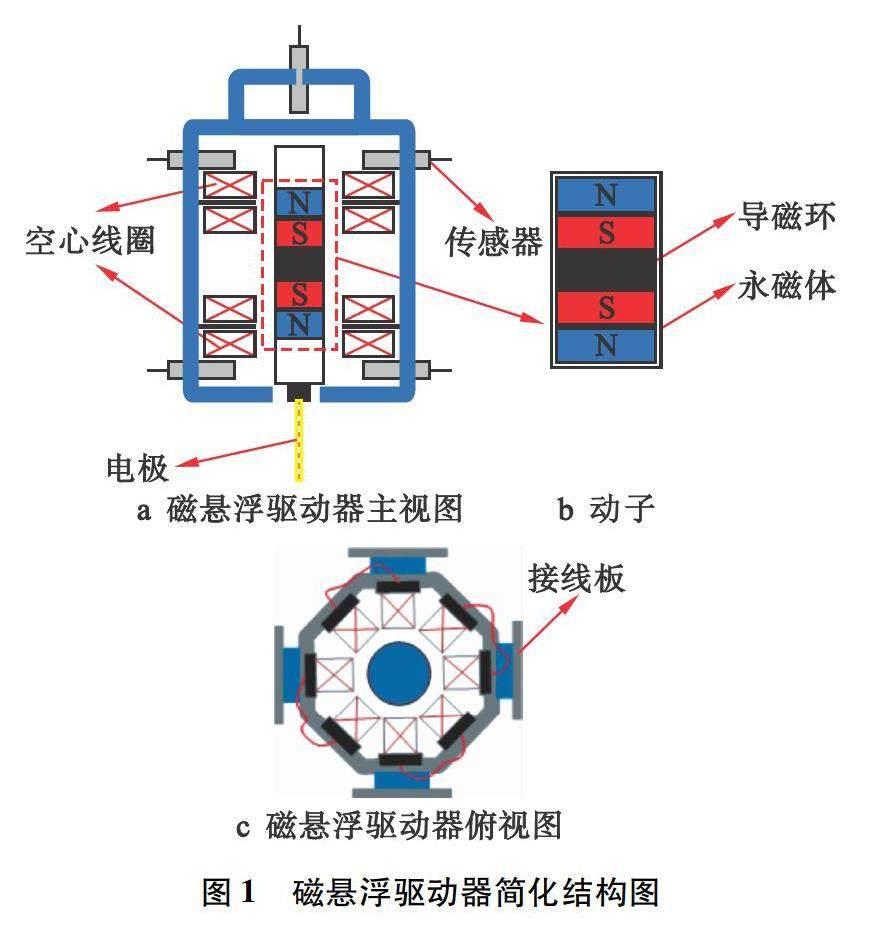
图1为多自由度磁悬浮驱动器简化结构模型。该多自由度磁悬浮驱动器主要由空心线圈、动子、位移传感器组成，其中动子由永磁体和导磁环组成，空心线圈分为上下两组，每组由8个线圈组成，5个位移传感器分别负责检测动子x、y两个方向的位移以及z方向位移。

根据电磁感应原理，向线圈中分别通人正负电流可以调节空心线圈的N/S极。在实际控制中采用dSPACE的8个D/A输出口分别控制两组线圈，进而达到控制动子多自由度运动的目的。磁悬浮驱动器动子位移变化被高精度位移传感器检测并输入到控制系统中，在磁悬浮驱动器位移控制系统中与输入的期望位移作比较，经比较后将输出的位移信号转化为电压信号，再经过功率放大器输出到磁悬浮驱动器中进行位移调节。图2为磁悬浮驱动器z方向移动原理图。

当线圈与动子间距一定时，随着电流的增加，电磁力呈现逐渐增大的趋势，电流为1A时，轴向电磁力为4N，径向电磁力略高于轴向电磁力。当线圈通入电流大小一定时，随着动子的平移，电磁力呈现上下波动的趋势，当动子沿径向、轴向移动时，0-2mm位移范围内电磁力大小无明显变化。

3 多自由度磁悬浮驱动器的动态特性

3.1 磁悬浮驱动器的控制方案

传统PID控制因其简单、易调节等特性成为了工业生产领域中使用最多的控制器。本文采用传统PID控制器来设计磁悬浮位移控制系统，为达到较好的控制效果需要调整好比例、积分、微分3个参数之间的动态变化关系，其数学表达式为

式中：e（t）为系统误差；kp为比例系数；ki为积分系数；kd为微分函数；G（s）为传递函数。对多自由度磁悬浮驱动器进行阶跃响应仿真分析，分别对z方向的移动、x方向的平动，以及θ方向的转动施加初始值为z=0.2mm，x=0.2mm，θ=10mrad的阶跃进行仿真测试，通过试凑法在闭环中给定系统一个干扰，记录过渡曲线，进行比例环节、积分环节、微分环节逐个调节，直到获得比较理想的控制器参数。z方向kp=43，ki=80，kd=0.45；x方向kp=53，ki=102，kd=0.50；θ方向kp=900，ki=1800，kd=10。仿真结果如图7-9所示。

由阶跃响应仿真结果可知，采用传统PID磁悬浮控制系统对该多自由度磁悬浮驱动器进行控制时，z方向响应时间为0.029s，调节时间为0.1s，超调量为13.3%；x方向响应时间为0.023s，调节时间为0.19s，超调量为24.6%；θ方向响应时间为0.031s，调节时间为0.17s，超调量为20.3%，该控制系统具有一定超调量和较高响应速度。由于微细电火花加工电极与工件间隙的微小变化，传统PID控制超调量较大，难以及时调整，无法满足加工要求。

3.2 模糊PID控制系统

变量较多、结构复杂的系统往往需要进行系统动态简化，而模糊控制是较为合适的系统简化方法，由于Mamdani模糊控制系统中不稳定控制对象的动态性能和稳态性能均有较大提高，所以本文采用经典Mamdani模糊控制系统。该磁悬浮驱动器控制系统为多自由度控制系统，故选择二维模糊控制。二维模糊控制器可以在保证控制精度的同时，避免由于计算规则过于复杂带来的响应结果滞后问题，由于在传统PID控制系统中加入了模糊算法，所以比例系数、积分系数、微分系数都是在原有PID控制基础上加上模糊算法的变化值才能得到最终的修正值，参数修正值计算公式为

模糊控制系统需要定义NB（负大）、NM（负中）、NS（负小）、ZO（零）、PS（正小）、PM（正中）、PB（正大）7个模糊子集。设置两个输出变量为e和ec，论域为[-6，6]。设置3个输出变量为△kp、△ki、△kd，论域为[-3，3]。因为系统要求响应迅速、灵敏度高，所以模糊系统选择三角函数作为系统输入输出隶属函数。建立模糊控制规则是模糊PID控制系统的重要部分，根据控制参数的整定原则以及输入量、输出量之间的关系来确定输出变化量△kp、△ki、△kd的模糊规则，结果如表1-3所示。

确立模糊规则之后进行模糊决策及解模糊化处理，常用的解模糊化方法有最大隶属度法、重心法、取中位数法。重心法又称为加权平均法，即计算输出控制范围内的一系列连续点的重心，而最大隶属度法一般通过平均值、最大值、最小值3种方法获得最终结果。为了使计算量化因子和比例因子更加准确，本文选用重心法计算量化因子及比例因子，结果如表4所示。

使用MATLAB输入以上数据，分别对z、x以及θ自由度进行仿真分析。设定初始位移分别为0.2mm、0.2mm、10mrad，判断仿真模糊PID控制系统是否符合微细电火花电极与工件极间间隙调节条件，需要在0.2s处向x、z方向施加0.1mm、θ方向施加5mrad的阶跃信号。观测仿真曲线在改变位移条件下的调节效果及响应速度，对比传统PID控制系统，仿真结果如图10-12所示。

由仿真图像可知，设置z方向参考位移为0.2mm时，模糊PID控制的响应时间为0.07s，超调量约为5.3%。当在0.2s后施加0.1mm的位移信号时，再次恢复稳定的调节时间为0.09s，超调量约为7.8%；x方向模糊PID响应时间为0.035s，超调量为6.8%，当在0.2s后施加0.1mm的位移信号时，再次恢复稳定的调节时间为0.1s，超调量约为6.5%；设置θ方向参考弧度为10mrad，模糊PID控制的响应时间为0.043s，超调量约为8.7%。当在0.2s后施加5mrad的弧度信号时，再次恢复稳定的调节时间为0.12s，超调量约为8.9%。结果表明，模糊PID控制下的多自由度磁悬浮驱动器动子可以维持动态稳定，在受到干扰之后也能迅速恢复稳定状态。

综合仿真结果可知，磁悬浮驱动器的两种位移控制系统均具备较高的控制精度和较快的响应速度以及较优的跟随效果，采用磁悬浮驱动器结合该控制系统来代替传统电火花加工采用的电机加滚珠丝杠的驱动方式，可以快速调节异常的极间电压，增加加工过程中的有效放电概率，从而提高加工效率。

3.3 多自由度磁悬浮驱动器实验分析

多自由度磁悬浮驱动器位移实验平台如图13所示。实验设备主要包括计算机、dSPACE、直流开关电源、功率放大器、位移传感器、多自由度磁悬浮驱动器。通过端口连接dSPACE实现端口数字信号与模拟信号转换。将高精度位移传感器检测到的位移和位移变化量作为该控制系统的输入变量，经过控制器产生电压信号，经过功率放大器转换为电流信号输出到该磁悬浮驱动器的空心线圈中。

在MATLAB中搭建多自由度磁悬浮驱动器控制框图，对反馈位移进行检测，测试在几个自由度方向上的响应速度以及施加阶跃信号后的调节情况。比例系数、积分系数、微分系数需要依据实验时发生的曲线波动进行实时调节。经过调节后z方向kp=9300，ki=10000，kd=65；x方向kp=8600，ki=9600，kd=55；θ方向kp=660，ki=1200，kd=1.3。在控制系统中分别对几个自由度施加0.2mm、0.2mm、10mrad的阶跃信号，观察在期望位移变化后，该驱动器动子位移响应是否满足电火花电极与工件间隙快速响应并调节的要求，实验结果如图14-16所示。

由阶跃实验结果可知，在传统PID控制系统下，系统恢复z方向动子稳定的调节时间需要0.103s，响应时间为0.028s，超调量为51.5%；模糊PID控制下，系统恢复z方向动子稳定系统调节时间为0.085s，响应时间为0.016s，超调量为38.5%。两者相比，模糊PID控制系统的调节时间较短，响应更快，超调量也较小；x方向PID控制条件下动子稳定的调节时间需要1.2s，响应时间为0.031s，超調量为36.5%。模糊PID控制下，x方向受到干扰的调节时间为0.53s，响应时间为0.023s，超调量为38.5%；θ方向在常规PID控制下，系统恢复θ方向动子稳定的调节时间为0.5s，响应时间为0.21s，超调量为22.0%。模糊PID控制下，系统恢复θ方向动子稳定的调节时间为0.25s，响应时间为0.13s，超调量为7.3%。两者相比，模糊PID控制系统的响应更快，超调量较小。微细电火花要求极间间隙能够在异常放电时进行快速调整，显然模糊PID控制更符合要求。同时，本文增加正弦实验来验证控制系统响应特性，磁悬浮驱动器正弦跟随实验如图17-19所示。

分别对几个自由度进行正弦跟随控制实验可知，传统PID控制系统和模糊PID控制系统正弦信号均能正常跟随，平动定位行程为0.8mm，转动定位行程为40mrad，可用于电火花极间间隙的快速响应，相比于传统PID控制系统，模糊PID控制的跟随效果较好。

4 结束语

本文提出了一种替代传统电火花机床主轴运动的多自由度磁悬浮驱动器结构并对其工作原理进行了阐述。建立了多自由度磁悬浮驱动器动力学模型，基于此模型搭建了控制系统。通过有限元仿真软件，对该磁悬浮驱动器内部空心线圈产生电磁力大小进行了仿真分析。通过设计两种控制方法对磁悬浮驱动器进行了控制系统的仿真研究，通过阶跃与正弦实验验证该磁悬浮驱动器的控制效果。实验结果表明，该多自由度磁悬浮驱动器在不同自由度方向上均有良好的跟随性能与响应速度。当电火花加工极间电压出现异常时，磁悬浮驱动器可以满足极间间隙的快速调整，进而提高电火花加工效率。

（责任编辑：钟媛 英文审校：尹淑英）