基于张量链的电网大数据多模态预测方法

陈彬　徐欢　邹文景

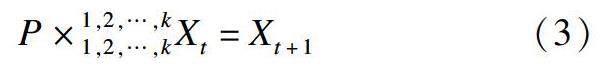
摘要：为了优化大数据预测系统的准确率和运算耗时，在张量理论的基础上，提出了一种适用于电网领域的多模态预测方法。通过综合运用张量和马尔科夫理论，设计了一种具有较强适应性的多元多阶马尔科夫模型，以及无假设前提的马尔科夫转移方法。在此基础上，基于张量链理论的短期预测和长期预测算法，提出了具有较低计算复杂度的大数据多模态预测方法。相关仿真验证结果表明，与经典马尔科夫预测方法相比，基于张量链的多模态预测方法具有更高的预测准确率与更少的运算耗时。

关键词：大数据；张量链；主特征值；多模态预测；并行计算；马尔科夫模型；复杂度分析；预测准确度

中图分类号：TM711 文献标志码：A 文章编号：1000-1646（2024）01-0013-06

随着物联网和云计算等技术的快速发展，智能电网的数据呈现增长迅速、种类广泛、规模扩大和联系复杂等多种特点。在此背景下，传统的表示与分析方法逐渐难以适应电网多种类型数据的实际处理需求。为了实现多种形式数据的处理，研究人员利用张量模型实现多种复杂大数据的表示、处理和分析等过程，这一方法也逐渐被广泛应用于工业、农业和电力等研究领域。然而，电网系统的大数据分析方法仍存在大量的问题未能解决。其中，高维度大数据和硬件设备的低计算能力之间的匹配问题，逐渐成为智能电网中大数据研究所面临的重要问题之一。在硬件设备的计算能力限制下，为了尽量提升高维度大数据的预测准确率，研究者尝试从增量、并行和绿色计算等角度提出相应的预测方法。在增量计算方面，SARWAR等利用奇异值理论，实现快速增长数据流的降维处理与分析；在并行计算方面，DING等在Hadoop模型的基础上，提出了基于张量的高阶奇异值预测算法，从而实现大数据的分布式处理方法；在绿色计算方面，LIN等利用DVFS技术制定了切实可行的任务调度算法，将大数据的预测与分析任务分解至多个计算设备，从而大幅度降低了整体系统的实际能耗。然而，以上预测方法仍难以应对维度不断增加的大数据分析和处理现状，准确率有待提高。

本文通过引入多元马尔科夫模型，提出了多元多阶的马尔科夫转移方法。在张量链的基础上，分别提出了多元马尔科夫的短期预测与长期预测算法，从而大幅提高了电网大数据预测系统的准确率。此外，本文还对预测算法进行了复杂度分析与具体实验，结果表明，所提算法的预测准确率更高且执行时间更短。

1 多元马尔科夫模型

通常一元马尔科夫链主要描述随时间变化的模型状态转移关系。例如，PageRank算法将网站设置为模型的状态，网站之间的跳转动作即为状态的转移动作。随着特征向量的逐渐增多，多元马尔科夫链得到了广泛应用。其核心原理是利用张量和马尔科夫理论，实现多种形式数据的表示以及状态转移的计算。

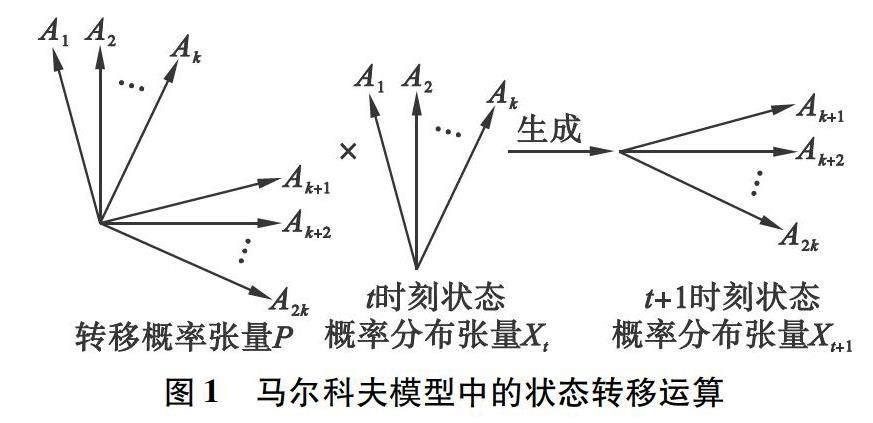
此时，在K阶的维度上，转移概率张量P与t时刻的状态概率分布张量X，进行张量爱因斯坦乘运算，则可获取t+1时刻的状态概率分布张量Xt+1，从而实现模型中的状态转移。

令P表示转移概率张量，Xt和Xt+1分别表示第t和t+1时刻的状态概率分布张量，则状态转移动作的过程可表示为

状态转移的具体运算过程，如图1所示。

2 多元马尔科夫转移方法

由于结合了多种实际影响因素，多元马尔科夫模型可以实现更加精准的预测。在计算过程中，P与Xt之间的阶数并不相同，这大幅降低了爱因斯坦乘的执行效率。为了克服这一问题，本文使用张量链实现马尔科夫模型的存储与计算。原因如下：1）与传统方法相比，基于张量链的爱因斯坦乘只须对低阶张量核进行操作，即可实现并行的混合计算，从而大幅提高张量的计算效率，节省模型的计算时间；2）基于张量链的爱因斯坦乘的计算过程仅需存储具有较低阶数的张量核，其内存开销大幅度减少。总之，基于张量链的多元马尔科夫状态转移模型计算效率高且运行时间短。

3 短期预测算法

利用多元马尔科夫模型，可以极大地缓解高阶张量的维度灾难问题。基于这一原则，本文分别设置用户（A1）、起始时刻（A2）和起始地点（A3）等多种系统状态。在此基础上，提出了基于多元马尔科夫模型的短期预测算法，输入为第t时刻的状态张量Xt和转移张量P；输出为第t+m时刻的状态张量Xt+m，或特定情况的预测结果。具体步骤如下：

1）分别将状态张量X，与转移张量P转换为状态张量链CX't和转移张量链p'；

2）基于状态张量链X't转移张量链P'，利用爱因斯坦乘获取第t+1时刻的状态张量链X't+1；

3）反复运行基于张量链的爱因斯坦乘m次，获取状态张量链X't+m；

4）按照实际问题情况，利用水平并行模式对第t+m时刻的状态张量链X't+m提取相应向量值，并获取各个状态的预测概率值；

5）对所有的预测概率值进行必要的排序，实现短期的多模态预测；

6）输出第t+m时刻的状态张量链X't+m或具体预测结果。

其中，在步骤3）中，基于张量链的爱因斯坦乘可以利用两种混合并行计算的方式实现。通常针对状态张量链X't和转移张量链P'，混合并行计算主要由“先水平后垂直”与“先垂直后水平”组成，则状态张量链X't+1的“先水平后垂直”和“先垂直后水平”规则公式分别为

4 长期预测算法

在多元马尔科夫模型中，利用短期预测算法和f时刻的状態张量链X't，可得到t+m时刻的状态张量链X't+m；而当m趋向于无穷大时，模型使用爱因斯坦乘方法可获取符合稳态分布的转移概率张量链，最终得到相应的主特征张量。在这一过程中，为了避免转移张量出现震荡和过拟合状态，文中对转移张量进行必要的素性修正，令E为平均转移概率张量，β为概率对最终稳态的影响程度，则不可约转移张量P，的素性修正方法可表示为

Pi=βP+（1-β）E （6）

在素性修正预处理后，文中提出爱因斯坦乘的迭代方法，从而完成规范的长期预测算法，输入为转移张量P∈RA1×…×Ak×A1×…×Ah的张量链P‘和收敛阈值δ；输出为转移张量P的主特征张量链X或特定情况的预测结果。具体步骤如下：

1）随机选择初始的状态张量Xo，其元素均为1/（A1×A2×…×Ak），此时∑X0=1；

2）将状态张量X0转换为张量链形式X0；

3）第n时刻的转移张量链X'n由初始状态张量链X'0赋值；

4）将张量链P'和X'n进行爱因斯坦乘运算，使用P'中前k个张量核X'0进行模乘，获取第n+1时刻的X'n+1；

5）计算X'n与X'n+1之间的范数差norm，若norm（X'n+1-X'n）>δ，则转向步骤4）；

6）获取主特征张量链的结果，即令X'=X'n+1；

7）按照实际情况，纤维还原主特征张量链X'，获取预测目标值的概率；

8）按照概率计算结果，对预测结果进行排序；

9）返回目标概率值最大的主特征张量链X'，即获取概率最大的预测结果。

5 复杂度分析

为了进一步实现短期和长期预测的算法对比与分析，设转移张量的维度为I，其张量链的秩为r。文中对短期和长期预测算法的基本步骤进行必要的复杂度分析。

首先，短期和长期预测算法均须对状态概率张量进行张量链的分解动作。在短期和长期预测算法中，设第n时刻的状态概率张量为Xn，坐标为（i1，i2，…，ik）的张量元素被设置为1，其余均为0，则其张量链的秩为l，每个张量核中X（i，ik，1）=1，且操作的时间复杂度均为O（1）。

其次，短期和长期预测算法须利用张量链完成爱因斯坦乘运算。若选择“先垂直后水平”的计算方式，其顺序为：1）该算法须执行1bk个时间复杂度为O（r6）的四阶张量的多模乘；2）算法须执行，次复杂度为O（r4）的三阶张量的多模乘运算，即该算法的单次迭代时间复杂度为O（r61bk+Ir4）。同理，利用同样的分析方法，使用“先水平后垂直”的计算顺序。该算法具有更高的执行效率，其时间复杂度为O（Ik/2+1r3+2Ikr2）。

最终，短期和长期预测算法均须在指定的模态下执行纤维还原。在纤维还原的过程中，算法须执行，I1bk次三阶张量的通信操作，而每次的时间复杂度为O（r3），单次的时间复杂度为O（Ir31bk）。

总之，若选择“先垂直后水平”的计算顺序，短期和长期预测算法执行M次转移，其总体时间复杂度为O（M（r61bk+Ir4）+Ir31bk）；若选择“先水平后垂直”的计算顺序，则算法执行M次转移的总体时间复杂度为O（M（/k/2+1r3+2Ikr2）+Ir31bk）。通过这两种时间复杂度的比较可知，当状态概率分布张量的阶数k较小时，预测算法使用“先水平后垂直”计算顺序的时间复杂度更低，且执行效率更高；而当k较大时，预测算法使用“先垂直后水平”计算顺序的时间复杂度更低，其具有更高的执行效率。

6 仿真实验

为了验证和测试基于张量链的多模态预测算法，本文使用预测准确度与运算耗时等评价指标，对传统预测算法和基于张量链的多模态预测算法进行对比。

6.1 实验设计

在实验硬件方面，本文使用6台型号为IntelXeon E5-2630的服务器主机，利用局域网进行连接形成集群，其包含1台内存为125GB的Master主机和5台内存为50GB的Slave主机；在实验数据方面，本文选用来自于微软亚洲研究院的GeoLife数据集，该数据集由11个用户在一定空间范围之内的GPS轨迹数据组成，兴趣点为226个；在时间维度上，将这些用户的某一天轨迹数据分为4、6、8、10和12等多个时间段。实验将90%的GeoLife数据集作为训练数据，剩余的10%作为测试数据，从而完成传统预测算法、高阶奇异值预测算法与基于张量链的多模态预测算法的多项参数对比。需要说明的是，设由K个元素组成的预测结果集合为Qs={v1，v2，…，vk}，由n个元素组成的测试目标序列集合为T={T1，T2，…，Tn}，若测试目标序列集合Ts中的任何一个元素Ti∈Qs，则预测结果命中一次。通过总结预测结果集合的命中次数，可以衡量其预测准确率。第i个测试集元素Ti的命中次数的计算方法如式（7）所示。通过计算所有的测试目标序列集合的命中次数，可计算出预测算法的预测准确率，具体计算方法如式（8）所示。

6.2 短期预测实验对比

为了验证基于张量链的短期预测算法的准确率和运算耗时，本文通过选取相同的数据分解精度（10-5），利用不同数量的预测结果集合，获取不同预测算法的准确率与运算耗时结果，从而充分地比较经典马尔科夫预测方法、高阶奇异值预测算法和基于张量链的短期预测算法。预测准确率与运算耗时的统计结果，分别如图2、3所示。

从图2中可以看出，在预测算法的运行过程中，当预测结果集合数量增加时，经典预测算法、高阶奇异值预测算法与基于张量链的短期预测算法的预测准确率均逐渐提高。但短期预测算法和高阶奇异值预测算法的准确率提升速度更快，经典预测算法的准确率上升较慢，当预测结果集合数量相同时，与经典预测算法和高阶奇异值预测算法相比，短期预测算法具有更高的预测准确率。从图3中可以看出，随着预测结果集合数量的增加，经典预测算法的运算耗时逐渐增加，当预测结果集合数量大于5之后，经典预测算法的运算耗时急剧增加。与经典预测算法不同的是，高阶奇异值预测算法和短期预测算法在预测结果集合数量达到3之后，其運算耗时不再有明显增长，分别稳定在15s和11s左右，此外，当预测结果集合数量相等时，与高阶奇异值预测算法相比，短期预测算法具有较低的运行耗时。换言之，短期预测算法的运算耗时普遍较低，且几乎不受预测结果集合数量的影响。综上所述，与经典马尔科夫预测算法和高阶奇异值预测算法相比，在相同的仿真实验条件下，基于张量链的短期预测算法具有更高的预测准确率与更低的运算耗时。

6.3 长期预测实验对比

与短期预测算法的验证过程相似，本文也对长期预测算法进行了必要的验证与比较。即在不同数量的预测结果集合条件下，对比经典马尔科夫预测算法、高阶奇异值预测算法和基于张量链的长期预测算法的预测准确率与运算耗时，结果如图4、5所示。

从图4中可以看出，随着预测结果集合数量的逐渐增加，经典预测算法、高阶奇异值预测算法和基于张量链的长期预测算法的预测准确率逐渐提高，且后者的提升速度更快。与经典预测算法和高阶奇异值预测算法相比，当预测结果集合数量相同时，长期预测算法的准确率更高。从图5中可以看出，随着预测结果集合数量的增加，经典预测算法的运算耗时不断增长，且其提升速度也逐渐增加。当预测结果集合数量达到2之后，长期预测算法的运算耗时基本达到平稳，其数值大约为500s，当预测结果集合数量达到6之后，高阶奇异值预测算法的运算耗时约为1000s。当预测结果集合数量相等时，与高阶奇异值预测算法和经典预测算法相比，长期预测算法的运算耗时更少。综上所述，与经典预测算法和高阶奇异值预测算法相比，基于张量链的长期预测算法具有更高的预测准确率与更少的运算耗时。

7 结束语

在张量链理论的基础上，本文提出了适用于电网大数据分析的短期预测和长期预测算法。相关仿真实验结果表明，在预测准确率和运算耗时指标方面，基于张量链的多模态预测算法优于经典的马尔科夫预测算法。然而，由于受实验环境和硬件设备等外部条件的限制，本文未能实现多种预测算法的运行内存统计与对比，这将影响所提预测算法的实际应用和推广，后续的研究会解决这一问题。

（责任编辑：杨树英 文审校：尹淑英）