基于改进NSGA-Ⅱ的破损沉船起吊力优化

程志友,谢佳宏,李亚玲

(1. 重庆交通大学 航运与船舶工程学院,重庆 400074;2. 重庆交通大学 经济与管理学院,重庆 400074)

0 引 言

部分破损沉船打捞工程具有较高的风险性。由于船体破损导致结构强度降低,一旦起吊时内力过大,导致沉船起吊断裂,则需要二次打捞,不仅造成经济损失,还可能引发海洋污染等诸多严重后果。因此,通过优化起吊力参数来降低沉船起吊时的内力,避免沉船起吊断裂是提高沉船打捞安全性的一项重要研究内容。

王高阳等[1]以某30万t VLCC实船为例,选取横舱壁移动距离和货油质量分布曲线控制点坐标为设计变量,以计算工况中的最大静水弯矩值最小为目标,建立了优化模型,并采用组合优化算法进行优化计算,有效降低了静水弯矩;杜尊峰等[2]采用改进的多目标遗传算法优化各压载水舱调配后的压载水量,有效缩短了荷载传递时间并减小了总纵向弯矩,具有一定的工程应用价值。

现有关于降低船舶内力的研究多以正常船舶为对象,以其静水弯矩作为优化目标且以沉船为对象的研究相对较少。此外,正常船舶的船体结构完整,一般仅考虑弯矩也能满足要求。但沉船船体结构往往存在严重破损,为降低沉船起吊断裂风险,需要同时降低沉船的剪力和弯矩。

当前,NSGA-Ⅱ算法[3]是解决多目标优化问题的经典算法之一,它在NSGA算法的基础上引入了快速非支配排序和拥挤度计算,降低了算法的时间复杂度,还引入精英策略,提高了子代种群的多样性。

综上,为降低沉船起吊时的内力,从梁弯曲理论出发,针对沉船起吊受力特点建立了以起吊力参数为输入参数的沉船内力数值计算模型;基于该计算模型,以起吊力参数为优化变量,以内力峰值为优化目标,建立了起吊力参数优化模型;采用改进的NSGA-Ⅱ算法进行优化计算,为沉船打捞提供参考。

1 工程概况

某工程案例中[4],沉船基本资料如下:沉船主尺度为92.95 m×14.8 m×7.5 m,船体水中重量约为1 607 t(文中提到的重量均指水中重量),重心为舯后7.42 m。此外,该沉船内有两处剩余货物,其重量分别为143、286 t,其重心分别位于舯前22.65 m和舯后3.14 m。沉船受损情况如下:距尾垂线约25 m处有一个长度约为7 m的破洞,该处下部双层底已经破损,沉船完全进水。

对于资料不足的沉船,其重量分布可使用比雷斯梯形曲线近似表示[5-6],如图1。

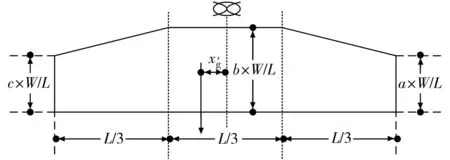
图1 比雷斯梯形曲线Fig. 1 Bires trapezoidal curve

图1中,W为重量,L为船长(取93 m),x′g为重心位置,a、b、c为比雷斯系数。该船为肥型船舶,故取b=1.174。a、c如式(1):

(1)

参考工程经验,使用两对1 200 t浮筒打捞沉船,浮筒1围绕破洞中心布置,避免破洞部分的内力过大,浮筒2布置在舯前的适当位置。每对浮筒对称分布在沉船两侧,提供相同大小的力。货物及浮筒在沉船上的分布示意如图2。

图2 货物及浮筒的分布示意(单位:m)Fig. 2 Distribution diagram of cargo and buoy

每对浮筒通过对称分布的4根过船底吊缆对沉船施加吊力,如图3。

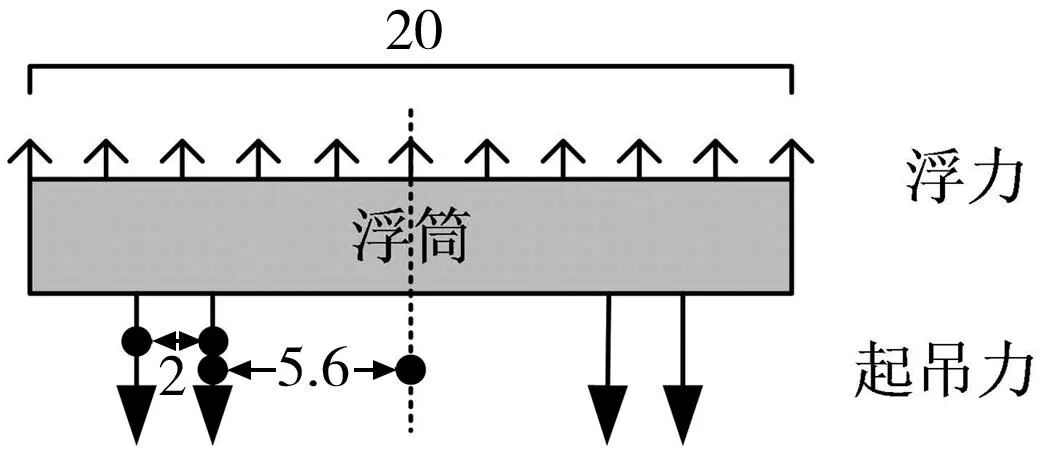
图3 浮筒受力示意(单位:m)Fig. 3 Diagram of the force on the buoy

在水下起吊阶段,沉船离底最后时刻的受力达到最大,也最危险,故取该时刻的沉船为研究对象。实际工程中会控制倾角,较小倾角可以忽略,其受力如图4。

图 4 沉船受力示意Fig. 4 Diagram of force on shipwreck

需要指出的是,文献[4]中仅计算了几处关键弯矩且部分数据未展示。为了清楚表达优化效果,笔者对部分缺失数据进行了合理取值。

2 沉船内力数值计算模型

沉船与正常船舶的受载存在明显不同:正常船舶在重力与浮力的共同作用下保持平衡,而沉船的上升力主要由起吊力提供。因此,需要根据沉船受力特点建立沉船内力数值计算模型。

2.1 受载分类

将该沉船受载分为Fz、Qz两类。Fz为吊缆对沉船施加的起吊力合力(图4)。Qz为除起吊力以外其他所有载荷的等效力,包括船体以及货物的重力、吸附力等。Fz与Qz大小相等,方向相反,g=9.8 N/kg。

2.2 受载计算

常用吊缆的直径约为0.1～0.2 m,其相对于船长较小,故可视Fz为集中力,其大小由吊缆直接提供。Qz由多个分布力组成,其分布曲线Q(x)可以按照以下方式计算[5]:

1)由沉船基本参数和比雷斯系数可以得到表示船体重量分布曲线的三等分比雷斯梯形曲线。

2)使用梯形曲线将沉船剩余货物的重量分别等效到沉船三等分后的艏段和舯段,得到剩余货物重量分布曲线。

3)吸附力大小可由打捞重量(船体重量+剩余货物重量)与吸附力系数相乘近似得到。海底底质为砂石及沙底,且沉船陷入较浅,参考工程经验[7]取吸附力系数为0.2。此外,假设海底土壤与船底接触均匀,吸附力沿船长平均分布。

三者叠加即可得到Q(x),如图5。

图5 等效力分布曲线Q(x)Fig. 5 Equal potency distribution curve Q(x)

2.3 内力计算方法

按一般的20站计算法[8]计算船舶内力时,需要将起吊力等效为相邻站上的分布载荷,而吊缆的直径相对于站距而言较小,故将其视为集中力,直接计算沉船内力更为合理。此外,避免对起吊力进行等效处理还有利于减少计算步骤,提高后续使用优化算法的迭代效率。

计算船舶内力时,可将船体视为箱体梁。根据梁弯曲理论进行计算,边界条件均为完全自由端[6,8],即两端的剪力和弯矩均为0。由2.2节得到Q(x)的函数表达式为:

(2)

式中:q1(x)、q2(x)、q3(x)分别为艉段、舯段、艏段上等效力分布曲线的函数表达式。

将Fz、Qz各自视为一个整体,以左端点(尾垂线所在位置)为原点可得内力曲线方程:

(3)

(4)

式中:xi为第i个起吊力的位置参数,即第i个起吊力与左端点的距离;fi为第i个起吊力的大小参数,与xi一一对应,每一个起吊力的位置参数和大小参数并称为一组起吊力参数,多组起吊力参数统称为起吊力参数;n为起吊力的个数,即有n组起吊力参数;Fd(x)为0～x段上Qz的合力;Md(x)为0～x段上Qz对x处的合力矩;N(x)为沉船剪力曲线;M(x)为沉船弯矩曲线。

该计算方法的思路是先计算Fz、Qz各自引起的剪力曲线和弯矩曲线,然后叠加得到沉船的内力曲线。该计算方法避开了将起吊力等效为分布载荷,使得计算更加合理,同时也减少了计算步骤,提高了优化迭代的效率。

2.4 任意站面的内力计算

为方便编程计算,将式(3)、式(4)进行离散化处理。首先,将沉船沿船长分为m个单元,获得m+1个截面。然后使用m+1维向量X表示x,则X的每个分量均表示沉船的一个截面,计算出X对应的剪力向量N(X)和弯矩向量M(X),即可得到各截面上的剪力和弯矩。其中,首尾两个端面上的内力均为0。设Q(x)、Fd(x)、Md(x)分别由m+1维向量Q(X)、Fd(X)、Md(X)表示,可得到沉船内力数值计算模型:

N(X)=Fd(X)-Fu(X)

(5)

M(X)=Md(X)-Mu(X)

(6)

式中:Fd(X)为Fz引起的剪力分布;Md(X)为Fz引起的弯矩分布。

若m取值越大,则单元长度|ΔX|=L/m越小,精度越高,但相应的计算速度会降低。常用吊缆的直径约为0.1～0.2 m,故取|ΔX| =0.000 1L(约0.01 m)较为合适。此时,式(5)、式(6)较式(3)、式(4)的相对误差约为 ±0.05%。

3 起吊力参数优化模型

3.1 目标函数

要降低沉船起吊断裂风险,需要使内力峰值尽可能小,而内力的正负仅表示方向,不表示大小,故以内力峰值最小为优化目标即可得到关于剪力和弯矩的两个目标函数:

(7)

式中:(xi,fi)为第i组起吊力参数,表示第i个起吊力的位置和大小,共n组;|N(X)|为剪力绝对值向量;|M(X)|为弯矩绝对值向量。

3.2 约束条件

约束条件如下:

1)平衡起吊要求:沉船起吊过程保持平衡,满足静平衡方程,忽略横向载荷影响,故仅有两个静平衡方程。

2)破损部位的弯矩方向要求:破损部位的弯矩方向不得利于发生裂纹扩展,若破损开口向上,则破损部位的弯矩应该小于0;反之,破损部位的弯矩应该大于0。

3)变量范围要求:xi理论取值范围为0～L,而fi理论取值范围为0～Fz。考虑到局部强度,xi不得取到破损部位。

4)其他要求:沉船起浮方式较多,不同起浮方式的起吊力参数限制也不同[9]。采用两对浮筒起浮的限制较多(图3),设同一浮筒上的起吊力位置相对固定,同一浮筒上的起吊力大小相等。

综上,约束条件的数学表达式为:

(8)

式中:xg为等效力Qz的重心与沉船左端点的距离;XP∈[21,29]为破损部位对应的截面向量;M(XP)为破损部位的弯矩向量。

3.3 NSGA-Ⅱ算法改进

内力优化包含剪力和弯矩两个目标,属于多目标优化问题。NSGA-Ⅱ 算法作为常见的多目标优化算法,其寻优部分与基本遗传算法并无差别。基本遗传算法可以不依赖问题信息进行寻优,但存在早熟问题,故需要结合内力数值计算模型特点对其做出改进。

3.3.1 划分种群,独立交叉

由于起吊力参数优化模型同时包含xi和fi两种优化变量,若两者进行相互交叉,则容易相互干扰,丢失各自的优秀基因,导致早熟。故当算法执行到交叉时,将种群分割成两个子种群,各自独立进行交叉后,再组合成新的子代种群。

3.3.2 引入模拟退火算法思想

各组起吊力参数之间的顺序关系并不唯一,故存在最终效果相同的不同解集,导致对种群进化过程产生干扰。为此,引入模拟退火算法思想[10],将变异概率p和交叉概率c视为模拟退火算法中的温度,其随着迭代次数增多而降低,使得算法在前期有较高的p和c,尽可能对整个空间进行搜索,提高种群的多样性。而后期p和c逐渐降低,种群尽可能保留前面积累的优秀个体,重点进行小范围内的局部搜索。设温度下降系数为t,则改进后的算法流程如图6。

图6 改进的算法流程Fig. 6 Improved algorithm flow chart

4 计算结果及对比分析

4.1 计算结果

通过MATLAB实现优化计算,算法主要参数设置如下:种群大小为200,迭代次数为500,选择概率为0.8,变异概率为0.5,交叉概率为0.8,温度下降系数为0.987。计算出Pareto最优解集对应的Pareto前沿,如图7。

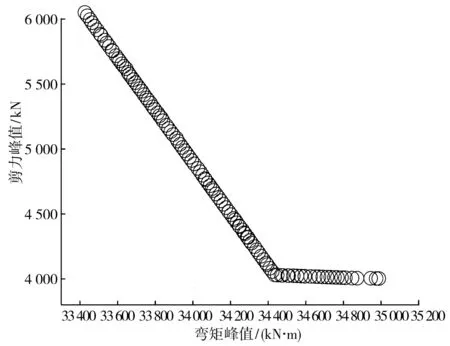
图7 Pareto前沿Fig. 7 Pareto front

由图7可知:剪力峰值最大为6 050.97 kN,此时的弯矩峰值最小,其值为33 425.82 kN·m;剪力峰值最小为4 003.00 kN,此时的弯矩峰值最大,其值为34 990.82 kN·m。综合考虑剪力和弯矩,取Pareto前沿拐点对应的解作为优化计算后的起吊力参数代表,与按照经验布置的起吊力参数作对比。

4.2 结果对比分析

按照工程经验布置的起吊力参数,记为经验方案;优化计算出的起吊力参数,记为优化方案。两种方案的起吊力参数及内力峰值见表1。

表1 起吊参数及内力峰值对比

由表1可知,优化后的剪力峰值下降了约22.72%,弯矩峰值下降了约16.13%。由此可见,改进后的优化算法对于降低沉船内力有比较明显的效果,其优化计算出的解对破损沉船打捞的起吊力布置具有较大的参考价值。

5 结 语

从梁弯曲理论出发,针对沉船起吊受力特点建立了以起吊力参数为输入,以内力分布为输出的沉船内力数值计算模型。该计算模型较20站计算法更为合理,可以作为独立模块计算任意起吊力参数下的沉船内力,其计算精度可以根据需求进行调整。

基于沉船内力数值计算模型,以起吊力参数为优化变量,以内力峰值为优化目标,建立了起吊力参数优化模型;采用改进的NSGA-Ⅱ算法进行优化计算,计算出了降低沉船内力的起吊力参数。将该优化模型应用于实际工程时,应注意以下两点:

1)对于涉及到舱室未完全浸水产生内浮力的工况,只需要将内浮力曲线叠加到分布曲线Q(x)中即可,后续优化流程不变。

2)对于需要考虑其他客观因素对起吊力参数的限制时,只需要在优化模型的约束条件中添加相应的约束即可,后续优化流程不变。

此外,该优化模型可以同时优化剪力和弯矩,而对于其计算出的Pareto解集,也应该综合沉船的整体状态,针对性选择起吊力参数,尽可能降低沉船起吊断裂的风险。