轨道交通单线接运电动公交调度优化模型

杨亚璪,吴 钊,宾 涛

(1. 重庆交通大学 交通运输学院,重庆 400074;2. 江苏纬信工程咨询有限公司,江苏 南京 210014;3. 重庆交通大学 智能综合立体交通重庆市重点实验室,重庆 400074)

0 引 言

根据交通运输部数据,截至2022年末,全国54个城市开通运营城市轨道交通线路共292条,运营里程为9 554.6 km;同时,公共汽电车运营线路开通7.8万条,公共汽电车70.32万辆,其中纯电动车45.55万辆,占比64.8%。电动公交凭借其节能、低碳等优势逐渐确立了在城市公交运营中的主体地位。与传统燃油公交相比,电动公交尚存在续航时间不能满足全日运行、充电周期长等问题,对公交车辆的调度造成较大影响。轨道交通作为城市公共交通的重要组成部分,轨道交通站点的影响范围较大,部分乘客在轨道交通站点存在换乘接运公交前往目的地的需求。通过对接运电动公交与轨道交通的乘客接运关系进行分析,建立接运电动公交更优调度模型,对提高乘客运输效率与满意度等具有积极意义。

在电动公交的调度优化模型构建方面,TANG Xindi等[1]分别构建了动、静态两种模型,将时间与道路状况的随机性考虑在内,对电动公交车队进行周期性安排;T.PAUL等[2]从整体电网供电状态出发,将电动公交与化石燃料公交一同进行调度,并给出了电动公交的充电计划;C.M.CHAN等[3]从配电网有限的条件出发,以优化接运电动公交配置为目标,构建了离散非线性优化模型来解决电动公交车辆的配置问题;唐春艳等[4]考虑不同电动车车型的运营差异,构建多目标优化模型,研究了不同车型混合使用情况下的发车时刻表;ZHU Chao等[5]建立具有特定约束条件的单车场车辆调度模型来解决电动汽车调度问题;J.P.FONSECA等[6]将发车时刻表和车辆调度问题同时考虑,构建了一个转移成本和运行成本最小化的双目标混合整数规划模型。

公交调度和车辆调度问题是NP-hard问题,A.S.PEPIN等[7]采用5种不同的启发式算法进行对比分析,认为大领域搜索启发式算法解决公交调度问题最有效;SHEN Yindong等[8]通过使用领域搜索法与一种改进的禁忌搜索算法对车辆与驾驶员调度模型进行求解;ZHANG Le等[9]、刘昊翔等[10]采用列生成算法对构建的模型进行求解;DOU Xueping等[11]采用人工蜂群算法对所构建的模型进行求解,并通过对比发现该算法的收敛性较好。

综上,目前的研究主要关注电动公交自身运营的调度策略,构建的优化模型中主要考虑充电、成本等约束条件,并采用启发式算法对所构建的模型求解。

笔者拟通过对电动公交与轨道交通接运关系的分析,构建一个混合整数非线性规划(mixed integer nonlinear programming,MINLP)模型,以实现3个目标:①尽量减少已服务乘客的总等候时间成本;②将未服务乘客的换乘失败成本降至最低;③使公交公司的总运营成本最小。利用人工蜂群算法(artificial bee colony algorithm,ABC)求解模型,给出接运电动公交的调度策略与最优发车时刻表,为接运电动公交调度问题提供解决思路。

1 问题描述

常规公交是公共交通方式的重要组成部分,常规公交与轨道交通之间存在交互胁迫的关系[12]。在公共交通网络中,轨道交通是“骨架”,而常规公交则用于满足沿线居民的短途出行需求。

轨道交通与常规公交的换乘模式主要分为站内换乘、接续换乘、站外换乘[13],文中主要研究的换乘模式为站外换乘。当地面公交沿线的出行需求中加入了轨道交通换乘需求时,原有的调度策略会出现不能适应的情况。此时,地面公交被赋予接运属性,即公交车辆到达接驳站点时,需要为有换乘需求的乘客提供足量、及时和有效服务。

假设轨道交通站200 m范围内存在接运电动公交停靠站,乘客可从轨道交通换乘至电动公交。换乘乘客由于步行速度不同,从轨道交通站步行至电动公交站的时间为1.5～3.0 min,而乘客能够接受的等待时间最长为8 min。早高峰08:00—08:30内,共有6辆电动公交与同时段抵达的5列轨道交通列车形成接运关系,见图1。由于两类车辆到站时刻、换乘乘客步行时间的差异,接运电动公交采用怎样的调度策略提升乘客换乘的满意度,同时兼顾公交企业的运营成本,此为文中主要研究问题。

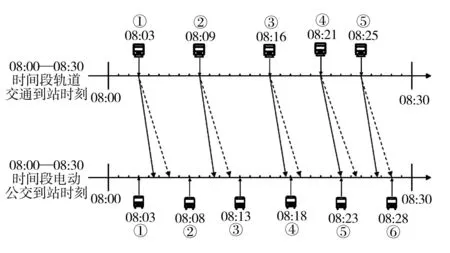
图1 电动公交与轨道交通接运关系Fig. 1 Relation between electric feeder bus and rail transit

2 建立模型

2.1 基本假设

为反映真实情况,作以下基本假设:①轨道交通的列车运行严格执行预先计划的时间表,到站时刻没有延误和提前;②选择换乘接运公交线路的乘客,只有在超过等待时间上限后,才会考虑选择其他方式离开接运站点;③换乘乘客从轨道交通站步行至电动公交站所需时间根据现场测算给出;④每辆电动公交的容量一致,区别在于到达接运站点时的满载率不同;⑤如果换乘乘客排队,则按照电动公交的最大载客量进行核减后,确定成功换乘的乘客数量。

2.2 目标函数

令SB为服务于目标接运公交线路的公交班次集合,J为SB内可用接运公交的行程总数,j为可用的接运电动公交行程序号,j=1,2,…,J;令SR为某一时段内轨道交通列车到达的集合,I为SR内轨道交通列车的到达行程总数,i为轨道交通列车的到达车次,i=1,2,…,I。以每次行程中接运电动公交j的发车时间dj和荷电状态Oj为决策变量,以乘客和公交企业的广义成本z为目标函数:

minz=zw+zf+zo+zc

(1)

在给定时间段内,乘坐接运电动公交j的乘客总等待时间成本zw如式(2):

(2)

式中:μ1为总等待时间成本的单位值,元/min;sij为实际从i列车转移到接运公交j的乘客数量,人;dj为接运电动公交j的发车时刻;Ai为轨道交通列车i的换乘乘客抵达公交车站时刻。

在给定时间内换乘失败的乘客换乘总失败成本zf见式(3):

(3)

式中:μ2为总转移失败成本的单位值,元/人;Pi为轨道交通列车i产生的换乘需求。

公交公司的运营成本分为接运电动公交的使用成本与充电成本,其中接运电动公交的车辆使用成本zo见式(4):

(4)

式中:μ3为接运电动公交使用成本的单位值,元;φ为电动公交车辆使用的年化系数;Yj为0、1变量,若行程j被接运电动公交执行则Yj=1,否则Yj=0。

接运电动公交的充电成本zc见式(5):

(5)

式中:μ4为充电成本的单位值,元/(kW·h);εj为二元变量,用作判断是否需要充电的依据;Oj为电池的荷电状态,指电池在一定的放电倍率下,剩余电量与相同条件下额定容量的比值;Du为电动公交u的电池容量,kW;lj为需要被执行行程j的里程,km;C为电动公交车行驶过程中电量的平均消耗速率,(kW·h)/km。

式(5)中,设置的公交电池荷电状态的最大、最小值分别为Omax和Omin。每一班电动公交发车时检查荷电状态Oj,若Oj≤Omin或OminOmax时,则停止充电;当Oj≥lj·C/Du时,则不需要充电,充电与否通过0、1变量εj判断。

2.3 约 束

设dj为在给定时间段内为l线服务的接运公交j的到站时间,见式(6)～式(9):

dj=dj-1+hj-1,j=2,3,…,J

(6)

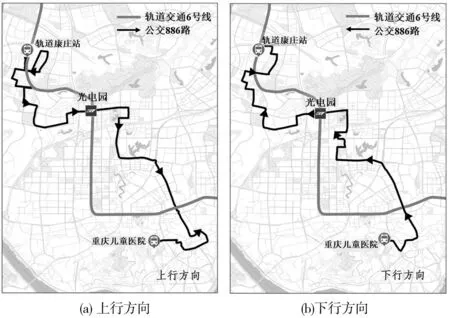
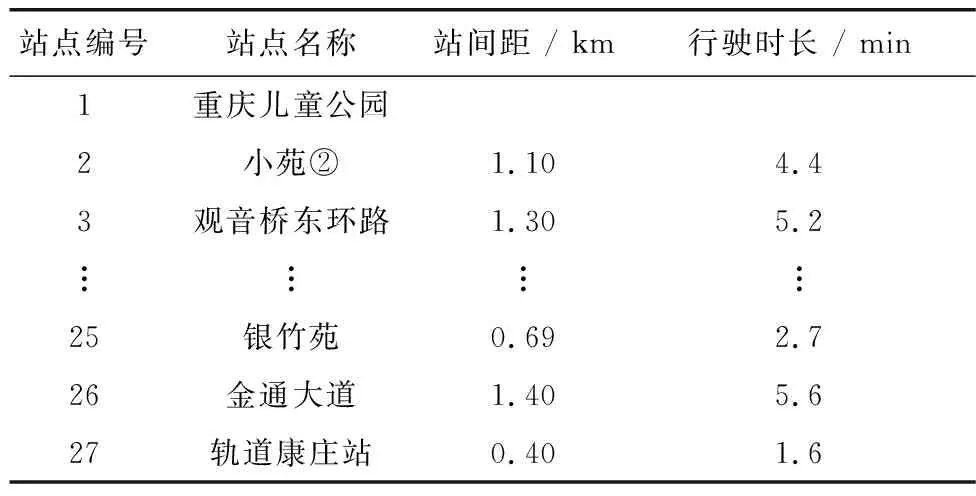
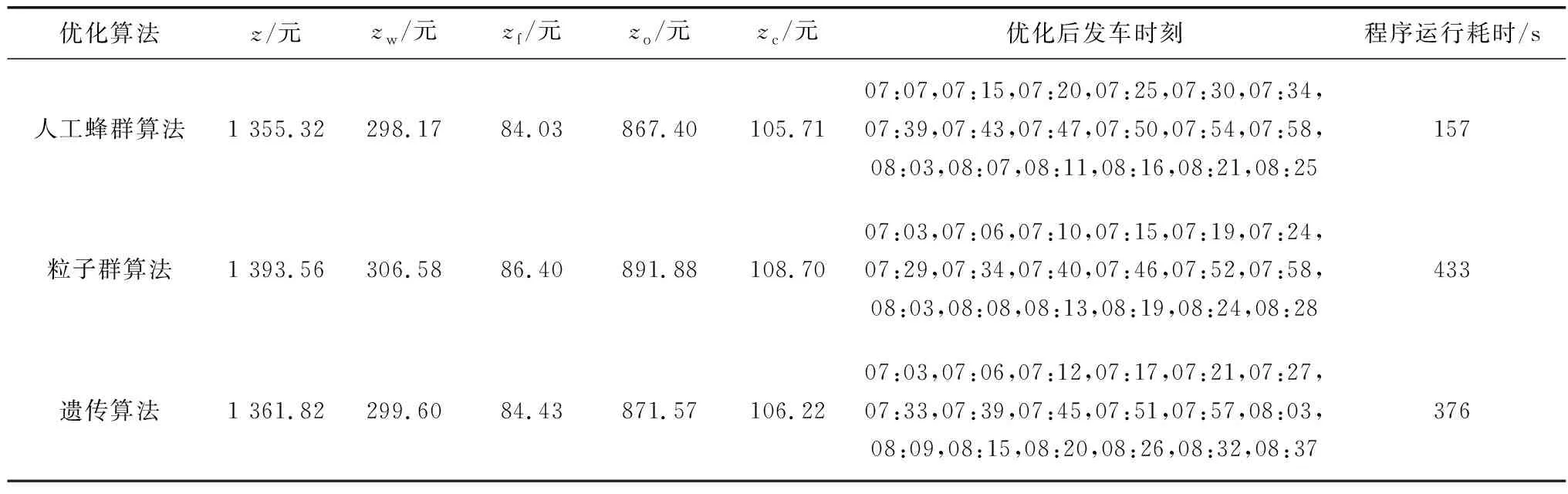
Tmin≤d1

(7)

Hmin≤hj≤Hmax,j=1,2,…,J-1

(8)

d1,hj∈Z+,j=1,2,…,J-1

(9)

式中:hj-1为接运电动公交j-1与j之间的间隔时间,min;Tmin为给定时间段的开始时间,min;Hmin、Hmax分别为最小和最大允许间隔时间,min;Z+为一组正整数。式(7)迫使接运公交线路l的第一班车在给定时间段内发车;式(8)保证了时刻表的实用性。可供使用的接运电动公交车数量应不少于J=「TP/Hmin⎤,其中TP为给定时间段的持续时间。为便于实际公交运行,将终点站出发时间和发车间隔设置为整数变量,如式(9)。

当接运公交j的终点站出发时间和来自列车i的乘客到达公共汽车终点站的时间之间的差值为非负数时,来自列车i的乘客有机会登上接运公交j。二元变量yij用来表示来自列车i的乘客是否有机会登上接运公交j,见式(10)、式(11):

yij∈{0,1}

(10)

M·(yij-1)≤dj-Ai

(11)

式中:i=1,2,…,I;j=1,2,…,J;M为一天24 h的分钟数,M=1 440;Ai为来自列车i的乘客到达接运公交车站的时间。如果来自列车i的乘客有机会登上接运公交j,则二进制变量yij为1,否则为0。

由于接运公交的载客量固定,yij=1时,但是来自列车i的乘客可能无法登上接运公交j。当yij=1且接运公交j上有可用空间时,来自i列车的乘客将被允许登上接运公交j。sij见式(12):

(12)

当乘客从列车i开始登上接运公交j时,接运公交j上的乘客人数见式(13):

(13)

(14)

式中:i=1,2,…,I;j=1,2,…,J;wij为接运公交j-1被调度后,等待接运公交j的来自列车i的乘客数量;Lij为在接运公交j调度前已经停止等待接运公交j的来自列车i的乘客数量。变量wij与Lij见式(15)、式(16):

(15)

Lij=⎣wij·xij·α」

(16)

式中:i=1,2,…,I;j=1,2,…,J;pi为列车i排队的乘客人数;⎣ 」表示该数字应该向下舍入,以确保Lij是整数变量;xij为二元变量,当接运公交j的出发时刻与列车i乘客的到达时刻之差大于TL时,xij=1,否则xij=0,见式(17)、式(18):

M·(xij-1)

(17)

xij∈{0,1}

(18)

式中:i=1,2,…,I;j=1,2,…,J。

第i列车乘客中参与排队的乘客数量见式(19):

pi=βPi-βmin{max{Q-qi,0},P}+min{max{Q-qi,0},P}

(19)

式中:i=1,2,…,I;qi为从i列车上下来的乘客到换乘站点时队伍的长度;Q为最长可容忍排队长度;β为乘客加入队列的概率。由式(19)可知,当qiQ时,β<1。qi见式(20):

(20)

3 求解算法

ABC算法是一种基于蜜蜂群觅食行为的启发式算法,其中被称为食物源的解决方案由人工蜜蜂随时间修改,蜜蜂的目标是发现具有较高花蜜量的食物源[14]。ABC算法已被广泛应用于解决公交优化问题[15-16]。

3.1 算法描述

在给定起点站发车时间与接运电动公交容量的情况下,根据蜂群算法的原理可得出,一个解决方案(即一个食物源)由2J-1个元素组成,代表了J-1个时间间隔和J班次电动公交车出发时的荷电状态,见图2。

图2 解决方案示意Fig. 2 Schematic diagram of the solution scheme

每个元素ej是一个介于0和1之间的随机数,由伪随机数发生器产生。根据算法设计流程,接运电动公交在站点处发车时间间隔的解码原理为hj=⎣Hmin+(Hmax-Hmin)」×ej。电动公交荷电状态的解码原理如下:当e2J-1满足Oj≤Omin或OjOmin后发车;当e2J-1满足Oj>Omax时,无须充电直接发车。

3.2 算法步骤

步骤1初始化食物源Nf的数量、雇佣蜂Ne的数量、观察蜂No的数量、预定的试验次数限制和最大迭代次数Nmax,设迭代次数的计数器N=1。

步骤2将雇佣蜂Ne与食物源一一对应,为每只蜜蜂随机生成一个2J-1维的可能解,并计算其适应度值fi=1/(1+zi),其中,zi为该电动公交运营时刻表下的总成本。

步骤4对于剩余的蜜蜂,在食物源附近进行邻域搜索,寻找新的食物源。

步骤5计算新生成食物源的适应度值并进行评估,记录当前蜜蜂寻找到的最优食物源信息,即发车时刻方案。

步骤6当N>Nmax时,终止算法并输出最优解;否则,设置N=N+1,重复步骤3～步骤5。

4 算 例

重庆两江公交886路作为与轨道交通6号线光电园站点的接运电动公交,主要承担轨道交通线路之间的换乘及轨道交通站点到渝北区光电园周边各大写字楼之间的乘客疏解功能,如图3。

图3 重庆两江公交886路上下行路线Fig. 3 Upward and downward routes of Chongqing Liangjiang bus route 886

公交886路下行(轨道康庄站—重庆儿童公园)06:10开班,21:00收班;其上行(重庆儿童公园—轨道康庄站)早上06:30开班,21:00收班,全程16.7 km,途经24个站点。路线全线运营平均耗时68 min,站间距及站间行驶时长如表1。其中,该线路在软件园渝兴广场站实现与轨道6号线光电园站换乘,主要连接山顶总部基地、服务贸易产业园、互联网产业园3个工作集散地。

表1 886路公交站间距及站间运营时间

车辆规格方面,866路公交车采用宇通ZK6117BEV纯电动客车,座位数为35个,满载人数cj=60人,电池容量Du=180 kW·h,设Omin=0.2。该电动客车在满电量情况下行驶里程lj≥130 km。重庆市工作日早高峰公交车行驶速度约为14.1 km/h,公交优先道的车速约为15.8 km/h,可以计算电量平均消耗速率C=1.38 (kW·h)/km,额定充电功率取120 kW,充电效率为0.9。

假设乘客刷卡出站后步行至公交站所用时间为2 min,乘客换乘后需要乘坐公交在上班时间前抵达公司附近公交站。以终点为互联网产业园附近的乘客为例,需要其至少在08:30前抵达换乘公交站,乘坐公交车前往公司。轨道交通6号线在光电园站共有53趟地铁列车在07:00—08:30时间段内到达,相关班次的地铁到达时间见表2。

表2 重庆轨道交通6号线光电园站车辆运行时刻

假设该公交站点本地乘客的平均到达率λ=2 prs/min,给定时段内允许的最小发车间隔和最大发车间隔Hmin、Hmax分别设置为1、5 min。在研究时段内第1班抵达光电园站的换乘乘客步行至换乘公交站,用时以2 min计,接运公交最早抵达该接运公交站点的时间Tmin应为07:03。根据本地乘客到达率与换乘到达人数,得到接运公交可到达的班次及换乘人数。具体07:00—08:30时间段内接运需求见表3。

表3 886路公交车07:00—08:30时间段内接运需求

最长可容忍的排队长度Q设置为35名乘客。最长可容忍等待时间TL设置为8 min,参数α和β均为0.5。接运公交的规模J为20辆,满载时载客量为60名乘客,接运公交的运营成本参数为1.7。其中参数μ1通过重庆市城镇常住居民人均可支配收入进行换算,取0.36元/min:μ2通过平均等待候车超过Q后放弃的人数与重庆市人均工资进行换算,取1.17元/人;μ3通过选取电动公交购置成本、维修成本与使用寿命换算为每日每趟成本,取43.28元;根据电动公交的使用寿命确定其使用成本的年化系数φ=0.187 4;用公交车充电电价表示μ4,取0.82元/(kW·h)。

在蜂群算法中,食物源、雇佣蜂和观察蜂的数量均设定为90。最大迭代次数设为2 000。在MATLAB(R2016A)环境中进行数值测试,并且在具有英特尔核心I7-1165G7 CPU的电脑上执行所有计算。

4.1 最优解

建立MINLP模型并运用蜂群算法得到合适的接运电动公交到达时刻为07:07、07:15、07:20、07:25、07:30、07:34、07:39、07:43、07:47、07:50、07:54、07:58、08:03、08:07、08:11、08:16、08:21、08:25,共18班。由于轨道交通光电园站与公交886路在软件园渝兴广场站换乘,接运电动公交从始发站到达换乘站的距离为10.7 km,需要行驶约42 min,可得到这18班电动公交始发站的发车时刻,见表4。

表4 优化后的发车时间

该时刻表下的总成本为1 355.32元,其中总等待时间成本为298.17元,总转移失败成本为84.03元,电动公交总运营成本为867.40元,电动公交车充电成本为105.71元。

目前该线路早高峰采用均匀发车时刻进行发车,在研究时段内发车班次为18班,发车间隔为5 min,总成本为1 773.05元。与现有均匀时刻相比,采用该模型优化后的时刻表在总成本上降低了23.56%。

4.2 模型评价

为了进一步评价所提出方法的适用性,将其与遗传算法和粒子群算法进行比较。与ABC算法不同,遗传算法需要交叉和变异算子来生成新的解,交叉率和变异率分别为0.9和0.5。在粒子群算法中,每个粒子的位置就是一个潜在解,在ABC算法中,粒子的数量等于食物源的数量。将粒子群算法的惯性权值设置为0.7,学习因子1设置为2.0,学习因子2设置为2.0。与ABC算法类似,遗传算法和粒子群算法的最大迭代次数均被设置为2 000次,3种算法迭代曲线见图4。

图4 3种算法的收敛曲线Fig. 4 Convergence curves of three kinds of algorithms

3种算法在求解MINLP模型过程中均有较好的收敛性,其性能和优化结果见表5。3种算法中ABC算法得到的最优解优于遗传算法与粒子群算法得到的最优解,总成本分别为1 355.32、1 393.56、1 361.82元。由图4可知,收敛过程中粒子群算法很快达到收敛,并维持该收敛结果较长代数;人工蜂群算法收敛过程耗时较长,在算法迭代至800次左右时再次给出更优结果。

表5 3种算法的性能对比

5 结 语

在考虑公交公司运营成本的同时,充分考虑公交车容量限制与续航能力的约束,将乘客换乘等候与换乘失败两部分成本考虑在总成本内,能够更好地从乘客角度出发优化电动公交的调度。笔者提出的基于MINLP的电动公交时刻表优化模型以及求解算法,通过优化发车时间间隔降低总运营成本,求解过程相比遗传算法和粒子群算法在效率与质量上均更优。由于考虑的换乘需求是已知的,而实际的换乘需求受换乘距离、等待时间等因素的影响不断变化,后续应继续研究动态换乘需求的电动公交调度问题。