双等腰三角形模型及相关结论

等腰三角形是特殊的三角形，自身具有很多性质，而两个等腰三角形结合往往会有新的结论.下面就一起探究双等腰三角形模型及其相关结论.

模型构建

一、共底双等腰，可得角相等

“共底双等腰”是指两个等腰三角形的底边共线，且其中一个等腰三角形的顶点在另一个等腰三角形一腰所在的直线上.下面三种情况都是“共底双等腰”模型.

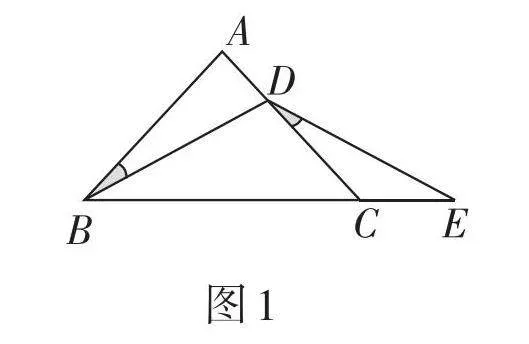
模型1：如图1，AB = AC，DB = DE，点D在线段AC上，则∠ABD = ∠CDE.

模型2：如图2，AB = AC，DB = DE，点D在CA的延长线上，则∠ABD = ∠EDC，∠BFE = ∠ADB.

模型3：如图3，AB = AC，DB = DE，点D在AC的延长线上，则∠ADF = ∠ABD，∠F = ∠BDC.

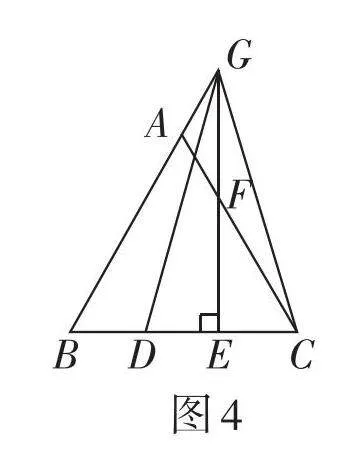
模型应用：如图4，△ABC为等边三角形，GD = GC，[S△GCD=2S△GBD]，AG = 3，求BG的长. （请同学们尝试求解，答案为 4）

二、双等腰手拉手，可得三角形全等

“双等腰手拉手”模型即“8”字形，具有双等腰、共顶点、顶角相等的特点.

模型：如图5，点C是等腰三角形ABC和等腰三角形CDE的公共顶点，AC = BC，CD = CE，∠ACB = ∠DCE，则△ACD ≌ △BCE.

模型变式：如图6，△ABC与△EDC都是等边三角形，当点B，C，D在一条直线上时，连接AD，BE交于点M，连接CM．

结论1：利用等边三角形的边、角的特殊性，该模型可以与旋转联系起来，得到全等三角形.

（1）△BCE绕着点C旋转到△ACD，结论为△ACD ≌ △BCE（SAS），AD = BE；

（2）△BCP绕着点C旋转到△ACQ，结论为△BCP ≌ △ACQ（ASA），CP = CQ；

（3）△PCE绕着点C旋转到△QCD，结论为△PCE ≌ △QCD（SAS），PE = QD.

结论2：得到新的特殊三角形，即△CPQ为等边三角形.

结论3：得到直线位置关系，PQ[⫽]BD，AC[⫽]DE，AB[⫽]CE.

结论4：证明三角形全等后，再利用“8”字型，可求出一些角的度数.例如：∠BMA = ∠EMD" = ∠BMC" = ∠CMD" = 60°.

结论5：证明三角形全等后，再利用等面积法，根据角平分线的判定定理可以得出MC平分∠BMD.

结论6：利用截长补短法可得到线段之间的关系，BM = AM + CM， DM = ME + MC.

模型应用：如图6，（1）求证：△ACD ≌ △BCE；（2）试探究线段BM与线段AM，CM之间的数量关系，并说明理由．（请同学们尝试证明）

分层作业

难度系数：★★★ 解题时间：3分钟

1.如图7，点C是线段AE上的一点，分别以AC，EC为边在直线AE的同侧作等边三角形ABC与等边三角形CDE，连接AD，BE分别交BC，CD于点F，G，AD与BE相交于点O，连接FG. 则下列结论中成立的有（ ）.

（1）AD = BE；

（2）∠AOB = 60°；

（3）△AFC ≌ △BFO；

（4）△CFG是等边三角形；

（5）DE = DF．

A. 2个 " B. 3个 C. 4个 D. 5个

难度系数：★★★★ 解题时间：10分钟

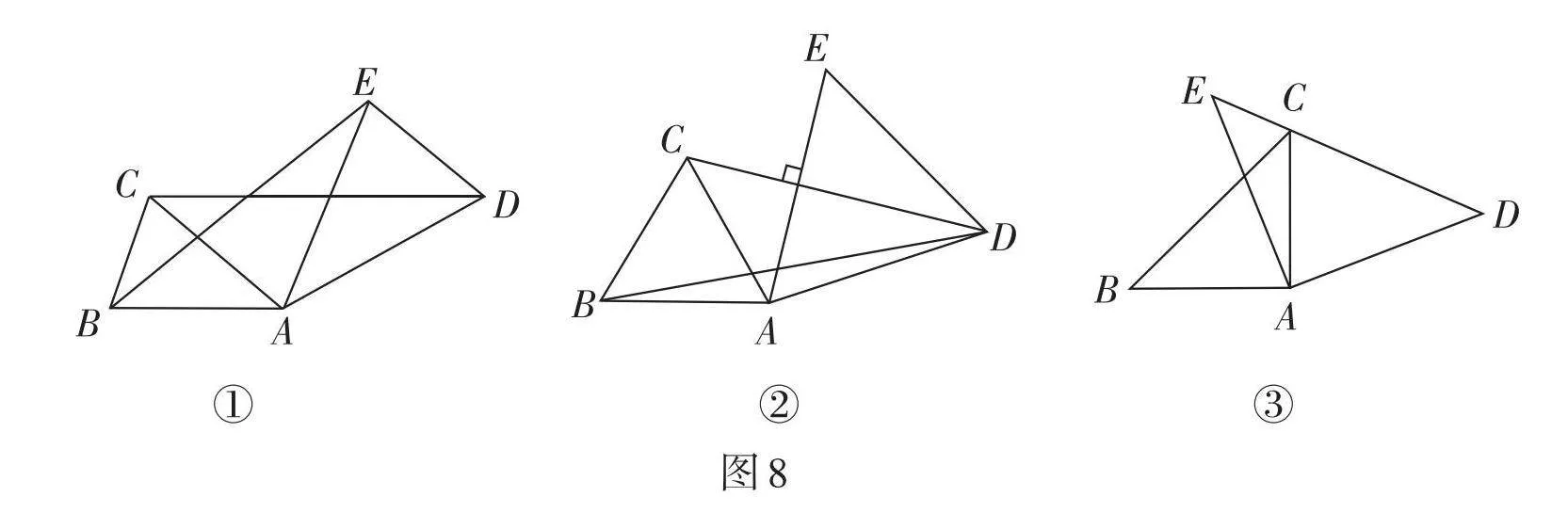
2.[△ABC]和[△ADE]都是等腰三角形，其中[AB=AC]，[AD=AE]，且[∠BAC=∠DAE]．

（1）如图8①，连接[BE]，[CD]，求证：[CD=BE].

（2）如图8②，连接[BD]，[CD]，若[∠BAC=∠DAE=60°]，[CD⊥AE]，[AD=3]，[CD=4]，求[BD]的长.

（3）如图8③，若[∠BAC=∠DAE=90°]，以点A为旋转中心旋转[△ABC]，使得点[C]恰好落在斜边[DE]上，试探究[CD2]，[CE2]，[BC2]之间的数量关系，并加以证明．

（答案见本页）

（作者单位：开原市民主教育集团里仁学校）