数学教学，谨防几种“失根”现象

摘 要：数学的价值不在模仿而在创新，数学的本质不是技能而是思想。学生需要的，不是复制别人的数学，而是建构自己的数学。数学教学，要谨防重方法、轻溯源，重指令、轻建构，重外显、轻内隐等“失根”现象。

关键词：小学数学；溯源；建构；内隐

南宋著名教育家朱熹在其《论知行》中有“事要知其所以然”之论。数学教学也需要引导学生“知其所以然”。然而我们发现，一些教师虽然有了这样的认识，可是在操作层面往往差了关键的一步。没有了这关键一步，就像丢失了数学教学的“根”。实践中，常见这样一些“失根”现象。

一、重方法，轻溯源

“溯源”意指追溯事物发生的根源。学生学习数学，获得必需的数学知识、掌握必要的方法当然是重要的，但不应是教学的全部。教师应该带领学生追寻数学知识的逻辑起点，透视知识背后所蕴含的数学思想与方法，把握知识的本源。

一位教师教学“用两把尺规范画平行线”时，在学生利用直尺的上下两条边、练习本上的格子等画出平行线后，就先让学生自学，然后在黑板上边示范画边强调步骤。结果，学生完成相关练习时错误率很高，特别是当已知直线变换方向或过直线外一点画已知直线的平行线时，许多学生不知道手上的尺子怎么摆放，还有些学生干脆用一把尺子直接“平移”画。

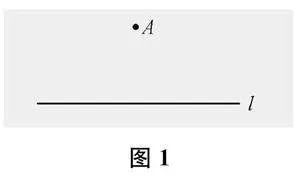
这样的教学，就忽略了引导学生对画法内在的本质进行探究。其实，当学生利用直尺的上下两条边和练习本上的格子等画出平行线后，教师可以加大难度，抛出问题：如下页图1所示，过直线外一点，你能画出已知直线的平行线吗？然后让学生分小组尝试完成。学生可能会用一把直尺直接画，也可能先用直尺与已知直线重合再“平移”至直线外一点处画。对此，教师追问：用一把直尺直接画出的直线一定与已知直线平行吗？直尺在向上平移的过程中晃动了没有？有什么办法能使直尺在平移的过程中不晃动？这样，就能促使学生自然地生发用两把直尺画平行线的需要，也能较好地避免机械模仿后快速遗忘的缺憾。

日常教学中，也有不少教师错误地认为，教材上诸如“画平行线”这些“规定性知识”，直接介绍或让学生自学是理所当然的教学方式。然而，很多“规定”都有其内在的因由，引领学生了解、体验、经历这些“规定”的来龙去脉，无疑能帮助学生主动建构“规定”，体验到“规定”的合理性与必然性，进而自觉应用“规定”解决相关问题。

二、重指令，轻建构

时下，小学数学课堂教学中不少教师都注重引领学生通过动手操作探究数学问题、获得数学结论、理解数学知识。但如果操作活动只是在操作，就会失去其应有的价值。建构主义教育理论告诉我们，教学并非机械的知识传递，而是对知识的有效转换与处理。教学过程中，教师必须关注学生如何理解外在现象，倾听学生对问题的内在看法，并以此为依据积极、正确地引导学生。

一位教师教学“9加几”时，在引导学生猜想9+4的得数是多少后，说道：“9＋4是不是等于13呢？老师在篮子里给每位小朋友准备了苹果圆片，同学们想不想试着自己去摆一摆、说一说？”学生操作后，教师组织交流分享：“谁愿意把你的想法与大家分享一下？说说你是怎样算的？”一位学生说：“我是这样数的：9、10、11、12、13。”一位学生说：“我直接口算出答案的，我在幼儿园就会了。”

表面上，学生似乎经历了探究的过程。但是，透过喧嚣与热闹的操作活动场景，用理智的眼光去审视，就可以看出：“摆一摆、说一说”时，学生仅仅是按照老师的指令在操作，学生并不知道为什么要这样做。所以，当教师请学生说说“这样折就发现了什么”时，连续两位学生的回答都令人茫然。

张奠宙先生说：数学教学的有效性，关键在于对数学本质的把握、揭示和体验。教师不但要使学生经历计算方法的探索过程，还要使他们懂得为什么要这样操作，才能真正体现操作活动的价值。我们更应注重引导学生经历加法的探究过程，体会“凑十法”的本质，注重引导学生数学化的表达，凸显数学思维过程。这样，学生的思维才能从无序走向有序，从具体走向抽象，从浅表走向深入，从感性走向理性。

教师可以紧扣关键问题，启发学生的数学思考。比如，在学生动手操作之前，将“同学们可以摆一摆、说一说”的指令式要求，改为思考性问题：“你想怎么验证？你为什么这样验证？ ”有效的问题引领，不仅能够激发学生的学习兴趣，还能启发学生的数学思考，达到设疑、激趣、启思的作用。

三、重外显，轻内隐

学生学习数学知识，就是将前人的经验转化为自己的经验的复杂过程。数学课程内容不仅包括数学的一些现成结果，还包括这些结果的形成过程。教学中，教师要多问学生：“你是怎么知道这个结果的？”而不能只是问学生：“这一题的答案是什么？”

一位教师教学《找规律》一课中的问题“照这样摆下去，左起第19盆是什么颜色的花？”时，在学生展示了计算方法和答案“19÷3=6（组）……1（盆），第19盆是蓝花”后，提问：这里的“19、3、6、1”各表示什么？在学生回答后，教师追问：余数是“1”，我们就看第几组的第几盆？当学生说出余1就看第1组的第1盆时，教师非常高兴地给予了表扬，并多次强调：余数是几，就看第1组的第几盆。虽然在接下去的练习中，大部分学生也能依葫芦画瓢地解决类似的问题，但笔者课后询问学生“为什么余下几就看第1组的第几盆”，不少学生支支吾吾，说不清楚。

看得出来，这位教师很满足于学生发现的“规律”，也觉得在他的几次强调下学生都掌握了这样的“规律”。事实上，大部分学生只是从形式上知道了怎样根据余数判断，并未领悟内在的道理。而“为什么余下几就看第1组的第几盆”的内在道理，才是本课的关键所在。对此，教师可以展开如下教学：

师

（出示图2）

你们能在书上圈圈、画画或在作业纸上用文字写一写，也可以用你们熟悉的符号代替画一画，表示出它的排列规律，然后再说一说吗？

生 它是按“蓝黄红蓝黄红蓝黄红”的顺序排列的。

师 你能否加上什么标记，让人一看就明白你找到的规律。

生 加括号就行：

（投影展示）

（蓝黄红）（蓝黄红）（蓝黄红）。

生 画横线也行：

（投影展示）

蓝黄红 蓝黄红 蓝黄红。

生

（投影展示：△□○ △□○ △□○）

△表示蓝花，□表示黄花，○表示红花，它是按“蓝黄红蓝黄红蓝黄红”的顺序一组一组排列的。

师 同学们明白他们的想法了吗？

（其他学生的想法基本相同，只不过表示方法不同，有的用“123123123”表示，有的用“abcabcabc”表示……）

师 我们一起来小结一下，请回答：每组有几盆花？每组花是按什么颜色顺序排列的？

生 每组有３盆花，按“蓝黄红”的顺序排列。

师 把这两个问题合在一起回答，就是它的排列规律。跟着老师说一遍：３盆一组，每组按“蓝花、黄花、红花”的顺序排列。

（学生跟读。）

师 以后，我们就用这样的表达方式来说事物排列的规律。按照规律，第19盆花会是什么颜色的？能用你的好方法在纸上快速把它找出来吗？

［学生有用数数的方法找到，有用文字书写排列找到，有用符号代替排列找到，更有用除法计算方法快速找到的。教师结合学生的回答在黑板上相机板书：19÷3=6（组）……1（盆）。］

师 你能说说算式中每个数的含义，以及为什么这样计算吗？

生 第１盆到第19盆花一共有19盆花，每３盆一组地分，19盆分成了6组还余１盆，余下的１盆也就是第19盆花，应该分在第7组的第１盆。每组的第１盆都是蓝花，第19盆就是蓝花。

……

总之，数学的价值不在模仿而在创新，数学的本质不是技能而是思想。学生需要的，不是复制别人的数学，而是建构自己的数学。当然，建构的经历意味着要面临很多困惑、挫折，甚至失败，但这些是学生生存、成长、发展、创造所必须经历的过程，也是数学教学的“根”。数学教学，要谨防“失根”现象！