电磁阀半主动悬架线性变参数μ综合鲁棒控制
寇发荣, 李盛霖, 杨旭东, 邢龙龙
(1.西安科技大学 电气与控制工程学院,西安 710054;2.西安科技大学 机械工程学院,西安 710054)
悬架系统是汽车的重要组成部分,对车辆平顺性和操纵稳定性具有重要的影响。半主动悬架因其具有成本低、能耗小和性能优良等优点成为研究的热点[1-5]。但由于不同类型的悬架具有不同的非线性特性且包含多种不确定性,悬架系统性能的好坏还取决于模型的精确度和控制策略的设计。
在实际的半主动悬架系统中存在复杂的非线性动力学和外界扰动等问题[6-8]。因此,除考虑舒适性以外,悬架系统还应具有良好的抗扰能力和鲁棒性。夏长高等[9]设计了一种内置电磁阀式阻尼连续可调减振器,对可调阻尼力进行理论分析,在Simulink 中建立电磁阀力学仿真模型;赵凯旋等[10]通过对电磁阀式阻尼可调减振器的力学特性研究,建立了减振器的AMESim模型;陈双等[11]根据电磁阀式减振器节流孔油液流动及开阀压力,分别推导电磁阀式阻尼可调减振器在伸张行程和压缩行程的阻尼力计算式,通过AMESim软件搭建减振器模型;寇发荣等[12]针对1/4车辆内置电磁阀式半主动悬架系统的非线性和簧载质量不确定性问题,设计了一种内置电磁阀式半主动悬架自适应反演控制算法;张亮修等[13]考虑1/4车辆阻尼连续可调(continuous damping control, CDC)半主动悬架系统的非线性约束条件,设计了一种混杂模型预测控制方法;陈龙[14]等人为提高汽车平顺性,针对新型阻尼连续可调减振器提出了一种多模式切换控制策略;Jeyasenthil等[15]针对四自由度磁流变悬架系统车辆簧载质量变化问题,提出了一种基于定量反馈理论的多变量控制器。目前,针对磁流变悬架[16-17]和半主动空气悬架[18],已建立许多较为经典的非线性模型,而在对电磁阀半悬架系统建模和控制器设计的过程中,大多研究在考虑半主动悬架系统的非线性时,是通过对物理模型的分析来建立理论上的液压模型。但减振器阀系复杂,建模困难,液压模型在实际反馈控制系统中难以实现。并且建模时只针对1/4车或半车系统,忽略了整车系统之间的耦合关系。理论上,所建立模型越精确,则控制系统的性能越好。此外,所采用的控制策略大多为线性单目标控制,忽略了多性能之间的冲突。当系统存在多种不确定性和外界扰动时,难以保证系统的鲁棒性。
考虑上述悬架系统特性和控制系统问题,本文以七自由度电磁阀式半主动悬架系统为研究对象,首先建立电磁阀减振器被动阻尼下的非线性阻尼力表达式,并考虑螺旋弹簧非线性力,采用线性变参数(linear parameter varying, LPV)技术近似电磁阀半主动悬架系统的高度非线性动力学,建立了一个七自由度LPV模型。其次,考虑悬架系统中多个参数变化、系统建模误差和外界干扰等因素,设计了一种基于输出反馈的LPV-μ综合鲁棒控制器。控制系统根据实时外部扰动和约束条件在性能目标之间进行权衡,同时实现鲁棒的振动控制。最后,进行系统鲁棒性、最坏情况下的抗扰能力和标准随机路面下的控制性能仿真分析,并进行硬件在环试验验证所提出方法的有效性。
1 七自由度半主动悬架系统建模
1.1 电磁阀减振器非线性力学模型
电磁阀半主动悬架系统的核心部件为阻尼连续可调减振器,本文采用的是外置式电磁阀减振器。在实际控制系统中,控制器通过实时接收传感器所采集的信号来输出理想控制力。所得到的理想控制力再输入减振器逆模型求解出所需的理想电流值,然后通过驱动器在一定范围内输出实际电流值来实时控制电磁阀的开度,调节阻尼力的大小。当输入电流越大时,其阻尼力越小。
通过搭建如图1所示的1/4电磁阀半主动悬架试验平台进行台架试验,测得电磁阀减振器无电流输入时被动工况下的非线性阻尼特性,并建立非线性阻尼力的数学表达如式所示
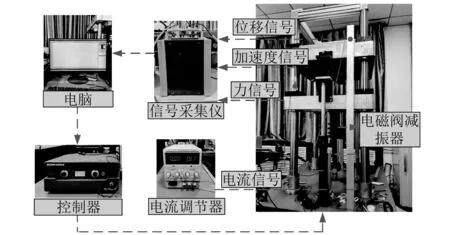
图1 电磁阀减振器阻尼力特性试验平台Fig.1 Damping force test platform of solenoid valve damper
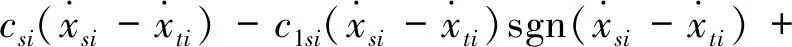
(1)
式中:csi为线性阻尼系数;c1si和c2si为非线性阻尼系数;c3si和c4si为相对速度和相对位移相关系数;c5si和c6si为速度相关范围内非线性阻尼调整系数,在被动工况下建模时c6si=0。
将所建立的非线性阻尼力与试验数据相比较,其结果如图2所示,所建立的非线性力数学表达式能近似表达电磁阀减振器被动工况时在整个速度变化范围内的非线性特性。根据阻尼特性试验,确定非线性阻尼力模型在0电流输入下的各个参数分别为
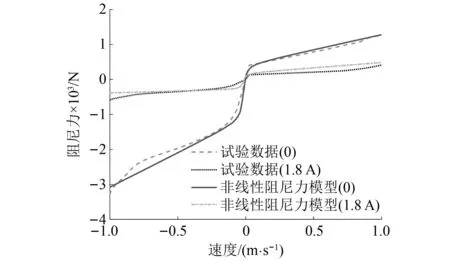
图2 非线性阻尼力模型和不同电流输入时的实际阻尼力Fig.2 Nonlinear damping force model and actual damping force at different current inputs
c1si=550,c2si=500,c3si=70,
c4si=50,c5si=350,c6si=0
在1.8 A电流输入下的各个参数分别为
c1si=-100,c2si=150,c3si=70,
c4si=50,c5si=50,c6si=-1 200
螺旋弹簧非线性力可以表达为
Fksi=ksi(xsi-xti)-k1st(xsi-xti)3
(2)
式中,k1si为螺旋弹簧非线性刚度系数。
1.2 七自由度悬架系统非线性LPV模型
为了对整车七自由度电磁阀式半主动悬架系统进行分析,需要进行适当简化,其简化模型如图3所示。
当车辆俯仰角和侧倾角较小时,1/4悬架处车身位移可通过泰勒展开线性近似为
xs1=xsc+Lfθ+Lwφ
xs2=xsc+Lfθ-Lwφ
xs3=xsc-Lrθ+Lwφ
xs4=xsc-Lrθ-Lwφ
(3)
式中:xs1,xs2,xs3和xs4分别为车辆左前、右前、左后和右后处车身垂向位移;xsc为车身质心处垂直位移;θ为俯仰角;φ为侧倾角;Lf为车身质心到前轴的距离;Lf为车身质心到后轴的距离;Lw为左右车轮间的距离。
根据牛顿第二定律,可建立七自由度电磁阀半主动悬架系统非线性动力模型为
(4)
(5)
(6)
(7)
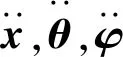
根据式(1)和式(2)中的非线性项,可选取八个包含非线性依赖的调度变量来构建整车电磁阀半主动悬架系统的LPV增广模型,通过构建LPV模型可使线性化系统与非线性模型完全相同。所选取调度变量分别为悬架相对位移ρksi和悬架相对速度ρcsi。在实际控制中,悬架相对位移可由位移传感器测量,而相对速度则可通过相对位移的数值微分来获得。调度变量的表达式为
(8)
ρksi=(xsi-xti)2
(9)
则非线性阻尼力和弹簧力可表示为如下参数依赖的形式
(10)
Fksi=ksi(xsi-xti)-ρksik1si(xsi-xti)
(11)
式(10)中非线性阻尼力的第一项和第二项为线性部分,第三项和第四项为非线性部分。当构建LPV状态空间模型时,需要将该非线性项放入扰动矩阵中,作为一项扰动输入。设该非线性扰动为
(12)
d2i=c5si
(13)
在对整车非线性系统进行LPV线性近似的时候,会导致线性系统的状态空间模型中有一系列的参数依赖。从理论分析的角度,调度变量和不确定性的作用相同。因此,可对整车LPV系统的参数依赖项用线性分式变换(linear fractional transformation, LFT)形式表示,将参数依赖项从被控系统中分离出来。
被控系统P的参数依赖项可由如式(14)所示的对角结构来表示,该结构具有输入信号qρ和输出信号υρ。可通过LFT互联结构来表示系统输入与输出的反馈关系为
Δρ=diag([ρcsiρksi])
(14)
(15)
根据上述对七自由度车辆电磁阀半主动悬架系统特性分析,整车LPV形式的电磁阀半主动悬架系统状态空间增广模型可表示为
(16)
式中,ρ为调度变量。
(17)
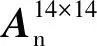
1.3 系统不确定性分析与建模
根据车辆参数对悬架系统动态特性的影响,将簧载质量、线性弹簧刚度、轮胎刚度和线性阻尼系数作为摄动参数。参照文献[19-20],根据汽车乘客上下车重量变化,假定簧载质量msc的不确定度为20%;由于所用弹簧为变径弹簧,弹簧刚度在车辆行驶过程中为非固定值,假定弹簧刚度ksi的不确定度为15%;考虑汽车在行驶过程中胎压的变化,假定轮胎刚度kti的不确定度为15%;此外,减振器油液会受温度变化、摩擦以及精度问题等影响,假定阻尼系数csi的不确定度为15%。
(18)
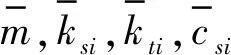
根据半主动悬架系统的动力学微分方程可知,质量msc需作为分母,其他的不确定性参数则作为分子。对以上不确定性参数进行下线性分式变换(low linear fractional transformation, LLFT)为
(19)
(20)
通过LLFT方法将参数标称值和不确定性部分分离,定义参数虚拟对角结构为Mup,不确定性虚拟对角结构Δup,不确定参数虚拟输入矢量yup和不确定参数虚拟输出矢量uup。
除系统参数摄动外,系统建模和实际模型通常还存在非结构化的误差,这里采用乘法不确定性来描述模型的建模误差。设P为被控系统的传递函数模型,则含有乘法不确定性的被控系统的模型可以表达为
Pum(s)=[1+Δum(s)Wum(s)]P(s), ‖Δum(s)‖∞≤1
(21)
式中:Δum为非结构化未知有界摄动;Wum为未知摄动的加权函数,反映了不同频率下建模误差大小。
2 LPV-μ综合控制器的设计与分析
2.1 加权函数的设计
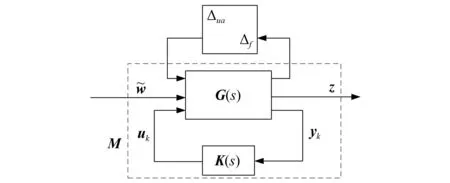
在第1章对非线性和不确定性分析与建模的基础上,可以得到如图4所示七自由度电磁阀半主动悬架系统闭环互联结构,P为式(16)所示的包含参数不确定性的LPV增广模型,K是基于μ综合的控制器。
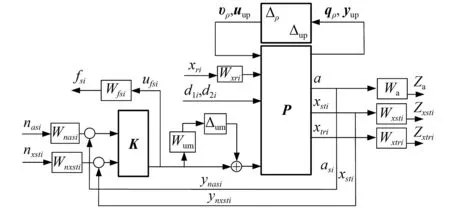
图4 整车半主动悬架系统闭环互联结构Fig.4 Closed-loop interconnection structure of semi-active suspension system for the full vehicle
在进行控制器设计之前,首先需要根据系统性能目标、外部影响和约束条件等选择适当的加权函数。在鲁棒控制器设计的过程中,加权函数的选取至关重要,很大程度上决定了控制系统性能的好坏。控制系统中各个部分加权函数的作用各不相同,根据外部扰动的影响,路面激励的加权函数设置为Wxri=0.1,即假定路面干扰最大幅值不超过0.1 m。考虑传感器测量噪声的影响,选择加速度传感器和位移传感器噪声加权函数分别为Wnasi=0.001和Wxsti=0.001,即传感器在整个频域内的噪声均假设为0.001。建模误差通过系统输入端的乘法不确定性来模拟,作为一种未建模动态,设置其加权函数为Wum=(s+100)/(s+1000),意味着在低频时建模误差约为10%,高频时建模误差达到100%。
设置车身加速度性能输出加权函数的目的是在理想频域内,使得车辆的车身振动降低,提高汽车的平顺性。根据性能目标,设置Wa为车身加速度的加权函数,包含了车身垂向加速度加权函数Wasc,俯仰角加速度加权函数Waθ和侧倾角加速度加权函数Waφ。悬架动挠度加权函数Wxsti和轮胎动载荷加权函数Wxtri的目的则是使车辆的悬架动挠度和轮胎动载荷尽可能小。本文不侧重轮胎动载荷的设计,所以其加权函数设置为Wxtri=1。通过频域设计的方法,确定车身加速度和悬架动挠度性能输出的加权函数为
Wasc=0.001((600s+1)/(0.002 5s+600))
Waθ=0.002((600s+1)/(0.0025s+600))
Waφ=0.002((600s+1)/(0.0025s+600))
(22)
Wxsti=(s+100)/(100s+0.05)
(23)
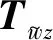
实际悬架系统的工作空间有限,悬架挠度有一定的工作范围,为了避免减振器超过最大行程撞击限位块,保证其使用寿命和安全性,悬架动行程约束可表达为如式(24)所示。为避免系统控制力输入过大和执行器输出饱和,可通过理想力输出加权函数Wfsi来约束系统控制力的输入。在控制器设计中理想控制力的加权函数选取为Wfsi=0.002 5,理想力约束如式(25)所示。
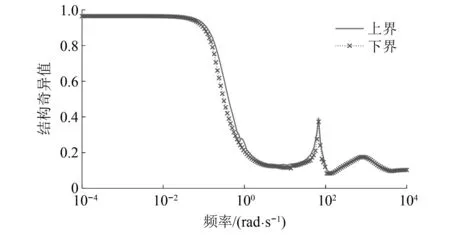
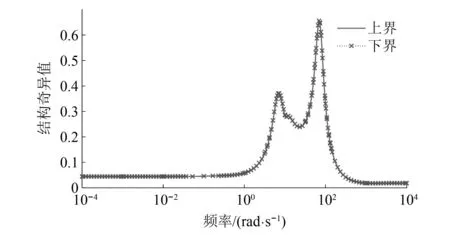
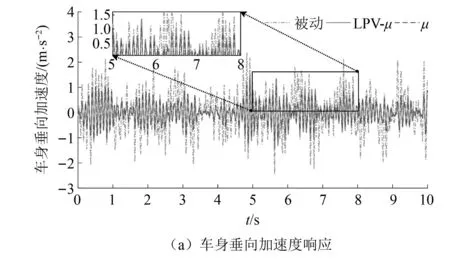
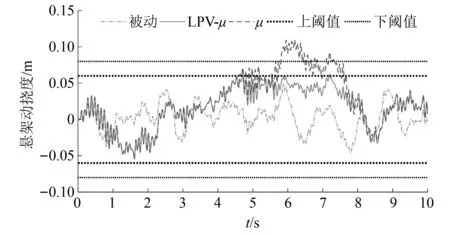
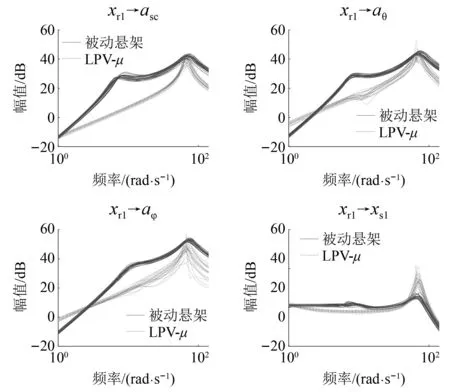
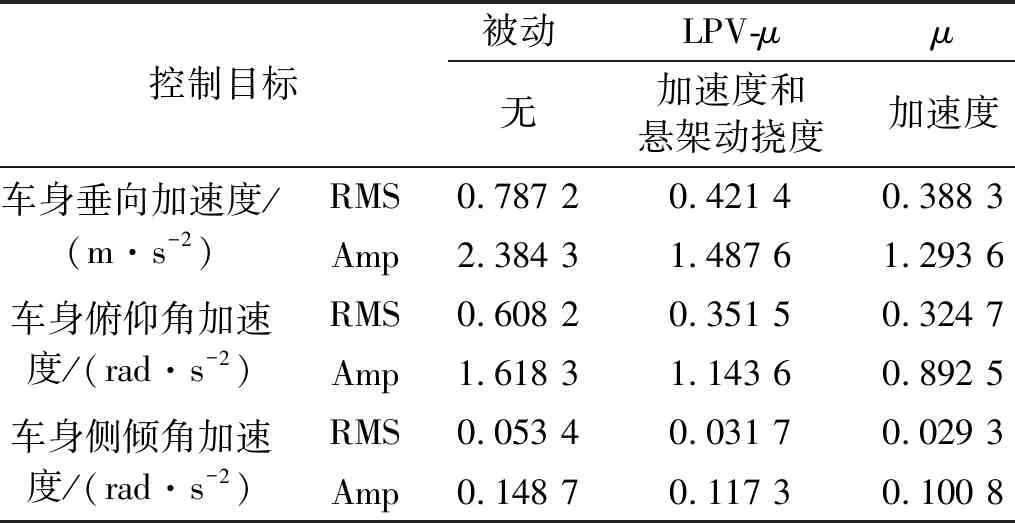
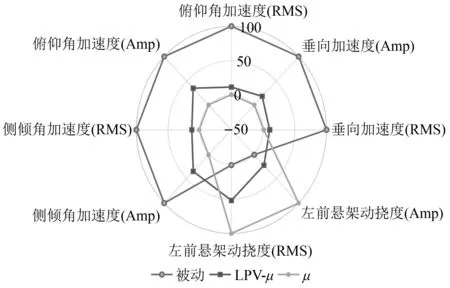
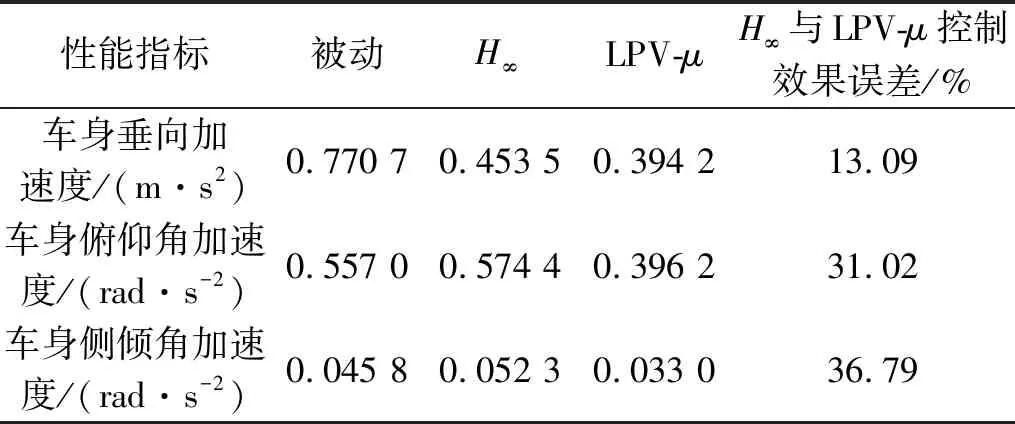
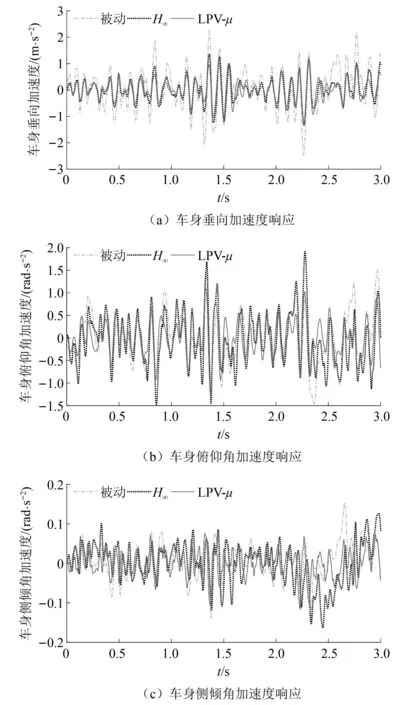
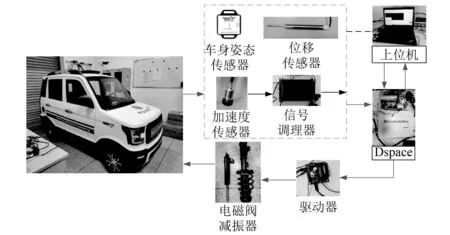
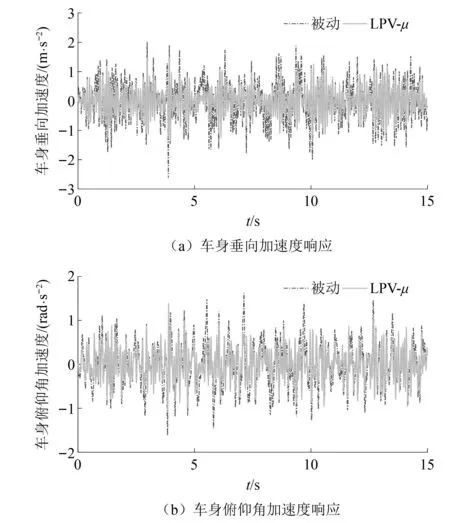
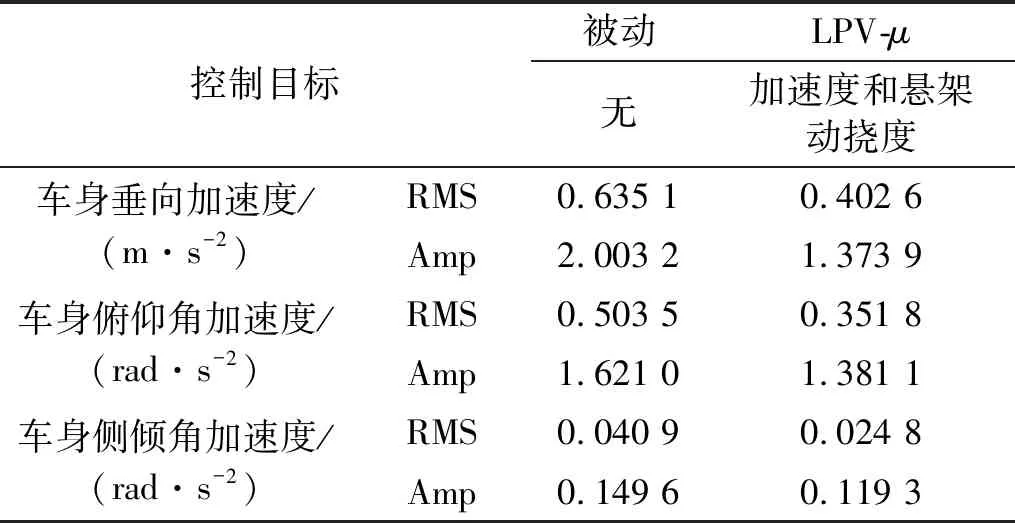
|xsti| (24) fsi,min (25) 式中:xsti为实际悬架动挠度;xsti, max为悬架动挠度的最大值。 考虑上述约束条件,对性能输出中车身加速度和悬架动挠度的加权函数分别给予参数依赖的增益λa(ηx)和λst(ηx),来体现对不同性能指标的侧重。 Wasc(ηx)=λa(ηx)/Wasc (26) Waφ(ηx)=λa(ηx)/Waφ (27) 式中:λa(ηx)为车身加速度的变参数加权增益;λst(ηx)为悬架动挠度的变参数加权增益;ηx为整车各个悬架车身与车轮之间相对位移总和的平均值。 为避免加权函数值为0而导致控制器失效,将最大增益设置为λmax=0.99,最小增益设置为λmin=0.01。根据电磁阀减振器的行程变化范围,将悬架动挠度判断阈值的上限值η1和下限值η2分别设置为极限值的0.6倍和0.8倍,即: (28) 车身加速度和悬架动挠度的变参数增益分别如式(29)和式(30)所示。 (29) λst(ηx)=1-λa(ηx) (30) 式(29)和式(30)表明,当整车悬架动挠度均在极限值的0.6倍以下时,控制目标仅是提高汽车平顺性。当其中一个或多个悬架动挠度超过极限值的0.6倍时,控制目标开始侧重悬架挠度的设计。悬架动挠度越大,其加权增益越大,车身加速度加权增益越小。当其中一个或多个悬架动挠度超过极限值的0.8倍时,控制目标为降低悬架动挠度,此时几乎不考虑汽车舒适性,车身加速度加权增益最小。归一化后LPV形式的性能目标加权增益变化如图5所示。 图5 控制系统性能指标参数依赖增益变化图Fig.5 Parameter-dependent gain variation of the control system performance index 鲁棒μ综合控制器的设计,是将反馈控制系统结构奇异值μΔ(M)的上界与H∞控制器结合的一种综合设计方法。其目的是通过求解一个具有鲁棒稳定性和鲁棒性能的解,来降低在含有不确定性下外部扰动对系统性能的影响。为对图4所示的半主动悬架闭环互联系统进行LPV-μ综合控制器的设计,针对非线性参数依赖模块Δρ、参数不确定性模块Δup和非结构化建模误差模块Δum,定义混合不确定性对角模块为 (31) 在不确定性模块中引入虚拟性能不确定块Δf={Δf:‖Δf‖∞≤ 1}来表示μ综合框架中的性能需求,则增广的不确定性结构Δ为 (32) 将整车含有混合不确定性的反馈系统表达为μ分析的一般综合框架形式,其结构如图6所示。 图6 整车系统μ分析与设计的一般综合结构Fig.6 General synthesis structure of μ analysis and design for the full vehicle system 对系统G(s)和控制器K(s)进行下线性分式变换为 (33) 从输入到输出对所有不确定性的传递函数可以表示为 (34) 可通过结构奇异值来评估系统的鲁棒稳定性和鲁棒性能。根据结构奇异值理论[21],对于不确定性Δ,用最大结构奇异值μ(M(s))来表示 (35) 基于μ综合的控制器设计,目的是找到一个稳定的控制器K,使得结构奇异值满足如下条件 (36) 结构奇异值没有直接的方法来求得,需要引入最小相位矩阵和标度矩阵D,通过标定和使用无穷范数来获得。μ综合的问题可进一步转化为 (37) 选择稳定的D(s),然后进行D-K迭代,反复求解D和K,直到达到最佳性能,即可解决综合问题并找到满足性能要求和约束条件的最优化稳定控制器K。对于具有混合不确定性的系统,需采用D-G-K迭代来提升控制器性能,但所求解的控制器相对D-K迭代会更为复杂和更高阶。可通过模型降阶技术来获得一个保证性能要求且低阶的控制器。在控制器设计中,被控对象为LPV形式的状态空间模型。经过迭代计算,可求解出与ρ相关且满足系统性能要求的最优化非线性控制器K(ρ)。 此外,当闭环反馈系统存在摄动时,这些摄动会极大影响系统控制性能,甚至使得闭环系统稳定性和性能无法满足要求。需要对其鲁棒稳定性和鲁棒性能进行分析,分析其在给定摄动下,系统是否稳定和最坏情况下控制系统的性能。为了实现闭环控制系统的鲁棒稳定性,对于所有扰动应满足如下条件 (38) 如果要保证控制系统的鲁棒性能,则对于所有扰动应满足如下条件 (39) 在实际悬架系统中,总是存在参数摄动和非线性的影响,同时还包含一些非结构化的建模误差。对于包含这些不确定性所设计的LPV-μ综合控制器需要满足控制系统稳定性要求并保证性能需求。其鲁棒稳定性和鲁棒性能的结构奇异值频率响应分别如图7和图8所示。 图7 LPV-μ综合控制器鲁棒稳定性分析Fig.7 Robust stability analysis of LPV-μ synthesis controller 图8 LPV-μ综合控制器鲁棒性能分析Fig.8 Robust performance analysis of LPV-μ synthesis controller 由图7可知,在整个相关频域范围内,最大结构奇异值μ(0.965) <1。说明对于所有稳定的不确定性因素,闭环系统可以保证鲁棒稳定性,意味着系统在所设定的不确定度变化范围内,对所有值都可以保持稳定性。 要实现闭环控制系统的鲁棒性能,经过迭代计算后同样需要保证系统μ的值小于1。如图8所示,在LPV-μ综合控制下,结构奇异值μ的最大实现值为0.656,说明控制系统能保证良好的鲁棒性能。对于所有的干扰和噪声输入,能确保良好的振动衰减和扰动抑制能力。 为了验证所设计LPV系统模型和LPV-μ综合控制器的有效性,通过构建整车随机路面激励模型,对整车控制系统标称情况下的性能进行仿真分析。同时还设计了整车线性标称系统下的H∞控制器,与LPV-μ综合控制器对比分析在随机路面干扰输入下系统最坏情况时的性能,验证所设计控制系统的鲁棒性和抗扰能力。车辆系统参数及其不确定性如表1所示。 表1 车辆参数和不确定度 在仿真分析中,需要建立时域下整车随机路面激励模型。首先采用滤波白噪声法来建立二自由度随机路面激励模型。再通过前后轮之间的延时关系分析和左右轮之间的相干性分析。可构建以滤波白噪声作为输入,四轮路面激励作为输出的七自由度增广状态空间随机路面模型。 悬架控制系统性能仿真分析时,采用标准C级随机路面,仿真时车速为36 km/h,仿真时间为10 s。以车身垂向加速度asc,俯仰角加速度aθ,侧倾角加速度aφ和悬架动挠度xsti作为系统性能评价指标。不同控制下时域响应曲线如图9所示,悬架动挠度时域变化如图10所示,在不确定性情况下从左前轮路面输入到悬架车身加速度和左前悬架动挠度输出的频域响应如图11所示。 图9 不同控制下车身加速度时域响应Fig.9 Time domain response of body acceleration under different controls 图10 不同控制下悬架动挠度时域变化图Fig.10 Time domain variation of suspension dynamic deflection under different controls 图11 左前轮路面输入到悬架性能输出频域响应Fig.11 Frequency domain response of left front wheel road input to suspension performance output 采用不同控制方式时悬架性能响应的均方根(root mean square, RMS)值和幅值(amplitude, Amp)如表2所示。 表2 不同控制下悬架系统性能时域RMS值和Amp值 汽车平顺性主要通过乘客主观舒适性感觉来评价。根据国际标准,主要考虑支撑面x、y、z三个轴向。而这三个轴向的频率加权函数最敏感的频率范围为0~12.5 Hz,对人体影响最大的频率范围为4~8 Hz。 由图9和表2可知,在μ综合和LPV-μ综合两种控制下的悬架加速度性能均优于被动悬架,可以改善系统的性能。相比被动悬架,μ综合控制下的加速度RMS值分别降低了50.67%、46.61%和45.07%,此时车身加速度加权增益最大,悬架挠度加权增益最小。从图10悬架挠度的变化可知,虽然μ综合控制器控制效果最好,但未侧重悬架动挠度的设计。在0~5 s内,当悬架行程变化小于0.06 m的时候,控制系统目标仅为最小化车身加速度;在5~8 s内,当受到较大路面冲击时,电磁阀减振器的悬架行程会超过阈值上限0.08 m,接近甚至达到极限值。相比被动悬架,严重影响了汽车操纵稳定性和减振器寿命。 然而采用LPV-μ综合控制器,不仅能提高乘坐舒适性,还可缓和不同优化目标之间的冲突。在0~5 s和8~10 s内,此时路面冲击较小,悬架行程变化小于0.06 m时,可最大程度降低车身加速度。在第5 s,当悬架动挠度超过阈值下限0.06 m时,控制目标开始侧重于悬架动挠度;在第5.5 s,当悬架动挠度超过阈值上限0.08 m时,控制系统目标仅使悬架挠度最小。相比被动悬架,在LPV-μ综合控制下,车身垂向、俯仰角和侧倾角加速度RMS值分别降低了46.47%,42.22%和50.68%,并保证悬架行程变化范围不会超过所设置的最大阈值,始终保持在安全范围内。在保证汽车操纵稳定性的同时,可兼顾乘坐舒适性,验证了所设计LPV-μ综合控制器的有效性和可行性。 从图11所示的悬架性能频域响应可以看出,LPV-μ综合控制在所有不确定性下,在低频范围内均能有效降低车身垂向、俯仰角和侧倾角加速度的幅值,衰减路面扰动到车身的振动,提高乘坐的舒适性。 悬架性能RMS值和Amp值雷达图如图12所示,因性能指标量纲不同,将悬架各性能的RMS值和Amp值归一化到[1,100]范围内进行对比分析。 图12 不同控制下悬架性能RMS雷达图Fig.12 suspension performance RMS radar map under different controls 由图12可知,不同控制下悬架性能均方根值和幅值雷达图可以清晰地看出,μ综合控制器完全侧重于汽车行驶过程中舒适性能的提高,这种控制方法不考虑悬架动挠度的设计,路面冲击较大时悬架动挠度较大;而LPV-μ综合控制器在保证舒适性的前提下,可根据悬架实际状况在性能之间进行权衡,证明了所设计的模型和LPV-μ综合控制器在提高舒适性和多目标平衡方面的有效性和可行性。 为了评估所设计LPV-μ综合控制器的抗扰能力,对LPV-μ综合与H∞两种控制器在最坏情况下的闭环控制系统性能进行对比分析。通过计算出被控系统中所有不确定性在最坏情况下的值,分析在随机路面激励下系统最坏情况时两种控制器的控制效果。在3 s内两种控制下车身加速度性能输出响应结果如图13所示,加速度RMS值如表3所示。 表3 系统在最坏情況下LPV-μ综合与H∞控制的车身加速度响应RMS值 图13 系统在最坏情况下LPV-μ综合与H∞控制的车身加速度性能响应Fig.13 Body acceleration performance response of the system under LPV-μ synthesis and H∞ control in the worst case 图13和表3表明,当系统工作在最坏情况下时,LPV-μ综合控制与线性标称系统下所设计的H∞控制相比,车身垂向、俯仰角和侧倾角加速度RMS值分别降低13.09%、31.02%和36.79%,LPV-μ综合控制器的控制效果明显优于H∞控制器,且能保证一定控制性能。而系统最坏情况时H∞控制下部分车身加速度RMS值大于被动悬架,控制系统会失效。说明基于LPV七自由度悬架系统模型所设计的LPV-μ综合控制器的抗扰能力优于线性标称系统下所设计的H∞控制器,控制系统具有较好的鲁棒性。 为了验证所建立的模型和控制策略的有效性,进行整车电磁阀半主动悬架系统硬件在环测试。试验装置和设备如图14所示。 图14 整车电磁阀半主动悬架试验平台Fig.14 solenoid valve semi-active suspension test platform of vehicle 在整车硬件在环试验中,使用四个IEPE压电式加速度传感器来测量四轮处簧载质量加速度,通过IEPE信号调理器将加速度传感器信号转换为±10 V内的电压信号;使用四个差动位移传感器来测量簧载与非簧载之间电磁阀减振器的相对位移;使用一个六轴的车身姿态传感器来测量车身加速度;一个半实物仿真系统(Dspace)作为整车的ECU,接收所有传感器信号并进行信号处理,再通过控制系统计算理想控制力,并转化为实际占空比信号;两个驱动器产生0~2 A内的实际电流。 根据电磁阀减振器0~2 A内的阻尼试验数据,构建减振器BP神经网络逆模型来输出理想电流值。试验时采用LPV-μ综合控制策略,在随机不平路面下测试该方法的有效性,最终选取15 s内的试验数据。在不同控制下的悬架性能时域响应如图15和16所示。 图15 不同控制下车加速度时域响应Fig.15 Time domain response of acceleration under different controls 在整车硬件在环试验中,车身垂向、俯仰角和侧倾角加速度15 s内的RMS值和Amp值如表4所示。 表4 试验中不同控制下悬架系统性能时域RMS值和Amp值 根据试验结果图15、图16和表4可知,相比被动悬架,LPV-μ综合控制下车身垂向加速度、俯仰角加速度和侧倾角加速度RMS值分别降低了36.6%、30.14%和39.47%,可有效衰减路面扰动到车身的振动,提高乘坐舒适性。并且在LPV-μ综合控制下,悬架动挠度的最大值为0.051 m,最小值为-0.059 m,使得悬架行程变化不超过所设定的阈值下限0.06 m,保证了操纵稳定性,有效缓解性能目标之间的冲突,进一步验证了所设计模型和控制器的有效性。 图16 悬架动挠度时域响应Fig.16 Time domain response of suspension dynamic deflection (1)针对电磁阀式半主动悬架系统,建立整车LPV电磁阀半主动悬架非线性模型,并利用LPV技术线性近似电磁阀半主动悬架系统的非线性动力学,能充分地描述系统的非线性行为,通过仿真和试验验证了该模型的有效性。 (2)在对整车悬架系统非线性和不确定性分析的基础上,根据控制系统性能目标和约束条件,设计了一种LPV-μ综合鲁棒控制器,可根据不同条件在悬架多目标性能控制中进行权衡,并改善汽车平顺性。 (3)对系统鲁棒性能以及标称情况和最坏情况下的控制系统性能进行仿真分析,结果表明在LPV-μ综合控制下车身垂向加速度改善效果为46.47%,俯仰角加速度改善效果为46.47%,侧倾角加速度改善效果为50.68%,并在路面粗糙度较大时保证悬架行程变化范围不会超过所设定的阈值0.06 m。此外,在系统最坏情况下能有效保证控制系统的抗扰能力。最后开展整车电磁阀实车试验,分析了LPV-μ综合控制策略的控制效果,证明了该方法能够有效处理复杂的非线性动力学、外部扰动、系统不确定性和传感器噪声等问题。
Waθ(ηx)=λa(ηx)/Waθ
Wxsti(ηx)=λst(ηx)/Wxsti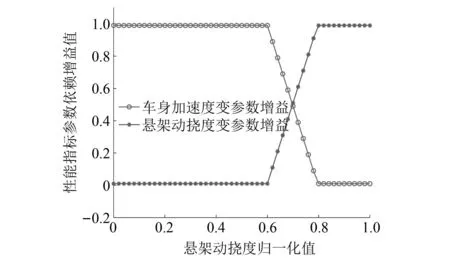
2.2 控制器设计与分析
3 控制系统性能仿真分析
3.1 标准随机路面下性能分析

3.2 最坏情况下性能分析
4 试验验证

5 结 论

