变滞回性能阻尼器的抗震性能及其在RC排架墩中的应用

董慧慧, 李艳玲, 韩 强, 杜修力

(北京工业大学 城市与工程安全减灾教育部重点实验室,北京 100124)

桥梁工程是交通生命线工程中的重要组成部分。一旦发生地震灾害,桥梁结构受到破坏或倒塌,以致切断震区的对外交通,将会给震后的救灾工作造成巨大困难,加重次生灾害,导致直接或间接经济损失巨大[1]。因此,提高桥梁结构抗震性能一直以来都是研究的热点问题。

为了提高桥梁结构的抗震性能,国内外学者提出了各种消能减震装置如耗能阻尼器等,将其装设于桥梁结构[2]。目前实际应用于桥梁结构的耗能装置多为金属屈服阻尼器、摩擦阻尼器和黏滞阻尼器[3-6]。石岩等[7]基于结构“保险丝”概念,在桥墩上附加防屈曲支撑(buckling restrained braces, BRB),研究结果表明,附加的“保险丝”构件可有效减小桥墩的地震损伤,增加耗能并起到保护作用。周海俊等[8]采用摩擦阻尼器有效地降低了斜拉桥桥塔的地震响应。Guo等[9]将黏滞阻尼器用于悬索桥减震研究,郑一峰等[10]在斜拉桥主梁与墩柱间设置黏滞阻尼器,显著地减小了梁端位移。附加耗能阻尼器的减震方式可以有效降低桥梁结构地震响应,但传统耗能阻尼器在强震后可能留有较大的残余变形,进而显著降低桥梁结构的抗余震能力及震后通行能力,大大增加了震后结构修复和维护的成本[11]。

目前有学者提出采用自复位技术减小结构的残余变形,在震后可快速恢复结构的使用功能。自复位结构属于可恢复功能结构(resilient structures, RS)[12],自复位结构最显著的特征在于震后的残余变形较小甚至为零[13]。近年来,国内外学者对自复位结构体系重要组成部分——自复位耗能阻尼器开展了一系列研究,并将其应用于桥梁结构[14]。Christopoulos等[15]最先提出采用预应力技术为自复位耗能阻尼器提供恢复力,并研发了利用高强预应力筋提供自恢复力的新型自复位摩擦耗能支撑。目前常用于自复位耗能阻尼器预应力系统的材料包括预应力筋、预压弹簧、预压碟簧等[16-18]。徐龙河等[19]采用基于预压碟簧提供恢复力的自复位耗能阻尼器,使斜拉桥桥塔主梁处的残余位移减小60%以上。基于已有的研究结果可知,现有的自复位阻尼器均能有效减小结构的残余变形。

目前,如何提高自复位阻尼器的自复位效果已成为近年研究重点[20]。自复位材料是影响自复位耗能支撑消除残余变形的重要因素之一。形状记忆合金(shape memory alloy, SMA)是一种具有超弹性效应的新型功能材料,利用SMA研发的阻尼器具有较大变形能力,同时无需预应力即可以获得较好的自恢复力[21],因此受到了自复位结构研究领域的密切关注。例如,Qiu等[22]加工SMA棒材制成SMA螺栓为SMA滑动摩擦阻尼器提供自复位力。Zhang等[23]基于SMA丝束研发了新型自复位阻尼器并将其用于RC框架结构,显著降低了层间残余位移率。已有研究结果表明,采用SMA的阻尼器可以有效减小结构残余变形,实现结构自复位功能,提高结构的抗震性能。

最近,Dong等[24]通过动力时程分析及易损性分析对附加具有相同屈服位移和屈服强度的自复位耗能阻尼器与纯耗能阻尼器的桥梁结构抗震性能开展研究。结果表明,PGA较小时,附加纯耗能阻尼器的结构峰值位移明显小于附加自复位耗能阻尼器结构,残余位移则略大于附加自复位耗能阻尼器结构的残余位移,易损性分析结果显示附加纯耗能阻尼器结构的失效概率小于附加自复位耗能阻尼器结构的失效概率;随着PGA增加,附加纯耗能阻尼器的结构峰值位移仍明显小于附加自复位耗能阻尼器结构,但残余位移明显大于附加自复位耗能阻尼器结构的残余位移,易损性分析结果表明附加纯耗能阻尼器结构的失效概率明显大于附加自复位耗能阻尼器结构的失效概率。由此可以发现,滞回性能单一的阻尼器难以满足不同强度地震作用下结构的抗震需求,即结构在不同地震水准下所需阻尼器的性能不同。

基于上述研究,本文提出一种基于SMA板环的变滞回性能阻尼器(variable hysteresis performance damper based on shape memory alloy,SMA-VHD),用以分级设防保护主体结构并减小传统耗能阻尼器在大震作用下的残余变形,通过理论分析结合数值模拟揭示其变滞回机理并研究其滞回性能,进一步将其应用于RC排架墩中研究其分级抗震的性能。

1 分级设防理念

我国当前抗震设计规范基于三水准设防目标[25],即“小震不坏、中震可修、大震不倒”。由于可恢复功能结构体系具有比传统抗震结构更高的抗震性能,其抗震设计应符合与震后功能可恢复性相关的抗震设防目标,不仅能够在地震中保护人们的生命财产安全,在地震后也能快速恢复其正常使用功能。周颖等[26]提出了为满足“小震及中震不坏,大震可修复、可更换,巨震不倒塌”的可恢复功能结构的四水准抗震设防目标,并对各级地震水准下的结构抗震性能目标进行重新定义。对应不同设防目标,结构在不同地震水准下震后使用要求及损伤状态有明确的分级规定,可恢复功能结构的分级抗震理念得以发展。

为了实现结构的分级抗震设计理念,具有分级设防功能的阻尼器应运而生。常见形式有变摩擦阻尼器和分级屈服阻尼器等。变摩擦阻尼器可根据变形大小改变自身的摩擦力,以提供更大的耗能需求,用以解决摩擦阻尼器由于摩擦力设定过高,摩擦装置不能起滑,无法起到耗能减振的作用,或摩擦力设定过低,无法提供所需要的阻尼力的问题[27]。常通过摩擦面类型、角度的变化实现输出阻尼力的变化[28-29]。分级屈服阻尼器多用于改善金属阻尼器耗能水准单一及只能在中震或大震下屈服耗能的缺点,不同屈服位移的金属逐次进入塑性阶段耗能以达到分级屈服效果[30-31]。以上分级设防阻尼器都是以提高耗能水平的方式满足较高地震水准要求,并没有考虑结构震后自复位能力。

因此,为了有效的实现结构的分阶段抗震,满足可恢复功能结构四水准抗震设防目标,本文发展了一种新型具有变滞回性能的自复位耗能阻尼器。阻尼器在小变形下仅为结构提供刚度和强度,变形增加后阻尼器的滞回曲线呈现饱满的矩形,为结构提供稳定良好的耗能能力,随着变形进一步增大,阻尼器的滞回曲线呈现典型的旗帜型,同时具有优良的自复位功能,进而实现附加新型阻尼器结构的分级抗震的目的。

2 SMA-VHD的结构构造和工作机理

基于SMA板环的变滞回性能阻尼器(SMA-VHD)由摩擦模块和自复位模块组成,用以实现良好的耗能功能和自复位功能。阻尼器由内芯、上半圆形外套管、下半圆形外套管、SMA板环、高强螺栓及端板组成,如图1所示。

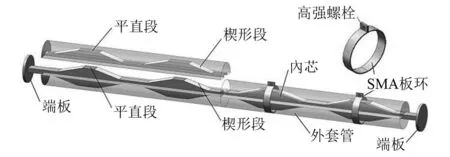
图1 SMA-VHD示意图Fig.1 Schematic diagram of SMA-VHD

摩擦模块包括内芯和上下半圆形外套管。两个半圆形外套管上下对合在一起形成整体的轴向水平的外套管,外套管凹槽内涂抹润滑油用以控制摩擦因数,两块相同的板状结构内芯置于其中。外套管内部有平直段和楔形段的凹槽分别与内芯平直段和楔形段相对应。自复位模块包括预紧SMA环和高强螺栓。外套管外侧沿径向采用SMA板环进行固定,在SMA板环的端部打有孔洞,通过预紧的高强螺栓对SMA板环施加预应变。

由于阻尼器结构构造上的对称性,SMA-VHD拉压工作机理相同,本文以受拉为例进行详细阐述。以阻尼器径向中心线为界,SMA-VHD左右两侧在结构上具备对称性,受力相同。因此,为简化分析,取单侧阻尼器隔离体进行受力分析,如图2(a)所示。L1为外套管平直段水平距离。L2为内芯楔形段水平距离,此距离与外套管楔形段水平距离相等。L3为内芯平直段水平距离。为避免内芯“滑脱”,应保证内芯与外套管之间表面贴合,因此阻尼器最大变形量(Δm,max)应满足

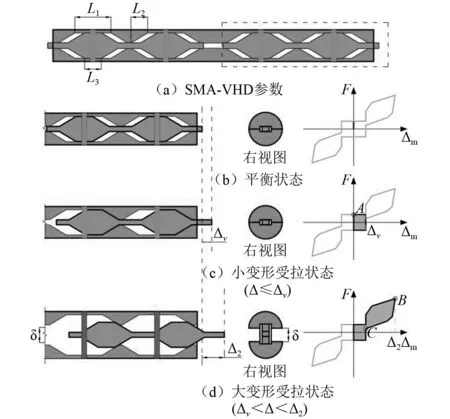
图2 SMA-VHD的工作机理及滞回曲线Fig.2 Working principle and hysteretic curves of SMA-VHD

Δm,max≤L2+L3/2

(1)

通过预紧螺栓对SMA板环施加预压力使SMA板环产生的变形量为Δs,0,则阻尼器隔离体总变形量(Δm)与SMA板环的受拉变形量(Δs)满足

Δs=4(Δm-Δv)tanθ+Δs,0

(2)

其中

Δv=(L1-L3)/2

(3)

式中:Δv为变滞回位移;θ为内芯楔形段角度。

SMA板环内力(Fs)与SMA板环对阻尼器隔离体外套管的压力(FN)之间满足式(4)关系

FN=2nFs

(4)

式中,n为阻尼器隔离体中SMA板环的个数。

将阻尼器隔离体受拉过程分为三个状态阶段:

(1) 平衡状态

当作用在阻尼器上的外荷载小于内芯平直段与外套管内部凹槽的平直段之间静摩擦力时,阻尼器处于平衡状态,如图2(b)所示。内芯与外套管之间没有相对位移。此时内芯、外套管以及预紧的SMA板环共同为阻尼器提供初始刚度。

(2) 小变形受拉状态

变形量小于Δv为小变形受拉阶段,如图2(c)所示。阻尼器外套管内部凹槽平直段与内芯平直段之间产生轴向位移,二者接触面发生滑移进而产生摩擦力。阻尼器在此阶段达到屈服点时(A点),屈服力Fy为

Fy=4nμFs,0

(5)

式中:μ为内芯与外管之间的摩擦因数;Fs,0为SMA板环中的预拉力。

(3) 大变形受拉状态

变形量大于Δv且小于Δ2为大变形受拉阶段,如图2(d)所示。此时,外套管内部凹槽楔形段与内芯楔形段之间发生相对滑移,阻尼器通过二者接触面滑移产生摩擦力耗能,同时上下外套管之间出现间隙(δ)。随着δ增大,SMA板环因受拉变形量增加,使得内芯与外套管之间的径向压力增大,摩擦力与耗能量随之增加。外力卸载后,SMA板环超弹性使得内芯复位到小变形受拉状态,实现自复位。

图2(d)中B点对应阻尼器隔离体变形最大时,此时阻尼器可提供的恢复力为峰值承载力Fmax。C点为内芯复位至小变形受拉状态的时刻,此时阻尼器的恢复力为卸载力Funload,对应位移为变滞回位移Δv。二者满足式(6)～式(7)

(6)

(7)

式中,Fs,max为SMA板环内力最大值。

3 SMA-VHD的变滞回性能

3.1 SMA板的材性试验

SMA具有形状记忆效应、超弹性和阻尼特性等优异的力学性能[32]。图3为SMA的简化本构模型[33],该曲线主要由四个特征点表征:相变应力σM,s、σM,f及其对应应变εM,s、εM,f分别为马氏体正相变转变阶段开始时(A点)和结束时(B点)的应力应变,相变应力σA,s、σA,f及其对应应变εA,s、εA,f分别代表马氏体逆相变转变阶段开始时(C点)和结束时(D点)的应力应变。

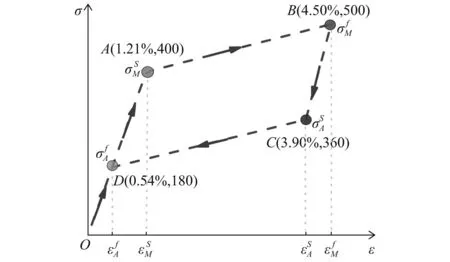
图3 SMA简化本构模型Fig.3 Simplified constitutive model of SMA

为确定SMA本构模型的特征点参数,对SMA板材进行力学性能试验研究。板材试件工作段截面为20 mm×10 mm的矩形,长度为150 mm。板材经超弹性训练、热处理、冷淬后进行循环拉伸加载测试,循环拉伸应变加载由1%逐级加载至5%,每级增量0.5%,如图4(a)所示。试验获得SMA板材试件的力与位移曲线如图4(b)所示。SMA板材的滞回曲线表现出典型“旗帜型”特征,卸载完成后几乎无残余位移。

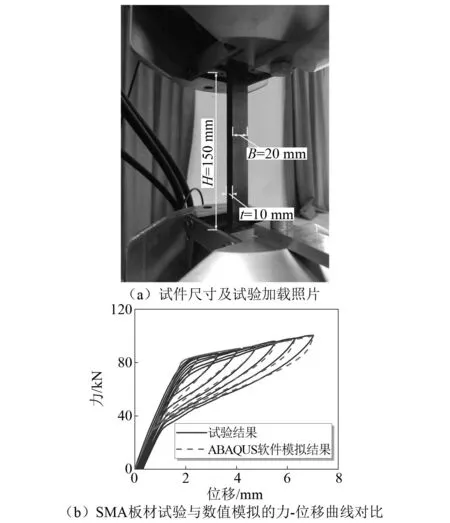
图4 SMA板材试验Fig.4 Test of the SMA plate specimens

在ABAQUS软件中建立与试验尺寸相同的SMA板材实体模型并赋予Super Elasticity本构模型,SMA本构模型特征点参数数值标定如图3所示,对其施加与试验相同的位移加载机制。将ABAQUS软件模拟结果与试验结果对比(如图4(b)所示),模拟结果与试验结果吻合良好,表明采用Super Elasticity本构模型能较好地适用于SMA板材的非线性本构关系。

3.2 有限元模型

3.2.1 阻尼器的设计

假定SMA-VHD的最大变形为100 mm。其中,阻尼器单侧隔离体的最大变形为50 mm,变滞回位移Δv为15 mm。尺寸设计满足以下要求:一是保证阻尼器楔形段实现完全自复位,即卸载力Funload大于零;二是避免SMA完成马氏体相变后卸载积累残余应变,在阻尼器达到最大变形量时,SMA板环的直径R应满足式(8)

(8)

阻尼器的尺寸。其中内芯楔形段角度θ=10°,板环的厚度h=10 mm,对SMA板环施加应变0.61%,如图5所示。

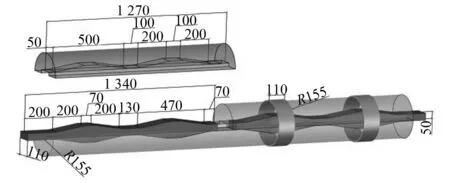
图5 SMA-VHD尺寸图(mm)Fig.5 Dimension of SMA-VHD (mm)

3.2.2 有限元模型的建立

SMA-VHD实体有限元模型如图6所示。所有实体部件采用C3D8R(线性缩减积分单元)模拟。SMA-VHD的内芯和上下外管均使用理想弹塑性本构模型,弹性模量(E)为2.1×105MPa,屈服强度(fy)为345 MPa,极限强度(fu)为540 MPa[34]。SMA板环采用ABAQUS软件内置的Super Elasticity本构模型,其本构关系的特征点参数依据3.1节确定。内芯与外套管对应平直段及楔形段接触面之间的接触关系采用“Surface-to-surface contact”模拟,切向行为选用“Penalty”以模拟摩擦行为,摩擦因数取0.1[35],法向行为模式为“Hardcontact”,通过“Interferencecontact”模拟高强螺栓拧紧施加给SMA板环的预应变。模型加载制度如图7所示。

图6 SMA-VHD有限元模型Fig.6 Finite elements model of the SMA-VHD

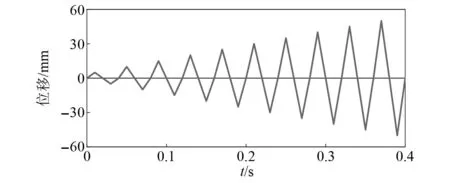
图7 加载制度Fig.7 Loading protocol

3.3 滞回性能

图8给出了SMA-VHD在拉压往复循环荷载下的滞回曲线。滞回曲线呈现出明显的“变滞回性能”。加载位移较小时,SMA-VHD处于弹性状态,此时荷载与位移呈线性关系。随着加载位移增大,SMA-VHD进入屈服阶段,开始耗能,此时滞回曲线饱满近似矩形。随着加载位移进一步增大,滞回曲线呈旗帜型,自复位效果良好,卸载时无明显的刚度和强度退化。滞回曲线整体显示出“变滞回性能”,滞回曲线矩形部分及旗帜型部分之间具备清晰的分级平台。同时,图8也给出了SMA-VHD滞回曲线理论计算与数值模拟结果对比图,二者吻合结果良好。

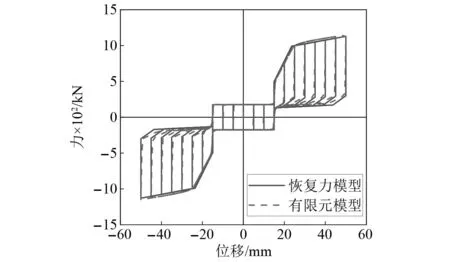
图8 SMA-VHD恢复力模型与有限元模型滞回曲线对比Fig.8 Hysteretic curve comparison between restoring force model and finite element modelof SMA-VHD

摩擦因数对SMA-VHD滞回曲线的影响规律如图9(a)所示,增大内芯与外管之间摩擦因数,可提高SMA-VHD的屈服力Fy及峰值承载力Fmax,滞回曲线更加饱满。但是,当摩擦因数过大时Funload成为负值,此时阻尼器将失去自复位能力。图9(b)给出了楔形段角度对SMA-VHD滞回曲线的影响规律,随楔形段角度增加,Fmax及Funload提高。

图9 SMA-VHD关键参数对其滞回性能的影响Fig.9 The influence of key parameters of SMA-VHD on hysteresis performance

增大施加在SMA板环上的预应变εf,0可提高Fy和Funload,如图9(c)所示。但是,当εf,0=1.21%时,即马氏体正相变转变阶段开始时的应变εf,A,Fy在循环加载中会逐渐变小。因此建议施加在SMA的预应变区间为εf,0≤εf,A。平直段长度(l)对SMA-VHD的影响规律如图9(d)所示。平直段长度的增加会增大变滞回位移Δv,同时提升了阻尼器的变形能力。但Δv后滞将增大SMA-VHD的残余位移。

4 阻尼器在RC桥墩结构中的应用

4.1 RC桥墩结构

本文选取的桥墩模型参数参考文献[36]的山区实际排架墩。桥墩墩柱高度为6 400 mm,横截面为1 000 mm×1 000 mm的矩形,双柱之间的净距为13 000 mm,混凝土等级选用C40,保护层厚度50 mm;墩柱纵筋选用HRB400,直径为32 mm,墩柱截面的纵筋配筋率为0.96%,箍筋选用HPB300,直径为8 mm,间距为100 mm。

本研究使用ABAQUS软件建立排架墩的有限元模型。为验证建模方法的正确性,选取参考文献[36]中桥墩缩尺模型拟静力试验结果作为对比对象。有限元模型各部件均采用三维实体单元,混凝土单元类型为C3D8R(三维实体线性减缩积分),钢筋单元类型为T3D2(两节点线性三维桁架单元)。盖梁与墩柱、墩柱与承台间均使用“Constraint”约束。模型中C40混凝土采用塑性损伤本构模型,弹性模量为3.25×104 MPa,钢筋弹性模量均为1.9×105 MPa,本构采用理想弹塑性模型。HRB400钢筋的屈服强度为360 MPa,HPB300钢筋的屈服强度设置为270 MPa。数值模拟结果与试验结果吻合良好,证明了建模方法的正确性,如图10所示。

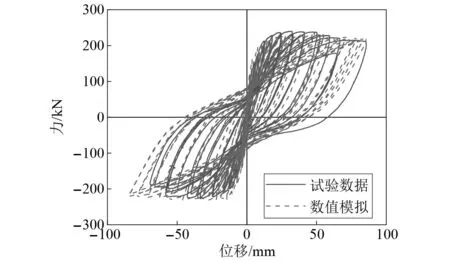
图10 数值模拟与参考文献[34]试验数据结果对比图Fig.10 Comparison between experimental data from reference [34] and numerical simulation results

基于上述方法建立原型排架墩的有限元模型,并对该模型进行Pushover分析。获得桥墩屈服力Fyp=2 790 kN, 屈服位移Δyp=35 mm,极限位移Δd=300 mm,极限位移下的残余位移为209 mm。

4.2 阻尼器的设计

将SMA-VHD以“人字形”形式布置在排架墩中。在ABAQUS软件中使用“Connector”模拟阻尼器,如图11所示,在相同位移加载机制下,SMA-VHD实体有限元模型与“Connector”模型的滞回曲线吻合程度良好,进而将“Connector”附加于排架墩结构中用于模拟SMA-VHD,如图12(a)所示。

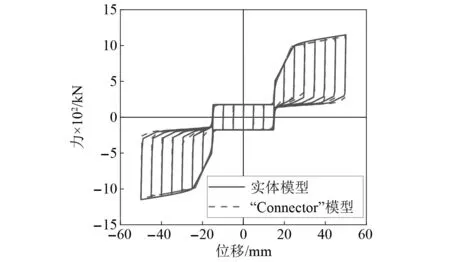
图11 SMA-VHD实体有限元模型与“Connector”模型滞回曲线对比Fig.11 Comparison of hysteretic curves of SMA-VHD between solid finite element model and “Connector” model

图12 附加SMA-VHD的排架墩Fig.12 Double-column bent with additional SMA-VHDs

图12(b)给出了SMA-VHD与排架墩结构变形的关系。阻尼器变形量(Δm)与桥墩变形量(Δ)之间的关系满足式(9)

(9)

附加SMA-VHD的排架墩要有稳定的耗能能力和可恢复性,因此SMA-VHD设计应该满足以下三点原则:

(1) SMA-VHD作为桥墩的牺牲元素,SMA-VHD须在桥墩屈服之前屈服,因此SMA-VHD的屈服位移Δv,y(图2中A点位移)满足式(10)

Δv,y≤ΔY

(10)

式中, ΔY为原桥墩屈服位移。

(2) SMA-VHD应使桥墩的残余侧移率控制在0.5%的范围内[37],因此SMA-VHD的变滞回位移Δv需要满足式(11)～式(12)

(11)

(12)

(3) SMA-VHD的恢复力满足桥墩复位需求,即SMA-VHD卸载力Funload的水平分力满足式(13)

2Funloadcosα≥Fyp

(13)

式中:Fyp为原桥墩的屈服荷载;α为SMA-VHD与水平的夹角。

作为对比参照,同样使用“Connector”模拟BRB[38]、自复位耗能支撑(self-centering energy brace, SCB) 附加于桥墩之间。三种阻尼器具备相同的屈服荷载及初始刚度,屈服荷载为2 000 kN,初始刚度为100 kN/mm。BRB与SCB的屈服后刚度为初始刚度的1%。在SMA-VHD达到变滞回位移前,SMA-VHD与BRB的耗能量相近且远大于SCB;SMA-VHD达到变滞回位移后,恢复力模型呈现典型的旗帜型。三者恢复力模型如图13所示。

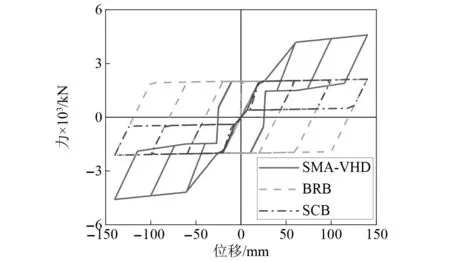
图13 BRB、SCB及SMA-VHD的恢复力模型Fig.13 Restoring force model of BRB, SCB and SMA-VHD

4.3 附加SMA-VHD桥墩结构的分级抗震性能

结构在近场地震动作用下的破坏较远场地震动更为显著[39-41],本文选取两个不同台站的近场对称性脉冲地震动Rinaldi和近场非对称型脉冲地震动CHICHI_Taiwan记录。参考我国第五代《中国地震动参数区划图》[42],将地震作用定义为四级地震烈度水准,即多遇地震动、基本地震动、罕遇地震动及极罕遇地震动,因此本文将选取的原始地震动记录按照地震动峰值加速度PGA调整为0.1g(多遇地震)、0.3g(基本地震)、0.58g(罕遇地震)、0.9g(极罕遇地震)四个等级。地震动记录在PGA为0.3g时的加速度、速度、能量通量时程曲线如图14所示。

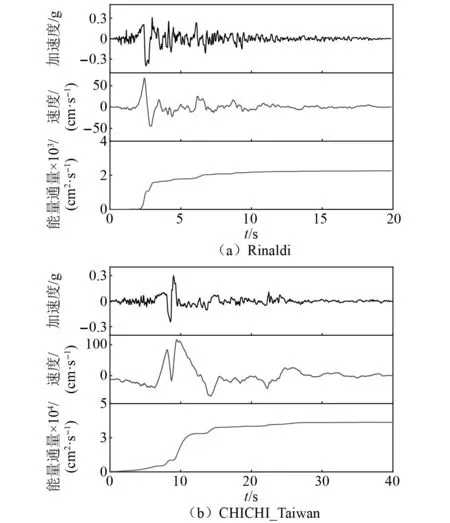
图14 输入地震动时程曲线(PGA=0.3g)Fig.14 Inputting time history curves of ground motions (PGA of 0.3g)

桥墩的最大变形将直接决定其地震损伤破坏程度[43],残余变形可直接反映墩柱产生非线性变形后的复位能力[44]。因此,取桥墩峰值侧移率及残余侧移率作为附加阻尼器桥墩抗震性能提升评价指标,并根据桥墩震后损伤状况将其分为五个等级:完全破坏、严重损伤、中等损伤、轻微损伤和无损伤,以最大侧移率作为损伤指标时对应的各损伤极限状态值如表1所示[45]。残余侧移率选用0.5%作为损伤极限状态值。

表1 最大侧移率对应的损伤极限状态Tab.1 Damage limit state of maximum drift ratio

图15给出了近场对称型脉冲地震动作用下桥墩位移时程曲线及滞回曲线,图16展示了不同PGA地震动下桥墩最大侧移率和残余侧移率的柱状图。由图15及图16(a)可知,桥墩的峰值侧移率随PGA等级增大而增加。附加阻尼器可有效降低桥墩的最大侧移率。由图15(a)可知,在PGA为0.1g地震动作用下,与原桥墩相比,RC-BRB、RC-SCB和RC-SMA-VHD桥墩峰值侧移率明显下降,且近似相等。根据图15(b)中的滞回曲线显示,RC-BRB、RC-SCB和RC-SMA-VHD均处于弹性阶段。当PGA增大到0.3g时,如图15(c)所示,RC-BRB与RC-SMA-VHD的峰值侧移率相近且均小于RC-SCB,RC-SMA-VHD与RC-BRB耗能水平近似(如图15(d)所示)。当PGA为0.58g及0.9g时,如图15(e)及图15(g)所示,RC-BRB与RC-SMA-VHD的峰值侧移率相近且均小于RC-SCB。由图16可知,RC桥墩达到倒塌极限状态,RC-SCB达到严重损伤状态,RC-BRB在0.9g时达到了中等损伤,而RC-SMA-VHD桥墩仍处于轻微损伤状态。

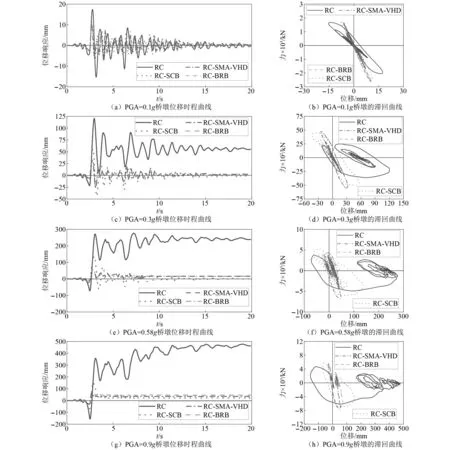
图15 近场对称型脉冲地震动作用下桥墩位移时程曲线及滞回曲线Fig.15 Time-history responses and hysteretic curves of bridge bent under near-field symmetric pulsed earthquake

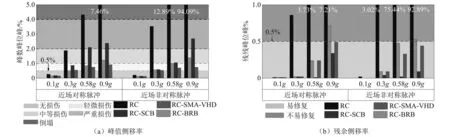
图16 不同PGA地震动下桥墩最大侧移率和残余侧移率Fig.16 Maximum drift ratio and residual drift ratio of bridge bent under ground motions with different PGAs

由图15及图16(b)可知,类似的,附加阻尼器桥墩的残余变形均明显小于原桥墩,且桥墩的残余侧移率随着PGA等级增大而增加。当PGA为0.1g时,四种桥墩的残余侧移率均较小;当PGA增大到0.3g和0.58g时,RC桥墩残余侧移率超过0.5%限值,RC-BRB与RC-SMA-VHD残余侧移率相近,RC-SCB的残余侧移率最低;当PGA达到0.9g时,RC-BRB的残余侧移率超过0.5%,而RC-SMA-VHD的残余侧移率始终控制在0.5%的范围内。

由图16可知,结构在近场对称型脉冲地震动作用及非对称型脉冲地震动作用下的最大侧移率及残余侧移率没有一致性规律。如当峰值加速度为0.3g和0.58g时,RC-SCB在近场对称型脉冲地震动下的最大侧移率大于近场非对称型脉冲地震动,但当峰值加速度为0.9g时,RC-SCB在近场对称型脉冲地震动作用下最大侧移率小于近场非对称型脉冲地震动。当峰值加速度为0.58g时,RC-SMA-VHD在近场对称型脉冲地震动下的残余侧移率小于近场非对称型脉冲地震动,但当峰值加速度为0.9g时,近场对称型脉冲地震动残余侧移率更大。

综上所述,SMA-VHD在多遇地震下保持弹性状态,为结构提供附加刚度和强度;基本地震作用下为结构提供稳定良好的耗能能力,从而减小结构的地震响应;随着地震作用加剧,阻尼器可在罕遇地震和极罕遇地震下为结构提供稳定耗能能力的同时,还能提供优良的自复位功能,进而减小结构的残余变形。因此,附加SMA-VHD可有效实现结构分级抗震的目的,进而提高结构的抗震能力。

5 结 论

为了实现分级抗震,本文基于SMA板材提出了一种变滞回性能阻尼器(SMA-VHD)。基于新型阻尼器的结构构造和工作机理,理论公式推算得到了该阻尼器的恢复力模型,进一步对阻尼器滞回性能及参数影响规律进行研究,最后将阻尼器应用于RC排架墩中,研究其对桥墩分级抗震性能提升效果。具体结论如下:

(1) 新型变滞回性能阻尼器(SMA-VHD)的滞回曲线呈现明显的分级平台,在小变形时,滞回曲线呈现饱满的矩形,耗能能力强;随着变形进一步增大,阻尼器的滞回曲线呈现典型的旗帜型,同时具有优良的自复位功能。

(2) 增大内芯与外管之间摩擦因数可提高阻尼器的强度和耗能能力,但超过上限会导致阻尼器无法自复位;楔形段角度增加可使阻尼器的强度提升;对SMA板环施加的预应变应满足εf,0≤εf,A;通过调整平直段长度可以改变变滞回位移以满足结构的不同需求。

(3) 在多遇地震和基本地震作用下,SMA-VHD可为桥墩提供良好的耗能能力,附加SMA-VHD可有效降低桥墩的最大侧移率,附加SMA-VHD桥墩的峰值侧移率与附加BRB的桥墩相近;罕遇地震和极罕遇地震时,SMA-VHD还可为桥墩提供良好的自复位功能,附加SMA-VHD桥墩的残余侧移率明显低于附加BRB的桥墩,并将残余侧移率始终控制在0.5%的范围内,附加SMA-VHD可有效实现结构的分级抗震目的。

限于篇幅,本文对变滞回性能阻尼器的恢复力模型、滞回性能及参数影响规律进行了系统性研究,并将其应用于RC排架墩中,研究其对桥墩分级抗震性能提升效果。为了进一步验证阻尼器的性能,将在后续研究中开展新型阻尼器的拟静力试验,并对附加新型阻尼器的结构的失效概率进行详细系统地研究分析。