面向传动性能的分体式RV减速器结构优化*
杨晨昊,王金栋,李 澳,唐雷雨
(西南交通大学机械工程学院,成都 610031)
0 引言
RV减速器作为精密传动装置的一种,由行星轮传动和摆线针轮传动组成,具有大传动比、高负载、高传动精度等优势,被广泛运用在工业机器人的生产加工中[1]。国产RV减速器起步较晚,在技术层面与国外厂商还有一定差距[2]。作为精密传动的一种,复杂的修形方法、严苛的公差要求是制约国产RV减速器发展的原因[3]。
在提高RV减速器传动性能的问题上,国内外学者开展了诸多研究。为提高RV减速器的传动精度与可靠性,于明以减速器整体体积最小化为设计目标,将关键零部件的主要尺寸作为设计变量的同时保持传动比与输出功率不变完成RV减速器的结构设计[4]。张诚针对RV减速器传动精度问题,为减小回差对传动过程的影响,将减速器的几何回差作为研究目标,各零部件的主要公差项作为设计变量建立优化设计模型[5]。WANG等[6]以体积和效率作为优化目标,使用遗传算法对单级摆线减速器,进行多目标优化设计。由于常见RV减速器减速比固定不能适应复杂工况,黄津晶提出了一种传动精度高、结构紧凑且力学性能良好,能够实现传动比可变的变传动比RV减速器[7]。针对RV减速器工作过程中振动噪声的问题,CHEN等[8]通过建立集中参数的动力学模型分析陀螺效应与关键几何尺寸对RV减速器自由振动特性的影响。王新春[9]在对摆线轮齿廓传统修形方法深入研究的基础上,提出了一种基于摆线轮齿廓二次包络理论的等移距组合修形量计算的新方法,大大提高了摆线轮齿廓修形量的计算精度。HUANG等[10]通过建立非线性约束优化模型对RV减速器轴承进行优化设计,以提高RV减速器工作寿命,避免发生疲劳失效。传动效率是限制现代RV减速器发展的重要原因,WANG等[11]通过推导一种RV减速器传动效率的计算方法,建立体积-效率目标函数,实现RV减速器高功率密度设计。LIU等[12]分析了同轴度误差对RV减速器的影响,设计了一台高精度检测装置,建立RV减速器同轴度-几何回差模型,揭示了同轴度对几何回差的影响规律。宿月文等[13]对RV减速器传动误差进行建模,对减速器传动误差影响小的尺寸参数的误差等级进行修正,在保证传动精度的同时有效降低了减速器的加工误差。丁国龙等[14]建立了RV减速器传动误差与固有频率的数学模型,揭示了RV减速器模态对传动误差的影响规律。
通过上述分析可以看出目前研究人员关注的重点主要集中在传动构件结构优化、摆线轮齿廓修形,通过以上方式提高机构的可靠性和传动精度。伴随着传动精度的提高,摆线轮齿廓曲线也愈加复杂,减速器尺寸参数的精度要求也逐渐严苛,致使关键零部件的加工工艺复杂、加工难度大。因此在保证传动精度的同时,如何降低RV减速器加工难度,提高传动效率是亟需研究的关键问题。
本文在分析RV减速器工作原理的基础上,提出一种分体式RV减速器设计方法,并进一步推导结构尺寸与系统受力间的关系,通过遗传算法对减速器各项尺寸进行优化实现面向性能的RV减速器结构设计。并利用虚拟样机仿真对设计方案的合理性进行验证。
1 RV摆线轮结构与减速器总体设计
1.1 摆线轮结构分析
如图1a所示,标准摆线轮的齿廓是一条连续的摆线,加工方法为数控铣削、冷挤压、成形磨削工艺等。

(a) 标准摆线轮 (b) 分体式摆线轮
如图1b所示,连续齿廓离散后,摆线轮轮齿被圆柱滚针替代,与摆线轮齿相比滚针的外形轮廓更简单,加工方法为车削与钻孔。
1.2 减速器总体设计
1.2.1 减速器传动比分配及齿轮基本参数的计算
RV减速器是一种大传动比、高效率传动机构,针齿壳固定,太阳轮输入,行星架输出时,传动比为:
(1)
式中:i为传动比,z1为太阳轮齿数,z2为行星轮齿数,z4为外壳针齿齿数。
在RV减速器工作过程中,摩擦损失是影响传动效率的主要原因,功率从输入轴经齿轮啮合、轴承转动与针齿啮合到达输出轴。功率损失可以划分为齿轮啮合摩擦损失和滚动轴承摩擦损失,因此RV传动的传动效率为:
η=η16ηB
(2)
式中:ηB为轴承总效率且ηB=ηB1ηB2ηB3,ηB2为转臂轴承效率,取0.99;ηB2为曲柄支撑轴承效率,取0.99;ηB3为行星架支撑轴承效率,取0.99;η16为RV啮合效率与减速器传动比相关,因此:
(3)

通过对传动效率公式分析可知,渐开线齿轮传动的传动比对传动效率有较大影响,在选择传动方案时需要对传动比进行控制。
通过对RV减速器运动封闭的特点以及两级传动机构分析,可以得到减速器的基本几何约束条件:
(1)摆线针轮机构作为差齿传动的一种,大传动比会影响减速器的整体体积与重量,导致摆线轮齿廓负载,提高零部件的加工难度。进而影响RV传动的传动精度与承载能力,为保证其传动比不会过大,行星减速机构的传动比满足:u=z2/z1>1.5。
(2)在行星齿轮传动过程中,为保证各曲轴传动过程中的同步性,太阳轮齿数是行星轮数量的整数倍。在渐开线行星传动机构中,为保证齿轮不发生根切且保证轮齿的磨损,根据变位系数、齿顶厚以及齿数之间的关系,中心轮齿数z1的选取范围为[9,20][15]。
(3)为保证传动过程中,行星轮的齿顶圆间不发生干涉,行星轮齿顶圆应满足:da<2asinπ/n。
(4)在传动过程中轮齿应不发生胶合或折断,太阳轮模数m应满足弯曲疲劳强度校核,分度圆应满足接触疲劳强度校核。
综合上述约束条件,确定减速器的主要结构参数,计算流程图如图2所示。

图2 主要参数计算流程图
通过图3所示的计算方法进行参数迭代计算,能够得到多组符合条件要求的几何参数,如表1所示。

表1 符合约束条件的几何参数方案

表2 选择的几何参数方案

图3 摆线轮受力分析
在选择传动比分配方案时,为保证运动平稳性、传动效率与前后端工作寿命相同,机构整体尺寸小,一二级减速机构的结构尺寸应尽量相同,传动效率应保持较高水平。因此应选择第3个传动方案。
1.2.2 关键尺寸设计
(1)关键零部件受力分析。
①摆线轮受力分析。在曲轴自转下,摆线轮通过偏心运动与针齿啮合在运动过程中,认为在摆线轮、曲柄、滚动轴承等零部件不存在尺寸误差且材料处处均匀的理想状态下,可认为曲柄沿针齿对摆线轮的力FP方向上曲柄轴产生的弹性形变相等。即曲柄轴承处FP方向上的受力均为FP/3;同时为抵消FP对摆线轮产生的扭矩,各曲柄轴承处沿摆线轮周向的受力也相等。如图4所示,结合上述分析,曲柄受力的大小相等,合力与曲柄转角θ有关。由此可得:
(4)

(a) 径向受力分析 (b) 轴向受力分析

图5 减速器主要几何约束

(a) 曲轴 (b) 摆线轮 (c) 针齿壳 (d) 装配体
式中:a为齿轮中心距,rRV为摆线轮半径,αc为FP与摆线轮圆周切向的夹角。
②曲轴受力分析。由图4b所示,通过摆线轮受力分析与力矩平衡方程可知作用力Fi1、Fi2和Fn已知,只有曲轴两端的FG1、FG2未知,通过水平面与垂直面的力与力矩的平衡方程可得式(5)。
(5)
式中:bB为曲轴两端轴承厚度,bD为曲柄处轴承厚度,bP为行星轮齿厚,Fnx与Fny为齿轮见啮合力在x、y方向上的分量。
(6)
通过以上受力分析,结合减速器工作原理,3根曲轴对输出轴的扭矩应满足设计要求即:
(7)
对上述方程组求解可得:
M=2FPrRVcosαc
(8)
如图4a所示,取任一曲轴及与其相固联的行星轮为分离体,由力矩平衡方程可知:
(9)
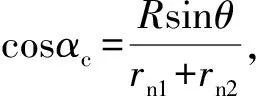
(10)
传动过程中齿轮啮合力Ft、针齿啮合力FP、曲柄轴受力Fi、支撑轴承轴力影响FG,各力的表达式如式(11)所示。
(11)
(2)减速器关键参数分析。为保证RV减速器的体积、工作寿命符合设计要求,提高减速器的可靠性,针齿分布圆尺寸R应取值65,针径系数K1应取值0.6。因此针齿壳上针齿直径rn1应为rn1=KR=2.57。
分体式摆线轮的主要参数为:R、e、rRV、rn1、rn2。摆线轮传动是依靠各对针齿的依次啮合来实现的,为保证摆线轮能够连续传动,工作过程中应始终有至少一对针齿啮合,即实际啮合线的长度与针齿齿距的比值大于1。
为保证RV减速器在传动过程中不发生干涉,任一针齿与相邻针齿间距离应大于针齿直径且针齿壳与摆线轮间应保留间隙,即:
①传动过程中针齿壳上针齿与摆线轮间距离应大于0。
R>rRV+e+rn1
(12)
②传动过程中摆线针轮机构能够发生啮合。
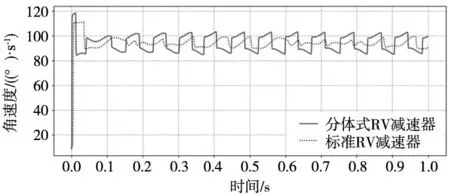
R (13) ③传动过程中针齿间不能发生干涉。 R>rRV-e+rn1+rn2 (14) (15) ④回差是减速机精度标志之一,RV减速器的回差由几何回差、温度回差与弹性回差组成。其中几何回差与传动构件间的装配空隙直接相关。为保证减速器的回差,针齿啮合时摆线轮各尺寸应满足: (16) 综合上述分析,在K=1.67、R=59时,可得: 偏心距e在(1.42,1.48)的取值范围内满足几何约束,由上述分析可知伴随偏心距增大,减速器各处受力最小,同时在e=1.48时摆线针轮机构的回差最小。因此减速器各尺寸应为: (17) (3)轴承选型与关键零件设计。通过RV减速器受力分析可求解各部件受力为: (18) 由此曲柄轴承选用7004AC角接触球轴承,曲柄两端轴承选用30202圆锥滚子轴承,输入轴与输出轴轴承选用角接触轴承71820AC。从而完成曲轴与连接盘的结构设计。 针对RV减速器衡量其性能的几个关键技术参数有:负载性能,传动效率,传动精度等。为使减速器的性能达到理想效果,需要调整减速器的尺寸参数以进行结构尺寸优化。在求解过程中可以通过启发式算法来求解。 NSGA是一种随机全局搜索优化方法,从初始种群出发,通过模拟自然选择和复制、交叉和变异等现象,产生一群更适合环境的个体,使群体进化到搜索空间中越来越好的区域,经过迭代,最后收敛到一群最适应环境的个体,从而求得问题的优质解。 2.1.1 目标函数 (1)正向传动精度。分析RV减速器的运动可知,太阳轮带动3个与偏置方向相同的曲柄轴固连的行星轮,同时在曲柄轴驱动摆线轮转动时,曲柄轴与摆线轮铰接点间的距离始终为定值,且等于相邻行星轮间的距离,因此这个曲柄轴的转动可视为以曲柄轴偏距为共用邻边的3个平行四边形机构,通过对RV减速器结构进行高副低代得到等效杆长模型,如图7所示。 图7 等效杆长模型 将平行平面中的运动机构组合到同一平面中得到简化模型,如图8所示。 在不考虑加工误差与装配误差时,运动学模型可表达为: (19) (2)传动效率。在RV减速器工作过程中,传动效率模型如式(2)所示。 (3)反向传动精度。RV减速器是由行星传动与摆线轮差齿传动组成的闭环差动轮系,因此误差计算包括行星轮系的回差与摆线针轮轮系的回差。 其中齿轮传动部分的回差主要由齿侧间隙造成,且回差经过摆线轮系会缩小为摆线轮系传动比的倒数,由国家标准可知齿侧间隙的取值为: (20) 因此齿轮传动造成的回差为: (21) 摆线传动部分的回差为: (22) (23) (4)负载性能。由于摆线轮轮齿的离散化,齿侧间隙被放大,使同时啮合的齿数减少。初始啮合间隙的计算公式为: (24) 在对摆线轮加载扭矩后,摆线轮与针齿产生接触变形,摆线轮转过一个角度β: (25) 如图9所示,初始间隙小于该角度的齿都参与啮合,齿侧间隙曲线为图中实线,转动角度曲线为图中虚线,在交点内的齿是进入啮合且受力的齿。 图9 啮合齿数 由赫兹公式可知,弹性变形量与受力的关系为: (26) 因此RV减速器的负载性能为: (27) 2.1.2 设计变量 由减速器运动学模型,以曲柄轴偏心距e、摆线轮基圆半径rv、针齿分布圆半径r、摆线轮针径系数k1、针齿壳针径系数k2和摆线轮齿厚b,设计变量基因型可表示为: x=[e,rv,r,k1,k2,b] (28) 2.1.3 约束条件 受加工条件与实际结构约束,设计变量存在取值范围,不同设计变量间存在相互约束关系。 (1)为保证针齿壳与针齿之间的机械强度,同时避免针齿相撞,需要对针齿分布的稠密程度进行描述。在此引入针径系数K1,通过针齿分布圆上相邻两针齿中心间的距离与针齿直径的比值来表示: (29) 式中:K1⊂(1.5,2)。 (2)齿轮模数符合国标推荐模数; (3)传动过程中零部件不发生干涉: (30) r>rv+e+r1 (31) (4)满足连续传动条件: r-e-rv≤r1+r2 (32) 对于针径系数与齿轮模数等约束条件,通过设置取值上下限,连续传动条件与干涉问题通过构造罚函数对样本适应度进行修正。 f1=-e(r-e-rv-r1)2-r2(r-e-rv-r1) (33) (34) 由于尺寸参数优化具有多目标优化的特点,因此评价方法的不同会影响最终的计算结果,常见的评价方法是对不同优化目标分配权重,根据权重计算出评价最高的结果。但机构优化设计时,由于目标函数间存在相互冲突,会导致减速器尺寸结构失调,迭代结果无法使用。 因此,引入Pareto支配的概念,通过设置设计参数与目标函数的接受区间,若迭代结果无法在改进任何目标函数的同时不削弱至少一个其他目标函数时称作Pareto最优解并接受。 在迭代过程中,为保证求解结果时全局最优,对迭代结果进行非支配排序,在同一层次的样本进行拥挤度计算,对密集分布的样本进行抽取,以保证样本基因型的多样性。拥挤度计算方法为: c=∑Δfi (35) 算法计算流程如图10所示。 图10 优化过程 通过NSGA-Ⅱ算法求解RV减速器结构参数的Pareto解。整体优化过程和各子目标的优化过程如图11~图15所示。 图11 优化流程 图13 反向传动精度优化过程 图15 传动效率优化过程 图16 RV减速器装配体模型 在计算结果中选取4组最优结果,如表3所示。 表3 NSGA计算结果表 (mm) 由于各目标函数之间存在冲突,且不同目标间优先级也存在不同,设计综合目标函数对优化问题进行描述,如式(36)所示。 Objective=∑(ωiXi)/SFi (36) 式中:权重系数ωi表征不同目标函数之间的优先级,比例因子SFi对各目标函数进行归一化处理避免不同目标之间存在较大数量级的差距。本研究以优化传动精度与负载性能为主,引入权重系数与比例因子如式(37)所示。 (37) 在计算结果中选择综合目标函数最小的一组解作为最优解。最终关键尺寸参数结果如表4所示。 表4 关键尺寸参数 (mm) 如表5所示,通过对比RV减速器优化前后性能变化可知,负载性能提升96.87%、反向传动精度提升26.8%,正向传动精度提升1.2%,传动效率提升2.19%。 表5 优化结果对比 利用虚拟样机仿真验证设计RV减速器的运动可行性与传动高效性,通过solid works分别对优化前后两种RV减速器进行参数化建模,在确保正确装配与无干涉后,将模型导入Adams并添加相关约束,通过不同转速、负载之间的相互组合设置多种工况,以探究转速、负载交互作用下RV减速器的传动性能的变化规律。 将RV减速器装配体模型以X_T格式导入ADAMS中,并给各关键零部件定义材料属性,RV减速器的材料属性如表6所示。 表6 RV减速器关键构件材料属性表 在对RV减速器施加几何约束后,设置RV减速器的太阳轮为转动驱动,仿真转速为2400 rpm,输出盘理论输出转速为95 (°)/s。同时设置输出端负载为空载,获得RV减速器输出端转速如图17所示,图中RV减速器输出端的实际转速与理论输出转速近似相等,可以说明模型内部运动传递关系正确,同时对比输出曲线可以看出,优化后RV减速器仿真结果相较于优化前RV减速器,由于针齿结构的几何特点,内部零部件的间隙能够得到有效控制,导致输出端的响应速度要快于优化前RV减速器。 图17 输出端实际角速度对比图 通过虚拟样机仿真,获得RV减速器在太阳轮输入转速2400 rpm下,输出轴负载425 N·m的工况下输出端角速度曲线,如图18所示。从图18a中可以看出,在相同工况下,减速器效率相同,由图18b和图18c可知,优化后减速器的曲柄轴与针齿等关键零部件受力更小,机构可靠性更高。 (a) 负载条件下输入轴扭矩 (1)针对摆线轮廓形复杂、加工难度大的问题,采用分体式摆线轮对减速器进行优化设计,建立RV减速器三维模型,以负载性能,传动精度,传动效率为评价指标,构建多目标评价函数,采用NSGA算法实现RV减速器最佳结构参数集成。 (2)对优化设计出的RV减速器进行动力学仿真与有限元仿真分析,动力学仿真结果表明设计出的RV减速器负载性能提升96.87%、反向传动精度提升26.8%、正向传动精度提升1.2%、传动效率提升2.19%,验证了设计方法的有效性。同时采用有限元对设计RV减速器结构的合理性进行了验证。2 尺寸参数优化
2.1 优化模型建立


2.2 Pareto支配
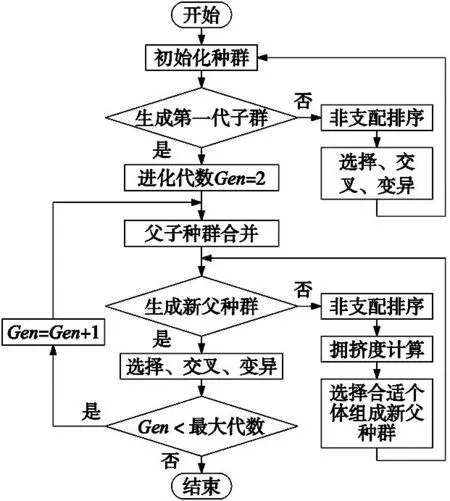
2.3 结果分析

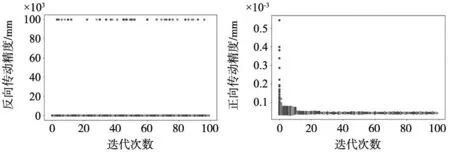
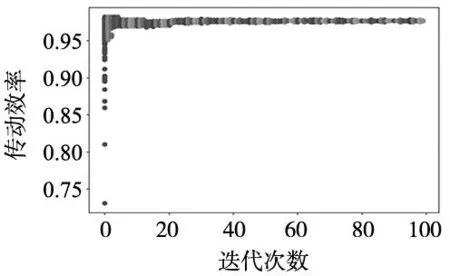




3 RV减速器仿真分析


4 结论

