基于改进MVO算法的电力无线专网基站选址

徐玉佳，张华美，2

（1.南京邮电大学电子与光学工程学院、柔性电子（未来技术）学院，江苏 南京 210023；2.东南大学毫米波国家重点实验室，江苏 南京 210096）

0 引 言

近年来，电力无线专网规模和复杂性不断提升，急需提高其通信传输能力来确保电力业务的正常开展。而提高电网通信能力势必会增加对基站的需求，基站规划不当会导致整个电力无线专网业务开展效率低、通信质量差等问题，因此合理的基站规划是网络规划中的重要任务之一［1］。

传统的基站选址方法主要依赖于工程师的经验，适用范围较小且准确率较低［2］，不能适应目前电力业务的通信需求。近年来，采用智能优化算法对基站选址问题进行优化已成为研究的重点和热点。

朱思峰等［3］在满足规划区域内部覆盖需求前提下以基站建设代价最小为目标，提出了一种基于免疫算法的基站选址优化方法；针对3G 基站选址方法的不足，张英杰等［4］继续改进免疫算法，利用改进的免疫算法求解基站选址方案；Li 等［5］根据TD-LTE 通信网络的特点，设计了一种基于免疫算法的基站选址优化方案；宋黎［6］运用遗传算法以解决无线网络中的基站规划问题，该方案在降低成本和覆盖盲区的同时提高了信号质量；Wang［7］将基站选址问题与粒子群算法相结合以解决能耗问题；唐丽晴等［8］以基站覆盖率为主要优化目标，将改进的鲸鱼优化算法应用到基站选址问题中。

单一的启发式算法后期搜索效率较低，其规划结果往往不能得到最佳的基站分布。随着研究的深入，目前着重于多个算法融合。刘娟等［9］将粒子群算法和果蝇算法结合，提高了基站覆盖性能。Zhou等［10］和冯佳勇［11］分别使用混合遗传贪心算法和模拟退火—遗传算法，在保证覆盖质量的前提下降低了成本预算。（这些混合）算法较单一算法极大地提高了优化质量。

本文参考的文献中有一部分考虑了覆盖和成本［10-17］。但是，因为TD-LTE 网络使用了同频组网方式［18］，相邻小区之间的重叠覆盖范围变大，同频干扰现象严重，导致业务终端频繁掉线，业务开展效率难以保证，因此本文除了考虑覆盖和成本，把重叠覆盖也加入到优化目标中，旨在降低同频干扰。

针对以上分析，本文提出一种基于改进的多元宇宙优化（Multi-Verses Optimizer，MVO）算法的基站选址方法。MVO 算法具有参数少、寻优效率高等优点，可用于解决多维度优化问题［19］。首先，基站选址是一类具有二进制解空间的优化问题，而基本MVO算法仅适用于连续域，因此本文采用V型转换函数进行离散化处理。其次，改进了算法中的TDR参数，平衡了算法的探索和开发能力。最后，将禁忌搜索算法融入到MVO 算法的寻优过程中，增强了算法摆脱局部最优的能力。仿真结果表明，本文算法对于解决基站选址优化问题具有较高的求解效率和卓越的性能优势。

1 基站选址建模

1.1 链路预算模型

采用COST 231-HATA 模型，1.8 GHz 电力无线专网传播模型的路径损耗公式为：

式中，PL 是路径损耗（dB）；f是频率（MHz）；hb是基站天线高度（m）；hm是终端天线高度（m）；d是终端与基站之间的距离（km）；a（hm）是终端天线高度校正因子；CM是环境校正因子。

参考信号接收功率RSRP（Reference Signal Receiving Power）是LTE 小区网络中接收功率电平的测量值，其公式为：

式中，PBS为基站发射功率（dBm）；G为基站天线和终端天线的增益之和（dB）；Lf+p+b为馈线损耗、穿透损耗、人体损耗之和（dB）；Mf+I为阴影余量和干扰余量之和（dB）。

本文以测试点的RSRP 作为衡量覆盖率的标准，若某个测试点的RSRP＜-105 dBm，则认为该测试点没有被基站覆盖。通过式（1）和式（2）求出每个基站覆盖范围内RSRP=-105 dBm 的点到基站的距离，作为基站的覆盖半径。

1.2 数学建模

基于以上基站选址的原则，本文把多目标的基站选址问题分解为3 个子目标：成本函数fcost、覆盖函数fcover和重叠覆盖函数foverlap，并将覆盖率作为约束条件。

假设实验区域长度为a，宽度为b，候选基站站址集合为BS={1，2，…，n}，测试点集合为test={1，2，…，m} 。候选基站被选中的情况可用表示，即：

第一个目标函数是成本函数，与基站个数有关。由于一般选取适应度较大的解作为优势解，因此转化成求解最大值，故做如下定义：

式中，distij表示基站i到测试点j的距离，Ri表示基站i的覆盖半径。

第二个目标函数是覆盖率，其值等于基站覆盖的测试点个数/测试点总数，由式（5）推出，即：

由于基站的重叠面积计算较为复杂，纯数学方法难以求解，故本文采用蒙特卡洛方法，首先建立起概率模型和待求解问题的联系，将点的概率等效为面积的概率；然后采用计算机技术在区域内随机抽取n′个试验点（本文设为2000）；最后借助统计规律求出基站重叠覆盖面积。

衡量试验点是否被重叠覆盖可用式（7）表示：

由式（7）可以推出区域重叠面积，即：

选中的基站覆盖总面积如式（9）：

第三个目标函数是重叠覆盖函数，可由式（7）～式（9）推出，为了使优化方向一致，转换为求解最大值问题，即：

本文采用权重法将多目标优化问题转化为单目标优化问题，建立的数学模型如下：

式中，ε表示覆盖率阈值，本文设为0.95。α、β和γ分别表示各个目标函数的权重系数，并且α+β+γ=1，这使得f（x）∈［0，1］。f（x）越大，越接近最优值。

2 改进多元宇宙优化算法在基站选址中的应用

2.1 二进制多元宇宙优化算法

MVO 算法［20］中每个宇宙代表优化问题的一个可行解，宇宙的膨胀率代表解的适应度值，通过模拟黑洞、白洞和虫洞的互相作用，寻找最优宇宙。算法描述如下：

式中，N为宇宙个数，D为宇宙维度，为第i个宇宙的第j个分量。

式中，为第k个宇宙（即白洞）的第j个分量；NI（x）i为第i个宇宙的归一化膨胀率。r1为［0，1］之间的随机数。

宇宙位置更新方式为：

式中，X（j）为全局最优宇宙的第j个分量；ubj和lbj分别为变量的上下界；r2、r3和r4都是［0，1］之间的随机数。WEP 表示虫洞存在率，TDR 表示旅行距离率，更新公式为：

式中，WEPmin和WEPmax为WEP 的最小值和最大值；t和T为当前和最大迭代次数；p为开采准确度。

基本MVO 算法仅适用于连续域，因此本文采用V型函数将实数映射到［0，1］区间，即：

最后进行位置更新：

本文将基本二进制多元宇宙优化算法简称为BMVO算法。

2.2 改进二进制多元宇宙优化算法

针对BMVO算法存在的早熟收敛、后期局部搜索能力弱等缺点，对BMVO 算法进行改进，提出离散禁忌-多元宇宙优化算法（TS-BMVO）。改进如下：1）借鉴其他智能优化算法［21-22］改进TDR 以均衡算法的全局和局部搜索能力；2）引进禁忌搜索算法抑制算法早熟收敛。

2.2.1 改进旅行距离率TDR

在BMVO算法中，算法能够在迭代前期依靠积累的经验迅速收敛到最优解附近，但是由于p值固定导致TDR 下降缓慢，算法后期局部搜索精度和能力较弱。因此，针对算法中存在的问题，本文采取动态p值，即：

改进前后的TDR 随p值的变化如图1 所示，经过改进TDR之后，算法在迭代前期迅速下降，依靠前期积累的经验迅速向最优宇宙移动，而从迭代总次数的1/3处开始，TDR下降的幅度趋于稳定，有利于后期深度局部搜索。相较于原始算法，减小了旅行距离，能够有效提升算法中后期搜索最优宇宙的精度与效率。

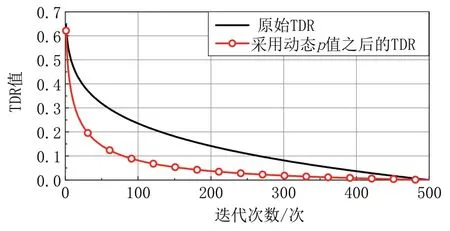
图1 TDR变化曲线对比图

仅仅用迭代次数决定算法收敛方向是片面的，故将TDR作进一步改进：

式中，fmean表示第t次迭代所有宇宙适应度值的均值。对于适应度值优于平均水平的宇宙，其对应的TDR值较小，不发生明显位置变化，有利于宇宙在旅行范围内进行深度局部开发；反之，对于性能较差的宇宙，其对应的TDR 较大，扩大搜索空间，快速向最优宇宙靠拢。本文将仅改进TDR 的MVO 算法称为TBMVO算法。

2.2.2 引进禁忌搜索算法

由于MVO 算法局部搜索能力有所不足，而禁忌搜索算法（Tabu Search，TS）［23］具有独特的“记忆功能”，局部寻优能力较强，因此引进TS 算法。在MVO算法寻优过程中，当检测到算法搜索能力较差时，将某次迭代中性能最差的解作为TS算法的初始解进行邻域搜索，并且设置禁忌表来禁忌最近若干次找到的局部最优解。当禁忌表达到容量上限时，按先后顺序依次释放禁忌对象。

邻域解采取2 点变异的方式，即随机选取当前解中2 个位置上的值进行“取反”操作，即0 变成1，1 变成0。

TS算法的流程如图2所示。

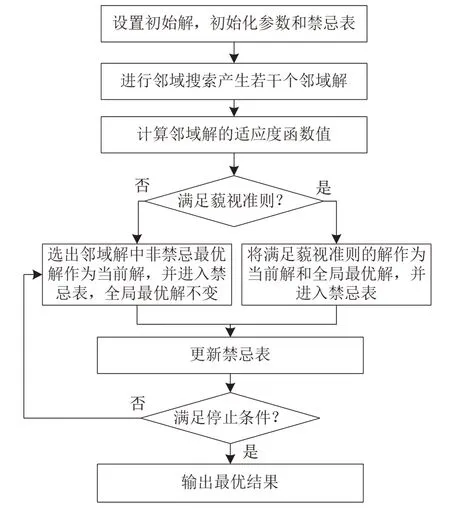
图2 禁忌搜索算法流程图

2.2.3 TS-BMVO算法

TS-BMVO 算法的总体流程如图3（a）所示，虚线框部分是本文算法的重点，分为2个步骤：

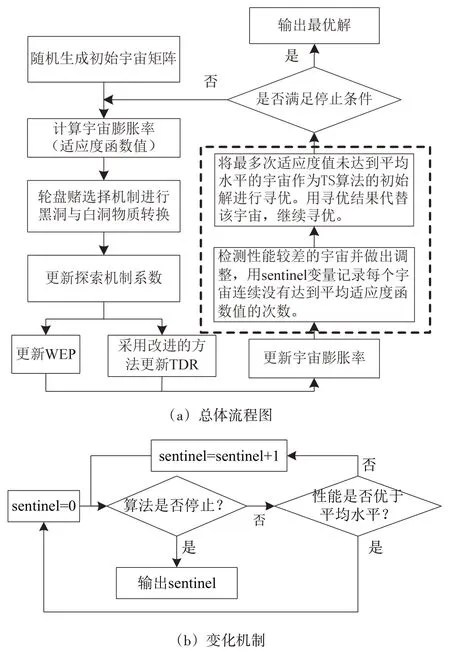
图3 TS-BMVO算法流程图

1）建立哨兵检测机制，辅助算法及时发现性能较差的宇宙，通过设置sentinel 变量实时记录各宇宙的性能没有超过平均水平的连续次数，其原理如图3（b）所示。若某次迭代中宇宙的适应度值超过平均水平，则对应的sentinel 值清零，直至算法结束停止sentinel 更新。迭代若干次后，认为sentinel 值最大的宇宙最有可能陷入局部最优，将该宇宙作为TS 算法的初始解。

2）运用TS算法求解优化问题，其最优解将代替上述性能较差的宇宙，继续搜索全局最优解，直至结束。

3 实验与结果分析

本文选取某5 km×5 km城市区域，采用上述基站选址问题的测试算例，分别运用BMVO 算法、TBMVO算法和TS-BMVO算法这3种不同算法进行仿真实验。同时，在相同模型下利用基本离散粒子群算法（BPSO）进行仿真实验，并与上面3 种算法进行比较分析。在基站选址问题的测试算例中，候选基站个数为65，测试点个数为170，基站覆盖半径为1.2909 km。

实验平台为：Windows10，Matlab R2021a。实验参数设置为：解的数量N为300，最大迭代次数Max-Iter 为500，均采用二进制编码。本文参考文献［24］的因素重要性比较结果，结合本文研究内容，在满足95%的覆盖阈值的前提下，以节约成本为第一优化目标，覆盖和重叠覆盖为其次，最后设置目标函数中的α为0.65、β为0.2、γ为0.15。

表1 比较了各个算法的适应度值、收敛代数、需要的基站个数、覆盖率、重叠覆盖面积。图4～图7 是仿真得到的基站分布图。其中蓝色点代表测试点；黑色空心圆圈为未被选中的基站，红色实心圆圈为被选中的基站。

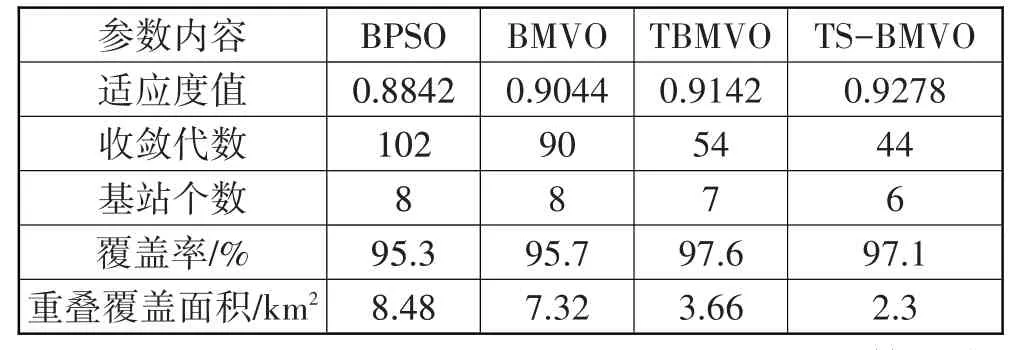
表1 各个算法的寻优结果

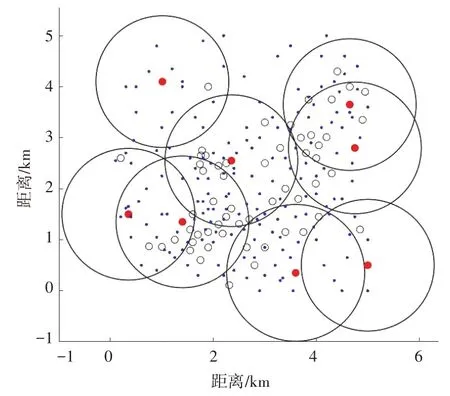
图4 基于BPSO算法仿真得到的基站分布图

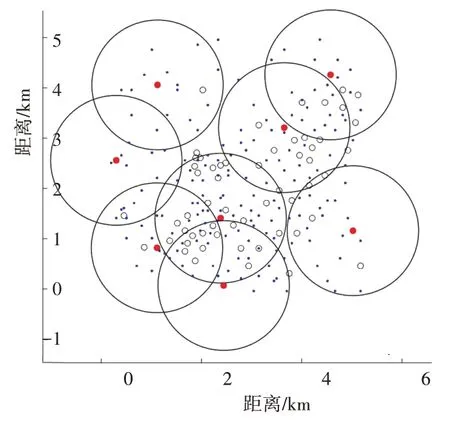
图5 基于BMVO算法仿真得到的基站分布图

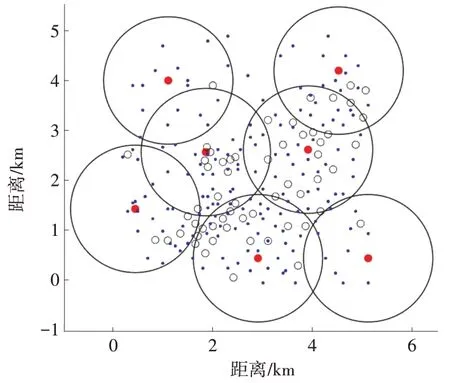
图6 基于TBMVO算法仿真得到的基站分布图

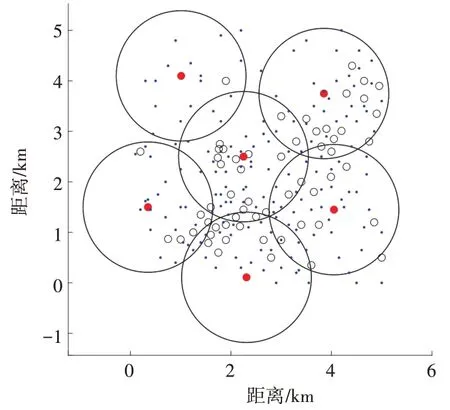
图7 基于TS-BMVO算法仿真得到的基站分布图

由图4～图7 和表1 可以看出，TS-BMVO 算法优化之后的建站数量和重叠覆盖面积明显优于另外3个算法；虽然覆盖率稍低于TBMVO 算法，但是TBMVO 算法覆盖率高的代价是建站成本增加，并不满足电力无线专网长期可持续发展的原则，而TSBMVO 算法能够在满足覆盖率阈值的前提下兼顾电网经济性原则，抑制同频干扰的效果更好，且未来可用于成本较低的中继站或者微站补充覆盖。因此本文提出的TS-BMVO 算法可以运用到基站选址问题中，在最小成本的前提下，获得最优的网络质量。

各个算法的适应度函数变化曲线如图8 所示。由图8 可以看出：1）在迭代前期TS-BMVO 算法的适应度值迅速增加，并且持续高于另外3个算法；2）TSBMVO 算法明显具有优越的收敛性能。这是因为本文通过改进TDR 很好地平衡了算法迭代前后期的收敛过程，又引进了TS算法，避免了算法无意义的迂回搜索。综上，本文提出的TS-BMVO 算法的全局搜索能力较强。

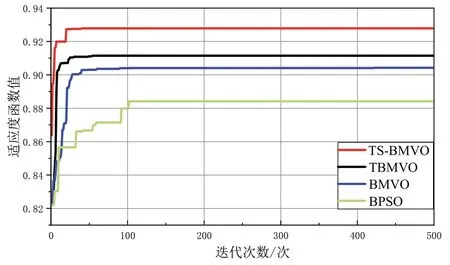
图8 各个算法的适应度函数曲线图

4 结束语

本文根据TD-LTE 电力无线专网当前实际需求，确定了基站选址的主要目标，基于此，构建了基站选址优化的数学模型，并采用改进的MVO 算法进行求解。主要对MVO 算法进行了2 点改进：1）改进TDR参数；2）融入禁忌搜索算法。仿真结果表明TSBMVO 算法具有优越的性能，在满足电网的基站规划特征和覆盖率要求的同时，能够以最少的投资预算获得最大的经济效益，并且有效保证了终端信号质量。