基于改进D3QN算法的泊车机器人路径规划

王健铭，王 欣，李养辉，王殿龙

（1.大连理工大学机械工程学院，辽宁 大连 116023；2.大连船舶重工集团有限公司生产保障部，辽宁 大连 116023）

0 引 言

为解决泊车难的问题，泊车机器人应运而生。自2014年第一台Ray自动泊车机器人横空出世以来，许多企业推出了不同类型的泊车机器人，如深圳怡丰国内首创的梳齿型停车AGV 和车抬板停车AGV，海康威视应用视觉和惯性双导航技术的“阡陌”泊车机器人［1］。目前泊车机器人技术已进入快速发展阶段，而路径规划是泊车机器人的重要技术支撑。

目前泊车机器人多是以A*及其改进算法为主，存在规划效率不高、规划路径长及冗余点多和难以适应环境的改变等问题。在其所属的移动机器人领域中，路径规划算法已逐步从人工势场法［2］、A*算法［3］、Dijkstra 算法［4］等，向智能仿生算法发展，如模拟退火法［5］、遗传算法［6］、神经网络算法［7］和蚁群算法［8］等。但智能仿真算法在状态空间复杂的环境下计算量大、效率低，不易保证路径规划的实时性。进而，许多学者又引入了深度强化学习（Deep Reinforcement Learning，DRL）算法［9］。该算法是深度学习（Deep Learning，DL）［10］与强化学习（Reinforcement Learning，RL）［11］的结合，利用神经网络提取特征信息并获得机器人所需环境信息，实现状态动作值函数的拟合和状态到动作的映射。它充分发挥了深度学习的感知能力和强化学习的决策能力，有效解决了移动机器人的路径规划问题。

在此基础上，Google 的DeepMind 团队首次提出将传统RL 中的Q-Learning 算法与卷积神经网络结合，称其为深度Q 网络（Deep Q-Network，DQN），并在Atari 2600 游戏上有很好的表现［12］。但在动态复杂未知环境中，DQN 算法存在收敛速度慢、过估计的问题，导致最终规划出的路径并非最优解。为此，Hasselt等［13］提出了一种深度双Q网络（Double DQN，DDQN）使智能体能够选择出Q值最大的动作，从而解决了DQN 算法存在的过估计问题。Wang 等［14］提出了一种竞争深度Q 网络（Dueling DQN），通过优化网络结构提高了网络的收敛速度。Tai 等［15］首次采用DQN 算法解决移动机器人路径规划问题。董瑶等［16］提出了一种改进的基于深度竞争网络结构的双Q 网络方法，用来改善机器人路径规划时收敛速度慢的情况。董永峰等［17］为解决机器人路径规划中的过估计问题，提出了一种动态融合深度双Q算法。成怡等［18］采取改进奖惩函数、优化状态空间的方法以解决奖励稀疏和探索能力差问题。

近年来，深度强化学习算法被广泛用于移动机器人技术中。邓悟［19］基于多智能体DRL框架MADDPG提出了一种可用于双智能体的路径规划算法，可在导航中同时处理每个智能体的任务需求。Lima 等［20］通过模拟车辆轨迹将DRL 用于路径规划任务中，使车辆的运动更安全且路径更短。Bartolomei 等［21］提出了一种结合语义感知技术的无人机路径规划方法，利用深度强化学习实现复杂环境下基于视觉的导航。

由此可以看出，在DQN 算法基础上发展的深度强化学习算法在路径规划方面具有很好的表现。而本文的研究对象为差速运动的泊车机器人，其状态和动作空间是离散的，具有3 个动作，因此适合采用改进的DQN 算法进行路径规划。为提高路径规划效率，适应未知环境场景，本文在D3QN 的基础上，改进网络结构，修改奖惩机制，增加优秀动作判定，提出一种SE-RD3QN（Squeeze-and-Excitation Residual D3QN）路径规划算法，并应用于泊车机器人路径规划中，最终通过实验验证SE-RD3QN 算法的优异性和实用性。

1 D3QN算法原理

D3QN（Dueling Double DQN）算法［22］是在Dueling DQN 算法的基础上融入了Doubel DQN 算法的思想，它在目标值的计算方式上较Dueling DQN 算法有所改进，可以有效解决算法由于对期望值Q值的过估计而导致未能选择最优动作的问题。

D3QN 算法网络结构如图1 所示，由卷积层和全连接层组成。卷积层提取输入数据的目标特征，然后送入全连接层。全连接层为竞争网络结构，分为优势函数网络A（s，a；β，θ）和价值函数网络V（s；α，θ）。其中优势函数与智能体的状态和动作都有关，而价值函数只与状态有关。最后组合输出累计折扣奖励的期望值Q值，即：

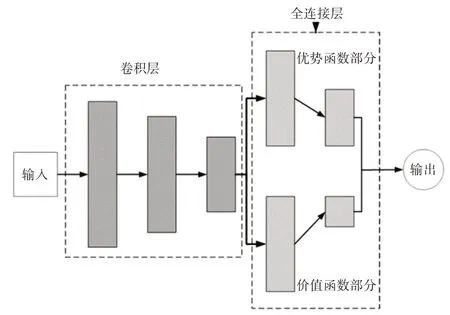
图1 D3QN网络结构

式中，s表示状态，a表示动作，α是价值函数支路的网络参数，β是优势函数支路的网络参数，θ为公共部分的网络参数。

D3QN 算法使用2个具有相同结构和初始参数的网络，即估计网络和目标网络。状态动作值函数用估计网络计算，目标值函数用目标网络计算，通过经验回放机制有效利用历史数据，有利于算法的收敛。

D3QN 算法使用ε-greedy 策略选择智能体的动作，可兼顾探索和利用。该算法利用估计网络获取与St+1状态中最大Q值对应的动作amax，即：

然后根据所选动作计算出目标网络中的目标Q值，即：

D3QN的损失函数为：

式中，Q（st+1，amax；θ-）和Q（s，a；θ）分别为目标网络和估计网络的值函数。

2 SE-RD3QN改进算法

D3QN 算法在实际训练任务中通常采用深度神经网络结构。随着网络深度的加深，会产生网络退化和卷积层时间复杂度迅速增加的现象。网络加深后，深层网络模型的效果理论上不会低于浅层网络，但事实上，如果直接使用普通深层网络，效果反而会比浅层网络更差。卷积层时间复杂度的迅速增加，会对硬件提出更高要求，这意味着深度模型的训练比浅层模型更难。为解决此问题，本文改进卷积层网络为残差网络，并引入注意力机制，进而提出SE-RD3QN算法。

2.1 残差网络结构

针对网络退化现象，在D3QN 算法的基础上，将传统卷积网络改为残差网络ResNet（Residual Network）［23］，并嵌入SE 注意力模块（Squeeze-and-Excitation Block）［24］，构成SE-ResNet网络。

与卷积网络对比，如图2 所示，ResNet 直接连接并组合了不同深度的卷积层的输出，在深化卷积神经网络的同时控制了网络的复杂度；还通过短路机制增加了1个剩余单元，并在网络旁边打开1个通道，以便输入可以直接到达输出。优化的目标由原来的拟合输出F（x）变为输出与残差路径输入x之和，即H（x）=F（x）+x。这样，可防止模型训练过程中，由于网络深度过深而丢失从前一层提取的特征信息。因此，使用ResNet在保持网络深度和复杂度的条件下，避免了传统卷积神经网络因深度过深可能导致梯度消失和退化的问题，简化了学习目标，更利于网络收敛。

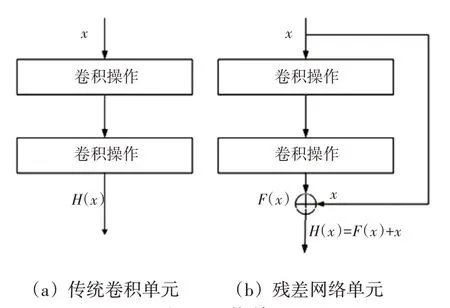
图2 网络单元

2.2 注意力机制

注意力机制（Attention Mechanism）是一种学习思想，源于生物视觉中的大脑信号处理过程，通过特征值提取、注意力计算等步骤，提高系统对象的学习性能，SE模块是注意力机制模块的一种。

一般情况下，在对深度卷积神经网络全连接层的最终输出进行维度转换后，得到的特征信息会有一定程度的丢失，因此，本文将SE 模块嵌入在残差网络中，如图3 所示。SE 注意力模块全称为“挤压-激励”块，是一种基于通道注意力机制的深度学习模型，包含Squeeze（压缩）和Excitation（激励）这2 个部分，以通道为单位的特征响应可以通过明确地对通道之间的相互依赖关系进行建模来适应性地重新校准，增强有用特征信息并压缩无效特征信息，提高模型中各个通道特征的辨识力，理论上有助于选择最优路径。

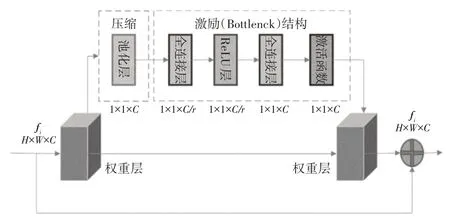
图3 SE-ResNet结构

通道注意力机制可以让模型自动学习输入特征中每个通道的重要性，从而提高模型的性能。SE 模块在压缩结构下，通过全局池化层的压缩操作，将ResNet 最后的全连接层输出的H×W×C（空间维度）的特征映射fi进行压缩。在激励结构下，通过瓶颈结构（Bottleneck）的激励操作，进行全局学习获得每个特征通道的作用程度，并根据学习到的注意力权重为相应的特征通道赋值，最后输出带有注意力标注的H×W×C特征映射f′i。通道注意力机制的具体实现方式如式（5）和式（6）所示，W1与W0表示2层全连接层操作，表示经池化层压缩后的1维通道特征，Fi为输入特征映射，Fc表示输出通道特征，Wc表示权重参数，是1×1×C维的向量，每一维的数对应该通道的权重，σ表示Sigmoid 激活函数，用于将输入值映射到0到1之间的概率值。

2.3 SE-RD3QN算法网络结构与流程

SE-RD3QN 算法网络结构如图4 所示，输入层为机器人当前状态，如式（7）所示，是一个包含激光雷达16个角度的距离参数的向量，经过SE-ResNet模块传递给全连接层，其中256@3×3 代表该卷积层输出通道为256、卷积核的大小为3×3。

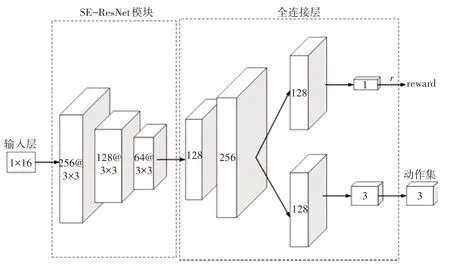
图4 SE-RD3QN网络结构

SE-ResNet模块是一个具有3个卷积层的网络结构，每个卷积层都包含卷积、批量归一化、ReLU 激活函数和最大池化操作。每2 个卷积层之间连接一层包含2个残差块的SE残差层，每个残差块包含2个卷积层、批量归一化、ReLU 激活函数和SE 模块。SE 模块包含全局平均池化层、2 个全连接层、ReLU 激活函数和Sigmoid 激活函数。其中，ReLU 函数可以增强深度学习模型的非线性表达能力，最大池化操作可以减少参数数量，从而提高深度学习模型的效率和泛化能力。SE-ResNet网络结构如图5所示。

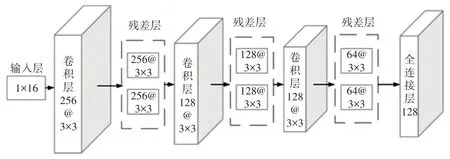
图5 SE-ResNet网络结构

如图6所示，SE模块位于残差模块卷积操作与求和操作之间，它的作用是在前向传播过程中自适应地调整输入特征的权重，在第一个残差层中，SE 模块的2 个全连接层维度分别为32×256 和256×32，在第二残差层中为16×128 和128×16，在第三个残差层中为8×64 和64×8，通过2 个全连接层的升维和降维处理，最后使用Sigmoid函数将特征归一化得到每个通道的权重。这样，网络就可以自动地学习和提取每个通道中最为重要的特征，从而提高网络的表达能力和泛化能力。

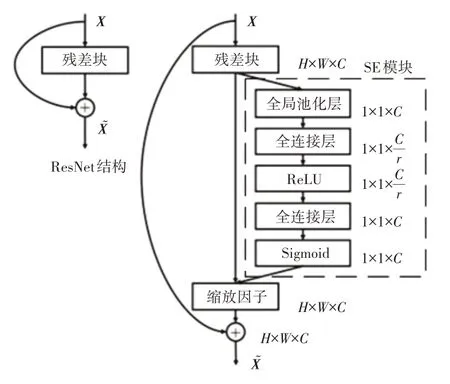
图6 SE-ResNet网络单元

全连接层将输入均分为2 个部分，一部分作为价值函数网络的输入，其输出状态值与奖励值经过加权求和后作为输出，另一部分作为优势函数网络的输入，其输出为状态动作Q值。通过选择最大Q值的动作，并将其和价值函数的输出结果相加，从而得到最终的输出结果。

SE-RD3QN 算法的路径规划流程如图7 所示，将采集的距离参数传入到估计网络中提取环境特征，得到机器人的当前状态St输入至目标网络，计算出Q值选择当前动作a，并根据获取的奖励值r评估该动作的好坏。机器人进入到下一状态，并将与环境交互所获取的样本s、a、r、st+1存储到经验回访池中，通过随机采样进行采样训练，根据估计网络和目标网络的输出A（st，a；θ）和ytarget计算出损失函数，然后进行反向传播来循环迭代更新网络参数，直至训练完成。经过不断循环以上过程，以累积奖励值Reward 最大为目标，最终得到最优动作值函数A*（st+1，a；θ-）所对应的最优动作。SE-RD3QN算法流程如下：

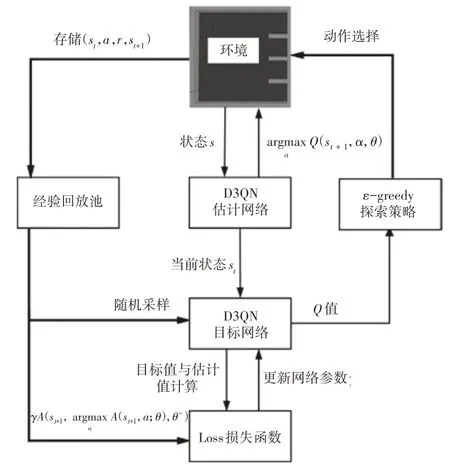
图7 路径规划流程图

3 仿真实验结果及分析

本文通过搭建仿真环境分别对D3QN、增加残差层的RD3QN算法和本文提出的SE-RD3QN算法进行训练，验证残差层和注意力模块对模型训练效果的改善，通过对比Loss曲线验证改进结构的有效性，并根据Loss曲线和Reward曲线验证改进奖惩机制的有效性。

3.1 仿真平台的搭建

泊车环境和泊车机器人模型在Gazebo 软件下建立。本文实验的操作系统为ROS 机器人操作系统，考虑与ROS 的兼容性问题，选择可进行三维机器人运动学和动力学仿真的Gazebo 软件来进行路径规划实验训练，该软件可精准地模拟出复杂环境下传感器的作用及机器人的动态［25］。

在Gazebo 软件中建立的仿真环境与泊车机器人模型如图8所示。其中泊车环境为2.6 m×2.6 m的封闭空间，包含右侧4个0.5 m×0.5 m的停车位，图中机器人的位置即是起点，仿真过程默认已经将汽车放到机器人上方。机器人尺寸为0.3 m×0.2 m×0.11 m，车轮半径为0.0325 m、宽为0.026 m，轮距为0.226 m。机器人采用四驱差速运动控制，具有前进、左转和右转3个动作。

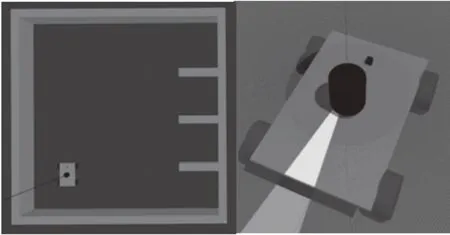
图8 仿真环境和机器人模型

在仿真环境中，泊车机器人需要从起始点通过自主路径规划与导航到达目标停车位，过程中需要不断依靠传感器与环境进行交互，获取所需的环境信息。本文中泊车机器人采用激光雷达传感器来感知环境信息，并选用IMU（惯性传感器）和里程计，分别获取机器人实时线速度、角速度、角加速度和位置信息。

强化学习算法应用OpenAI Gym 工具包［26］来开发和调试。应用该工具包构建SE-RD3QN 算法来训练机器人，再应用openai_ros功能包将ROS、Gazebo与OpenAI Gym 三者联合，来完成对机器人的训练任务。其中ROS 提供硬件驱动、动力学模拟、环境感知和控制器编程等功能，Gazebo 提供多模拟器、物理引擎和可视化系统，而OpenAI Gym 则提供模拟环境和游戏引擎，以及用于训练机器学习模型的接口。三者的联合使用可以模拟复杂的机器人和智能体行为，从而为机器人和智能体的训练提供强大的支持。

Gazebo 软件与OpenAI Gym 工具包之间的通信通过创建节点和话题来实现。在ROS 中，节点是最小的进程单元，通常一个节点负责控制机器人某个功能，节点和节点之间依靠话题进行通讯。泊车机器人在仿真时，其必要的ROS节点关系图如图9所示。

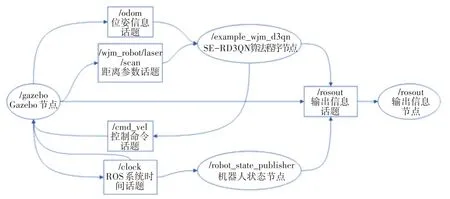
图9 ROS节点关系图

3.2 模型训练

泊车机器人在仿真环境中训练时角速度恒为1.0 rad/s，其环境状态s∈S、动作空间a∈A，定义机器人的动作空间为：

其中每个动作对应的名称及线速度如表1 所示，根据SE-RD3QN算法得到每个动作对应的一个Q值，然后选择最大的Q值所对应的动作执行。

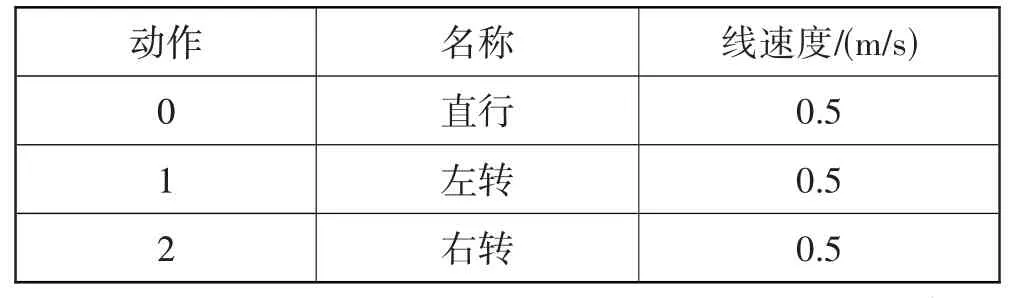
表1 泊车机器人训练时速度

环境状态列表S如表2所示，其中，激光雷达参数作为神经网络的输入状态，而将机器人位置信息和距离目标点的距离作为环境状态列表的一部分，在训练过程中进行监测和记录，以便路径规划算法对环境进行搜索和判断，从而找到最佳路径。

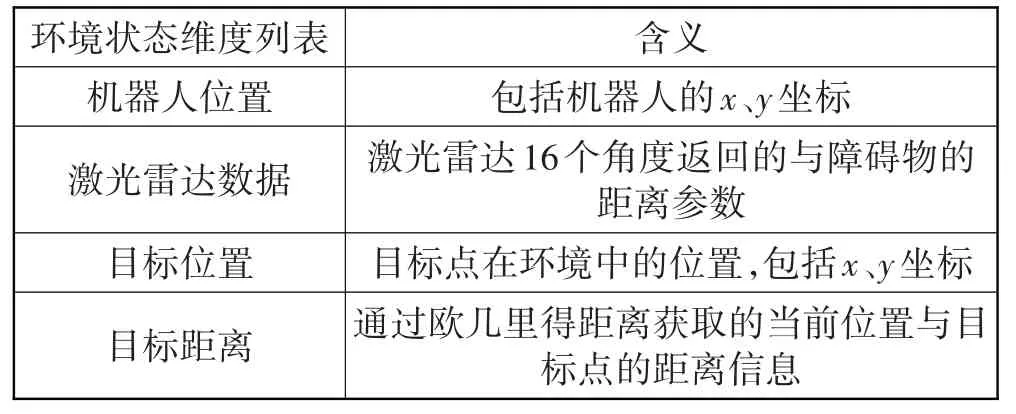
表2 环境状态列表

SE-RD3QN 算法的神经网络超参数设置如表3所示。其中探索率ε 会逐渐衰减，计算公式如式（9）所示。为了促进算法的收敛，本文使用CyclicLR 循环学习率，其学习率可进行周期性变换，即：

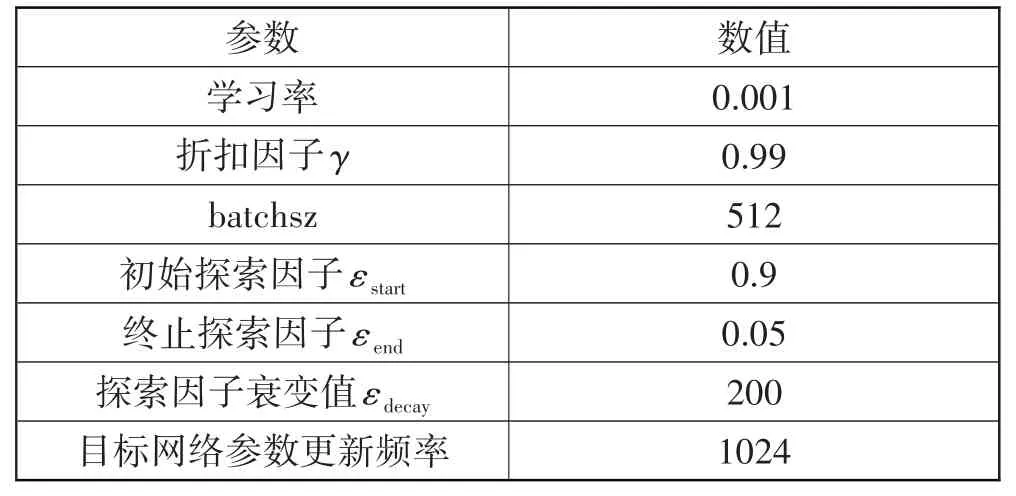
表3 神经网络超参数

为提高SE-RD3QN 算法的训练速度，训练时仅提取激光雷达采集到的0°～360°数据列表中的16 个角度值，代表机器人与障碍物的距离。这些值与最小距离参数进行比较，以检测机器人是否与环境中的障碍物碰撞。泊车机器人的动作奖励值列于表4 中。碰撞会导致机器人获得-120 的奖励值，并返回起点重新开始。到达目标点时，机器人将获得奖励值240。本文通过修改算法超参数和优化奖惩机制，不断训练，以使损失函数曲线（Loss）平稳下降并尽快收敛，同时获得最大的奖励值（Reward）。

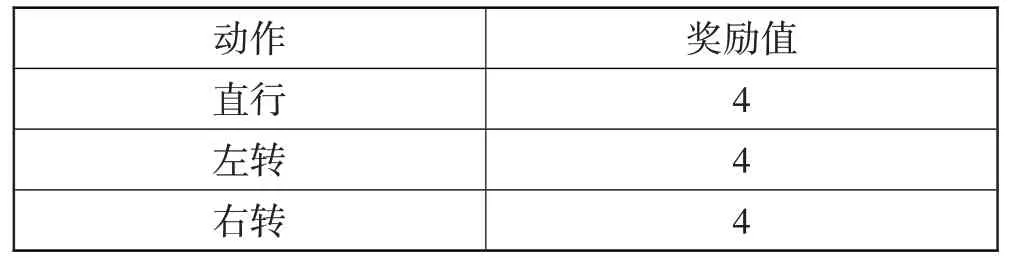
表4 奖励值设置

一般算法的训练效果可通过收敛速度和累积奖励值2 项指标来体现。收敛速度反映学习能力，收敛速度越快，则机器人在更少迭代次数下学习能力越好；累积奖励值反映学习效果，累积奖励值越多，则机器人训练时到达目标点的次数越多，训练效果越好。

为了验证残差层和注意力模块对模型训练效果的改善，在仿真环境中分别对D3QN 算法、增加残差层的RD3QN 算法和SE-RD3QN 算法进行训练，神经网络超参数设置见表3。比较3种算法的损失曲线如图10 所示，DQN 算法在3800 步左右Loss 值突然上升，发生了网络退化现象；RD3QN 算法解决了网络退化问题，并且算法收敛速度较D3QN 算法明显提升，Loss 最小值小于D3QN；SE-RD3QN 算法的收敛速度进一步提升，且Loss 最小值在3 种算法中最低，说明本算法在相同用时能够实现更好的性能，并且对数据集的拟合效果更好。

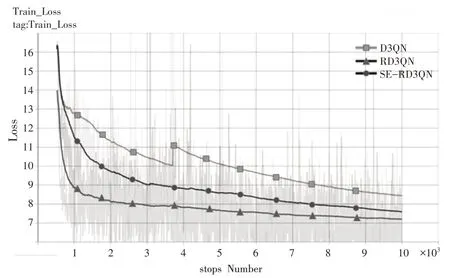
图10 D3QN、RD3QN、SE-RD3QN算法Loss曲线

SE-RD3QN 算法的网络性能如表5 所示，相比D3QN 算法拥有更多的模型参数量和更长的单集运行时间，但是在实验中，SE-RD3QN 算法首次找到目标点的步数显著减少，从1127步减少到了432步。这说明SE-RD3QN 算法在解决复杂问题时具有更强的搜索能力和学习能力，能够更快找到最优解。因此，SE-RD3QN算法具有更高的可行性和优势，可以作为一种有效的强化学习算法来解决复杂问题。仿真实验训练过程中使用的硬件配置中，CPU 的型号为Intel Core i7-10870H，图形处理器GPU 为NVIDIA Ge-Force GTX1650Ti。

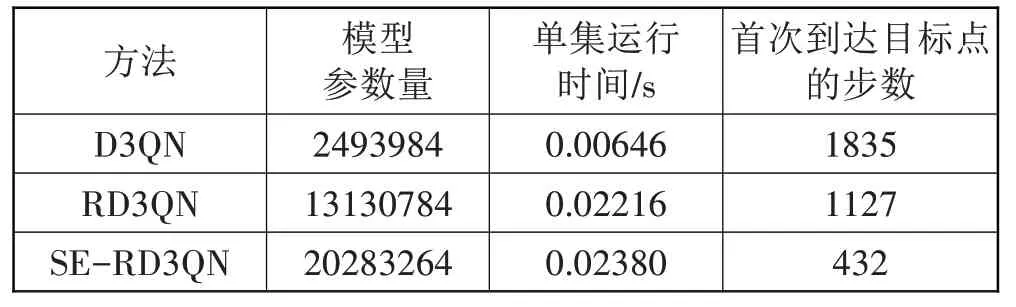
表5 D3QN、RD3QN、SE-RD3QN算法性能

奖惩机制对训练效果有显著影响。为了缩短机器人到达目标点的时间，本文改进了奖励机制。优化前，机器人采取直行或转向动作时获得相应奖励，到达目标点时获得终极奖励，碰撞则扣除一半终极奖励。优化后，在此基础上增加了有效步、无效步和更优步的判定。机器人采取直行或转向动作时，获得相应奖励并进行判定。若自身与目标点的绝对距离小于上个位置的绝对距离，则视为有效步并再次获得相应奖励；反之为无效步，不获得奖励，若绝对距离的缩减量超过步长的一半，则获得2 倍的动作奖励。优化后的奖励机制可使机器人更快到达目标点且获得更大奖励，有助于路径规划训练。

为了进一步验证SE-RD3QN 算法的训练效果，将其Loss曲线和Reward曲线与D3QN算法对比，并增加有无奖惩机制的对比实验，将应用奖惩机制的SERD3QN算法和D3QN算法命名为SE-RD3QN′算法和D3QN′算法，验证改进奖惩机制的有效性。将算法训练后得到的损失函数曲线（Loss）如图11所示，结果表明：SE-RD3QN 算法Loss 曲线在2000 步左右处开始收敛，收敛速度较快，而D3QN算法在9000步左右开始收敛，收敛速度较慢，而D3QN′算法收敛速度有了明显的提升，在5000 步左便开始收敛，而SE-RD3QN′算法收敛速度并未明显改变。这表明SE-RD3QN 算法解决了网络退化问题，并提高了学习能力，已具有较好的收敛速度，因此再应用优化的奖惩机制提升的进一步收敛速度没有D3QN′算法表现得那么明显。

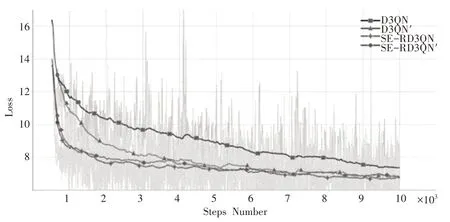
图11 D3QN、D3QN′、SE-RD3QN、SE-RD3QN′算法Loss曲线

4 种算法的奖励值曲线对比如图12 和表6 所示，可以看出SE-RD3QN 算法每一步的奖励值都在D3QN 算法之上，并在使用优化奖惩机制后有了更明显的提升。SE-RD3QN 算法的平均奖励值为2.854，比D3QN算法的1.812高出了57.5%，而优化了奖惩机制的SE-RD3QN′算法为3.785 比原算法高出32.6%，说明在躲避障碍物上和动作选择方面，SE-RD3QN比D3QN 算法更有优势，优化的奖惩机制作用效果也十分显著。

表6 平均奖励值对比

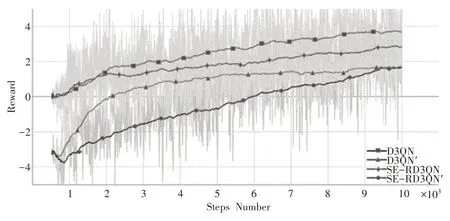
图12 D3QN、D3QN′、SE-RD3QN、SE-RD3QN′算法Reward曲线

4 算例分析

为进一步体现本文方法在泊车机器人路径规划上的优势，这里与目前常用的A*+TEB 算法进行对比。其中A*算法用于全局路径规划，TEB［27］算法用于局部路径规划，并在差速运动机器人的路径规划上表现较好。对比的2 种算法设置相同的起点和目标点，仿真过程如图13和图14所示。

图13 应用SE-RD3QN算法仿真过程

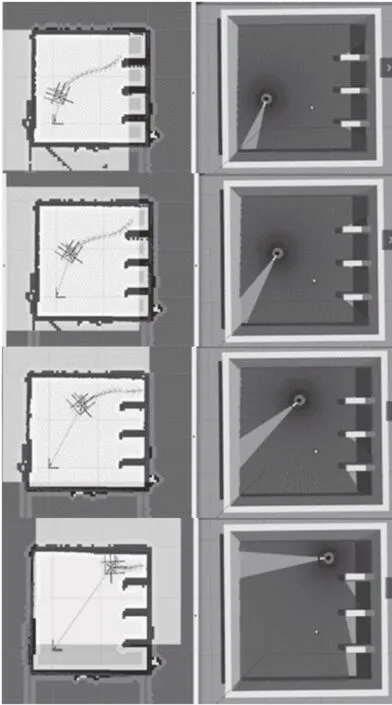
图14 应用A*+TEB算法仿真过程

对比泊车机器人从起点到目标点花费的时间、规划路径的长度和路径的平滑程度，如图15和表7所示，可以明显看出SE-RD3QN 算法获得轨迹曲线更加连贯平稳，运动轨迹更加平滑；而A*+TEB算法获得轨迹曲线有转折，轨迹冗余点较多且拐点多，表明运动存在骤行骤停，转向与前进结合自如性较差。SE-RD3QN算法获得的路径略短于A*+TEB 算法，而规划时间仅是A*+TEB 算法的1/2，具有明显的优势。A*+TEB 算法的规划时间更多花费在转弯处的计算量上，因此难以适用于环境复杂、计算维度高的路径规划中。

表7 不同算法规划的路径

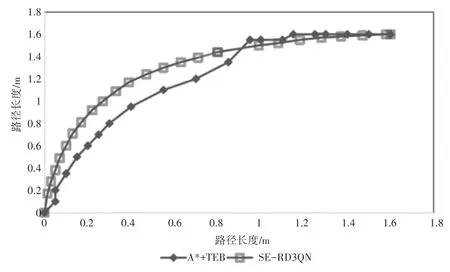
图15 路径轨迹曲线

为了验证训练的网络模型在真实环境中的实用性，如图16 所示，建立与仿真环境等比例缩放的真实场景（见图16（a））以四轮小车代替泊车机器人（见图16（b））。此小车由四驱差速底盘、stm32单片机、树莓派4b以及激光雷达等硬件组成，上位机主机为树莓派，安装有Ubuntu MATE 操作系统和ROS Melodic，下位机从机为笔记本电脑（PC），安装有Ubuntu18.04 和ROS Melodic，PC端通过SSH协议远程控制四轮小车。

图16 实验场景与机器人实验平台

将SE-RD3QN 算法在仿真环境中训练得到的网络模型移植到四轮小车上，其路径规划的实验截图如图17 所示，图中对应位置的激光雷达数据如图18 所示，小车可以在未知环境中感知环境状态，并选择合适的动作达到目标状态，说明该模型可以实现实物小车的实时路径规划，表明该算法的有效性与实用性。

图17 四轮小车的路径规划实验截图

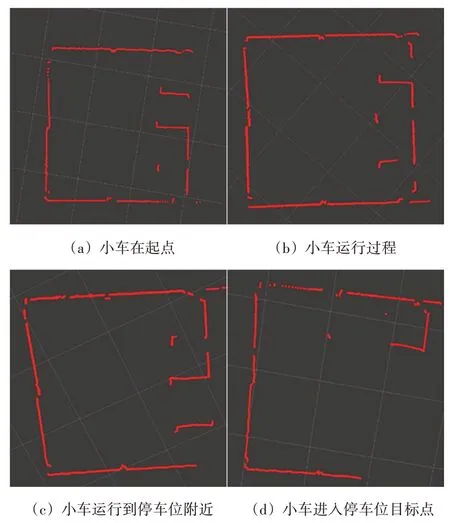
图18 Rviz中激光雷达信息

5 结束语

针对A*算法对泊车机器人路径规划时存在普适性差、不适用于复杂运动和复杂多变环境的问题，本文提出了SE-RD3QN 算法应用于该类型机器人的路径规划。该算法在D3QN 算法的基础上，将卷积网络修改为残差网络，嵌入注意力机制，改善了D3QN 算法存在的网络退化和收敛速度慢的问题，并结合优化的奖惩机制，进一步缩短了算法训练的时间，提高了路径规划决策能力。仿真实验表明，应用SE-RD3QN算法的泊车机器人在路径规划中的表现从路径的平滑程度、运行的平稳性、路径长度和规划时间等方面明显优于应用A*算法。最后将训练模型用于真实环境下的实验场景中，进一步验证了本文算法的训练效果。