基于永磁同步电机的滑模与自抗扰协调速度控制研究

张龙飞，毕栋，张友兵

摘要：为了解决永磁同步电机（permanent magnet synchronous motor，PMSM）矢量控制中采用指数滑模在调速控制时，出现的超调量大、抖振严重及抗干扰能力差等问题，采用滑模和降阶线性自抗扰的复合控制策略。通过一个可变的加权因子，使得滑模和降阶线性自抗扰在矢量控制系统的速度环中各占一定比重，所占比重的和为1。仿真结果表明，该控制策略对比指数滑模，在加减速、正反转时抖振显著减少，均实现无超调跟踪，并更快地收敛至参考速度；在加载和卸载时，抖振明显减少，超调量也分别减少了17%和18%。该策略不仅能有效改善控制系统的性能，对速度变化也具有較强的鲁棒性。

关键词：永磁同步电机；指数滑模；降阶线性自抗扰；复合控制

中图分类号：TM301.2                文献标志码：A

Research on coordinated speed control of sliding mode and active disturbance rejection based on permanent magnet synchronous motor

ZHANG Longfei， BI Dong， ZHANG Youbing

（School of Automotive Engineers， Hubei University of Automotive Technology， Shiyan 442002， China）

Abstract： In order to solve the problem of large overshoot， serious chattering and poor anti-interference ability when using exponential sliding mode in speed control of permanent magnet synchronous motor（PMSM） vector control， a composite control strategy of sliding mode and reduced-order linear active disturbance rejection was adopted. The strategy made the sliding mode and reduced-order linear active disturbance rejection occupy a certain proportion in the speed loop of the vector control system through a variable weighting factor， and ensured that the sum of their respective proportions was 1. The simulation results show that compared with the exponential sliding mode， the chattering of the control strategy is significantly reduced during acceleration and deceleration， or positive and negative inversion. Besides， no overshoot tracking is achieved， and it can converge to the reference speed faster. During loading and unloading， not only the chattering is significantly reduced， but also the overshoot is reduced by 17% and 18%， respectively. The strategy not only effectively improves the performance of the control system， but also has strong robustness to speed changes.

Key words： permanent magnet synchronous motor（PMSM）; exponential sliding mode; reduced-order linear active distrubance rejection; composite control

永磁同步电机（permanent magnet synchronous motor，PMSM）与普通的电励磁同步电机相比，电机结构更加简单，效率更高［1］。正因为存在诸多优点，越来越多的行业开始使用PMSM，如家用电器、冶金行业和石油行业等，同时也获得了各个车企的青睐[2] 。

滑模控制是常用的非线性控制[3] ，对系统模型具有很小的依赖性，重点是通过滑模面来实现控制，其核心是滑模面的设计。相比传统的比例——积分控制（proportion integration differentiation，PID）算法，滑模控制的优势有：对于系统的不确定性和干扰具有较强的鲁棒性，不依赖系统模型以及响应速度快[4] 。但是，滑模控制也存在劣势，如对系统噪声敏感和控制器设计复杂等[5]。

线性自抗扰控制（linear active disturbance rejection control，LADRC）是一种新型的控制算法[6]，其能够有效抵消系统内外部的干扰，具有较强的适应性[7] 。该算法不需要对系统进行精确建模，仅需要对系统进行初步的参数估计即可实现控制，因此，具有较强的实用性。相比传统的PID控制算法，LADRC算法的优势在于对系统内外部的扰动有很强的抵抗能力，并有较好的跟踪性能和较小的跟踪误差。因此，LADRC算法在工业控制、机器人控制和航空航天等领域具有广泛的应用前景[8-9] 。

综上，本文在研究滑模控制和自抗扰控制的基础上，设计了一种基于滑模与线性自抗扰复合控制的策略，主要实现对PMSM矢量控制速度的有效调节。在控制策略中，滑模控制主要负责系统的快速响应和快速收敛，而线性自抗扰控制则主要负责系统的稳定性和鲁棒性。通过不同加权因子的设置，可以实现滑模控制和线性自抗扰控制的不同权重组合，该策略不仅能提高控制系统的动态响应能力，而且还能够减缓滑模控制的抖振，在提高系统的稳定性和鲁棒性方面，具有较高的实用价值和应用前景。

1PMSM矢量控制

1.1数学模型

为了对PMSM进行更好地控制和分析，本文将PMSM模型理想化处理。通过坐标变换将其从三相静止坐标系转换为两相静止坐标系[10] ，再从两相静止坐标系变换到两相旋转坐标系，基于两相旋转坐标系d-q建立数学模型[11] ，构成的定子电压方程如下式[12] ：

ud=Rid+dψddt－ωeψquq=Riq+dψqdt+ωeψd（1）

定子磁链方程为

ψd=Ldid+ψfψq=Lqiq（2）

将式（2）代入式（1）中，可得定子电压方程为

ud=Rid+didLddt－ωeiqLquq=Riq+diqLqdt+ωe（idLd+ψf）（3）

式中：ud、 uq为定子电压在d-q轴分量；id、iq为定子电流d-q轴分量；R为定子电阻；ψd、ψq为定子磁链d-q轴分量；ωe为电角速度；Ld、Lq为d-q轴电感分量；ψf为永磁体磁链[13] 。

本文采用的PMSM为表贴式，d-q轴的电感大小一样，因此，电磁转矩方程为

Te=32pnψfiq（4）

运动方程为

Te－TL－Brωm=Jdωmdt（5）

式中：pn为极对数；Te为电磁转矩；TL为负载转矩；J为转动惯量；ωm为机械角速度；Br为摩擦因数。

1.2控制系统

矢量控制是目前应用最为广泛的控制策略之一，具有控制电流小和转矩控制性能好等特点。因此，经过多年的发展依然是控制领域研究的基础，众多学者并以此为基础，进行着大量的技术研究。

2复合控制器设计

2.1复合控制器的实现

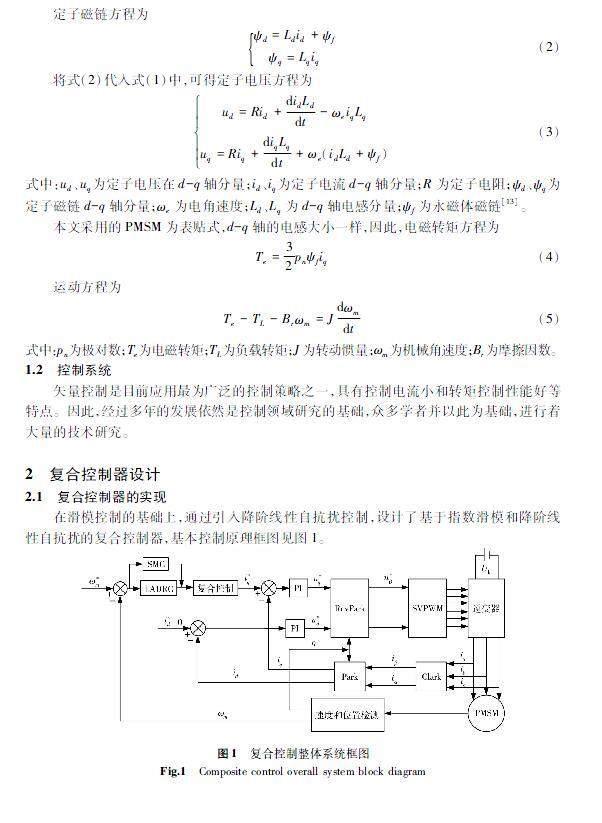
在滑模控制的基础上，通过引入降阶线性自抗扰控制，设计了基于指数滑模和降阶线性自抗扰的复合控制器，基本控制原理框图见图1。

该复合控制器通过调节加权因子α（0≤α≤1）将指数滑模控制和降阶线性自抗扰控制有效、协调地结合起来，其结构见图2。

采用滑模控制时，系统在滑模面时的抖振较大。且系统的抗干扰能力差，但系统的响应收敛能力较强。通过调节该复合控制器的加权因子α使控制器同时兼备滑模控制和降阶线性自抗扰控制两者的优点，使得系统不仅有更好的响应收敛能力，且抗干扰能力、稳定性和鲁棒性都显著增强。此外，当α=0或α=1时可实现两种控制策略的独立工作。

2.2滑模控制

滑模变结构控制的设计主要分为滑模面函数设计和趋近律设计。

1）滑模面函数设计

系统状态量为

x1=ω*m－ωmx2=－dωmdt（6）

求导得：

x1·=－ω·mx2·=－3pnψf2Jiq+BJω·m（7）

式中：ω*m为给定转速；ωm为实际转速；i*q为速度环控制器的输出。

设计滑模面函数为

s=cx1+x2（c>0）（8）

求导得：

s·=cx2－3pnψf2Jiq+BJω·m（9）

式中：c为滑模面参数。

2）趋近律设计

引用指数趋近律设计控制器，其控制表达式为

s·=－k1s－k2sgn（s）（k1>0，k2>0）（10）

式中：sgn（s）为符号函数；k1、k2为常数。

联立式（9）和式（10）可得：

iq=2J3pnψf∫t0[（BJ－c）ωm·+k1s+k2sgn（s）]dt（11）

3）穩定性分析

为了证明滑模控制系统的稳定性，选取李雅普诺夫函数为

V=12s2，（s≠0）（12）

联立式（11）和式（13）可得：

V·=－s[k1s+k2sgn（s）]（13）

因k1 >0、k2 >0，s×sgn（s） >0得V·<0，从而证明了控制系统的稳定性。

2.3降阶线性自抗扰控制

设计的速度环降阶线性自抗扰控制器主要由比例反馈控制模块（P）和二阶线性扩张状态观测器（LESO）组成[14-15] ，为了不引起相位滞后，省略了跟踪微分器（TD），其结构见图3。

整理式（4）和式（5）得：

dωmdt=3pnψf2Jiq－TLJ－BrωmJ（14）

设b0=3pnψf /2J为速度环控制器电流增益；f1=（-TL-Br ωm）/J为速度环控制回路内部扰动。将式（14）改写为

dωmdt=f1+b0iq（15）

1）二阶LESO设计

根据式（15）设计线性扩张状态观测器。设速度环外部扰动为f2，则总扰动为f=f1+f2，y为系统的输入，得以下系统状态方程：

y=ωmx1·=x2+b0iqx·2=f·（16）

由上式可得观测器的空间状态方程：

x1·x2·=0100x+b00iq+01f·y=10x（17）

根据线性扩张状态观测器理论，可得微分方程模型为

Z1=Z2+b0iq+β1（ωm－Z1）Z2=β2（ωm－Z1）（18）

式中：Z1为控制系统ωm的观测值；Z2为控制系统总扰动的观测值；β1、β2为线性扩张状态观测器的增益。

二阶线性扩张状态观测器稳定的前提条件是式（18）的特征方程的特征值均为负值，如下式：

s2+β1s+β2=（s+ω0）2（19）

式中：ω0为观测器带宽，且ω0>0。将β1、β2用ω0表示可得：

β1=2ω0β2=ω20（20）

2）线性误差状态反馈控制律为

iq=Kp（ωm－Z1）－Z2b0（21）

式中：Kp为自抗扰控制器速度环控制器比例因数，一般而言Kp=ωc，ωc为速度环系统带宽。

3仿真分析

为了证明所设计的复合控制器的有效性和实用性，在MATLAB/Simulink中建立仿真实验模型，分别对滑模控制器和复合控制器进行观测，电机参数设置见表1，仿真条件设置见表2。

3.1加权因子的选取

当系统反馈的速度误差信号的绝对值大于速度误差给定值的0.4时（本文中的0.4是经过多次调试后得到的），复合控制中滑模起主导作用，小于时自抗扰起主导作用，始终控制指数滑模和降阶线性自抗扰的比重和为1，经过反复的不同比重选择实验，最终确定加权因子的值为0.4时，控制系统的鲁棒性最好。

3.2加减速跟踪实验

加减速跟踪实验从0仿真到3 s结束，初始转速为500 r/min，在1 s时将转速加到1 200 r/min，然后在2 s时将转速减到500 r/min，在整个仿真过程中，负载保持不变，一直为10 N·m。

正反转跟踪实验从0仿真到3 s结束，初始转速为500 r/min，在1.5 s时将转速变到-500 r/min，在整个仿真过程中，负载保持不变，一直为10 N·m。

综合图4和图5，从仿真结果来看，采用滑模控制时，在加减速和正反转阶段都出现了较大的抖振，且超调量较大。采用复合控制后，从图4和图5可以看出，抖振明显减少，且均实现无超调跟踪，并能够更快地收敛至参考速度，显著提升了控制系统性能。

3.3負载突变仿真实验

为了验证控制策略在负载突变时的适应性，设计实验：从0仿真到3 s结束，初始负载为0，在1 s时，将负载加到10 N·m，然后在2 s时，将负载全部卸掉，仿真过程中转速为500 r/min恒定不变。

综合图6，从仿真结果来看，采用滑模控制时，在加卸载阶段都出现了不同程度的抖振和超调。采用复合控制后，从图6可以看出，复合控制相比于滑模控制，抖振明显减少，且在加载和卸载阶段超调量减少了17%和18%，提高了系统的稳定性和鲁棒性。

4结论

复合控制策略的主要优点如下：

1）通过引入指数滑模控制，利用其快速的动态响应收敛能力，提升系统的响应收敛时间。

2）通过引入降阶线性自抗扰控制，利用其较强的稳定性和抗干扰能力，提升控制系统的自抗扰能力。

3）通过不同加权因子的设置，可以实现滑模控制和线性自抗扰控制的不同权重组合，在参数适当的情况下，实现更好的控制品质和更高的控制性能。

综上所述，基于滑模和线性自抗扰的复合控制策略是一种有效的控制方法，适用于PMSM等控制系统中的速度环控制。

参考文献：

[1]张兴莲. 基于DSP+CPLD的数字化交流伺服的研究[D]. 西安： 长安大学， 2007.

[2]伏结盛. 电动汽车用双层永磁体永磁同步电机的设计与研究[D]. 赣州： 江西理工大学， 2022.

[3]路晓宇. 主动型假肢膝关节的神经网络滑模控制方法研究[D]. 天津： 河北工业大学， 2020.

[4]李佳伦， 宋桂英， 郭慧敏. 改进型自适应滑模观测器的PMSM无速度传感器[J]. 微电机， 2020， 53（1）： 47-53.

[5]孙继卫， 刘秀敏， 郭亚男. 基于扰动观测器的永磁同步电机复合滑模控制[J]. 电气传动， 2018， 48（2）： 14-18.

[6]WU Y J， CHENG Y B， WANG Y L. Research on a multi-motor coordinated control strategy based on fuzzy ring network control[J]. IEEE Access， 2020， 8： 39375-39388.

[7]刘芳璇， 娄刘娟， 虞梦月， 等. 电力机车PMSM自适应模糊滑模控制[J]. 电机与控制应用， 2018， 45（3）： 35-40.

[8]王业钧， 杨德航， 李亚楠. 基于滑模直接转矩的PMSM实验平台设计与实现[J]. 邵阳学院学报（自然科学版）， 2023， 20（4）： 32-38.

[9]刘胜， 郭晓杰， 张兰勇. 六相永磁同步电机鲁棒自适应反步滑模容错控制[J]. 电机与控制学报， 2020， 24（5）： 68-78， 88.

[10]史涔溦， 马红如， 陈卓易， 等. 永磁同步电机模糊代价函数预测转矩控制[J]. 电机与控制学报， 2022， 26（1）： 1-8.

[11]郝克鹏. 基于模型的PMSM系统故障诊断及容错控制[D]. 合肥： 合肥工业大学， 2014.

[12]李耀华， 秦辉， 苏锦仕， 等. 永磁同步电机模糊自适应变开关次数权重系数模型预测转矩控制[J]. 电机与控制学报， 2021， 25（2）： 102-112.

[13]李江坪， 王兵， 颜伟平， 等. 基于转动惯量辨识与扰动补偿的永磁同步电机滑模控制[J]. 湖南工业大学学报， 2022， 36（1）： 53-60.

[14]王宇奇. 绳牵引并联机器人支撑系统的控制方法研究及样机实验[D]. 厦门： 厦门大学， 2018.

[15]魏学良， 汤廷孝， 邓益民. 基于线性自抗扰的永磁同步电机速度控制研究[J]. 机械制造， 2021， 59（10）： 44-48.