滚珠丝杠滚道法向截面测量系统

吴 剑，欧 屹，周长光，冯虎田，钱超群

（南京理工大学 机械工程学院，江苏 南京 210000）

1 引言

滚珠丝杠副由滚珠丝杠、滚珠螺母、滚珠配套组成。高精度滚珠丝杠副作为一种高效、高精度的传动部件，广泛应用于精确传动的机床进给运动中，对机床的可靠性、刚度和承载能力有很大影响［1-3］。滚珠丝杠的滚道法向截面参数影响着滚珠丝杠副的摩擦力矩、传动刚度以及定位精度等关键性能［4-6］。滚道法向截面的检测是加工中滚道控制的重要一环，直接影响产品的关键性能。因此，国内外学者对滚珠丝杠法向截面参数检测进行了大量研究。

传统的接触式测量方法为三针法，三针法使用三根量针进行手动测量，该方法操作难度高，依赖检测人员经验，测量结果偏差大［7］。Kagiwada［8］等提出用六球法对滚珠丝杠滚道法向截面参数进行动态测量和实时分析，该方法测量精度高，但效率很低。大多数现代制造公司倾向于使用Jenoptik，Taylor Hobson，Mahr 等工业测量公司推出的接触式轮廓仪检测滚道法向截面参数。在接触测量中，轮廓通常沿滚珠丝杠滚道的滚道法向截面测量。接触式测量可以达到比较高的测量精度，但必须对测头进行调整，以测量每一个滚道。接触式测量需要经验丰富的人员进行操作且每测量一个滚道都需要调整测头，无法实现滚道的快速连续测量。基于光学测微计的滚道法向截面检测方法具有检测精度与效率高且没有测头磨损的优点，适用于滚珠丝杠滚道之类复杂滚道法向截面的检测［9-11］。冯虎田等［12］提出非接触式丝杠滚道法向截面测量方法，但是缺少完善的实验装置和全面的误差分析。

滚道法向截面数据处理算法主要分为毛刺去除，圆弧划分，圆弧拟合和参数计算4 个部分。在丝杠滚道测量过程中，由于机械振动、系统噪声与待测物体表面的粗糙度等的影响，测量得到的数据会产生毛刺点［13］。荣乾锋［14］在数据预处理阶段加入滤波算法，过滤了毛刺点。冯虎田等［12］提出了线性划分圆弧方法、最小二乘法拟合圆弧、滚珠圆心位置的计算方法以及滚道参数的计算方法。但是上述滚珠丝杠滚道法向截面数据处理算法有两个问题。一个问题是：在实际制造环境中，滚珠丝杠滚道的正常轮廓通常包括两个圆弧、两个倒角和一个储油槽。由于圆弧是与滚球接触的主要区域，在进行圆拟合前有必要选择滚道的有效圆弧。传统的圆弧划分方法是径向线性划分，在径向上用水平线将采集的轮廓分成五段，去掉倒角和储油槽后，剩下圆弧轮廓。这种划分方法依赖检测人员的经验，并且由于选择的圆弧区域难以包含圆弧绝大部分有效部分，选择不同的圆弧区域，最终计算出的参数也不一样。另外一个问题是：在丝杠滚道法向截面数据点采集过程中，传感器在丝杠轴线方向以匀速，相同频率采集螺旋滚道法向截面数据点的情况下，单位弧长上采集的点的数量在不断变化。采集的轮廓点在圆弧上非均匀分布时只运用最小二乘法会出现拟合精度不高的状况［15-16］，最终拟合的圆弧半径以及计算出的滚珠与滚道接触角精度较低。

本文建立了基于光学测微计的滚珠丝杠滚道法向截面测量系统，对原有检测算法进行优化，并对检测系统的误差进行分析。首先，根据光学测微计和直线光栅尺同步采集丝杠滚道轮廓上数据点的方式设计滚珠丝杠滚道法向截面检测装置。其次，对滚道法向截面数据处理算法进行优化：划分圆弧阶段提出角度划分圆弧划分方法，以方便操作人员选取有效圆弧，提高滚道法向截面参数的收敛性；圆弧拟合阶段提出圆弧数据均匀化方法，提高圆弧拟合的精度。接着，分析光学测微计、光栅尺的安装误差，水平移动平台直线度误差，光学测微计、光栅尺本身的误差，并进行误差补偿。最后，通过实验验证检测装置和优化后算法组成的整个检测系统的性能。

2 检测装置设计

2.1 丝杠滚道法向截面测量原理

滚珠丝杠滚道法向截面参数无法直接测量，需要测量出丝杠滚道法向轮廓上一系列点的横坐标X值和纵坐标Y值。再通过滚道法向截面数据处理算法处理采集的轮廓点，得到滚道的圆弧半径、滚珠与圆弧接触角。

滚道轮廓X，Y坐标值可以通过位移传感器测量得到。由于丝杠滚道是螺旋滚道，丝杠滚道法向轮廓纵坐标Y可以通过光学测微计旋转一个螺旋升角测量，横坐标X可以通过直线光栅尺同步测量。测量出的滚道法向轮廓曲线如图1所示。

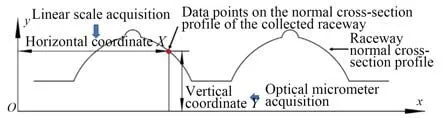
图1 滚道法向轮廓测量原理Fig.1 Measuring principle for normal profile of raceway

光学测微计的测距原理如图2 所示。绿色LED 光源发射高亮度辐射光，辐射光通过专用的散射模组以及准直仪镜头变成均匀的平行光，平行光照射到被测物体上。然后，被测物体的影像即通过远心光学系统显示在高速线性CCD 上。控制器中的数字边缘检测处理器和CPU 处理高速线性CCD 的输出入射信号，获得被测物体的尺寸。

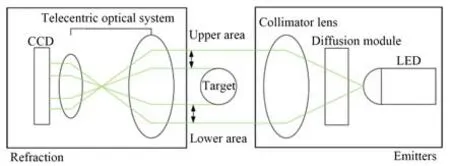
图2 光学测微计测量原理Fig.2 Measuring principle of optical micrometer

当一个目标物位于图2 所示的测量区域时，进入接收器的光线会被部分遮断，形成上边测量区域和下边测量区域，选择不同区域可以测量目标物上边或者下边的边缘与光幕上边缘或者下边缘的距离。选择下边测量区域，若传感器旋转一个螺旋升角，即可测量出光幕下边缘与滚道轮廓下边缘的距离。

2.2 滚珠丝杠滚道法向截面检测装置

检测装置的总精度通常为被测值的1/3～1/10，本检测装置取1/3，即检测装置的测量总精度为丝杠公差的1/3。由滚动功能部件产品标准汇编查得精度等级为1，2 级的滚珠丝杠螺纹滚道的法向截形误差允差值为±15 μm，由此可知，本系统滚道面形误差测量仪的总体精度要求在±5 μm 内。考虑检测装置的经济性，选用基恩士的LS-7070 光学测微计，其精度为±3 μm。选用海德汉的LIDA487 直线光栅尺，其精度为±3 μm。

根据提出的丝杠滚道法向截面测量原理，设计的检测装置如图3 所示，建立的检测装置坐标系遵循右手螺旋法则。测量前，将2 个V 型块架在床身的V 型滚道上，固定待测丝杠。伺服电机旋转，通过传动滚珠丝杠副将旋转运动变为直线运动带动水平移动平台沿X0方向移动。调节转台角度使光学测微计绕Y0轴旋转丝杠导程角，使光幕面与丝杠滚道法向截面垂直，如图4 所示。

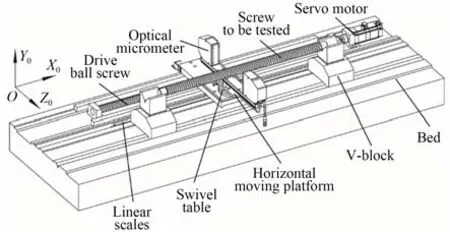
图3 滚珠丝杠滚道法向截面测量装置机械结构Fig.3 Mechanical structure of ball screw raceway normal section measuring devices

图4 滚珠丝杠滚道法向截面测量装置检测实物Fig.4 Physical drawing of ball screw raceway normal section measuring devices

丝杠滚道法向截面检测系统如图5 所示。滚道法向截面检测软件通过运动控制器控制电机旋转，电机通过传动滚珠丝杠副将旋转运动变为直线运动，带动水平移动平台沿X0方向移动。光学测微计和光栅尺测量头随着水平移动平台沿着丝杠滚道方向运动，移动过程中光学测微计和光栅尺同步采集数据，丝杠滚道法向截面的纵坐标值Y由光学测微计采集，丝杠滚道法向截面的横坐标值X由光栅尺采集。通过滚道法向截面数据处理算法分析采集的轮廓数据点，得到滚珠丝杠滚道的滚道法向截面参数。

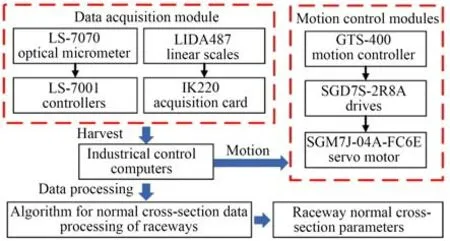
图5 滚珠丝杠滚道法向截面测量系统原理Fig.5 Schematic diagram of ball screw raceway normal section measurement system

3 滚道法向截面数据处理优化算法

滚珠丝杠的滚道法向截面参数为左右圆弧半径，滚珠与左右圆弧接触角。考虑到滚道法向截面参数无法直接得到，对原始轮廓点进行数据处理。在滚道法向截面数据处理上，传统的线性划分方法依赖检测人员经验，重复性较差；采集的离散点在圆弧上非均匀分布，直接通过最小二乘法拟合圆弧会出现拟合精度不高的情况。针对上述问题，本文对原有数据处理进行优化，提出角度划分圆弧方法替代线性划分圆弧方法，降低圆弧划分难度，计算出的圆弧参数最终收敛，并在圆弧拟合阶段之前加入圆弧数据均匀化处理，提高圆弧拟合精度。

3.1 角度划分圆弧

角度划分圆弧示意图如图6 所示。先初步拟合出圆弧圆心和半径，以拟合滚道圆弧圆心为圆心，以γ为角度，以圆弧圆心和滚道的接触点连线为中线，向中线两边画划分线，以两个划分线中间的数据点作为最终拟合的圆弧数据点，分离出的圆弧数据点，相对于滚珠与滚道圆弧接触点对称。不断增大γ，选取的圆弧最终包含绝大部分有效圆弧。此时计算出的滚道法向截面参数波动较小，收敛，降低了操作难度。详细流程如下：

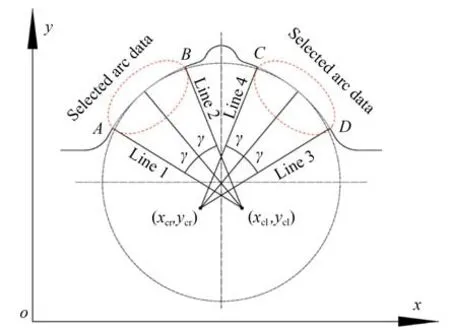
图6 角度划分圆弧示意图Fig.6 Schematic diagram of angle division arc

（1）先拟合出滚道左右圆弧圆心和半径，第一次拟合出的左圆弧的圆心为（xcl，ycl），左圆弧半径为rl，左圆弧接触角为αl。右圆弧的圆心为（xcr，ycr），右圆弧半径为rr，右圆弧接触角为αr。以拟合滚道圆弧圆心为圆心，以γ为角度，以圆弧圆心和滚道的接触点连线为中线，向中线两边画划分线，得到划分线一、二、三、四。

（2）划分线一、划分线二与左圆弧交于点A，B。划分线三、划分线四与左圆弧交于点D，C。A点坐标为（xlf，ylf），B点坐标为（xle，yle），C点坐标为（xre，yre），D点坐标为（xrf，yrf）。则分离后左圆弧的圆心和A点连线与过圆心的中垂线的角度θlf，圆弧的圆心和B点的连线与过圆心的中垂线的角度θle为：

（3）分离后右圆弧的圆心和C点连线与过圆心的中垂线的角度θrf，圆弧的圆心和D点的连线与过圆心的中垂线的角度θre为：

（4）根据坐标系中圆心、半径、角度和圆上点坐标的关系，A，B，C，D的坐标如下：

（5）左圆弧数据点的横坐标在xlf和xle之间，右圆弧数据点的横坐标在xre和xrf之间。通过循环，取出xlf和xle之间的轮廓点为划分出的左圆弧轮廓点，取出xre和xrf之间的轮廓点为划分出的右圆弧轮廓点。

（6）给定划分角度的起始值、终止值和间隔值，通过循环计算出每一个划分角度。划分角度由初始值不断增加，提取的圆弧最终会包含绝大部分有效圆弧。根据不同的划分角度提取出不同的圆弧，并通过数据处理算法计算出滚道法向截面参数。当滚道法向截面参数趋于平稳时，以划分角度γ提取的圆弧包含绝大部分有效圆弧。

3.2 圆弧数据均匀化

本文采取最小二乘法曲线拟合法拟合圆弧轮廓点。由于采集的离散点在圆弧上非均匀分布，直接用最小二乘法拟合圆弧的精度不高。针对这种情况，本文对原始圆弧数据点进行均匀化处理，在角度划分圆弧的基础上，先用原始轮廓点拟合出滚道左右圆弧的圆心和半径，再以拟合的圆弧圆心为圆心，每隔一定角度θ，在划分出的圆弧原始轮廓点内选取点。此时选取的点在单位弧长上是均匀分布的，用最终选取的点通过最小二乘法进行圆弧拟合。圆弧数据均匀化如图7所示。

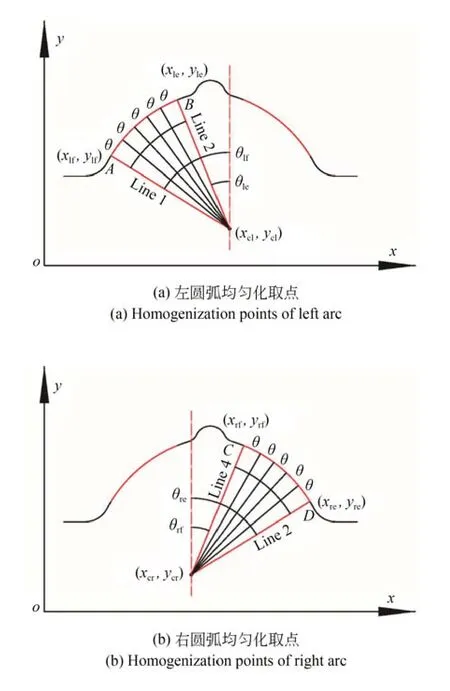
图7 圆弧均匀化示意图Fig.7 Schematic diagram of arc homogenization

根据角度划分圆弧算法，分离出左右圆弧。以θlf为初始角度，θle为最终角度，以θ为间隔做划分线，如图7（a）所示。以θrf为初始角度，θre为最终角度，以θ为间隔划分做划分线，如图7（b）所示。根据式（4）通过循序分别计算左右圆弧划分线与中垂线的锐角度θl（i）和θr（j）。当θl（i）＞θle时，左圆弧停止循环；θr（j）＞θre时，右圆弧停止循环，即：

完成间隔线划分后，根据坐标系中圆心、半径、角度和圆上点坐标的关系公式，通过循环求出左圆弧划分点（x2l（i），y2l（i）），右圆弧划分点（x2r（i），y2r（i）），计算公式如下：

圆弧离散点上距离划分点最近的点为间隔点。通过循环计算滚道轮廓上每一个离散点与每一个划分点的距离，再通过循环判断距离一系类划分点距离最近的点，这些点为间隔点。间隔点在单位圆弧上是均匀分布的。

给定间隔角度的起始值、终止值和间隔值，通过循环计算出每一个间隔角度。间隔角度由初始值不断减小。用不同的间隔角度提取圆弧数据点，并通过数据处理算法计算出滚道法向截面参数。当滚道法向截面参数趋于平稳时，将θ认定为最终的间隔角度。

4 误差分析

根据测量数据来源，滚珠丝杠滚道法向截面检测装置的主要误差来源有：光学测微计、光栅尺的安装误差，水平移动平台直线度误差，以及光学测微计、光栅尺本身的误差。

4.1 传感器安装误差

传感器的安装误差分为光学测微计安装误差和光栅尺安装误差。建立床身、待测工件与传感器系统坐标系，其中，床身、待测工件坐标系为空间笛卡尔坐标系，传感器系统由于安装误差为斜坐标系。检测系统坐标系定义与传感器安装误差如图8 所示。

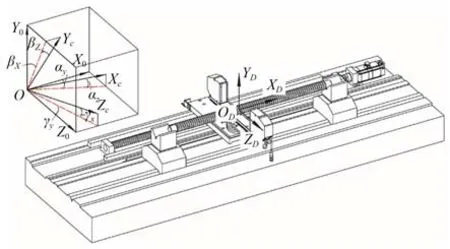
图8 检测系统坐标系定义与传感器安装误差Fig.8 Definition of detection system coordinate system and sensor installation error

工件的空间直角坐标系为OD-XDYDZD，其中XD轴沿丝杠长度方向；YD轴在竖直平面内与XD轴垂直，且方向向上；ZD轴在水平面内与平面ODXDYD垂直。床身的空间直角坐标系为OX0Y0Z0，其中X0轴沿床身的长度方向；Y0轴沿着床身竖直方向，与X0垂直；Z0轴沿着床身宽度方向，在水平面内与平面O-X0Y0垂直。位移传感器系统的斜坐标系为O-XCYCZC，其中XC轴沿着光栅尺测量的方向，YC轴为沿着光学测微计测量的方向，ZC轴沿光学测微计的激光发射方向。本文在研究传感器安装误差时，不考虑待测丝杠坐标系与床身坐标系之间的偏转，假设丝杠坐标系与床身坐标系重合。

光栅尺安装过程中，光栅尺的XC轴线方向与床身坐标系X0轴线方向并非完全一致，光栅尺XC轴线与X0轴线在水平面O-X0Z0上的误差为αy，光栅尺XC轴线与X0轴线在竖直平面O-X0Y0上的误差为αz。光学测微计安装过程中，其测量轴YC与Y0在竖直平面O-Y0Z0上的误差为βx，测量轴YC与Y0在竖直平面O-X0Y0上的误差为βz。激光发射轴ZC与Z0在竖直平面O-Y0Z0上的误差为γx，激光发射轴ZC与Z0在水平面O-X0Z0上的误差为γy。

根据光学测微计的工作原理，βx和γx对测量轴类和球类零件没有影响。在考虑βz，γy，αy和αz其中一个误差对测量的影响时，其他误差为0。滚珠丝杠滚道法向截面检测时光栅尺沿床身X0轴的测量值为Δx，光学测微计在Y0上的测量值为Δy。

（1）若只存在光学测微计在竖直平面内的安装误差βz，将直角坐标系O-X0Y0中的点（x0，y0）转化到斜坐标系O-XCYC的点（xcβz，ycβz）上，转化公式为：

则实际测量得到的丝杠滚道法向截面滚道的误差为：

式中：δxβz为X0轴方向误差，δyβz为Y0轴方向误差。

（2）若只存在光学测微计在水平面内的安装误差γy，将直角坐标系O-X0Y0中的点（x0，y0）转化到斜坐标系O-XCYC的点（xcγy，ycγy）上，转化公式为：

则实际测量得到的丝杠滚道法向截面滚道的误差为：

式中δxγy为Y0轴方向误差。X0轴方向误差为0。

（3）若只存在光栅尺在水平面内的安装误差αy，将直角坐标系O-X0Y0中的点（x0，y0）转化到斜坐标系O-XCYC的点（xcαy，ycαy）上，转化公式为：

则实际测量得到的丝杠滚道法向截面滚道的误差为：

式中：δxαy为X0轴方向误差，δyαy为Y0轴方向误差。

（4）若只存在光栅尺在竖直面内的安装误差αz，将直角坐标系O-X0Y0中的点（x0，y0）转化到斜坐标系O-XCYC的点（xcαz，ycαz）上，转化公式为：

则实际测量得到的丝杠滚道法向截面滚道的误差为：

式中δxαz为Y0轴方向误差。X0轴方向误差为0。

滚珠丝杠滚道法向截面检测时，单个滚道光栅尺沿床身X0轴测量值Δx一般小于10 mm，光学测微计在Y0上的测量值Δy一般小于5 mm。将安装误差βz控制在0.01°之内，则δxβz小于0.87 μm，δyβz小于0.0007 6 μm；将安装误差γy控制在0.01°之内，则式中δxγy小于0.000 15 μm；将安装误差αy控制在0.01°之内，则δxαy小于0.000 15 μm，δyαy小于1.74 μm；将安装误差αz控制在0.01°之内，则δxαz小于0.000 15 μm。此时可忽略光学测微计和光栅尺的安装误差。为了尽可能减小传感器的安装误差，对安装基准面进行高精度研磨，提高安装面精度。

光栅尺XC轴线与X0轴线在水平面O-X0Z0上的误差αy：安装直线光栅尺时，以导轨上平面为基准面，用千分表测量直线光栅尺的上平面相对于基准面的平行度，实验安装要求是每一米平行度在4 丝之内。安装人员通过研磨床身的上安装基准面，并调节光栅尺的安装位置，最终一米内的平行度为35 μm，千分表数值最小处距离测量起始点约261 mm，千分表数值最大处距离测量起始点约654 mm，此时误差αz≈0.005 1°。光栅尺XC轴线与X0轴线在竖直平面O-X0Y0上的误差αz：安装直线光栅尺时，以导轨为侧平面为基准面，用千分表测量直线光栅尺的侧平面相对于基准面的平行度，实验要求是每一米平行度在4 丝之内。安装人员通过研磨床身的侧安装基准面，并调节光栅尺安装位置，最终一米内的平行度为37 μm，千分表数值最小处距离测量起始点约375 mm，千分表数值最大处距离测量起始点约826 mm，此时误差αz≈0.004 7°。光学测微计的测量轴YC与Y0在竖直平面O-X0Y0上的误差βz：安装光学测微计之后，在光学测微计上表面沿X0方向放置电子角度仪。通过研磨光学测微计的安装板，调节误差βz的大小。调节后误差βz为0.009°光学测微计激光发射轴ZC与Z0在水平面O-X0Z0上的误差为γy：安装光学测微计时，以导轨测平面为基准面，用千分表测量光学测微计的侧平面。通过调节光学测微计与安装板之间的位置，调节误差γy的大小。光学测微计的侧平面长度为454 mm，千分表数值大约处在光学测微计的侧平面起始处，千分表数值最小处约在光学测微计的侧平面终止处，此时误差γy≈0.002 5°。传感器的安装误差可以忽略。

4.2 水平移动平台直线度误差

水平移动平台的直线度误差分为竖直直线度误差和水平直线度误差。根据光学测微计的测量原理，水平直线度误差不会给测量结果带来影响。竖直直线度误差叠加到竖直方向的测量值上，会影响测量结果。水平移动平台的垂直直线度误差使用Renishaw 激光干涉仪系统XL-80进行测量，测量实物如图9 所示。

图9 直线度测量装置Fig.9 Straightness measurement setup

垂直直线度误差的测量方法是：首先调整激光与床身的表面平行，再将测量直线度误差的反射镜置于水平移动平台上，干涉镜置于床身上，检测软件控制水平移动平台匀速移动，利用XL-80 的定时测量功能每4 mm 采集一个数据，垂直直线度误差的实验测量长度为550 mm，共做5 次实验。

气浮平台垂直直线度测量误差两次实验中，整个长度的累计直线度误差分别为4.3，4.6，4.7，4.4，4.3 μm，每10 mm 的最大直线度误差分别为0.75，0.89，0.91，0.77，0.76 μm。在实验过程中，避开直线度误差最大的床身段测量，忽略由水平移动平台引起的直线度误差。

4.3 传感器误差

LS-7070 光学测微计的测量范围为0.5～65 mm，最高测量精度为±3 μm。传感器测量精度在一定范围内变化，通过多次测量取平均值，消除其对测量的影响。

测量环境温度直接影响光学元件测量的精度，环境温度的变化会导致测量结果发生波动。在20 ℃时，漂移为0，所以丝杠滚道法向截面检测实验在20 ℃恒温室中进行，以避免环境温度对测量结果的影响。本文选用的光栅尺为海德汉LIDA487 光栅尺，根据海德汉提供的光栅尺位置误差，对实际测量横坐标进行数据补偿，可减小光栅尺测量误差对测量精度的影响。

5 测量实验与结果

滚道法向截面检测装置误差补偿后，通过实验验证检测装置和优化后算法组成的整个检测系统，从算法优化后滚道法向截面参数的收敛性，整个检测系统的精度、重复性三个方面进行验证。

5.1 收敛性

滚珠丝杠滚道法向截面检测装置采集1 个滚道轮廓的数据点，分别用优化前后的数据处理算法计算。优化前采用线性划分圆弧，选择9 个划分区域，如图10 所示。

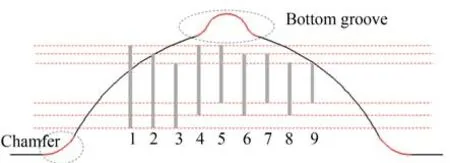
图10 线性划分区域Fig.10 Linear division of areas

优化后采用角度划分圆弧，从1°开始选择不同的划分角度γ，每次增加1°，若最终拟合的滚道参数趋于平缓，停止增加角度。滚道法向截面数据处理算法优化前后计算出的圆弧参数如图11 所示。可以发现算法优化前，线性划分圆弧选择的九段圆弧的拟合结果是不规则的，主要是因为划分的圆弧不包含所有有效圆弧数据，圆弧的拟合结果较为离散；而算法优化后，角度划分圆弧所选择的数据点，由于相对于滚珠与圆弧的接触点更加对称，随着γ的增加，选取的圆弧最终包含所有有效圆弧数据，可以看出，最终计算出的滚道圆弧参数波动变小，参数更加收敛。

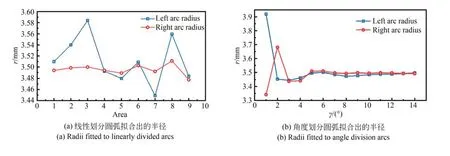
图11 线性和角度划分圆弧方法计算出的参数对比Fig.11 Comparison of parameters computed by linear and angular arc division methods

5.2 精度、重复性和不确定度

为了验证本文算法的精度、重复性和不确定度，将优化算法计算的数据与现有两种检测方法计算的数据进行对比。第一种方法是传统的接触式测量，第二种是未优化前的算法。传统的接触式测量系统的测量数据由厂家提供，并作为标准值。厂家的检测装置为Opoacom 公司生产的型号为VC-10-series 的接触式轮廓仪，其测量精度为±0.5 μm。

多次测量同一段滚道，对比算法优化前后测得的圆弧半径、滚珠与圆弧接触角的平均值与厂家提供的数据，验证整个检测系统的精度；对比测得的圆弧半径、滚珠与圆弧接触角的标准偏差，验证整个检测系统的重复性；对比测得的圆弧半径、滚珠与圆弧接触角的不确定度，验证整个检测系统的可信赖度。

检测装置误差补偿后，滚道法向截面检测装置测量待测丝杠同一个截面的3 个滚道5 次，分别用优化前后算法计算出滚道法向截面参数，计算5 次测量值的平均值为最终结果。算法优化前后和厂家提供滚道法向截面参数如表1 所示。计算算法优化前后滚道法向截面参数与厂家提供数据的误差如表2 所示。计算5 次测量值的标准偏差如表3 所示，计算5 次测量值的A 类不确定度如表4 所示。表中，rL为左圆弧半径，rR为右圆弧半径，αL为滚珠与左圆弧接触角，αR为滚珠与右圆弧接触角。

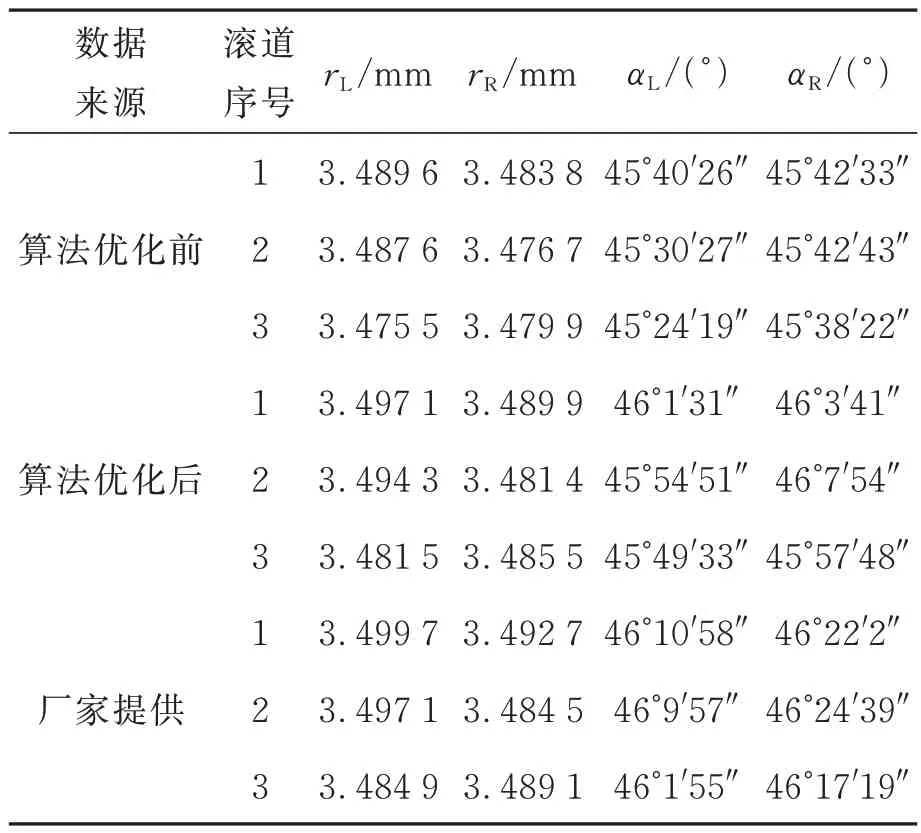
表1 算法优化前后滚道法向截面参数和厂家提供数据Tab.1 Normal sectional parameters calculated by algorithm before and after optimization and value provided by manufacturer

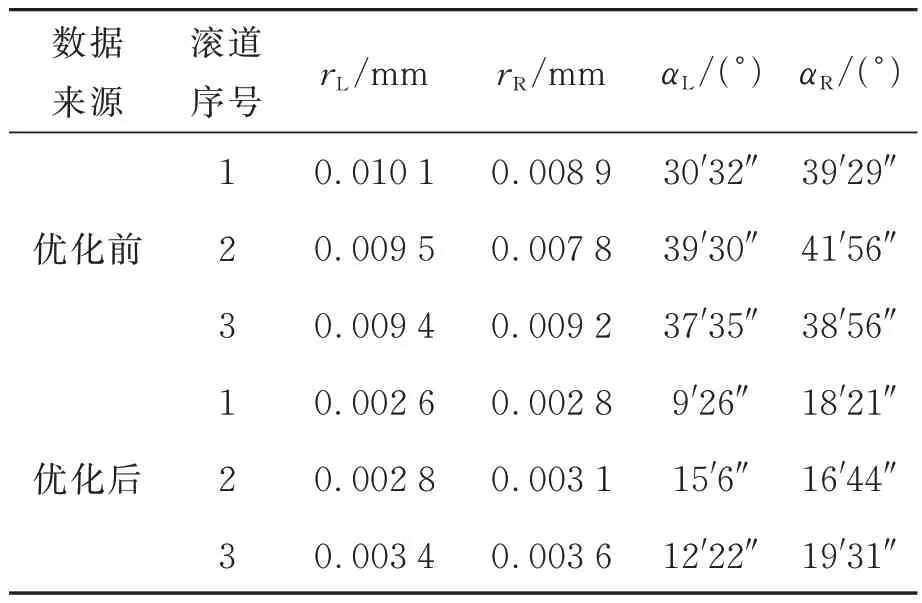
表2 算法优化前后滚道法向截面参数与厂家提供数据的误差Tab.2 Error between parameters of optimized surface and values provided by manufacture

表3 滚道法向截面数据处理算法优化前后滚道法向截面参数的标准偏差Tab.3 Standard deviation of surface parameters before and after optimization of surface data processing algorithm

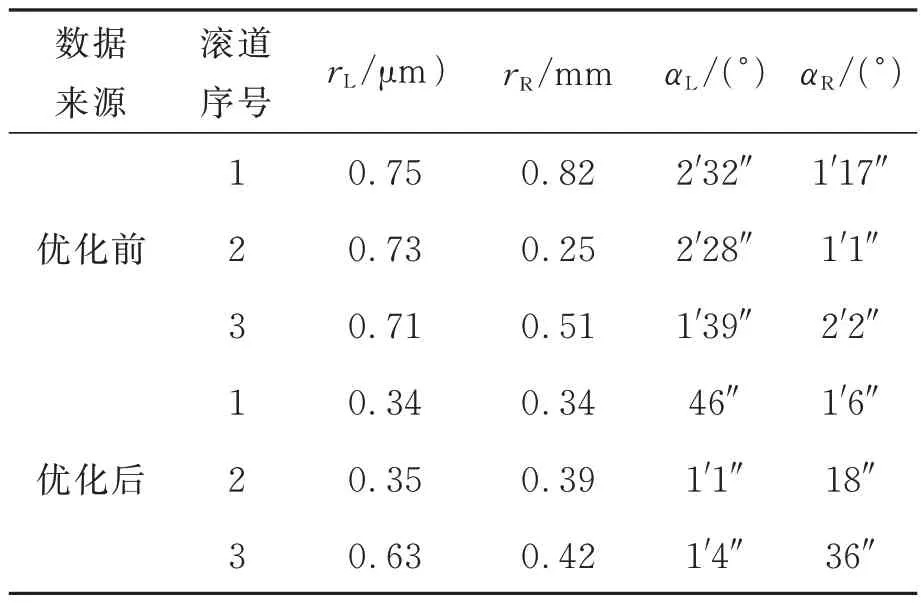
表4 滚道法向截面数据处理算法优化前后滚道法向截面参数的A 类不确定度Tab.4 Class A uncertainty of surface parameters before and after optimization of surface data processing algorithm

由表2 可以发现，算法优化前滚道法向截面检测系统测得的圆弧半径和滚珠与圆弧接触角与厂家提供数据的误差最大值分别为10.1 μm和41′56″。算法优化后滚道法向截面检测系统测得的圆弧半径和接触角与厂家提供数据的误差最大值分别为3.6 μm 和19′31″，算法优化后的误差较低，相对于算法优化前的误差分别降低64.36%和53.46%。算法优化后的滚道法向截面检测系统精度满足要求。

由表3 可以发现，算法优化前滚道法向截面检测系统测得的圆弧半径和滚珠与圆弧接触角的标准偏差最大值分别为2.02 μm 和6′12″。算法优化后滚道法向截面检测系统测得的与厂家提供的圆弧半径和接触角的标准偏差最大值分别为1.56 μm 和2′41″，算法优化后标准偏差较低，相对于算法优化前的误差分别降低22.77%和56.67%。算法优化后的滚道法向截面检测系统重复性满足要求。

在检测工作中，检定结果的不确定度评定是重要内容之一。本文采用不确定度A 类评定方法来评定。由表4 可知，算法优化前滚道法向截面检测系统测得的圆弧半径和滚珠与圆弧接触角的A 类不确定度最大值分别为0.82 μm 和2′32″。算法优化后滚道法向截面检测系统测得的圆弧半径和滚珠与圆弧接触角的A 类不确定度最大值分别为0.63 μm 和1′6″，相较算法优化前圆弧半径和滚珠与圆弧接触角最大分别降低56%和70%。算法优化前后，检测结果的A 类不确定度都较低，优化后的A 类不确定度更低。

6 结论

本文建立基于光学测微计的滚珠丝杠滚道法向截面测量系统，优化原有滚道法向截面数据处理算法，对检测系统的误差进行分析和补偿。通过实验验证了算法优化后检测系统的精度和重复性。实验结果表明，法向截面圆弧半径和接触角算法优化后精度分别提升了64.36% 和53.46%，重复性分别提升了 22.77% 和56.67%，不确定度分别降低了56%和70%。

本文通过对检测系统、数据处理算法以及检测误差的研究，实现了滚珠丝杠滚道法向截面的无损检测，并提高了检测精度、重复性和不确定度，为轴承、阳转子、蜗杆等其他零件的滚道截面的无损检测提供了技术支持。