基于投影光瞳分布的星地激光通信波前探测

杨慧哲，张贞钰，刘 进，梁永辉

（1.国防科技大学 前沿交叉学科学院，湖南 长沙 410073；2.国防科技大学 南湖之光实验室，湖南 长沙 410073；3.河北汉光重工有限责任公司，河北 邯郸 056017）

1 引言

在星地激光通信系统中，光束经过大气湍流产生波前畸变，激光束发生弥散，导致到靶功率大幅下降。通常需要采用自适应光学（Adaptive Optics，AO）系统对波前畸变进行实时补偿，以恢复信号光，降低误码率。星地激光通信包括星对地下行激光链路和地对星上行激光链路，对两路光信号的校正一般由地面端AO 系统完成，具体是通过测量星对地的下行激光的波前畸变，然后将该畸变施加给变形镜（Deformable Mirror，DM），从而实现对下行激光的AO 校正和对上行光路的预校正。例如，美国航空航天局（NASA）建造的用于激光通信的1 m 望远镜地面站［1-2］，其自适应光学闭环校正后的斯特列尔比从低于0.02 提高到0.6。德国航空航天中心DLR 和欧洲航天局领导 的Alphasat 项目［3-4］使用1 m 口 径的地面站，在强湍流r0≤5 cm（@1 064 nm）的条件下，实现了与近地轨道和同步轨道卫星的相干激光通信。2019 年，荷兰应用科学研究机构TNO 和DLR 针对高通量星地激光通信链路设计了一个光反馈链路的自适应光学预校正平台FEEDELIO。实验结果显示，通过预校正可将上行光束的平均功率提高2.5 倍，并使闪烁指数下降为原来的1/4，说明AO 系统具有良好的上行链路补偿能力［5］。刘超等［6-8］利用云南丽江的1.8 m 望远镜，在1 550 nm 通信波段对41 颗不同高度角的恒星进行了实验，证明AO 系统可以有效地消除中弱大气湍流的影响。

然而，由于通信卫星的快速运动，下行激光和上行激光所经历的大气路径是不同的，其夹角称为提前角（Point Ahead Angle，PAA）［9］。提前角过大（即卫星运动过快或湍流太强）时，下行激光测量到的波前畸变与上行激光所经过的大气湍流引起的波前畸变会完全不同，此时自适应光学系统对上行激光的预校正完全无效。Martine等［10-11］通过仿真证实以安装在泰德天文台的光学地面站OGS 大气条件为例，对于提前角只有4″的地球静止轨道（Geostationary orbit，GEO）卫星，提前角小于AO 等晕范围，因此通过下行链路对上行激光的预校正是有效的；而对于400 km的近地轨道（Low Earth Orbit，LEO），提前角远远大于AO 等晕角，通过下行链路对上行激光的预校正存在较大误差。Fraunhofer 应用光学与精密工程研究所［12-14］在2016～2019 年间进行了最大水平传播距离为1 km 的3 次自由空间激光传播实验。实验结果表明，当提前角大于水平大气等晕角（约为30″）时，自适应光学预校正对卫星站点接收的激光功率没有明显改善。

目前，还没有简单有效的方法来解决星地激光通信中自适应光学系统的提前角问题。本文采用一种新型波前探测技术——投影光瞳面分布（Projected Pupil Plane Pattern，PPPP）［15］，利用上行激光在两个不同高度的瑞利后向散射光斑来测量大气湍流。而传统的夏克-哈特曼波前探测器一般是利用星对地的下行通信激光作为导星信号。因此，PPPP 通过采用上行激光进行波前探测，避免了由于卫星飞行过快而引起的上行激光与下行激光通过大气路径不一致（即提前角）的非等晕问题。当然，由于提前角的存在，上行激光与下行激光所需的DM 校正命令是不同的，因此需要采用两套AO 系统分别对两路光进行校正。最后，通过实验手段验证了PPPP 方法用于地对星上行激光波前探测的可行性。

2 工作原理

PPPP 根据强度传输方程（Transport-of-Intensity Equation，TIE）［16］，通过不同传输距离下光强分布的演变来反解波前畸变信息。TIE 公式如下：

其中：I和φ分别表示光强分布和大气湍流相位，波数k=2π/λ，∇=∂x+∂y，h为传输距离。对于缓慢变化的光强分布I，式（1）可近似为［17］：

其中：I0，I1和I2分别对应传输距离h=0，h1和h2处的光强分布，∇2=+。根据式（2），通过测量不同传输距离下对应的光强分布I0，I1和I2，就可以反解出湍流相位φ。

图1 为基于PPPP 的星地激光通信中的自适应光学系统示意图。其中，望远镜既是上行激光（地面端到卫星）发射望远镜，也是下行激光（卫星到地面端）的接收望远镜。由于提前角的存在，上行激光和下行激光采用的AO 系统不同，图1 仅给出本文主要研究的地对星上行激光的AO 预校正系统，而使用常规方式对下行激光进行校正的AO 系统则未给出。上行激光通过地基望远镜进行扩束并发射到卫星。当上行激光到达高度h1时，使用与h1共轭的相机对上行激光在h1处的瑞利后向散射光斑进行成像，记为I1。这里h1指的是中心高度为h1的一个空气层，用Δh1来表示该空气层的厚度。在实际应用中，需要通过控制相机快门来对这个范围内的后向散射光斑进行成像。以高度10 km 的后向散射光成像为例，假设Δh1=1 km，一束脉冲激光从望远镜发射到达高度h1-Δh1/2，其后向散射光回到望远镜时经过的时间为t1=2×(h1-Δh1/2)/c=6.33×10-5s，此时相机开始曝光。当脉冲激光束继续经过厚度Δh1的大气并返回时，对应的时间为t2=2×(h1+Δh1/2)/c=7×10-5s，此时结束曝光。在曝光范围内得到的图像，即对应I1。同理，对高度h2处的后向散射光斑进行成像可以得到I2。通常采用一个快反镜对相机位置进行快速切换，从而实现单相机对h1和h2处光斑分别成像的目的。得到I1和I2后，继而利用测量到的强度差I2-I1反解出湍流相位φ。

图1 基于PPPP 的星地激光通信自适应光学系统Fig.1 Schematic diagram of satellite-ground laser communication AO system based on PPPP

本文采用一种Zernike 模式重建方法来反解大气相位［18］。首先，构建一个交互矩阵Mij：

其中：Zi为第i阶Zernike 模式，R为激光束的半径。然后，将这个方阵求逆得到控制矩阵M-1，则重构相位可表示为：

式中：a为重构相位φ的Zernike 系数，F为实测光强与Zernike 多项式的标量积，即：

需要注意的是，PPPP 方法测量的是h1高度以下整个大气传输路径上的湍流，对于高于h1的大气湍流，PPPP 方法无法进行有效测量。不过在实际中强湍流主要分布在低层，且加入AO 闭环校正后h2处信号可提供h1～h2一部分中间层的湍流信息，一定程度上可以降低中间层湍流导致的测量误差。

考虑到瑞利散射对大气分子浓度的要求，散射高度一般要在25 km 以下，又由于PPPP 主要测量h1以下高度的湍流信息，因此在实验中令h1=10 km，h2=17 km。采用以上参数，对于400 km 的LEO 卫星，上行激光从发射到由卫星接收需要400 km/c=1.33 ms，而由传输距离较远的h2=17 km 的大气返回的后向散射光所需时间为2×17 km/c=0.11 ms。在这个时间差内可以通过光强差I2-I1来反解大气湍流信号，有望降低自适应光学系统的时间误差。

3 实 验

根据PPPP 波前探测原理，实验主要包含上行激光在大气中的传输，对不同高度的瑞利后向散射光斑成像，以及基于Zernike 模式法的波前重建3 部分。根据目前主流的星地激光通信实验系统，本实验模拟望远镜口径为1 m，上行激光传输距离分别为10 km 和17 km。

PPPP 实验光路原理如图2 所示，f1，f2和f3，f4为两组中继透镜组，用以改变光束尺寸。激光束经过透镜f1，f2后入射到反射镜M0上，再经过f3，f4扩束为直径D2=10.5 mm 的准直光束。实验采用两种波前畸变模拟器件（图2 中turbulence），一种为空间光调制器（Spatial Light Modulator，SLM），另一种是简易的塑料透明片。波前畸变模拟器件放置在与M0共轭的位置。光束经过波前畸变模拟器件后，通过两个平面镜（M3和M4）到达散射屏。散射屏采用高反射度的胶带，将它放置在一个可以快速旋转的小风扇上，来模拟大气分子的高速运动。这样保证了散射光是无序的非相干光，且散射光还不是非常弱，从而可以在暗室里通过PPPP 相机（图2 红框）对散射光斑本身进行成像。

图2 PPPP 实验的光路原理Fig.2 Optical layout of PPPP experiment

为了实现对两个不同高度的后向散射光斑成像，将两个平面镜（M3和M4）固定在一个滑轨上，通过移动M3和M4来改变光束的传输距离。对不同高度的散射光斑成像是通过图2 中的PPPP 模块实现的。具体来说，散射光通过M3和M4返回，经由分束镜BS1 反射到PPPP 模块，其中f5，f6作为中继透镜组用以减小光束尺寸，f7用于对散射光的成像。

图3 给出了对后向散射光斑成像的Zemax 光路设计（虚线框为f5，f6，f7的放大图）。随着M3和M4的移动，散射光斑成像的物距也相应发生变化。实验通过调整f6，f7之间的距离（保持f7和后面相机的间距不变），保证对不同物距的光斑始终成大小一致的像。f7与相机放置在滑轨上，通过在滑轨上移动f7与相机（其间距不变），保证相机始终对散射屏上的散射光成清晰的像，并且图像尺寸保持不变。实验中两个传输距离分别为1 100 mm 和1 875 mm（相当于实际系统10 km 和17 km 的传输距离），对应的f6，f7之间的距离d分别等于100 mm 和15 mm。图4 给出了两个传输距离下系统成像的点列图。从图中可以看出，图像尺寸基本不变，约为5.25 mm，对应的波像差如图5 所示。两种结构在视场边缘的最大波前误差的均方根（Root Mean Square，RMS）分别为0.047λ和0.019λ，远小于1 rad，因此对成像质量几乎没有影响。

图3 Zemax 设计的后向散射成像Fig.3 Zemax designed backscattered reimaging

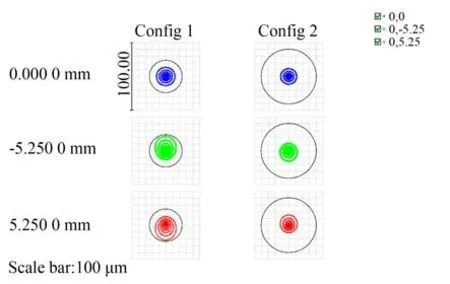
图4 两个传输距离对应的后向散射成像的点列图Fig.4 Spot diagram of backscattering reimaging with two configurations

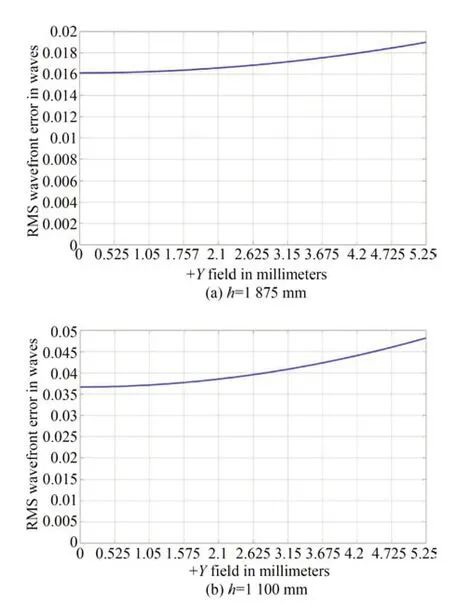
图5 h=1 100 mm 和h=1 875 mm 时不同视场的像差Fig.5 Aberrations at different field of view with h of 1 100 mm and 1 875 mm

为了与PPPP 进行对比，实验还采用通用的夏克-哈特曼波前探测器（Shack-Hartmann Wave-Front Sensor，SHWFS）来测量波前畸变（图2 中SHWFS 部分）；并使用相机记录系统的点扩散函数（Point Spread Function，PSF）（图2 中PSF 部分）。实验参数见表1。

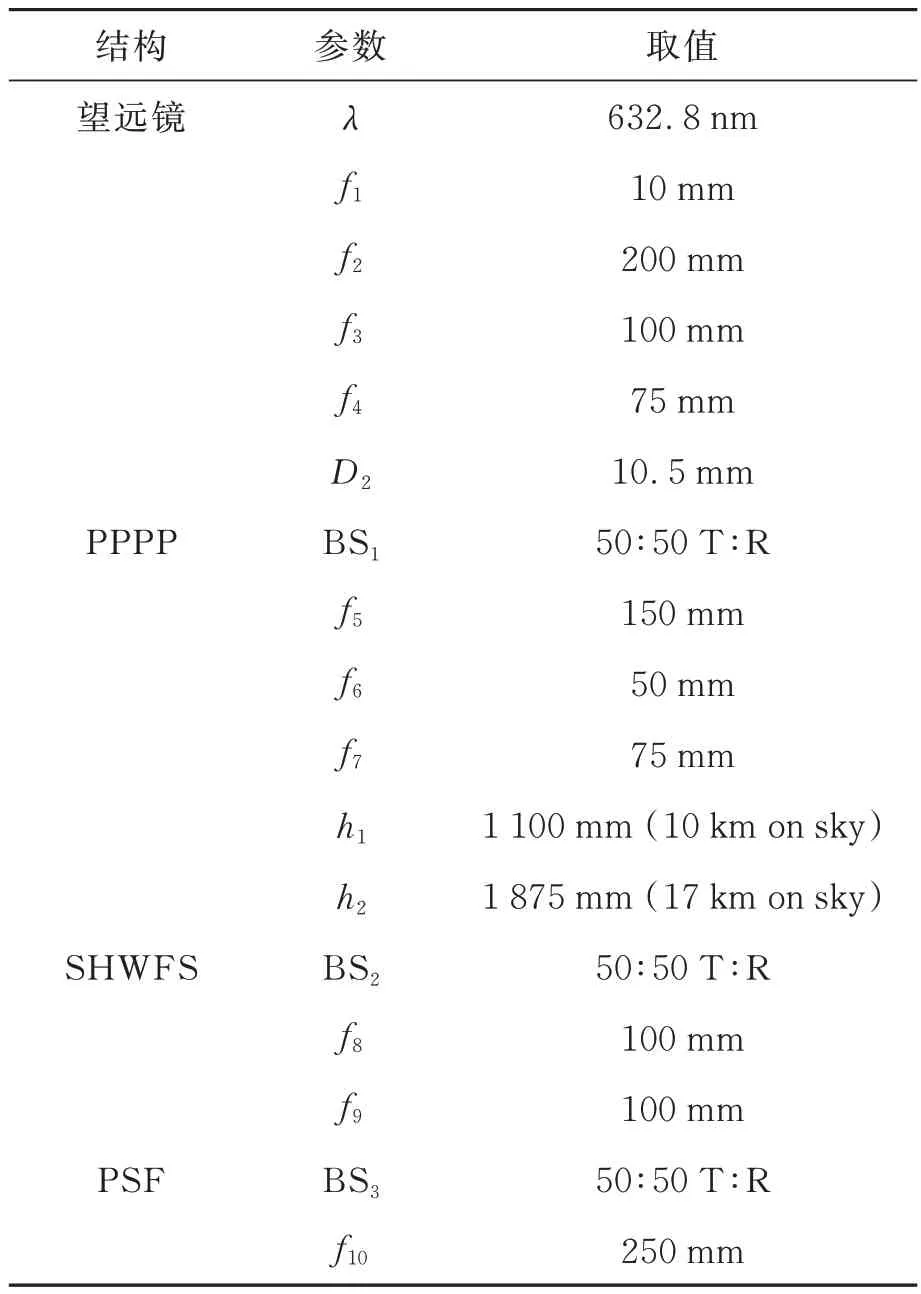
表1 PPPP 实验参数Tab.1 PPPP experiment parameters

实验中，激光器为Thorlabs 公司的HeNe 激光器（NHL020LB），中心波长为632.8 nm，功率为2 mW，光束直径为0.63 mm（按1/e2的基模宽度衡量）。相机均是IDS uEye CMOS 相机，包含3 088×2 076 个像素，像素尺寸为2.4 μm（总尺寸为7.411 mm×4.982 mm）。最短曝光时间为0.1 ms，最长曝光时间为221 ms。该相机仅支持对PPPP 波前探测技术进行实验室验证，在实际应用中，需要采用曝光时间更短、读出噪声更小、波长范围更广的科学级探测器。

波前畸变模拟器件采用透射式空间光调制器（西安中科微星光电科技有限公司，TSLM017-A），其分辨率为1 024×768，像素尺寸为36 μm，波长为380～1 200 nm。光利用率为36%@633 nm，最大相位调制为1.8π@532 nm。由于液晶填充率为70%，像素之间存在间隙，相当于在液晶表面加了一个二维光栅，使仪器出现高阶衍射光斑，因此需要在焦平面进行滤波处理。在f5，f6之间以及f8，f9之间的焦点上放置光阑，只允许中心光斑通过来阻挡高阶斑点。由于SLM 相位调制范围很小，只能施加单阶Zernike 像差来验证PPPP 波前探测方法的可行性。实验中对某一单阶Zernike 像差，正负两次加载该像差，对相应的光强进行相减从而达到放大探测信号的目的。

夏克-哈特曼波前探测器由一个35×35 子孔径的微透镜阵列和一个CMOS 相机（2 048×2 048 像素，像素尺寸为5.5 μm）组成。微透镜阵列的子孔径间距为300 μm，有效焦距为14.6 mm。夏克-哈特曼波前探测器的有效面积为11.26 mm×11.26 mm。

图6 为实验平台。PPPP 路径相较主光路的垂直方向略有倾斜，以避免来自分束器表面的反射光对后向散射光斑成像的影响。这是因为散射屏（反射胶带）的散射光强度较弱，很容易被分束器表面的反射光淹没。

图6 PPPP 实验台Fig.6 PPPP experiment bench

4 实验结果

实验中，空间光调制器位于两个位置，分别是BS1的前方（图2 中position 1）和后方（图2 中position 2），其中BS1与M0共轭。如果SLM 位于位置1，表示上行激光经过大气湍流，但后向散射光斑的成像过程中没有考虑大气湍流的影响。将SLM 放置在位置2 更符合实际，因为上行激光和后向散射光都通过了SLM。

首先，将SLM 放置于位置1 进行实验。在SLM 未加载相位时，记录传播距离h1=1 100 mm 和h2=1 875 mm 的光强信号，记为I10和I20，分别如图7（a）和7（b）所示。光瞳处的光强分布I0可近似为I10和I20的平均值（图7（c））。然后，将前15 项Zernike 模式作为简单像差逐一加载到SLM 上。为了提高相位调制的幅度，对每一个Zernike 模式正负各加载一次，其光强差即为该Zernike 模式对应的光强分布。图7（d）和7（e）给出了第6 项Zernike 模式下I1和I2的实测结果，图7（f）给出了I1和I2的差值，将其作为信号，根据式（4）进行相位重构。

图7 PPPP 实测光强分布Fig.7 Light intensity distribution measured by PPPP

根据实测数据I0建立交互矩阵M和控制矩阵M-1，如图8 所示。已知I0，I2-I1和M-1，根据式（4）就可以重构出SLM 加载的Zernike 相位，图9（a）为第6 项Zernike 像差的PPPP 重构结果，对应的SHWFS 重构结果如图9（b）所示，两者之差见 图9（c）。其中，PPPP 重构相位的均 方根为1 032.49 nm，SHWFS 为1 025.28 nm。它们的差值称作波前误差（Wavefront Error，WFE），其RMS 为305.33 nm。

图8 重构矩阵和重构逆矩阵Fig.8 Reconstruction matrix M and inverse reconstruction matrix M-1

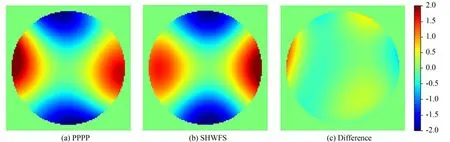
图9 PPPP 和SHWFS 的相位重构结果Fig.9 Reconstructed phases of PPPP and SHWFS

令SLM 分别加载第4～15 项Zernike 模 式后，重构结果如图10 所示。从图10 可以看出，PPPP 波前探测的精度在加入不同的Zernike 像差时有所波动，如在第4，6，7，12 等几项Zernike模式，“difference”为SHWFS 数值的四分之一，探测精度较好；但在第5，8 等几项Zernike 模式，“difference”为SHWFS 数值的二分之一，探测精度较差。

图10 第4～15 项Zernike 模式测量结果Fig.10 Reconstruction results with 4th to 15th Zernike mode

PPPP 的探测结果存在波动，且重构精度有限，其原因可能是由于过强的衍射效应引入了较大的非线性误差。为了验证这一猜想，将实验模拟的1 m 望远镜（D2=10.5 mm）改为2 m 望远镜（D2=21 mm）重新进行测量，对应的各项Zernike 相位重构结果如图11 所示。对比图10 和图11 可以看出，与1 m 望远镜相比，PPPP 和SHWFS 的波动幅度都变小，二者差值的RMS 约为200 nm，远低于1 m 口径望远镜对应的约400 nm 左右。由此可知，如果实际中采用更大口径的望远镜作为激光发射装置，可以有效降低PPPP 波前探测器的测量误差。

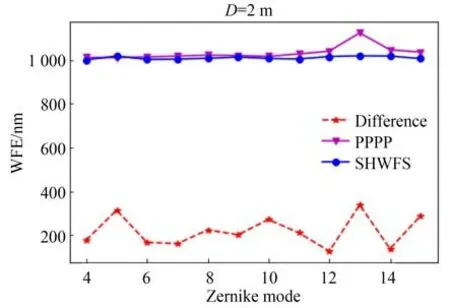
图11 望远镜直径为2 m 时第4～15 项Zernike 模式测量结果Fig.11 Reconstruction results with 4th to 15th Zernike mode for 2-m telescope

上述实验并没有考虑后向散射的能量问题，在实际中上行激光的后向散射光来源于一定厚度的大气薄层，在这个薄层范围内接收到的光子数决定了探测的信噪比。实验中可以通过改变相机的曝光时间来控制探测到的后向散射光子数，图12 给出不同光子数下PPPP 重构相位的准确度，SHWFS 给出的依然是长曝光（低噪声）下的重构结果。该实验采用第4 项Zernike 像差，图中橫坐标为PPPP 相机探测到的光子数，依次约为［1 300，2 550，6 500，12 900，25 800，45 000，90 000］。实验结果表明，随着探测光子数的增加，PPPP 和SHWFS 的重构相位之差的RMS 逐渐减小，即PPPP 和SHWFS 的重构相似度增加，PPPP 探测精度提高，这与模拟结果是一致的［19］。

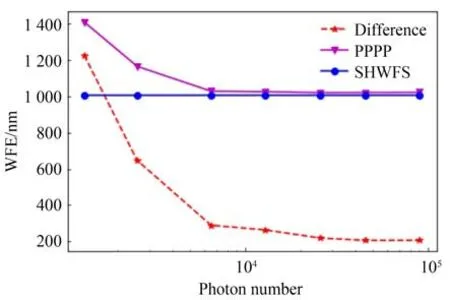
图12 不同光子数下的测量结果Fig.12 Reconstruction results with different photon numbers

现在将SLM 从位置1 移动到位置2，用以模拟上行激光和后向散射成像均存在大气湍流的情况。在这种情况下，光通过SLM 两次，造成约87%的光损失，因此，BS2和BS3被暂时移除以确保有足够的光进入PPPP 路径。当SLM 位于位置2 时，PPPP 重 构结果如 图13 所示。由图13 可以看出，当SLM 加载第4，6，12，14 等几项Zernike 模式时，“difference”约为“position 2”数值的五分之一，误差较小；但在第5，11 项Zernike 模式时，“difference”约为“position 2”数值的二分之一，误差较大。将SLM 从位置1 移到位置2，理论上唯一的区别是后向散射光斑成像时会受到SLM（即大气湍流）的影响，其影响是使后向散射光斑变模糊，其模糊程度取决于大气湍流的强度。理论上，对后向散射光斑的采样数与传统的夏克-哈特曼波前探测器子孔径数相对应，因此，对后向散射光斑成像时不需要很高的分辨率，或者说可以采用像素尺寸较大、像素数较少的探测器来成像。这种情况下，大气和望远镜系统的PSF 会限制在较少的几个（甚至1 个）像素内，此时，大气湍流对后向散射光斑成像的影响就变得微乎其微。通过仿真发现［19］，如果采用38×38 个像素来对h1和h2的后向散射光斑进行成像，大气湍流（r0=0.1 m）引起的PSF 会限制在1 个像素内，此时，大气湍流对后向散射光斑成像的影响就可以忽略不计。但是在实验中，SLM 置于位置1 和位置2 对波前测量结果有一定影响（图13），这可能是由于实验中无法保证当SLM 位于位置1 和位置2 时，光斑经过SLM 的同一区域，而SLM 衍射效应较强，微小的位置偏差就会导致一定的测量误差。

图13 空间光调制器位于位置1 和位置2 时重构结果对比Fig.13 Comparison of PPPP reconstruction results with SLM at positions 1 and 2

除了SLM，实验还采用另一种波前畸变模拟器件，即简易的透明塑料片，放置于位置2，对应的光斑分布和重构相位如图14 所示。图14（a）和14（b）为未加透明塑料片时h1和h2对应的光强分布I10和I20，I0为两者的平均值。为了去除光学系统本身的静态像差，需要进行校准，即将添加透明塑料片后测量得到的光强与未加透明塑料片的光强I10和I20相减（图14（d）和14（e）），得到实际用来重构的光强差信号，如图14（f）所示。图14（g），14（h）为PPPP 和SHWFS得到的重构相位，其中PPPP 重构相位的RMS 为1 370.72 nm，SHWFS 重构相位的RMS 为1 356.60 nm，它们差值的RMS 为414.80 nm，约为初始相位的30%。

图14 透明塑料片实验结果Fig.14 Measurements with transparent plastic sheet

为了验证重复性，利用不同的透明塑料片产生6 种不同的波前畸变，其PPPP 和SHWFS 的重构结果如图15 所示。可以看出，对于透明塑料片产生的6 种不同的畸变，PPPP 和SHWFS 重构相位的差异大约为初始相位的30%，与SLM 结果类似。

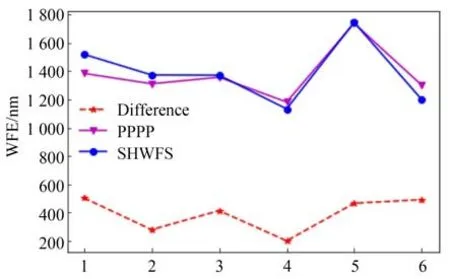
图15 透明塑料片产生的6 种不同畸变的测量结果Fig.15 Reconstruction results with 6 different phase aberrations generated by transparent plastic sheets

5 结论

本文通过实验验证了一种新型的波前探测技术PPPP，并根据光强传输公式，采用两个不同传输距离的光强分布演变来实现波前畸变的探测。由于PPPP 采用上行通信激光本身的后向瑞利散射，所测量的大气湍流方向与通信卫星方向一致，因此，可以有效解决星地激光通信中的提前角问题。根据PPPP 测量原理，实验包含3 个主要环节：上行激光束在大气湍流中的传播，对上行激光的两个不同高度的瑞利后向散射光斑的成像，以及利用Zernike 模式法进行相位重构。实验模拟1 m 口径地基望远镜，两个传输高度分别为10 km 和17 km，采用空间光调制器和透明塑料片作为两组畸变模拟器件。实验结果表明，PPPP 和通用的夏克哈特曼波前探测器得到了相似的重构相位，两者的差异约为初始相位的30%。如果进一步扩大地面望远镜的口径，可以有效降低PPPP 的非线性效应，从而提高其波前探测的准确性。